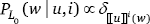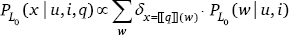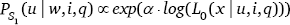1 Introduction
How should we characterize the meaning of sentences, and how do we (as speakers) learn that meaning? These questions call into focus the intersection of two traditions of inquiry: the semantics of natural language and language development. One of the key empirical methodologies for questions at this intersection is the truth-value judgment task (Crain & McKee 1985; Crain & Thornton 1998). Here, we use a complementary methodology to investigate how to interpret truth-value judgment behavior in specific cases where the truth-value judgment task has been used. More specifically, we model the cognitive processes, both linguistic and extra-linguistic, that deliver truth-value judgment task behavior in precise experimental contexts. This computational cognitive modeling allows us to separate out the contributions from these different cognitive processes, in contrast with behavioral contexts where these processes interact.
1.1 Truth-value judgments for assessing meaning
Knowing the meaning of some sentence S means knowing the conditions required for S to be true—the truth conditions of S. A sentence’s truth conditions might not exhaust the meaning of that sentence; they eschew connotative and social elements of meaning. Still, semanticists agree that truth conditions are a key component of sentence meaning: if you know what a sentence means, then you can identify the sorts of situations it describes. Therefore, one way of diagnosing sentence meaning is to map out the situations a sentence can describe (i.e., those situations in which the sentence is true) and those it cannot. In other words, one way of diagnosing sentence meaning is to consult one’s truth-value judgments for a range of situations. Those situations where the sentence is judged as a true description are then compatible with the sentence’s meaning. Semanticists are constantly engaged in investigations of this sort: imagine a situation and evaluate whether a sentence of interest is true in that situation. However, individuals without this sophisticated linguistic training—naive adults and children—often need to be helped with (i.e., tricked into) this reasoning. Enter the truth-value judgment task.
Rather than asking someone to imagine situations and the sentences that describe them, truth-value judgment tasks provide this information explicitly. In particular, to successfully engage children in the necessary reasoning, child truth-value judgment tasks often involve fairly elaborate setups that try to imitate natural conversational contexts. The hope is that more natural conversational contexts will mitigate any unusual pragmatics that would interfere with children’s reasoning (Crain & McKee 1985; Crain & Thornton 1998).
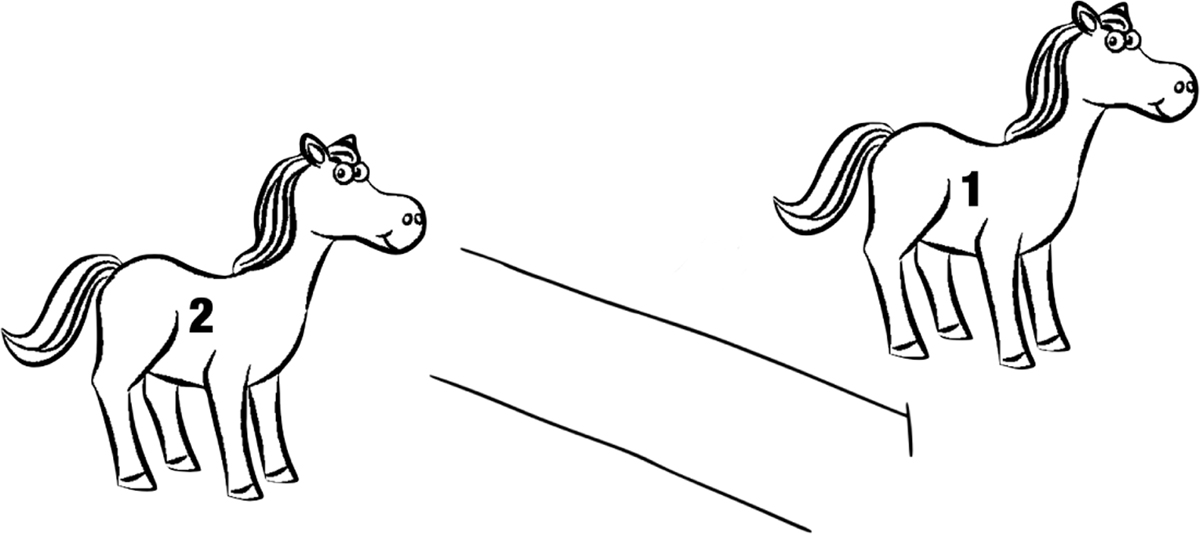
In a typical child truth-value judgment task implementation, a story is acted out using figures and props (e.g., a story about horses jumping over things like logs and fences). At the end of the story, an observer (often a puppet so the child won’t be intimidated) describes the outcome of the story with a statement (e.g., None of the horses jumped over the fence). This statement is the test sentence, and the child is meant to evaluate that sentence against the story scenario. The child then is asked to decide whether what the observer (puppet) said was okay (i.e., “yes” or “no”)—that is, whether the child would endorse the puppet’s statement as a reasonable thing to say, given the story scenario. A puppet is used, rather than an adult experimenter, because children are less hesitant to disagree with a puppet who they think said something wrong than with an adult who they think said something wrong (Crain & McKee 1985; Crain & Thornton 1998).
The tacit linking hypothesis assumes that when children endorse the observer’s description, they judge the sentence as true in the story scenario; when they choose not to endorse the description, they judge it as false. Typically, a child’s response (i.e., endorsing with “yes” or not endorsing with “no”) is followed up with an explicit question about why the child answered the way she did—this questioning also helps to ensure that the child is saying “yes” or “no” because the child thinks the observer’s description is appropriate or not, respectively.
We reiterate that all these accommodations in the truth-value judgment task aim to mitigate any unusual pragmatics that children might bring to the experimental scenario, given that this task is still a rather unnatural conversational situation. In particular, the truth-value judgment task does not ask children to simply interpret an utterance (as they would do in a natural conversation), by inferring the state of the world that the speaker is describing. Instead, in the truth-value judgment task, the state of the world is already known by both the child participant and the observer who produces the utterance; so, the child’s task is not to infer the state of the world, but rather to decide whether the observer’s utterance aptly describes that state of the world. A simple way for children to make this judgment is to decide if they themselves would produce it, given the observed state—an odd kind of production task (Degen & Goodman 2014). The reasoning involved is fairly sophisticated, so child implementations of the truth-value judgment task are constantly being improved to facilitate children’s ability to successfully perform this reasoning and demonstrate their underlying linguistic knowledge (Thornton 2017).
A truth-value judgment task can of course also be used for adult participants. The special design of child truth-value judgment tasks is meant to facilitate reasoning about the truth-value of specific statements. So, adults can benefit from the same truth-value judgment design features (though adults may lose patience with the more child-like aspects, such as listening to a puppet).
1.2 A concrete truth-value judgment task example: Quantifier scope ambiguity
At this point, it will be useful to consider a concrete example and the motivating case study for our investigation of truth-value judgments: universally-quantified sentences with negation, such as Every horse didn’t jump over the fence. Such sentences are interesting from a theoretical perspective because they typically allow ambiguity (at least in English), with different interpretations conditioned by the scope of the logical operators introduced by every and negation. Such a sentence allows two interpretations (shown in (1)). Under the surface interpretation, the logical scope of the operators corresponds to their scope at surface structure (every over n’t: ∀ > ¬); under the inverse interpretation, the logical scope inverts the surface scope (n’t over every: ¬ > ∀). Each scope option therefore leads to a different interpretation: surface scope corresponds to a “none” interpretation while inverse scope corresponds to a “not all” interpretation.
| (1) | Every horse didn’t jump over the fence. | |
| a. | Surface scope (∀ > ¬): | |
| None of the horses jumped over the fence. | ||
| b. | Inverse scope (¬ > ∀): | |
| Not all of the horses jumped over the fence. | ||
Truth-value judgment data have demonstrated differences between adults and children when it comes to their judgments of sentences like (1) in certain story scenarios. To appreciate these differences, consider the story scenario in Figure 1: there are two horses, and one jumped over the fence while the other did not. So, the surface interpretation of (1) is false: it is false that none of the horses jumped over (because horse 1 did in fact jump over). However, the inverse interpretation is true: it is true that not all of the horses jumped over (horse 2 didn’t).
In a not-all scenario of this sort, adults readily endorse statement (1) (90–100% acceptance) while five-year-old children typically do not (10–20% acceptance; e.g., Musolino 1998; 2006; Viau et al. 2010). Following the implicit linking hypothesis mentioned above for the truth-value judgment task, these child judgments have been interpreted to mean that children struggle to access the inverse interpretation of sentences like (1) the way that adults can. The interesting question is why (and perhaps even whether) children struggle to access that interpretation, and there are several possibilities that have been discussed in the literature cited above. Perhaps children are unable to generate the inverse interpretation at all because their semantic knowledge is still developing (a grammatical factor). Perhaps children can generate the inverse interpretation, but not access it in the truth-value judgment task because of their developing processing abilities (a grammatical factor). Perhaps children can in fact generate and access the inverse interpretation, but choose not to endorse the test sentence for other—typically pragmatic—reasons (e.g., children don’t believe the sentence is a reasonable thing to say, given the story scenario); this resistance to endorsement would be due to one or more pragmatic factors.
Interestingly, strategic changes to the truth-value judgment task setup lead to more adult-like behavior, such that children more readily endorse sentences like (1) in a not-all scenario as in Figure 1. However, despite the carefully-designed manipulations of the experimenters, it often remains unclear which factors are responsible for children’s differing behavior: grammatical factors, pragmatic factors, or both. Here is where computational cognitive modeling can help us.
1.3 Computational cognitive modeling of the truth-value judgment task
Computational cognitive models implement cognitive theories concretely. In particular, a computational cognitive model articulates a hypothesis of how different components of underlying knowledge interact to produce observable behavior (e.g., Goodman & Frank 2016; Pearl 2017; in press; Scontras et al. electronic). Here, we use computational cognitive modeling to implement cognitive theories of ambiguity resolution in context, specifically how a participant (child or adult) would resolve a quantifier scope ambiguity like (1) in story contexts like Figure 1. By articulating how different cognitive components interact—both grammatical and pragmatic components—a computational cognitive model can predict not only which factors contribute to the observed truth-value judgment endorsement behavior, but also how much each factor contributes. Doing so allows us to transparently untangle the separate contributions of each factor.
So, by applying a modeling approach to the question of truth-value judgments for scopally-ambiguous utterances, we can identify which cognitive factors lead to adult-like judgments and how they do so. We can then see if these same factors can lead to child-like judgments, and, if so, how they do so. When we have potential explanations for both adult behavior and child behavior, we can then articulate a developmental theory: what needs to change for children to become adult-like. More generally, when we understand how the underlying cognitive factors can yield observable endorsement behavior in the truth-value judgment task, we better understand the truth-value judgment task itself, and how to interpret truth-value judgment results.
An additional benefit of computational cognitive models that predict observable behavior (such as the endorsement behavior in a truth-value judgment task) is that model predictions can then be tested by further behavioral work. If we find that the modeling predictions match what humans do (e.g., endorsement rates for other contexts and/or test sentences), we have strong support for the model-implemented theory of how the underlying components interact.
1.4 The rest of this paper
This paper is structured as follows. We begin with an overview of the empirical facts concerning children’s ambiguity-resolution behavior in truth-value judgment tasks, together with the relevant task manipulations that make children more adult-like. We then present our computational cognitive model of utterance endorsement in the truth-value judgment task, which is conceived within the Bayesian Rational Speech Act modeling framework (Goodman & Frank 2016; Scontras et al. electronic). With this modeling approach, we demonstrate how both child and adult truth-value judgment endorsement behavior could be captured using a single model with different parameter settings. In other words, we show how the same cognitive factors can interact in the same way to produce either child-like or adult-like behavior. The differences are quantitative in nature, such that different values for the same factor yield diverging behavior. So, our model predicts that adults and children are in fact performing a qualitatively similar pragmatic calculus when evaluating ambiguous utterances in the truth-value judgment task.
Given this finding, our model predicts that adults should be affected by the same sorts of task manipulations that have been found to modulate children’s behavior. We explore this prediction, considering truth-value judgment data for a case of ambiguity that leaves adults looking like children. We demonstrate how our model can be extended to capture this adult truth-value judgment task behavior, underscoring how the same underlying cognitive variables interacting in the model-specified way can account for a variety of truth-value judgment task data.
More generally, our findings suggest that child and adult truth-value judgment behaviors could be driven by the same underlying cognitive factors. This observation raises the possibility that the only difference between children and adults is different values for those factors. In other words, to become adult-like, children would need to adjust these values to be adult-like values; however, they would not need to qualitatively change how they resolve scope ambiguity. This finding would therefore support continuity in the development of scope ambiguity resolution from childhood into adulthood. We conclude by synthesizing our findings and discussing their implications for our understanding of language development, methods that can be fruitfully used to assess that development, and the generalizability of this model of ambiguity resolution beyond the specific cases considered here.
2 Children on the truth-value judgment task
Children’s behavior with scopally-ambiguous utterances in the truth-value judgment task has been shown to be sensitive to manipulations of the experimental context. In the basic task, children are presented with a background story about the agents—for example, horses engaging in some activities. After this background story, children watch as the agents attempt to complete an action, such as jump over a fence. The critical not-all result state meant to prompt the inverse scope interpretation is illustrated in Figure 1, where horse 1 jumps over the fence and horse 2 does not. In this scenario, the surface interpretation of the sentence in (1) is false (again, because horse 1 did jump; therefore, none jumped is false), and the inverse scope interpretation is true (again, because horse 2 did not jump; therefore not all jumped is true).
A puppet then produces an utterance, such as the sentence in (1), and the child is asked to state if the puppet is right.1 That is, the child is asked whether she would endorse the puppet’s utterance as a true description of the scenario. Typically, children refuse to endorse the puppet’s utterance in inverse-verifying scenarios like Figure 1, saying that the puppet is wrong; in contrast, adults readily endorse the utterance in this context. This behavior has been interpreted as children failing to access the inverse scope interpretation that would make the utterance true. That is, if children could access the inverse scope interpretation, they would recognize that not all of the horses jumped over the fence is true in this scenario, and therefore they should endorse the scopally-ambiguous utterance in (1). But given that children typically do not endorse the utterance in this scenario, children’s behavior is interpreted as evidence that they must not access the inverse scope interpretation.
Previous accounts of children’s scope-interpretation behavior have recognized that both processing and pragmatic factors may contribute to non-adult-like behavior. Musolino (1998; 2006) observed that the surface scope interpretation in (1a) may be easier to process because the scope relationship at logical form (i.e., ∀ > ¬) aligns with the linear order of these elements in the utterance (i.e., Every precedes n’t). In contrast, for the inverse scope interpretation in (1b), this parallelism does not hold, with the scope relationship (i.e., ¬ scopes over ∀) opposite the linear order of the elements in the utterance. Musolino hypothesized that this lack of parallelism would make the inverse scope interpretation more difficult to access. In line with this prediction, Conroy et al. (2008) used a sentence-completion task to show that, when adults are time-restricted, they favor the surface scope interpretation (i.e., 80% surface scope when time-restricted vs. 50% when unrestricted). We thus see a potential role for processing factors in children’s inability to access the inverse scope. Perhaps children, with their still-developing processing abilities, are unable to allocate sufficient processing resources to reliably access the inverse scope interpretation.
In addition to this processing factor, Gualmini et al. (2008) noted that discourse properties, such as what children consider to be the question under discussion (QUD), may impact their scope-interpretation behavior. Formal theories of pragmatics suggest that all discourse transpires with respect to some QUD, whether implicit or explicit; utterances in the discourse need to (at least partially) answer the QUD to be pragmatically felicitous (Roberts 2012). Gualmini et al. (2008) suggest that children are very sensitive to this requirement. In particular, children may be able to access the inverse scope interpretation but nonetheless choose the surface scope interpretation because it better answers the perceived QUD in the contrived experimental setups. So, children’s observed behavior would derive from a still-developing ability to manage the contextual information available and correctly infer the intended QUD.
Interestingly, various alterations to the truth-value judgment task setup have yielded more adult-like behavior in children—namely, greater rates of endorsing the puppet’s ambiguous utterance in not-all scenarios. For example, Musolino & Lidz (2006) hypothesized that negation in an utterance might require certain felicity conditions to be met. In particular, negated utterances require a preceding affirmative context with which to contrast (Wason 1965). Musolino & Lidz augmented the basic truth-value judgment task to include an additional contrast condition in which the puppet precedes its negative scopally-ambiguous utterance with a contrasting affirmative clause. This additional clause describes a previous successful story action (an “early success”), as in Every horse jumped over the log, but every horse didn’t jump over the fence. This early-success contrast manipulation increased children’s willingness to accept the scopally-ambiguous utterance in the not-all scenario: children in the baseline condition endorsed the puppet’s statement just 15% of the time, while children in the early-success condition endorsed the puppet’s statement 60% of the time (N = 20). Viau et al. (2010) replicated this increase in utterance endorsement (∼60%) using only an early-success story context (N = 24). That is, the higher utterance endorsement rate was maintained by an early-success story context alone; children did not need an explicit-contrast clause in the test utterance (instead hearing only a scopally-ambiguous utterance like Every horse didn’t jump over the fence, just as in the original experiments by Musolino & Lidz).
Notably, the early-success affirmative-context manipulation potentially changes several aspects of the experimental context. First, observing early successes can shift participants’ expectations about successful outcomes more generally in the experimental world. This shift then potentially increases the salience of a QUD targeting this success, such as did all the horses succeed? (all?). Recognizing this QUD’s potential significance, Gualmini (2004) attempted to manipulate the experimental context so it favored the all? QUD. With all? as the salient QUD, children’s endorsement of a scopally-ambiguous utterance that perfectly answered all? in the critical not-all scenario increased to 90%. Even for a scopally-ambiguous utterance that does not fully answer the all? QUD, children’s endorsement rate was at 50% with the all? QUD—markedly higher than the 15% baseline from the original study by Musolino & Lidz (2006). This finding highlights that privileging the all? QUD increases children’s utterance endorsement in these scenarios.
In addition to altering expectations about likely states of the world and QUDs, a third potential impact of the early-success affirmative-context manipulation involves scope access. By altering the experimental world expectations and/or expectations about the QUD to increase access to the inverse scope, the inverse scope interpretation may remain more accessible for later use. Viau et al. (2010) term this prolonged increase in accessibility “structural priming”. Children who are better able to access the inverse scope are then more likely to endorse the scopally-ambiguous utterance in subsequent not-all scenarios. Viau et al. investigated structural priming explicitly by attempting to directly alter the accessibility of the inverse scope interpretation. In one modified truth-value judgment task, the authors attempted to prime the access of the inverse scope interpretation; in another modified task, they attempted to directly prime the inverse scope’s logical structure (e.g., ¬ > ∀).
The first structural priming manipulation was implemented via the now-familiar early-success affirmative-context manipulation. For the first three trials, the prior experimental context indicated successful outcomes; the effect was that children endorsed the scopally-ambiguous utterance 50% of the time. Crucially, the subsequent three trials removed the supportive affirmative-context manipulation, yet children continued to not only endorse the scopally-ambiguous utterance, but to endorse it more than they had before (80% endorsement). Viau et al. (2010) attribute this result to a priming effect of the inverse interpretation from the first three trials: having accessed the inverse structure in the early trials, children are more likely to access that same structure in later trials. However, the increase in utterance endorsement could be due to the privileging of multiple factors that are products of the affirmative-context manipulation: (i) expectations about successful outcomes in the experimental world, (ii) the salience of the all? QUD, or (iii) the ease of access to the inverse scope interpretation.
The second structural priming manipulation removed the affirmative-context story in the first three trials. In its place, children were asked whether they would endorse a scopally-unambiguous utterance (e.g., not every horse jumped over the fence), whose interpretation had logical operators in the same configuration as the inverse scope interpretation of the scopally-ambiguous utterance (i.e., ¬ > ∀). Children endorsed this utterance 80% of the time. In the subsequent three trials, children were asked if they would endorse the scopally-ambiguous utterance in the same experimental scenario—and their endorsement rate remained at 80%. Viau et al. (2010) interpret this effect as priming of the relevant logical form: the inverse scope was easier to access in the scopally-ambiguous utterance because it was recently accessed in the unambiguous utterances. The authors argue that this priming effect proceeded in the absence of manipulations to the pragmatic context; yet, even here there may still be pragmatic factors at work. The unambiguous utterance accomplishes three things: (i) it provides an instance of the ¬ > ∀ configuration, (ii) it provides information about successful outcomes, and (iii) it suggests the all? QUD, answering it with no. Thus, in this attempt to prime the inverse logical form, the authors may have also altered expectations about the pragmatic context of the experiment as it relates to successful outcomes and relevant QUDs.
These experimental studies highlight at least three core factors (two pragmatic, one grammatical processing) that underlie children’s utterance endorsement behavior in the truth-value judgment task: (i) pragmatic: expectations about the experimental world (e.g., how likely successful outcomes are), (ii) pragmatic: expectations about the QUD (e.g., if it is relevant to establish whether all outcomes were successful), and (iii) grammatical processing: the accessibility of the inverse scope (i.e., the ease by which the logical form is accessed). These experimental studies have also supported different theoretical proposals for the source of children’s differences. The proposals split on whether they attribute the differences solely to an inability to manage contextual information (i.e., pragmatic factors; Gualmini 2008) or whether grammatical processing deficits also significantly contribute (i.e., difficulty accessing inverse scope; Viau et al. 2010). Importantly, it is not obvious from any of the existing experimental manipulations how to separate the independent contributions of these components. In an attempt to capture and independently manipulate the contributions of each of the pragmatic and grammatical processing factors, we formalize their role in the interpretation of scopally-ambiguous utterances, using tools from computational cognitive modeling.
3 A computational cognitive model for every-not utterances
We model ambiguity resolution within the Bayesian Rational Speech Act (RSA) modeling framework (Goodman & Frank 2016), which views language understanding as a social reasoning process. The RSA framework finds broad empirical support from its ability to successfully model a range of pragmatic language phenomena, from scalar implicature (Goodman & Stuhlmüller 2013) and vague gradable adjectives (Lassiter & Goodman 2013) to generic utterances (Tessler & Goodman 2019) and hyperbole (Kao et al. 2014b). Within the framework, language understanding is modeled by a pragmatic listener L1 who interprets an utterance by reasoning about a cooperative speaker S1 who is trying to inform a hypothetical literal listener L0 about the world. We build on this framework assumption for our own RSA model implementation, described in more detail below. We note that the Bayesian inference mechanism on which this modeling framework relies is plausible for young children to use; a body of developmental evidence suggests that even very young children are capable of this kind of inference (3 years: Xu & Tenenbaum 2007; 9 months: Gerken 2006; 6 months: Denison et al. 2011; among many others).
Our model is a “lifted-variable” extension, in which the ambiguous utterance’s literal semantics is parameterized by interpretation-fixing variables (e.g., whether the scope is surface or inverse). Hearing an ambiguous utterance, a pragmatic listener reasons jointly about the true state of the world (e.g., how many horses jumped over the fence), the scope interpretation that the speaker had in mind (i.e., surface vs. inverse), as well as the likely QUD that the utterance addresses (e.g., how-many? vs. all?).
To connect our model’s predictions with the available truth-value judgment data in the descriptive truth-value judgment tasks described above, we follow recent suggestions in the literature for how to treat truth-value judgments. In particular, truth-value judgments are not viewed as pure language comprehension behavior, but rather as a form of language production (e.g., Degen & Goodman 2014; Jasbi et al. 2019). Recall from our discussion of the task above that it does not present as a typical comprehension task because both the participant and the speaker in the particular truth-value judgment tasks we model are already aware of the true world state. So, the participant is not trying to simply comprehend the utterance, which would involve the participant trying to infer the world state, given the utterance. Instead, participants in the truth-value judgment task are shown a scenario and asked if a specific utterance can accurately describe that scenario. In this way, the truth-value judgment task seems to be asking if a speaker should describe the given scenario with the test sentence.
A simple way for participants to make this decision is to decide if they would produce that utterance, given that scenario. If so, participants should endorse the utterance; if not, participants should not endorse the utterance. So, if participants judge the utterance as a reasonable description because they judge that they themselves could produce that utterance in the scenario, the participants endorse the utterance in the truth-value judgment task. As noted before, this setup means that participants have to effectively reason about their own potential production. Given this understanding of the task, we model participants’ truth-value judgment behavior as the (relative) endorsement of a pragmatic speaker S2 for an utterance about an observed situation; S2 makes this decision by reasoning about the probability that L1 (who is reasoning about S1’s reasoning about L0) would arrive at the correct world state after hearing the utterance. Given that language understanding and language production are modeled as cases of recursive social reasoning between speakers and listeners, there is no production behavior without reasoning about comprehension (i.e., reasoning about how a listener would interpret the utterance), and there is no comprehension behavior without reasoning about production (i.e., reasoning about how a speaker would have chosen the utterance); in this way, the model intentionally blurs the boundaries of production vs. comprehension.
To connect the model’s pragmatic speaker predictions to available truth-value judgment task data, we follow most RSA implementations and assume that the model is a population-level model of the relevant phenomenon. In our case, this assumption means that a predicted endorsement probability from pragmatic speaker S2 maps to an average participant endorsement rate in a particular experimental setup. That is, averaging across participants in a particular experimental setup yields some endorsement rate re (e.g., re = 80%), which is compared against the model’s predicted probability of endorsement pe (e.g., pe = 0.80).2
3.1 Model specification
We take world states w ∈ W to correspond to the number of successful outcomes, for example, the horses that successfully jumped over the fence (W = {0,1,2}); the world success base rate bsuc determines the probability that any individual will succeed.3 We assume a simple truth-functional semantics where an utterance u denotes a mapping from world states to truth values (Bool = {true, false}). We parameterize this truth function so that it depends on the scope interpretation i ∈ I = {inverse, surface}, ⟦u⟧i: W → Bool.
We consider two alternative utterances u ∈ U: the null utterance (i.e., saying nothing at all, and so choosing not to endorse the utterance) and the scopally-ambiguous utterance amb (e.g., Every horse didn’t jump over the fence); U = {null, amb}. We include no additional alternative utterances because participants are given none when asked to provide truth-value judgments: they can either choose to endorse the ambiguous utterance (i.e., choose to produce it as a description of the scenario) or they can choose to not endorse the utterance. In the latter case of not endorsing the target utterance, we model this choice as the participant deciding that it would be better to communicate no information with their utterance, rather than the (misleading) information conveyed by the target utterance. To communicate no information, the model provides a null tautology, which tells the listener nothing new and leads instead to the listener relying on prior knowledge.
The utterance semantics appears in (2),4 where the interpretation parameterization only impacts the truth value for utterance amb (since only amb has multiple interpretations available). If inverse is active, amb receives a “not-all” reading and is true so long as not all (two) outcomes were successful (i.e., w ≠ 2). If surface is active, amb receives a “none” reading, which is true only in a world with zero successes (i.e., w = 0).
| (2) | Utterance semantics ⟦u⟧i: | |
| a. | ⟦null⟧i = λw. true | |
| b. | ⟦amb⟧i = if i = inverse, then ⟦inverse⟧, else ⟦surface⟧ | |
| where: ⟦inverse⟧ = λw. w ≠ 2 | ||
| ⟦surface⟧ = λw. w = 0 | ||
The literal listener L0 hears some utterance u (e.g., Every horse didn’t jump over the fence) with intended interpretation i (e.g., inverse)5 and returns a uniform distribution over those world states w that are compatible with the literal semantics of u (e.g., w ∈ {0,1}, so the normalized p(w = 0) = p(w = 1) = 0.5).6 The function maps a Boolean truth value to a probability, 1 or 0 (e.g., true maps to 1). So, for instance, for the inverse interpretation where the interpretation is true for w = 0 or 1 and false for w = 2, = 1, while .
We consider three QUDs q ∈ Q: (i) “How many horses succeeded?” (how-many?), (ii) “Did all of the horses succeed?” (all?), and (iii) “Did none of the horses succeed?” (none?). The QUDs serve as projections from the inferred world state to the relevant dimension of meaning, q: W → X (Kao & Wu & Bergen & Goodman 2014b; Kao & Bergen & Goodman 2014a). In practice, the QUDs establish partitions on the possible world states, as shown in (3): how-many? is an identity function on world states, all? returns true only if both outcomes were successful, and none? returns true only if none of the outcomes were successful. As shown here, different QUDs may partition world states in different ways: how-many? has as many partitions as there are worlds (here, three: w = 0 in one, w = 1 in the second, w = 2 in the third); all? and none? have only two partitions, but distribute the worlds differently across those two partitions (all? has w = 0 and w = 1 in one partition and w = 2 in the other; none? has w = 0 in one partition and w = 1 and w = 2 in the other).
| (3) | QUD semantics ⟦q⟧: | |
| a. | ⟦how-many?⟧ = λw. w | |
| b. | ⟦all?⟧ = λw. w = 2 | |
| c. | ⟦none?⟧ = λw. w = 0 | |
To capture the notion that communication proceeds relative to a specific QUD q, L0 must infer not only the true world state w, but also the value of the QUD applied to that world state, ⟦q⟧(w) = x ∈ X. When q is how-many?, X ranges over W; otherwise, X ranges over Bool. In other words, when q is how-many?, L0 infers whether x is 0, 1, or 2; when q is all?, L0 infers whether x is true (i.e., w ∈ {2}) or false (i.e., w ∈ {0, 1}); when q is none?, L0 infers whether x is true (i.e., w ∈ {0}) or false (i.e., w ∈ {1, 2}).7
The speaker S1 chooses an utterance u in proportion to its utility. Utterance utility concerns the chance of successfully communicating q’s answer (i.e., the answer to the QUD) to L0. Thus, S1 chooses utterances by maximizing the probability that L0 arrives at the intended x from u. This selection is implemented via a softmax function (exp) and free temperature parameter α, which controls how “rational” or “greedy” the speaker will be in utterance selection; as α increases, S1 is more likely to choose utterances with higher utility. One way to think about α is as a contrast parameter that controls how the modeled speaker views relative probabilities in a probability distribution. When α = 1, the modeled speaker views the true relative probabilities (e.g., 0.6 vs. 0.4 utility); when α < 1, the contrast is decreased, and so the differences between relative probabilities are smoothed away (e.g., 0.55 vs. 0.45 utility); when α > 1, the contrast is increased, and so the differences between relative probabilities are sharpened (e.g., 0.7 vs. 0.3 utility). In this way, α > 1 leads S1 to choose utterances with higher utility more often—the relative probability of a higher utility utterance is increased (e.g., from 0.6 to 0.7).8
Utterance interpretation happens at the level of the pragmatic listener L1, who interprets an utterance u to jointly infer the world state w, the interpretation i, and the QUD q. We therefore model ambiguity resolution as pragmatic inference over an under-specified utterance semantics (i.e., the interpretation variable i; Scontras & Goodman 2017). To perform this inference, L1 inverts the S1 model by Bayes’ rule, and so the joint probability of w, i, and q is proportional to the likelihood of S1 producing utterance u given world state w, interpretation i, and QUD q, as well as the priors on w, i, and q.
Importantly, it is only at the level of the pragmatic listener L1 that a human listener is plausibly modeled; the other levels encode what this pragmatic listener is imagining about a hypothetical speaker S1, who in turn is imagining a hypothetical naive listener L0. So, as part of this reasoning process, L1 considers how S1 and L0 would reason under certain conditions (i.e., if certain things were true). Assuming that S1 and L0 know a number of things that the pragmatic listener L1 actively infers features prominently in prior RSA modeling studies (Scontras et al. electronic).
To model the utterance endorsement implicit in truth-value judgment behavior, we need one more level of inference. As mentioned above, we follow Degen & Goodman (2014) and Jasbi et al. (2019) in modeling descriptive truth-value judgment data as speaker production behavior, which means we need to generate predictions from a speaker layer in our model. However, S1 is not a reasonable model of a human speaker in the task because S1 jointly observes the world state, the intended scope interpretation, and the intended QUD; human participants observe only the world state (e.g., the number of horses who jumped). We therefore require an additional speaker layer to model human production behavior in the task. The pragmatic speaker S2 observes only the true world state w and selects u by inverting the L1 model; thus, S2 maximizes the probability that a pragmatic listener would arrive at w from u by summing over possible interpretations i and QUDs q that accompany world w. In other words, S2 chooses u to communicate w by simulating how L1 would resolve i and q for each of the possible utterances.
3.2 Model predictions
To generate model predictions, we must fix various model parameters. The S1 speaker rationality parameter α > 0 is set to 1 (i.e., no scaling of S1’s utility), although we find the same qualitative patterns with higher values of α. The priors P(w) and P(q) correspond to expectations for the discourse context (i.e., likely world states or QUDs). In particular, more extreme priors (i.e., probabilities closer to 0 or 1) indicate more categorical beliefs about the discourse context; more uniform priors indicate less categorical beliefs. In the default case, we set these priors so that the individual success base rate bsuc is set to 0.5 (i.e., horses have a 50% chance of success) and the relevant QUDs have equal probability (i.e., P(how-many?) = P(all?) = P(none?) = ⅓). The interpretation prior P(i) corresponds to how easy it is to access the inverse scope interpretation. This prior aggregates the various factors that affect accessibility of the inverse scope (e.g., constructing the semantic representations, cognitive processing factors like memory and attention) into a single variable; priors near 0 indicate that the inverse scope is very hard to access relative to the surface scope, while priors near 1 indicate that the inverse scope is very easy to access. In the default case, P(inverse) = P(surface) = 0.5. Because model priors correspond to the beliefs that conversational participants bring to bear on the communication scenario instantiated by a truth-value judgement task, these default settings model a case where a conversational participant has maximal uncertainty about the relevant parameter values.
To better understand children’s utterance endorsement behavior with scopally-ambiguous utterances, we can independently manipulate the values of the priors on W, Q, and I—modeling the possibility that different participants would enter the communication scenario with different beliefs—and observe their impact on utterance endorsement in not-all scenarios. That is, we can systematically manipulate the relevant priors to test how pragmatic factors (W and Q) and processing factors (I) contribute to adult-like vs. non-adult-like utterance endorsement behavior in the truth-value judgment task. Our modeling target is the behavioral pattern where children—unlike adults—generally do not endorse every-not utterances in the absence of a supportive pragmatic context (as implemented by the various manipulations to the basic task design). Concretely, our modeling target is low (e.g., 15%) vs. high (e.g., 60–100%) utterance endorsement; via this model, we conduct an analytic exploration of plausible factors that could lead to both observed behaviors.
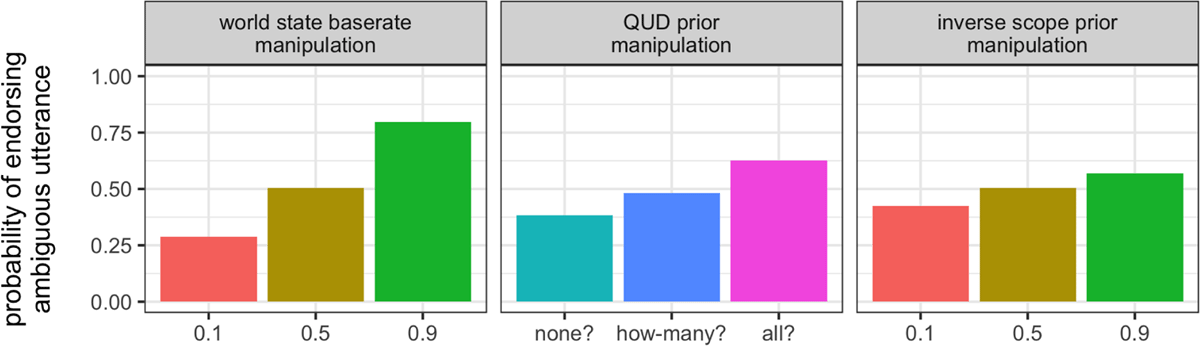
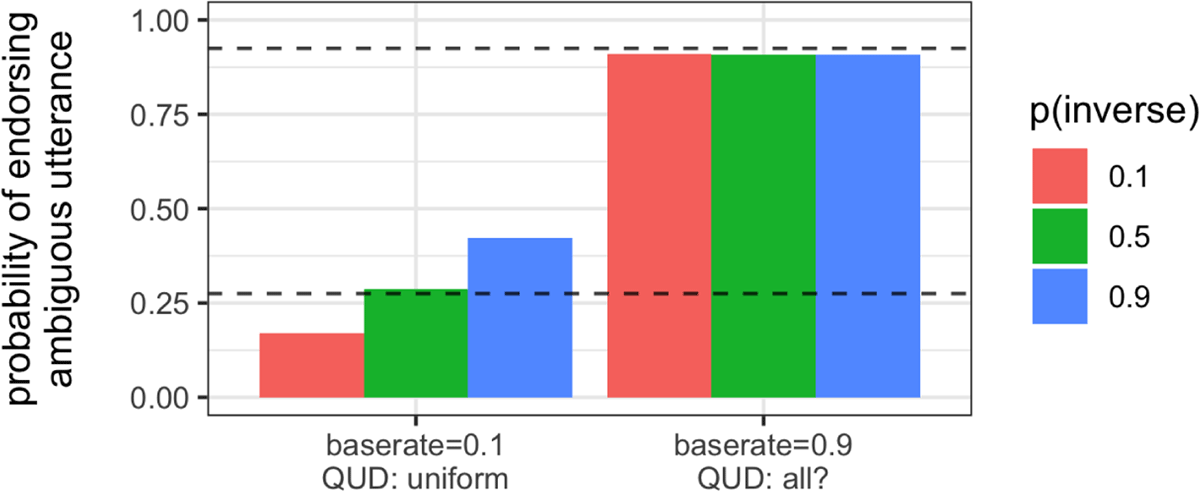
To investigate the effect of manipulating the world state prior (Figure 2, left panel), we systematically alter the success base rate bsuc; in the horse context, bsuc controls beliefs about how likely horses are to succeed at jumping. Holding the QUD and scope priors at their default values, we see a marked increase in endorsement of the ambiguous utterance in the not-all scenario as beliefs about horse success increase. Utterance endorsement is at its lowest (0.29) when prior knowledge suggests that horses are particularly unlikely to succeed at jumping (i.e., that bsuc is 0.1); utterance endorsement is at its highest (0.80) when we believe horses are very likely to succeed (i.e., that bsuc is 0.9).
Model predictions for ambiguous utterance endorsement (e.g., Every horse didn’t jump over the fence) in a not-all scenario (e.g., 1-of-2 horses jump over the fence). Lower endorsement probability corresponds to less adult-like (i.e., more child-like) behavior. For the QUD factor, the favored parameter value receives most of the prior probability weight (P(favored) = 0.9). For the processing variable (scope), the prior corresponds to how strongly the inverse scope is favored.
Just as with the world state prior, we can systematically manipulate the QUD prior (Figure 2, center panel). Favored QUDs receive a prior probability of 0.9; other QUDs receive a prior probability of 0.1/2 = 0.05. Holding the other priors at their default values, we see an increase in utterance endorsement from the none? (0.38) to how-many? (0.48) to all? (0.63) QUD. So, utterance endorsement is at its lowest when we believe the QUD is about whether none of the horses jumped; utterance endorsement is at is highest when we believe the QUD is about whether all of the horses jumped.
Finally, for the binary scope prior (Figure 2, right panel), we systematically manipulate the prior probability of inverse scope from 0.1 to 0.9. Holding the other priors at their default values, we see a monotonic increase in utterance endorsement as the probability of inverse increases. The model predicts an endorsement probability of 0.57 when the prior probability of inverse is at its highest (0.9)—at its lowest (0.1), endorsement drops to 0.42. So, the more accessible the inverse interpretation, the more utterance endorsement increases—though notably, the change is less than the endorsement rate changes that occur by altering the pragmatic factors.
To summarize, the world state and QUD priors have a more dramatic impact on utterance endorsement than the scope prior. There are two main reasons for these predictions. First, for the world state prior, when expectations favor success, the ambiguous utterance is maximally informative regardless of the scope interpretation it receives: amb communicates to a listener that prior expectations do not hold (i.e., None/Not all of the horses succeeded goes against the expectation that all (two) horses would succeed, which is what high bsuc entails). So, amb is particularly useful for communicating about the a priori unlikely not-all world states that appear in the experimental scenarios.
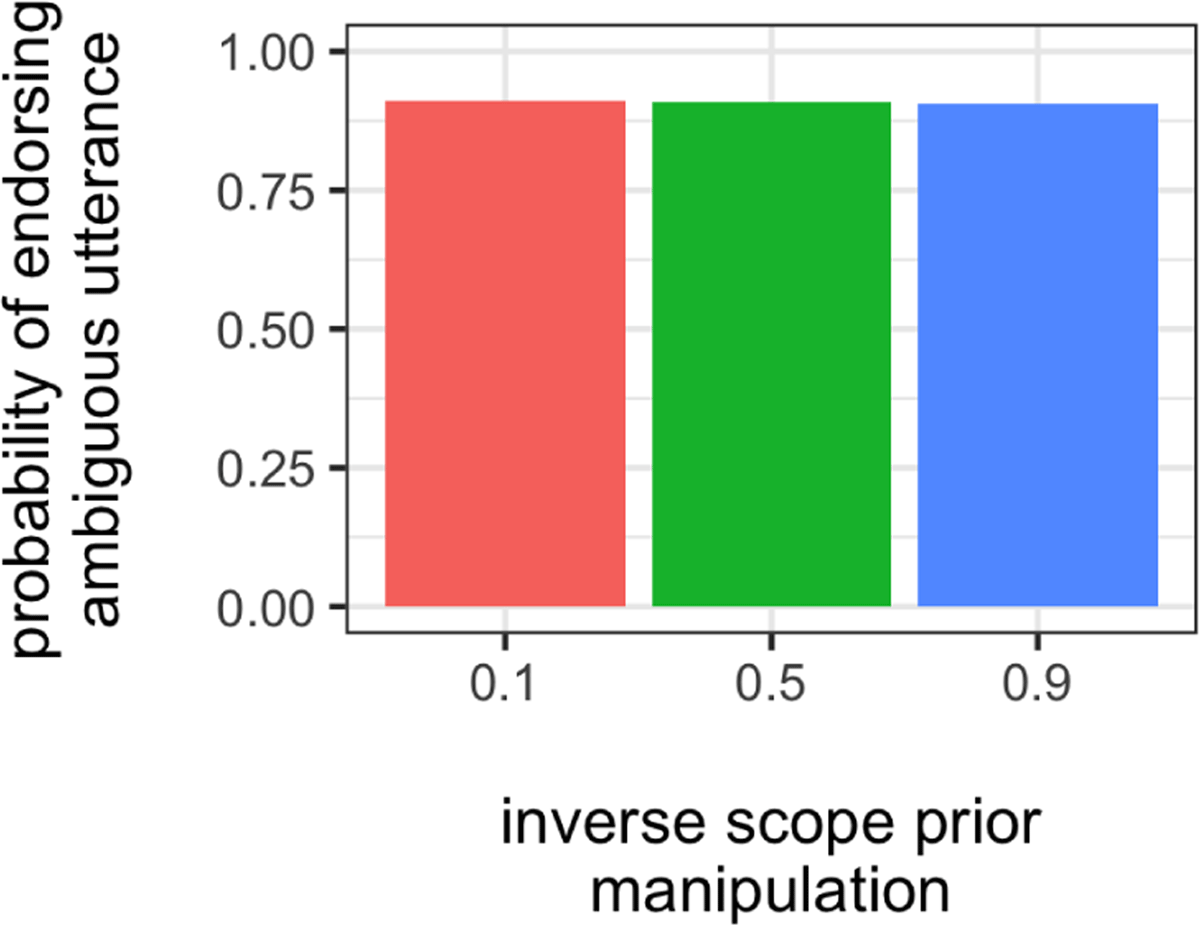
Second, for the QUD manipulation, when all? is favored, either interpretation of amb fully resolves the QUD: whenever amb is true (i.e., whether none or not all of the horses succeeded), it is not the case that all of the horses succeeded. A pragmatic speaker recognizes the utility of amb as an answer to all? in a not-all world state, irrespective of the intended scope interpretation. More generally, both pragmatic factors highlight that either scope interpretation will suffice if the right pragmatic context is present (a high bsuc or favoring the all? QUD). Thus, the model predicts that the grammatical processing factor (i.e., the inverse scope prior) should matter very little if both pragmatic factors are set so that either scope interpretation is informative. We demonstrate this prediction in Figure 3.
In particular, Figure 3 shows the interaction of all three factors for utterance endorsement when bsuc = 0.9 and all? are favored. We see the combined effects of the world state and QUD priors; together, they lead to near-total endorsement of the ambiguous utterance. We also see more clearly the relatively small contribution of the scope prior, where changing the prior probability of inverse from 0.1 to 0.9 leads to just a 0.002 change in endorsement probability. Thus, we see how the priors on the pragmatic factors overwhelm the processing factor of scope access. When the optimal QUD and world state are favored, even when inverse is highly inaccessible (i.e., P(inverse) = 0.1), we still predict high utterance endorsement (0.91). That is, even if the inverse scope is very inaccessible, the model predicts high rates of endorsement for the truth-value judgment task when a supportive pragmatic context is present.
3.3 Discussion
Our results suggest that when it comes to understanding non-adult-like behavior in the truth-value judgment task, there is a stronger role for the pragmatics of context management (as realized in priors on world state and QUD) than for grammatical processing (as realized in the prior on scope interpretations), although there may be a role for both. So, the observed failure of children to endorse scopally-ambiguous utterances in not-all scenarios likely stems more from children’s beliefs about the world of the experiment (e.g., whether horses are a priori likely to succeed) and about the topic of conversation (e.g., whether the conversational goal is to determine if all the horses succeeded) than an inability to grammatically derive or access the inverse scope interpretation. Indeed, our model predicts the highest rates of utterance endorsement when resolving the scope ambiguity is irrelevant for communicating successfully about the not-all world. In other words, the model predicts high endorsement whenever the pragmatic context is supportive—either because expectations favor total success or the QUD asks if all? of the horses succeeded—irrespective of how difficult it is to access the inverse scope. This prediction arises because both scope interpretations serve to inform a listener, either that the a priori likely w = 2 does not hold, or that the answer to the all? QUD is no. The pragmatic factors that lead to high utterance endorsement in our model yield situations where the every-not utterance serves as an informative description of the not-all state under either scope interpretation.
The non-adult truth-value judgment task behavior we see in children is predicted to stem from an inability to manage the pragmatic context as effectively as adults do; to become more adult-like in these scenarios, our model predicts that children must learn to adapt to less supportive pragmatic contexts in a way that makes the every-not utterance informative. Either the experience adults bring to bear on the communication scenario yields priors that are already pragmatically favorable (as opposed to children’s experience), or adults charitably adapt their priors in a way that recognizes the potential informativity of the every-not utterance. An adult-like adaptation ability might allow children to adjust their priors on either world state or QUD so that these variables have pragmatically-supportive values (e.g., bsuc = 0.9, P(all?) = 0.9), even when the actual context might not indicate such values. Importantly, we find that the scope prior alone is unable to deliver low (∼15%) endorsement rates that characterize some of the child behavior, or the high (∼100%) endorsement rates that characterize adult behavior. To generate more extreme predictions consistent with the behavioral patterns reported in the literature, our model predicts that the pragmatic factors must be involved.
Still, we might wonder if children’s inability to access or reason about alternatives plays a non-trivial role in their truth-value judgment behavior here. Indeed, the growing literature on this topic highlights children’s inability to access or reason with alternatives as a primary source of the divergences between child and adult pragmatic language behavior (e.g., Barner et al. 2011; Bale & Barner 2013). In the case of the judgment data that we model, perhaps there are utterance alternatives better-suited to describing the not-all scenarios, and adults—but not children—incorporate these alternatives into their truth-value reasoning. In the judgment data, any preference for these alternative utterances gets absorbed into the probability associated with choosing not to endorse the every-not test utterance. According to this reasoning, a participant would identify a better way of describing the not-all scenario and therefore choose not to endorse the utterance provided. This hypothesis therefore predicts that participants who are better able to reason about alternative utterances (i.e., adults) should endorse the scopally-ambiguous test utterance less often in the not-all scenario. Similarly, participants who are less able to reason about alternative utterances (i.e., children) should endorse the test utterance more often. Yet, the behavioral patterns go in the opposite direction: adults endorse the test utterance more than children do, not less. Therefore, we believe that children’s inability to reason about a broader set of utterance alternatives is unlikely to explain the behavioral patterns we have captured with our model.
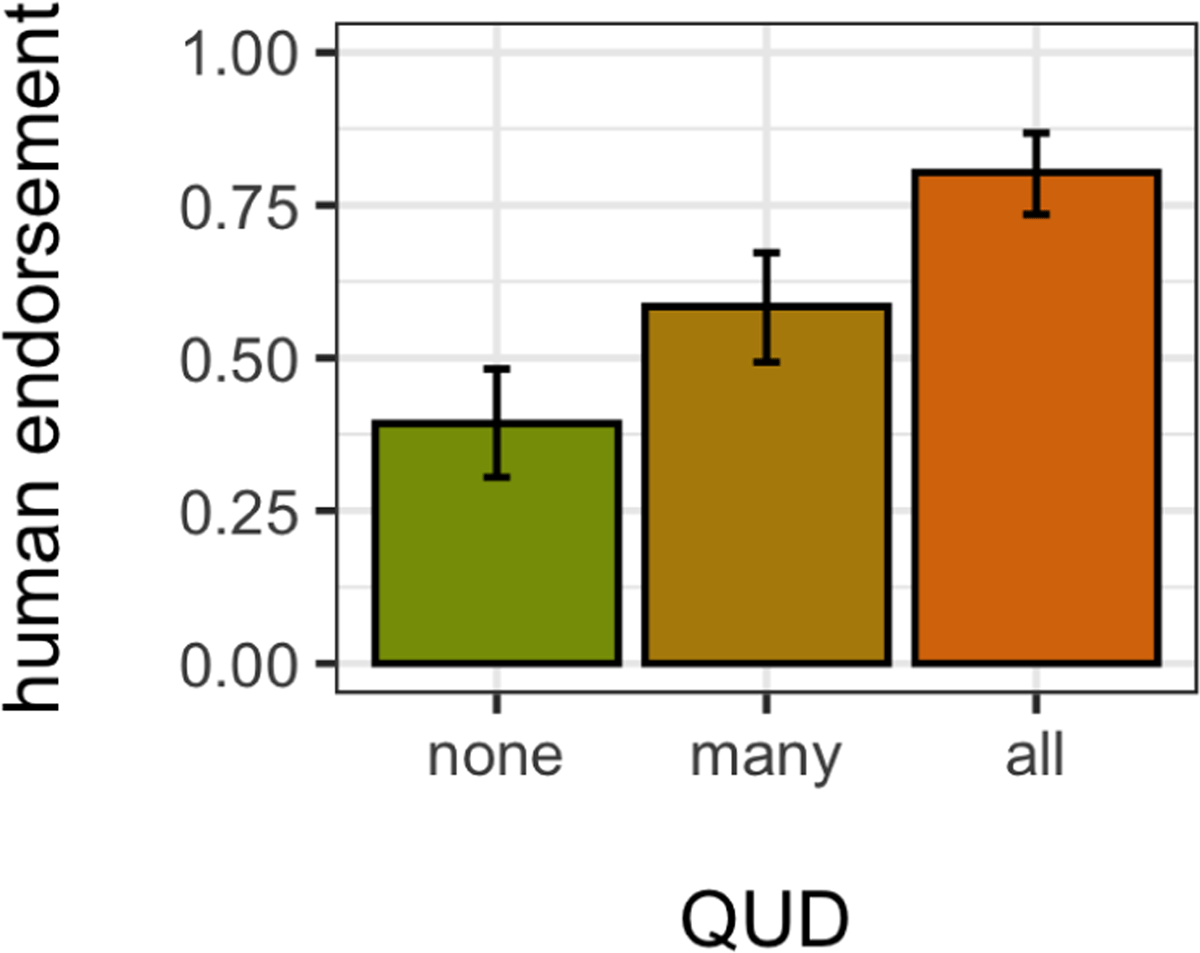
With respect to development, our modeling results suggest that adults and children are qualitatively similar in how they resolve scope ambiguity in context—by incorporating processing and pragmatic factors and recursively reasoning about speakers and listeners (as implemented in our RSA model); however, as noted above, the pragmatic factors (world states and QUDs) are predicted to have a stronger impact. If pragmatic factors do indeed matter as predicted here, we should find that similar contextual pressures affect endorsement behavior in both children and adults. In particular, we should be able to engineer less supportive pragmatic contexts—due to the priors on world states or QUDs—that yield lower endorsement rates also in adults, if adults are unable to repair the pragmatic context to give these variables more supportive values. Preliminary behavioral results suggest that adults are sensitive to QUD manipulations for every-not utterances precisely as our model predicts. In a modified truth-value judgment task that privileged different QUDs between subjects, Song et al. (2021) found that endorsement rates are at their highest when all? is privileged, intermediate for how-many?, and lowest for none? (compare Figure 4, from Song et al., with the model predictions in Figure 2, center panel). We build on this finding in the following section by exploring a case of ambiguity where adults start behaving like children.
Behavioral results from Song et al. (2021): English speakers’ endorsement of the every-not utterance as a good description of a not-all scenario, for three different QUDs (none?, how many?, and all?). Error bars represent bootstrapped 95% confidence intervals.
4 Two-not: When adults behave like children
Over the course of three truth-value judgment tasks, Musolino & Lidz (2003) demonstrated that adults are sensitive to some of the same experimentally-manipulated factors as children when it comes to endorsing scopally-ambiguous utterances. Rather than looking at every-not sentences, Musolino & Lidz investigated sentences with negation and cardinal numerals like two, as in (4). As with every-not, these two-not sentences admit two interpretations, corresponding to the relative scope of the logical operators introduced by the numeral and negation.
| (4) | Two horses didn’t jump over the fence. | |
| a. | Surface scope (∃ > ¬): | |
| There are two horses that didn’t jump over the fence. | ||
| b. | Inverse scope (¬ > ∃): | |
| It’s not the case that there are two horses that jumped over the fence. | ||
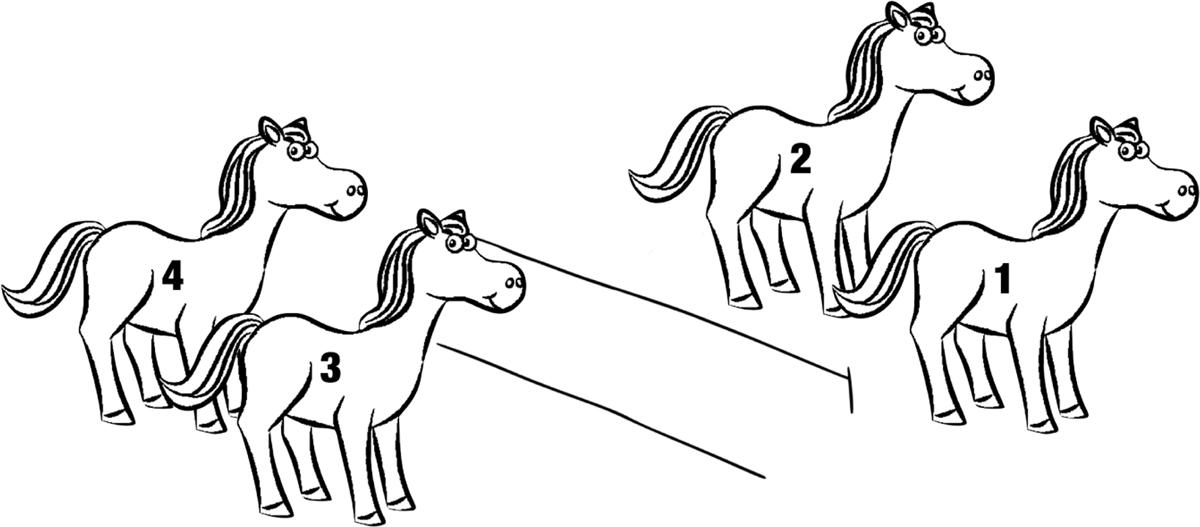
One scenario that distinguishes between these interpretations is shown in Figure 5, where there are four horses total and two (horses 1 and 2) jumped over the fence while another two (horses 3 and 4) did not. Here, the surface interpretation is true: there are in fact two horses, horses 3 and 4, that did not jump over the fence. In contrast, the inverse interpretation is false: there are two horses that jumped over the fence (horses 1 and 2).
In the first task of Musolino & Lidz (2003), adults heard two-not sentences in a context where both interpretations were true. For example, the scenario might have one out of three horses jumping over a fence; the surface interpretation is true because there are two horses who did not jump; the inverse interpretation is also true because it is not the case that there are two horses who did jump. After deciding whether to endorse the utterance, participants then justified their response so that their scope interpretation could be inferred. For example, if their explanation referred to the two horses that did not jump, then it was assumed that participants accessed the surface interpretation (there are two horses that didn’t jump). However, if the explanation referred to only one horse jumping, then it was assumed that participants accessed the inverse interpretation (only one horse jumped, so it’s not the case that two did). Musolino & Lidz found that all participants endorsed the utterance, and the explanations provided indicated a strong surface scope bias (75% surface, 7.5% inverse, 17.5% unclear from explanation). The authors interpreted this finding as evidence that adults prefer the surface interpretation of two-not utterances when both interpretations are true in context.
In the second task, adults heard a two-not sentence in two different contexts. The first context included two actors (e.g., horses), with one actor successfully completing the action (as in Figure 1; e.g., horse 1 jumped while horse 2 didn’t). In this 1-of-2 context, the surface interpretation is false (only one horse didn’t jump, so it is false that two horses didn’t jump), but the inverse interpretation is true (only one horse did jump, so it is indeed not the case that two horses jumped). Adults exhibited low endorsement (27.5%) for these 1-of-2 contexts.
In the second context, there were four actors. For example, four horses attempted to jump over a fence; two jumped and two did not, as in Figure 5. In this 2-of-4 context, the surface interpretation of the scopally-ambiguous two-not utterance is true: there are two horses that did not jump (horses 3 and 4 in Figure 5). However, the inverse interpretation is false because there are two horses that did jump (horses 1 and 2). In these contexts, adults had an endorsement rate of 100%.
Musolino & Lidz interpreted this asymmetry in endorsement rates between the two types of contexts, 1-of-2 vs. 2-of-4, as a strong surface scope preference in adults. According to this explanation, non-endorsement occurs in the 1-of-2 context because only the inverse scope is true; in contrast, endorsement occurs in the 2-of-4 context because the surface scope is true. That is, both patterns arise because adults favor the surface interpretation. While we find this account compelling, we note that there are other differences between the two contexts that might lead to the observed asymmetry. For example, it could be that the seemingly benign change from two to four total actors affects the pragmatic context. Another variable is the potential ambiguity present in the numeral semantics, which only becomes relevant in the 2-of-4 context—we return to this ambiguity in the following subsection. In either case, exploring the effects of these factors in a formal model of truth-value judgment behavior like the one we implemented above can clarify the process potentially underlying utterance disambiguation. Before presenting such a model, we review one additional experiment that investigates the impact of different experimental context manipulations on adult judgments. In particular, Musolino & Lidz set out to determine whether adults are affected by the same factors as children when it comes to increasing utterance endorsement for scopally-ambiguous utterances.
In their third task, Musolino& Lidz tested adults in 1-of-2 contexts using an early-success manipulation familiar from the child truth-value judgment experiments reviewed above. With an early-success manipulation, adults saw a positive contrasting clause describing successful outcomes before the utterance of interest, as in (5).
| (5) | Two horses jumped over the rock, but |
| two horses didn’t jump over the fence. |
Adults responded just as the children did to the early-success contexts, shifting to strong endorsement (92.5%; cf. 27.5% endorsement without the explicit contrast). However, as Musolino & Lidz note, it is not obvious why the adult endorsement rate increases when the early-success contrast is present.
Here is where our model of utterance endorsement might be able to help: just as we did with every-not utterances, we can model utterance endorsement for two-not utterances in an attempt to formally explicate the contribution of context to the observed endorsement behavior. In the process, we can also again test the hypothesis of continuity in the development of scope ambiguity resolution: if the same model architecture can capture both child and adult behavior, we have strong support for the hypothesis that children and adults are employing the same disambiguation mechanism, as implemented in the model.
4.1 Model specification
Our two-not model is a direct extension of the every-not model presented above.9 As before, we take world states w ∈ W to correspond to the number of successful outcomes; the world success base rate bsuc determines the probability that an individual will succeed. We continue to assume a simple truth-functional semantics where an utterance u denotes a mapping from world states to truth values. As before, we parameterize this truth function so that it depends on the scope interpretation i ∈ I = {inverse, surface}, ⟦u⟧i: W → Bool. We consider two alternative utterances u ∈ U: the null utterance (i.e., saying nothing at all, which we take as equivalent to choosing not to endorse the utterance) and the scopally-ambiguous two-not utterance amb (e.g., Two horses didn’t jump over the fence).
To fix the utterance semantics, we must consider potential ambiguity introduced by the numeral in cases where the number of relevant individuals n exceeds the numeral’s value. For example, consider the positive utterance Two horses jumped over the fence. If we assign an exact (=) semantics to the utterance, it will be true only when two horses succeeded. If we assign an at-least (≥) semantics, the sentence will be true when two or more horses succeeded. In worlds with only two horses, the exact vs. at-least distinction makes no difference: the sentence will be true in the world where both horses succeed, and false in all other worlds. However, in a scenario with four horses, the numeral semantics will define different truth-functional mappings. With the exact semantics, the sentence is true in any world where two horses—but not more—succeed. With the at-least semantics, the sentence is true in a larger set of worlds, where two or more horses succeed.
To evaluate the potential contribution of utterance semantics to the 1-of-2 vs. 2-of-4 asymmetry, we consider two different sets of utterance alternatives, one with amb= and another with amb≥. So, U= = {null, amb=} and U≥ = {null, amb≥}. The utterance semantics in (6) shows that scope parameterization i only impacts the truth conditions for amb utterances.
| (6) | Utterance semantics ⟦u⟧i: | |
| a. | ⟦null⟧i = true | |
| b. | ⟦amb=/≥⟧i = if i = inverse, then ⟦inverse=/≥⟧, else ⟦surface=/≥⟧ | |
| where: | ||
| ⟦inverse=⟧ = λw. w ≠ 2 | ||
| ⟦surface=⟧ = λw. if max(W) = 2, then w = 0, else w = 2 | ||
| ⟦inverse≥⟧ = λw. w < 2 | ||
| ⟦surface≥⟧ = λw. w < 3 | ||
In our horse-jumping scenario, the inverse= interpretation returns true just in case the number of horses that jumped is not equal to two (so w ≠ 2, which means the number could in fact be 3 or 4, or 0 or 1). Similarly, surface= returns true just in case the number of horses that did not jump is equal to two; in a world with two horses, this requirement means that zero horses jumped (w = 0), and in a world with four horses, this requirement means that exactly two horses did jump (w = 2). For the at-least interpretations, inverse≥ returns true just in case the number of horses that jumped is less than two. That is, if it is not the case that at least two horses jumped, then zero horses or only one horse jumped (and so w ∈ {0,1}, which is equivalent to w < 2). The at-least surface≥ returns true just in case the number of horses that jumped is less than three. That is, if at least two horses did not jump, then two, three, or four did not jump, which means two, one, or zero did jump (so w ∈ {0,1,2}, which is equivalent to w < 3).
We consider five potential QUDs q ∈ Q, three from the every-not model: (i) “How many horses succeeded?” (how-many?), (ii) “Did all of the horses succeed?” (all?), and (iii) “Did none of the horses succeed?” (none?). We also consider two additional QUDs specific to the two-not utterance: (iv) “Did exactly two horses succeed?” (two=?), and (v) “Did at least two horses succeed?” (two≥?). We add the two? QUDs under the assumption that by explicitly mentioning a numeral, that cardinality may be directly relevant to the topic of conversation. The QUDs behave as in (7).
| (7) | QUD semantics ⟦q⟧: | |
| a. | ⟦how-many?⟧ = λw. w | |
| b. | ⟦all?⟧ = λw. w = max(W) | |
| c. | ⟦none?⟧ = λw. w = 0 | |
| d. | ⟦two=?⟧ = λw. w = 2 | |
| e. | ⟦two≥?⟧ = λw. w ≥ 2 | |
4.2 Model predictions
To generate model predictions for adult sensitivity to the pragmatic contrast manipulation and the 1-of-2 vs. 2-of-4 asymmetry, we fix various model parameters. For 1-of-2 data, we set the number of individuals to 2 (i.e., max(W) = 2); for 2-of-4 data, we set the number of individuals to 4 (max(W) = 4). The S1 speaker rationality parameter α > 0 is set to 1. As before, the priors P(w) and P(q) correspond to expectations for the discourse context, with more extreme probabilities corresponding to more categorical beliefs. In the default case, we set the individual success base rate bsuc to 0.5 and we set P(q) so that the relevant QUDs have equal prior probability. The interpretation prior P(i) corresponds to how easy it is to access the inverse scope interpretation, with values near 0 indicating the inverse scope interpretation is very inaccessible relative to the surface scope interpretation. In the default case, P(inverse) = P(surface) = 0.5. As with the every-not model, we can independently manipulate the values of the priors on W, Q, and I, and observe their impact on utterance endorsement in order to better understand utterance endorsement behavior with scopally-ambiguous utterances.
Recall the empirical phenomena we are trying to capture: (i) the dramatic increase in endorsement rates in the 1-of-2 context when an explicit contrast is present, and (ii) the stark asymmetry in utterance endorsement rates between 1-of-2 and 2-of-4 contexts. We report results for each phenomenon in turn.
4.2.1 The explicit-contrast effect for 1-of-2
We can attempt to capture the increase in ambiguous utterance endorsement rates by systematically manipulating the pragmatic and processing factors, as implemented in the relevant priors. In a 1-of-2 context, the two-not model predictions are identical to the predictions of the every-not model in Figure 2 above—the models align because the ambiguous two-not and every-not utterances, for both scope interpretations, wind up true of exactly the same world states when W = {0, 1, 2}. That is, the surface interpretation for the every-not utterance holds that all (i.e., two) horses failed to jump over the fence (i.e., w = 0); the surface interpretation for the two-not utterance is the same: two (i.e., all) horses failed to jump (w = 0). The situation is similar for the inverse interpretation: every-not is true when not all of the horses jumped over the fence (i.e., w = 0, 1), and two-not is true when the number of horses that jumped is not two (w = 0, 1).
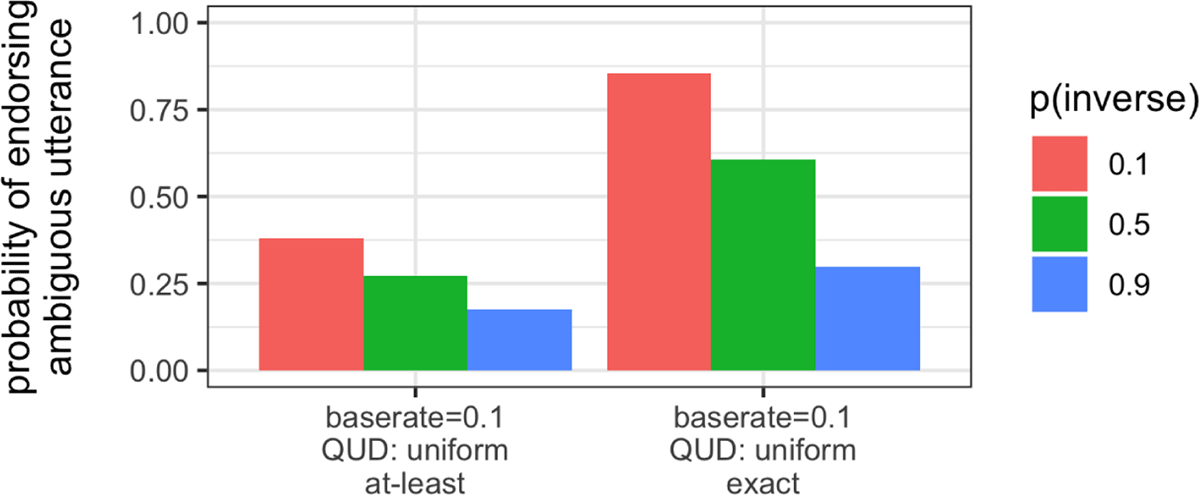
By replicating the results of our manipulations for the every-not model, each prior manipulation for the two-not model qualitatively captures the response pattern from Musolino & Lidz (2003). In particular, as before, the pragmatic factors controlling world and QUD beliefs have a more pronounced effect than the grammatical processing factor controlling scope access; the model’s world prior base rate manipulation comes closest to capturing the experimentally-observed effect of explicit-contrast manipulation (i.e., 27.5% base endorsement vs. 92.5% endorsement with the explicit contrast).
Just as before, we can also amplify the effect of the world base rate manipulation by allowing it to interact with the other factors. Specifically linking this manipulation to the experimental context, the early-success explicit-contrast manipulation possibly affects two aspects of the disambiguation calculus. First, it could increase expectations for success (i.e., a high bsuc if all (two) horses recently succeeded at jumping over something); second, it could shift the topic of conversation to whether total success was achieved again (i.e., a high prior on the all? QUD). To model the gangup of factors, Figure 6 plots the interaction of the world and QUD priors, together with the effect of scope.
The right side of Figure 6 replicates Figure 3: we see that access to the inverse scope has very little impact on the endorsement rate. This contrasts with the left side of Figure 6, where a low base rate (bsuc = 0.1) and a uniform prior on QUDs (so all? isn’t favored) lead access to the inverse scope to have a noticeable effect, with endorsement increasing with the prior probability of the inverse interpretation. Given these predictions, it seems that the empirically-observed low-endorsement baseline (27.5%) most likely results from low expectations for success (bsuc = 0.1) and QUD uncertainty (QUD: uniform), together with a moderate-to-low probability of accessing the inverse scope (P(inv) = 0.1 or 0.5). From this baseline, we can implement the effect of the explicit-contrast manipulation by increasing success expectations (bsuc = 0.9) and shifting the topic of conversation to whether total success occurred (QUD: all?). This manipulation results in a dramatic increase in utterance endorsement, irrespective of scope.
To summarize, if the explicit-contrast clause impacts a listener’s beliefs about the horses’ chance of success (increasing bsuc) or the QUD (favoring all?), then the model predicts the endorsement rate should increase. Notably, both of these manipulations make the two-not scopally-ambiguous utterance more informative for a listener. In the case of the world state manipulation, two-not—under either scope interpretation—informs the listener that her prior beliefs about total horse success do not hold. Similarly, with the QUD manipulation favoring all?, both scope interpretations answer this question in the negative (i.e., it is not the case that all (two) horses succeeded).
4.2.2 The 1-of-2 vs. 2-of-4 asymmetry
Our model predicts that these factors should be active in utterance disambiguation more generally; therefore, we can test the model’s hypothesis about the process of utterance disambiguation by seeing if the same model implementation used to capture 1-of-2 endorsement behavior can capture 2-of-4 endorsement behavior. More specifically, we would expect the very same pragmatic factors and values to additionally capture the high endorsement rate in the 2-of-4 context without the explicit contrast. If so, we would have computational modeling evidence that the factors identified for capturing the experimentally-observed effect of the explicit contrast could indeed be active in utterance disambiguation more generally.
Recall the baseline 1-of-2 parameter values most likely to lead to low endorsement: low expectations for success (bsuc = 0.1) and QUD uncertainty (QUD: uniform). To model the 2-of-4 context, we change the number of actors n to 4 and additionally manipulate whether the exact (=) or at-least (≥) utterance semantics applies, as predictions diverge when there are more than two actors in the context (recall the discussion in Section 4.1). This decision impacts both the utterance semantics and the relevant set of QUDs (e.g., if the at-least semantics gets used, then the two≥? QUD is included in the set of potential QUDs).
As shown in Figure 7, we do indeed predict high endorsement with the same parameter value baseline, but only with exact utterance semantics and a fairly low probability of accessing the inverse scope (P(inv) = 0.1). This prediction is shown on the right side of Figure 7, where a high endorsement rate is predicted with the pragmatic factors identified above (bsuc=0.1, QUD prior is uniform), as long as the numeral two has an exact semantics and access to inverse scope is low (P(inv) < 0.5). In contrast, when two has an at-least semantics (left side of Figure 4), the model predicts low endorsement with these pragmatic factors.
4.3 Discussion
Our model of two-not utterances—a straightforward extension of the every-not model—captures the effect of the early-success explicit-contrast manipulation observed in adults. Notably, we saw that the every-not model captures the same effect in children. This parallelism—sensitivity to the pragmatic context in both children and adults across different contexts—suggests that the same disambiguation mechanism could be active in both children and adults. Adults seem better able to charitably interpret less supportive pragmatic contexts (i.e., the original every-not scenarios; cf. the Principle of Charity from Gualmini et al. 2008); yet, there remain scenarios (i.e., the 1-of-2 two-not contexts) where even adult abilities to accommodate less supportive contexts are exceeded. We interpret the common underlying mechanism as support for developmental continuity in scope ambiguity resolution. That is, according to our model, no qualitative shift is required for five-year-old children to become adult-like in how they resolve scope ambiguity in context, as the same utterance interpretation process is used that incorporates pragmatic and processing factors and reasons recursively about speakers and listeners. Instead, the developmental change involves being able to adopt supportive values for various pragmatic factors, despite those values not being indicated by the current context, so that the speaker’s utterance can be charitably interpreted as informative.
The model also captures Musolino & Lidz’s results from the 2-of-4 context: with the very same parameter values that yield low endorsement rates for 1-of-2 contexts, the model predicts the high endorsement observed for 2-of-4 contexts. The only change is increasing the number of relevant individuals from two to four. This exploration of the 1-of-2 vs. 2-of-4 contexts allows us to refine our understanding of the potential sources of child and adult behavior. Our findings from the every-not model suggested that pragmatic factors alone are capable of capturing the non-adult-like behavior in children, and the extension in the current model captures the explicit-contrast effect in adults; however, it appears that the processing factor of scope access (in particular, disfavoring the inverse scope) is needed to account for Musolino & Lidz’s adult 2-of-4 results. This finding supports the conclusion of Musolino & Lidz, namely that adults have a strong preference for surface interpretations of two-not utterances. Combined with the appropriate pragmatic context, that preference has the potential to drive the endorsement asymmetry between the 1-of-2 and 2-of-4 contexts. Whether this surface-interpretation preference for two-not utterances is also something children share remains an open empirical question; experimental results for every-not do not answer this question definitively (Viau et al. 2010).
Interestingly, the current model requires one more ingredient to account for the 1-of-2 vs. 2-of-4 difference in adult behavior: an exact semantics for utterances with numerals (in contrast to an at-least semantics; for discussion, see, e.g., Geurts 2006; Breheny 2008). While the underlying utterance semantics is not something easy to manipulate in an experiment, it is exactly the kind of variable we can systematically explore in a computational cognitive model. By doing so here, we are able to show the necessity of an exact semantics in generating observable adult behavior. This result provides empirical support, coming from computational cognitive modeling, for theories about the semantics and pragmatics of numerals. In particular, we account for the observed adult behavior by assuming that adults interpret two-not utterances as meaning exactly two and not at least two.
5 General discussion
Truth-value judgments serve a critical role in diagnostics of linguistic meaning, yet the cognitive processes involved in generating these judgments—particularly the precise impact of context on pragmatic reasoning—have rarely been formally examined. Here, we have formally investigated the cognitive underpinnings of the truth-value judgment methodology. We used as our case study the phenomenon of scope ambiguity, where children’s behavior often deviates noticeably from that of adults; yet, both child and adult behavior can be profoundly affected by changes to task setups. Using the methodology of computational cognitive modeling, we advanced precise hypotheses about how linguistic knowledge, world knowledge, and general social reasoning interact to deliver observed behavior in the truth-value judgment task. To the extent that our model captures the data we set out to predict, we have found support for the hypothesis our model encodes, which specifies how pragmatic and processing factors interact to generate observed truth-value judgment behavior.
While we believe it is possible (and perhaps even likely) that other models with different assumptions may also be able to capture the judgment behavior, our aim here has been to test the viability of our hypothesis—an existence proof—rather than performing model comparisons. Importantly, our hypothesis relies on cognitively-plausible and independently-motivated assumptions about language understanding as implemented within the RSA framework. Our hope is that by formalizing our hypothesis (and assumptions) in the form a computational cognitive model, we will invite criticism, refinement, and further progress on the issue of scope ambiguity resolution. An exciting area for future work is to specify alternative hypotheses via computational cognitive models, and see if those models too can capture the behavior patterns that our hypothesis here does. While we believe it is likely that other models will also be able to account for the behavioral patterns discussed here, the true test of future, alternative models will be in the soundness of the assumptions they encode.
In the meantime, the findings from our model here lead to interesting considerations about how perceived usefulness may impact utterance endorsement in the truth-value judgment task, how children may differ from adults in this task (and so what development involves), and how generalizable this model of scope ambiguity resolution may be. We discuss each of these issues in turn.
5.1 Perceived usefulness for communication
Our model of utterance endorsement in the truth-value judgment task predicts the lowest rates of utterance endorsement for ambiguous utterances in not-all scenarios (as in Figure 1) when neither interpretation—surface or inverse—is useful for successful communication. We saw that two aspects of the pragmatic context have an outsized effect on predicted utterance endorsement, and for similar reasons. When the ambiguous utterance provides a full answer to the QUD under either scope interpretation, we recognize the ambiguous utterance as an informative thing to say, and so participants are more likely to find it useful and endorse it as a communicative act. For example, in a not-all horse-jumping scenario like Figure 1, if we care about whether all of the horses jumped, either interpretation is informative—both the surface and the inverse interpretations tell us that the answer is “no”. When prior beliefs about the world context and what counts as a likely state of affairs are contradicted by the ambiguous utterance—again, under either scope interpretation—the utterance is potentially very informative, which makes it more useful and thus more likely to be endorsed. For example, in a not-all scenario, if we think horses nearly always succeed in jumping, we would expect the world where all the horses are successful to be most likely; here, either interpretation is informative because both the surface and the inverse interpretations tell us that the world where all the horses are successful is in fact not the one we are in.
Given these observations, our model suggests that the utterance non-endorsement behavior that has been previously used to demonstrate children’s difficulty with inverse scope calculation in fact requires no disambiguation at all if the goal is informative communication (as mentioned above, both interpretations can be more or less informative in certain pragmatic contexts). Instead, participants simply need the ability to manage the pragmatic context so they can recognize the potential informativity of these ambiguous utterances; more specifically, participants must already have priors that support informativity, or be able to adjust those priors upon realizing that the ambiguous utterance is not informative. Adjusting the pragmatic context to increase the informativity of an utterance is what could allow participants to “charitably” endorse the utterance (Gualmini et al. 2008). In our modeling framework, adjusting the pragmatic context amounts to using priors for QUDs and world states that yield a true and informative statement (e.g., a high base rate of success and a QUD about whether all the horses succeeded), even if those prior beliefs may not be supported already by the immediate discourse context.
5.2 Children vs. adults, and implications for development
Considerations of pragmatic context have long played a role in the design and interpretation of the truth-value judgment task for children (e.g., Crain et al 1996). Here we have taken the extra step of formally articulating hypotheses regarding specific pragmatic factors and the role they play in children’s apparent difficulty with ambiguous utterances in the truth-value judgment task. In this way, we can specify how changing the experimental context impacts the pragmatic factors that underlie children’s truth-value judgment endorsement behavior. That is, we identify both (i) how the manipulations to the experimental context could impact these pragmatic factors, and (ii) why impacting them this way increases the informativity of the utterance and so leads to more endorsement.
Our results suggest that, in order to endorse the ambiguous utterance, truth-value judgment experimental participants must be able to manage the pragmatic context in a way that allows them to recognize the potential utility of the ambiguous utterance; in our modeling framework, managing the pragmatic context amounts to using priors for QUDs and world states that yield a true and informative statement, even if those prior beliefs may not be supported already by the immediate discourse context. While our results from the two-not case study suggest developmental continuity in the ambiguity-resolution mechanism, we speculate that the ability to charitably adjust the assessment of the pragmatic context could separate children from adults and is the aspect of linguistic ability that would still need to develop in five-year-olds (in line with Conroy 2008, who notes that five-year-olds struggle to modulate their interpretations on the basis of task-specific discourse information). In particular, we hypothesize that five-year-olds struggle to make this pragmatic context adjustment and instead rely on the pragmatic context presented. Given the differing amounts of life (and language) experience between children and adults, it seems plausible that the two groups could arrive at different priors for the pragmatic factors in our model given the same experimental context, and have different amounts of practice repairing unsupportive pragmatic contexts.
However, with two-not utterances, even adults require additional support to manage the pragmatic context in certain scenarios. In other words, the ability that facilitates charitable interpretation may be specific to the quantifier combination involved, since adults appear less able to deploy the repair skill for two-not utterances. At least two factors may be at play. First, adults could have different amounts of experience with every-not vs. two-not utterances, so that they have more experience repairing every-not utterances. That is, adults’ superior repair ability with every-not is due to experience. Second, the two-not utterance may be inherently more difficult to process. That is, adults’ superior repair ability with every-not is due to something about every and not appearing together, when compared with two and not appearing together. For instance, Conroy (2008) suggests that the time it takes to verify one interpretation versus another in a particular context impacts adult interpretation preferences. So, it could be that verification of the inverse interpretation in these contexts is harder for two-not compared to every-not. It could also be that both factors contribute to adults’ resistance to endorsing two-not utterances in the absence of supportive pragmatic contexts. With respect to development, given that adults struggle with two-not more than every-not for either (or both) of these reasons, we also expect children to struggle more with two-not. That is, the target state for development would be the ability to repair the pragmatic context (if necessary) for every-not, but not for two-not. In this way, five-year-olds—who struggle to repair the pragmatic context in general—would already be adult-like for two-not.
While it remains an open question why every-not but not two-not utterances should be repairable by adults, our modeling does predict one difference between the utterances: with two-not, we predict a strong bias for surface scope, whereas no such bias is necessary to yield the predicted high endorsement for every-not utterances. If this prediction is on the right track, then future work can determine if and when this bias is indeed active in adults who are asked if they endorse these kinds of ambiguous utterances; existing behavioral work aligns with adults having a surface scope bias, as they seem to pursue a surface scope interpretation first for every-not utterances (Conroy 2008; Conroy et al. 2008). So, a surface scope bias may always be present in adults. For children, findings from Conroy (2008) suggest that four-year-olds do not seem to have a surface scope bias, while five-year-olds do. If so, then becoming adult-like would involve developing a surface scope bias, which may have developed already in five-year-olds, but not four-year-olds.
5.3 Generalizability of our model of ambiguity resolution
Recent computational and empirical work by Attali et al. (2021) has also found independent support for our model of ambiguity resolution—and the importance of pragmatic factors—for interpreting scopally-ambiguous utterances besides every-not and two-not utterances. In particular, Attali et al. extended the very same model architecture to predict adult interpretations for some-not (e.g., some of the horses didn’t jump over the fence) and no-not (e.g., none of the horses didn’t jump over the fence), and then verified the extended model predictions in a paraphrase-endorsement task measuring interpretation preferences. The same model architecture presented here (with fixed parameter values across the three utterances) seamlessly captures human behavior for this broader range of utterances, further supporting the specific pragmatic context hypothesized by our model to yield human interpretation behavior.
Given this strong support for the generalizability of our model across quantifier-negation structures, one might be tempted to generalize the model to cases of scope ambiguity without negation (e.g., doubly-quantified utterances like a horse jumped over every fence). While we believe such explorations will further inform our understanding of ambiguity phenomena, it is important to recognize that quantifier-negation utterances and doubly-quantified ones may have different processing signatures (e.g., Chemla & Bott 2015 found that every-a and a-every have different results than every-negation with respect to priming); so, doubly-quantified utterances may rely on different ambiguity-resolution mechanisms than quantifier-negation utterances. Still, we believe that doubly-quantified utterances are ripe for a computational treatment of the sort we advance here, and that pressures from informativity and truth probability enter for those utterances as they do for quantifier-negation utterances.
6 Conclusion
Our findings underscore the complexity of information involved in interpreting scopally-ambiguous utterances, including the literal semantics of the utterances involved, processing factors that affect interpretation accessibility, pragmatic factors that affect the potential informativity of the utterance, and the recursive social reasoning between speakers and listeners. Our findings furthermore highlight the potential similarities between how children and adults resolve this kind of scope ambiguity in context. Over the course of two applications—explaining children’s non-adult-like behavior with every-not utterances and adults’ child-like behavior with two-not utterances—we find evidence for the impact of both pragmatic and processing factors on truth-value judgment behavior; in particular, we see how a specific confluence of values for these factors yields the observed utterance endorsement behavior in multiple contexts. The fact that the same pragmatic factors can have such a pronounced effect on both child and adult behavior highlights the possibility of developmental continuity in scope ambiguity resolution from childhood to adulthood. Moreover, the fact that the processing factor of scope access is crucial for explaining adult behavior in certain contexts (i.e., two-not utterances) motivates experimental work with children to see if their behavior is likewise affected by this processing factor in similar contexts.
More broadly, we have demonstrated how computational cognitive modeling can help us refine our theories about different aspects of language, including theories of language understanding, language development, and language representation. Importantly, we have shown how analytic results allow for a better understanding of behavior in the truth-value judgment task, thereby allowing for a better understanding of the task itself and thus a cleaner mapping between our cognitive theories of ambiguity resolution and the data that test them. The moral is as follows: before we can effectively interpret truth-value judgment behavior with respect to our theories of processing, development, and representation, we must understand the pragmatics involved; the current work offers a path toward that understanding.
Notes
- This version of the truth-value judgment task is known as “descriptive,” in the sense that participants first see the scenario and then encounter the utterance. The task may also be used in a “predictive” mode, where participants encounter the utterance before the scenario. For discussion, see Musolino (1998). [^]
- How that average rate arises is an interesting question—it could be that individual participants have an 80% probability of endorsement on a given trial, or it could be that 80% of participants have a 100% probability of endorsement on a given trial (with 20% of participants having a 0% probability). While the model is agnostic about this choice, we find the former option more plausible. [^]
- In an earlier formulation of the model (Savinelli et al. 2017), we manipulated the world state prior by assigning probabilities directly to the possible states, rather than using a success base rate to assign those probabilities; the model produced qualitatively the same behavior we report below for the current model. [^]
- We use notation that maximizes transparency to the implementation in the publicly-available code base at http://forestdb.org/models/kids-scope.html. [^]
- Recall that L0 is a naive, hypothetical reasoning agent imagined by the hypothetical speaker S1. So, when choosing utterances, S1 imagines how hypothetical, naive L0 would interpret the various utterances with respect to a specific scope interpretation and (as shown later on) QUD. [^]
- We are presenting a version of RSA where L0 does not take into account the state prior P(s) in calculating the posterior over states, which is a departure from the original formulation. For more on this choice, including empirical justification, see Qing & Franke (2015); Scontras et al. (electronic). [^]
- We note that by partitioning the possible world states, QUDs allow the modeled listener to shift the probabilities determined by the literal semantics. In fact, QUD manipulations were originally proposed within the RSA framework to handle non-literal language, where, by necessity, the probability determined by the literal semantics must shift; see Kao et al. (2014a; b) for additional discussion. [^]
- See Zaslavsky et al (2021) for a recent exploration of the role of α in RSA. RSA models also factor in the cost of the utterance, such that S1’s utility seeks to minimize utterance cost. We assume that our utterances are equally costly—neither response in the truth-value judgment task imposes a greater cost, as the participant is saying either “yes” or “no”—so the cost term cancels out. [^]
- See Savinelli et al. (2018) for an initial presentation of this model. [^]
Acknowledgements
The authors gratefully acknowledge the contributions of KJ Savinelli, who helped with earlier stages of this project. Thanks also to audiences at Stanford University, the University of Tübingen, the University of Florida, UC San Diego, the UConn Logic Group, CUNY 2017, CogSci 2017, CMCL 2018, LSA 2018, CIALT-2 2018, as well as to four anonymous reviewers and the QuantLang Collective at UC Irvine for helpful comments.
Competing Interests
The authors have no competing interests to declare.
References
Attali, Noa & Scontras, Gregory & Pearl, Lisa S. 2021. Pragmatic factors can explain variation in interpretation preferences for quantifier-negation utterances: A computational approach. In Proceedings of the 43rd annual meeting of the Cognitive Science Society, 917–923. DOI: http://doi.org/10.7275/3zax-6v78
Bale, Alan & Barner, David. 2013. Grammatical alternatives and pragmatic development. In Fălăuş, Anamaria (ed.), Alternatives in semantics, 238–266. Palgrave Press. DOI: http://doi.org/10.1057/9781137317247
Barner, David & Brooks, Neon & Bale, Alan. 2011. Accessing the unsaid: The role of scalar alternatives in children’s pragmatic inference. Cognition 118. 84–93. DOI: http://doi.org/10.1016/j.cognition.2010.10.010
Breheny, Richard. 2008. A new look at the semantics and pragmatics of numerically quantified noun phrases. Journal of Semantics 25(2). 93–139. DOI: http://doi.org/10.1093/jos/ffm016
Chemla, Emmanuel & Bott, Lewis. 2015. Using structural priming to study scopal representations and operations. Linguistic Inquiry 46. 157–172. DOI: http://doi.org/10.1162/LING_a_00178
Conroy, Anastasia & Fults, Scott & Musolino, Julien & Lidz, Jeffrey. 2008. Surface scope as a default: The effect of time in resolving quantifier scope ambiguity. Poster presented at the 21st CUNY Conference on Sentence Processing.
Conroy, Anastasia Marie. 2008. The role of verification strategies in semantic ambiguity resolution in children and adults: University of Maryland, College Park dissertation.
Crain, Stephen & McKee, Cecile. 1985. The acquisition of structural restrictions on anaphora. In Proceedings of NELS, vol. 15. 94–110.
Crain, Stephen & Thornton, Rosalind. 1998. Investigations in Universal Grammar: A guide to research on the acquisition of syntax and semantics. Cambridge, MA: MIT Press.
Crain, Stephen & Thornton, Rosalind & Boster, Carole & Conway, Laura & Lillo-Martin, Diane & Woodams, Elaine. 1996. Quantification without qualification. Language Acquisition 5(2). 83–153. DOI: http://doi.org/10.1207/s15327817la0502_2
Degen, Judith & Goodman, Noah D. 2014. Lost your marbles? The puzzle of dependent measures in experimental pragmatics. In Proceedings of the 36th annual meeting of the Cognitive Science Society, 397–402.
Denison, Stephanie & Reed, Christie & Xu, Fei. 2011. The emergence of probabilistic reasoning in very young infants. In Proceedings of the annual meeting of the Cognitive Science Society, vol. 33. 441–446.
Gerken, LouAnn. 2006. Decisions, decisions: Infant language learning when multiple generalizations are possible. Cognition 98(3). B67–B74. DOI: http://doi.org/10.1016/j.cognition.2005.03.003
Geurts, Bart. 2006. Take five: The meaning and use of a number word. In Vogeleer, Svetlana & Tasmowski, Liliane (eds.), Non-definiteness and plurality, 311–329. Amsterdam: Benjamins. DOI: http://doi.org/10.1075/la.95.16geu
Goodman, Noah D. & Frank, Michael C. 2016. Pragmatic language interpretation as probabilistic inference. Trends in Cognitive Sciences 20(11). 818–829. DOI: http://doi.org/10.1016/j.tics.2016.08.005
Goodman, Noah D. & Stuhlmüller, Andreas. 2013. Knowledge and implicature: Modeling language understanding as social cognition. Topics in Cognitive Science 5(1). 173–184. DOI: http://doi.org/10.1111/tops.12007
Gualmini, Andrea. 2004. Some knowledge children don’t lack. Linguistics, 957–982. DOI: http://doi.org/10.1515/ling.2004.034
Gualmini, Andrea. 2008. The rise and fall of isomorphism. Lingua 118(8). 1158–1176. DOI: http://doi.org/10.1016/j.lingua.2008.02.003
Gualmini, Andrea & Hulsey, Sarah & Hacquard, Valentine & Fox, Danny. 2008. The question-answer requirement for scope assignment. Natural Language Semantics 16(3). 205–237. DOI: http://doi.org/10.1007/s11050-008-9029-z
Jasbi, Masoud & Waldon, Brandon & Degen, Judith. 2019. Linking hypothesis and number of response options modulate inferred scalar implicature rate. Frontiers in Psychology 10. 189. DOI: http://doi.org/10.3389/fpsyg.2019.00189
Kao, Justine T. & Bergen, Leon & Goodman, Noah D. 2014a. Formalizing the pragmatics of metaphor understanding. In Proceedings of the 36th annual meeting of the Cognitive Science Society, 719–724.
Kao, Justine T. & Wu, Jean Y & Bergen, Leon & Goodman, Noah D. 2014b. Nonliteral understanding of number words. Proceedings of the National Academy of Sciences 111(33). 12002–12007. DOI: http://doi.org/10.1073/pnas.1407479111
Lassiter, D. & Goodman, N. D. 2013. Context, scale structure, and statistics in the interpretation of positive-form adjectives. In Semantics and Linguistic Theory (SALT) 23, 587–610. DOI: http://doi.org/10.3765/salt.v23i0.2658
Musolino, Julien. 1998. Universal Grammar and the acquisition of semantic knowledge: An experimental investigation into the acquisition of quantifier-negation interaction in English: University of Maryland, College Park Doctoral dissertation.
Musolino, Julien. 2006. Structure and meaning in the acquisition of scope. In Semantics in acquisition, 141–166. Springer. DOI: http://doi.org/10.1007/1-4020-4485-2
Musolino, Julien & Lidz, Jeffrey. 2003. The scope of isomorphism: Turning adults into children. Language Acquisition 11(4). 277–291. DOI: http://doi.org/10.1207/s15327817la1104_3
Musolino, Julien & Lidz, Jeffrey. 2006. Why children aren’t universally successful with quantification. Linguistics 44. 817–852. DOI: http://doi.org/10.1515/LING.2006.026
Pearl, Lisa. 2017. Evaluation, use, and refinement of knowledge representations through acquisition modeling. Language Acquisition 24(2). 126–147. DOI: http://doi.org/10.1080/10489223.2016.1192633
Pearl, Lisa. In press. Modeling syntactic acquisition. In Sprouse, Jon (ed.), Oxford Handbook of Experimental Syntax, Oxford, UK: Oxford University Press.
Qing, Ciyang & Franke, Michael. 2015. Variations on a Bayesian theme: Comparing Bayesian models of referential reasoning. In Zeevat, H. & Schmitz, H.-C. (eds.), Bayesian natural language semantics and pragmatics, 201–220. Springer. DOI: http://doi.org/10.1007/978-3-319-17064-0
Roberts, Craige. 2012. Information structure in discourse: Towards an integrated formal theory of pragmatics. Semantics and Pragmatics 5(6). 1–69. DOI: http://doi.org/10.3765/sp.5.6
Savinelli, K. J. & Scontras, Gregory & Pearl, Lisa. 2017. Modeling scope ambiguity resolution as pragmatic inference: Formalizing differences in child and adult behavior. In Proceedings of the 39th Annual Meeting of the Cognitive Science Society, 3064–3069.
Savinelli, K. J. & Scontras, Gregory & Pearl, Lisa. 2018. Exactly two things to learn from modeling scope ambiguity resolution: Developmental continuity and numeral semantics. In Proceedings of the 8th Workshop on Cognitive Modeling and Computational Linguistics (CMCL 2018), 67–75. DOI: http://doi.org/10.18653/v1/W18-0108
Scontras, Gregory & Goodman, Noah D. 2017. Resolving uncertainty in plural predication. Cognition 168. 294–311. DOI: http://doi.org/10.1016/j.cognition.2017.07.002
Scontras, Gregory & Tessler, Michael Henry & Franke, Michael. electronic. Probabilistic language understanding: An introduction to the Rational Speech Act framework. Retrieved from https://www.problang.org.
Song, Yongjia & Jimenez, Abimael Hernandez & Scontras, Gregory. 2021. Cross-linguistic scope ambiguity: An investigation of English, Spanish, and Mandarin. Proceedings of the Linguistic Society of America 6. 572–586. DOI: http://doi.org/10.3765/plsa.v6i1.4992
Tessler, Michael Henry & Goodman, Noah D. 2019. The language of generalization. Psychological Review 126. 395–436. DOI: http://doi.org/10.1037/rev0000142
Thornton, Rosalind. 2017. The truth value judgment task: An update. In Nakayama, Mineharu & Su, Yi-Ching & Huang, Aijun (eds.), Studies in Chinese and Japanese language acquisition: In honor of Stephen Crain, 13–40. John Benjamins Publishing Company. DOI: http://doi.org/10.1075/lald.60.02tho
Viau, Joshua & Lidz, Jeffrey & Musolino, Julien. 2010. Priming of abstract logical representations in 4-year-olds. Language Acquisition 17(1–2). 26–50. DOI: http://doi.org/10.1080/10489221003620946
Wason, Peter C. 1965. The contexts of plausible denial. Journal of Verbal Learning and Verbal Behavior 4(1). 7–11. DOI: http://doi.org/10.1016/S0022-5371(65)80060-3
Xu, Fei & Tenenbaum, Joshua. 2007. Word Learning as Bayesian Inference. Psychological Review 114(2). 245–272. DOI: http://doi.org/10.1037/0033-295X.114.2.245
Zaslavsky, Noga & Hu, Jennifer & Levy, Roger P. 2021. A Rate-Distortion view of human pragmatic reasoning. In Proceedings of the Society for Computation in Linguistics, Vol. 4. DOI: http://doi.org/10.7275/gc1z-ck09