1 Introduction
According to the standard analysis of ‘most’ and ‘more than half’, the sentences ‘most cats sleep’ and ‘more than half of the cats sleep’ are truth conditionally equivalent. More generally, ‘most As are B’ and ‘more than half of the As are B’ are verified by the same As and Bs. ‘Most As are B’ is analysed as conveying that the size of A ∩ B is greater than the size of A–B, whereas ‘More than half of As are B is analysed as conveying that the size of A ∩ B is greater than half the size of A (Hackl 2009):1
| (1) | ⟦most⟧(A)(B) ⟺ |A ∩ B| > |A – B| |
| (2) | ⟦MTH⟧(A)(B) ⟺ |A ∩ B| > |A| |
In contrast to this assumption, the behaviours of ‘most’ and ‘more than half’ differ. Early work has focused on the different behaviour of the two expressions with respect to their upper bounds (Ariel 2003) or their cognitive encoding, which has been argued to lead to different verification procedures (Hackl 2009). The main difference, which will be the focus of this paper, is that ‘most’ tends to be used to convey proportions higher than ‘more than half’. More specifically, while ‘more than half’ is usually used for proportions right above 50%, ‘most’ is used for proportions that are significantly higher than 50%. This difference between ‘most’ and ‘more than half’ calls for an explanation. Following Denić & Szymanik (Forthcoming), we can distinguish two classes of explanations for this difference.
First, lexical meaning hypotheses attempt to explain the difference in terms of a difference in the literal meanings of ‘most’ and ‘more than half’, plus possibly some additional pragmatic phenomena. Recent work has produced experimental evidence supporting the hypothesis of a semantic difference between the two expressions. Ramotowska et al. (2019) observe a difference in decision times and behaviour of subjects verifying sentences with the two quantifiers that are consistent with the model in which the threshold for ‘more than half’ is 50% and the threshold for ‘most’ is higher. Denić & Szymanik (Forthcoming) report that the thresholds of ‘most’ do not change under downward monotone environments and argue that this finding suggests that the difference between the two quantifiers is due to semantics (see original paper for a fuller explanation). The fullest theoretical development of the lexical meaning hypothesis for the difference between ‘most’ and ‘more than half’ has been developed in Solt (2016), which we explain in more detail in Section 2.
On the other hand, pragmatic strengthening hypothesis claims that while the two expressions have the same literal meaning, they are pragmatically strengthened in different ways. First, the upper bound of ‘more than half’ is inferred to be lower than 100% by scalar implicature, through competition with expressions such as ‘more than three quarters’. Second, ‘most’ is pragmatically strengthened in a way that results in a lower bound higher than ‘more than half’. This strengthening can happen, e.g., by competition with the enriched meaning of ‘more than half’, through a higher-order scalar implicature (Spector 2007) or an R-implicature.
In this paper, we give the first fully fleshed-out version of the pragmatic strengthening hypothesis. We argue that two independently needed mechanisms in the interpretation of quantifiers suffice to predict the difference between the two expressions without assuming a difference in scale structures or truth conditions. The first mechanism is the tendency of the listener to guess points central to a category to minimize the expected distance between their own guess and the speaker’s observation. The second mechanism is the structural theory of conceptual alternatives, which lets the alternative set of an utterance depend on the structure of the concept conveyed by the utterance. We show that these mechanisms make the correct predictions with a computational model of pragmatics, the Rational Speech Act model. We support our proposal with experimental data, showing that a hierarchical Bayesian model implementing our account can fit the production quantifier data.
2 Solt’s account
Solt (2016) offers a comprehensive review of the differences between ‘most’ and ‘more than half’. Solt (2016) considers all appearances of the two expressions as quantifiers in the nominal domain in the Corpus of Contemporary American English (COCA) (Davies 2017). Based on this data, the paper identifies differences in usage between the two expressions. For instance, the paper finds differences in how the two expressions are used with vague and uncountable domains and with vague predicates. However, in what follows, we will focus on differences in the proportions for which the two expressions are used. To compare these, those appearances were selected which included a specific percentage (n = 54 for ‘more than half’ and n = 141 for ‘most’). The corpus data shows that (1) ‘more than half’ is mainly used for percentages in the 50%–65% range, (2) ‘most’ has a much flatter distribution which covers the whole 50%–100% range, but rarely below 60%.
While the precise proportions reported in Solt (2016) are noisy estimates, the crucial observation is that the two expressions differ in the way they are used with respect to both their lower bounds and their upper bounds. The lower bound of ‘more than half’ is close to 50%, while the lower bound of ‘most’ is close to the upper bound of ‘more than half’. The upper bound of ‘more than half’ is much lower than 100%, while the upper bound of ‘most’ is close to 100%.
Solt (2016) also proposes an account of the difference between the two expressions. She gives a generalized form of 1 and 2:
| (3) | ⟦most⟧(A)(B) ⟺ μS(A ∩ B) > μS(A – B) |
| (4) | ⟦MTH⟧(A)(B) ⟺ μS(A ∩ B) > μS(A) |
Where μS is a measure function. Solt points out that the two logical forms 3 and 4 indicate a deeper semantic difference. Namely, the measure functions for the two expressions range over scales with different structures. Specifically, the logical form for ‘more than half’ encode division by two, and therefore uses a ratio scale, while ‘most’ can use the weaker structure of a semi-ordered scale (Stevens 1946). Two points on a ratio scale, such as the scale of weights, can be compared precisely to each other, and each of them can be compared to a proportion of the other. In contrast to ratio scales, a point on the type of semi-ordered scale Solt discusses can be represented as a whole distribution, which encodes uncertainty about the precise value in some precise underlying scale. For instance, the estimation of an object’s weight obtained just by lifting the object can be represented as a distribution on the physical scale of weights. Two points on such a scale can be distinguished from each other only when the distributions do not overlap excessively.2
Solt (2016) uses the difference between the two scale-types to explain why ‘most’ has a lower bound that is higher than that of ‘more than half’. If a language user’s measure of A ∩ B and B are on a ratio scale, A ∩ B can be compared precisely to half of the measure of A. Whenever such precise comparisons are possible, a speaker can utter expressions such as ‘more than half of the As are B’. This, in turn, allows the speaker to use ‘more than half’ for cases where the proportion of As that are B is close to 0.5. In contrast, an expression such as ‘most As are B’ only requires us to determine whether the size of A ∩ B is greater than the size of A – B, rather than calculating half the measure of A. However, since perceptible differences in semi-ordered scales require substantial differences between the points, ‘most As are B’ will only be uttered when the measure of A ∩ B is substantially greater than the measure of A – B. In sum, since ratio scales allow arbitrarily precise comparisons between points while semi-ordered scales require substantial differences, Solt’s account predicts the lower bound of ‘more than half’ to be closer to 0.5 than the lower bound of ‘most’, as observed in the corpus data.
Solt accounts for the difference in the upper bounds of the two expressions with a difference in the scalar implicatures they generate, still due to the two scale-types. Solt points out that ‘more than half’ has a rich set of alternative utterances, including ‘more than two thirds’ and ‘more than three quarters’. On the other hand, the alternative utterances to ‘most’ are more sparse, including ‘all’. Since the set of alternative utterances is more fine-grained for ‘more than half’ than for ‘most’, scalar implicatures constrain the upper bound of the former to be lower than the latter. Solt proposes that the two expressions have different sets of alternatives because each expression only alternates with expressions that use the same scale type.
Solt’s account, as summarized in this section, relies on a semantic difference between ‘most’ and ‘more than half’, specifically in the structure of the scales they use. As such, Solt (2016) belongs to the lexical meaning class of explanations. The next section introduces an alternative account that explains the difference between ‘most’ and ‘more than half’ without assuming a difference in the scales underlying the two expressions or any other semantic difference. While we have focused in this section on Solt’s explanation of the proportions that the two expressions typically describe, Solt’s account explains other differences between ‘most’ and ‘more than half’. In this paper, we will not attempt to apply our account to these further patterns, but leave this to future work.
3 Two mechanisms in the interpretation of quantifiers
In this section, we present our account informally, before formalizing it in Sections 4 and 5. Our account explains why ‘most’ and ‘more than half’ are typically used to convey different proportions, based on two mechanisms. The first is the idea that the listener attempts to minimize the difference between their guess and the speaker’s observation. The second is the fact that different conceptual structures cause different sets of alternatives. We next consider these two mechanisms in turn.
3.1 Distance-minimizing listeners
The members of many semantic domains, such as numbers, colors, or proportions, enter in relations of similarity to each other. For instance, two shades of blue can be closer to each other than either of them is to a shade of red. On the other hand, some semantic domains, such as nationality, football teams, or personal identity, are not usually structured by similarity relations. For instance, it is nonsensical to claim that Billy the Kid is closer, in terms of his identity, to Jesse James than Doc Holliday.3
In many cases, when communication happens in domains structured by similarity, and the listener’s task is to construct a representation of the world state given a description produced by the speaker,4 communicative success is not simply a function of whether the listener’s representation is identical to the true world state. Instead, success is an inverse function of the similarity between the true world state and the listener’s guess. In other words, the closer the listener’s guess to the true world state, the more successful the communication.
This measure of communicative success has several motivations. First, if there are finitely many signals but infinitely many possible observations, the probability that the speaker’s observation coincides with a guess by the listener is 0 (except for at most a finite set of possible observations, such as the extremes of the scale). This is the case of the scale of proportions, which is the focus of this paper. Another example is the scale of heights: if a speaker observes that John has height h and sends a signal that covers an interval [a,b], where a < h < b, the probability that the listener will guess exactly h is 0. Fortunately, often it is not crucial that the speaker’s observation and the listener’s guess coincide, as long as they are similar enough. Moreover, even when perfect communication is in principle possible, distance might still be a convenient way to judge communicative success short of perfect precision if smaller deviations from the true value in the listener’s guess are better than larger deviations. In this case, guesses that are more similar to the true state will be preferable for a listener. Franke (2014) discusses this idea in the context of an RSA model. Moreover, Gardenfors (2004) emphasizes the importance of similarity in structuring the way humans think about the world.
In this perspective, it is sensible for a listener to not simply sample from the set of possible world states given their probability after receiving the message, but rather to minimize the expected distance between their guess and the true world state. For instance, if the speaker utters ‘blue’, the listener might select a shade of blue that is located around the center of the blue category, because a point near the center of the category will have a lower expected distance to the true world state than a point that is around the margin of the category. Previous literature supports this idea that listeners tend to guess the center of a category when communicative success depends on the similarity between true state and listener’s guess, e.g., Jäger et al. (2011) showed that the optimal strategy for such so-called simmax signaling games involves a listener that guesses the central point in the category, and Carcassi et al. (2020) show that this assumption has desirable consequences on the evolution of scalar categories.
Consistently with the previous literature (See Chapter 2 of Carcassi (2020) for an overview), we will assume that communication with quantifiers happens on a semantic domain structured by a distance, namely the scales of proportions and numbers.5 Moreover, we claim that in communication with quantifiers, communicative success is of the graded type presented above. For instance, if 1/2 of the As are B, then the communication is more successful if the listener guesses |A ∩ B|/|A| = 0.6 than if the speaker guesses 0.9. This implies that a rational listener does not guess a proportion after receiving a signal simply by sampling from the posterior over proportions. Rather, the rational listener attempts to minimize the expected distance between their guess and the true state of the world.
The listener’s tendency to guess a state that minimizes the expected distance to the speaker’s observation, when in a scalar semantic domain, is not only a result about rational agents, but also aligns with the way we use quantifiers in practice. For instance, imagine receiving the signal ‘between 50 and 100’, and creating a representation of the world state. Even within the part of the scale of integers covered by the expression—e.g. numbers between 50 and 100—the guess does not happen uniformly. Rather, we intuitively tend to guess an integer around the center of the category, i.e., around 75. In other words, we are less likely to select a number close to the category boundaries, such as 99. As we discuss in more detail below, the situation is subtler when multiple possible utterances are involved.
3.2 The structural account of alternatives
In this paper, we point to the structural account of conceptual alternatives (Chemla 2007; Buccola et al. 2012) to explain why ‘most’ and ‘more than half’ have different sets of alternative utterances. To understand the conceptual account of alternatives it is useful to start with its predecessor, the structural account of alternatives (Katzir 2007; Fox & Katzir 2011; Trinh & Haida 2015). The structural account was initially proposed by Katzir (2007) to solve the symmetry problem of Gricean pragmatics (see e.g. Breheny et al. (2018) for an overview of the symmetry problem). One instance of the problem goes as follows. According to classic Gricean pragmatics, ‘some’ implicates ‘not all’ because if ‘all’ had been true, the speaker would have chosen to utter ‘all’ instead of ‘some’. This reasoning relies on the assumption that the live alternatives are ‘some’ and ‘all’. However, a symmetric line of reasoning arrives at the conclusion that ‘some’ implicates ‘all’. If ‘some but not all’ had been true, the speaker would have uttered ‘some but not all’ rather than ‘some’. Therefore, an utterance of bare ‘some’ implicates that ‘some but not all’ is false, i.e., ‘not some or all’ is true. Therefore, under the assumption that the speaker is truthful and can decide to utter ‘some but not all’, ‘some’ ought to implicate ‘all’. This contradicts the fact that ‘some’ implicates ‘not all’ rather than ‘all’. A solution to this puzzle is to break the symmetry between ‘all’ and ‘some but not all’, by excluding the latter from the set of alternatives to ‘some’. The structural account of alternatives achieves this by restricting the set of alternatives to ‘some’ to only those utterances that have a structure at most as complex as ‘some’, thus including ‘all’ while excluding ‘some but not all’.
Formally, the structural theory of alternatives starts with the idea of a structural alternative. ψ is a structural alternative to ϕ (ψ ≲ ϕ) iff ψ is structurally at most as complex as ϕ, i.e., ψ can be obtained from ϕ through a “finite series of deletions, contractions, and replacements of constituents of ϕ” with constituents of the same category taken from the lexicon (Katzir 2007). The core idea is to define the set Astr(ϕ) of utterances alternative to ϕ as follows:
| (5) | Astr(ϕ) = {ψ|ψ ≲ ϕ } |
In words, the set of utterances that enter in the calculation of implicatures for ϕ is the set of utterances that are structurally at most as complex as ϕ.
While the original criterion for alternatives in Katzir (2007) is syntactic, there is emerging theoretical and experimental evidence that the generation of alternatives does not depend on the syntactic structure, but rather on the conceptual structure of utterances (Chemla 2007; Buccola et al. 2021). In particular, Buccola et al. (2021) provides several arguments in favour of the claim that conceptual rather than semantic structure determines pragmatic alternatives. In the interest of space, we only report two and refer the interested reader to the original paper. First, consider the following example:
| (i) | Every dadi called [ hisi daughter ]j or herj dog. |
Which implicates the negation of:
| (ii) | Every dadi called hisi daughter. |
| (iii) | Every dadi called hisi daughter’s dog. |
In the syntactic approach to alternatives construction discussed above, (i) might generate the following alternatives:
| (iv) | Every dadi called hisi daughter. |
| (v) | Every dadi called herj dog. |
While (iv) is a correct prediction (See (ii)), it is not prima facie clear whether (v) is meaningful. Moreover, even under further assumptions that make (v) meaningful it is hard to see how the negation of (iii) can be derived.
The second argument favouring the conceptual account of structural alternatives is that some alternatives might be inexpressible in a language. As an example, consider the English sentence:
| (vi) | John broke all of his arms. |
which arguably sounds odd because it is in competition with the sentence:
| (vii) | John broke both of his arms. |
However, the French counterpart to (vi) sounds as odd as its English version:
| (viii) | Jean c’est cassé tout les bras. |
despite the lack in French of a word for ‘both’. A natural explanation for this is that alternatives are conceptual rather than strictly linguistic, and since the concept of ‘both’ is available even when a word for it is lacking, French speakers derive it as an alternative.
In this paper, we will assume the conceptual rather than the syntactic criterion for alternatives generation. This allows ‘more than half’ (and not only ‘more than one half’) to have e.g., ‘more than three quarters’ as an alternative. Therefore, in what follows, we limit ourselves to applying the basic idea in Equation 5 to conceptual structure rather than syntactic structure.6
We make three crucial assumptions about the way alternatives are generated for the expressions under consideration. First, not every expression of the form ‘a b’ is considered (where a is a cardinal number (e.g. ‘three’) and b an ordinal number (e.g. ‘fourth’) such that a ≤ b). If every a and b were considered, the set of alternatives to ‘one half’ would be the set of rational numbers in the unit interval, e.g., ‘seventeen nineteenth’. Various factors plausibly restrict the set of considered numbers. First, the listener can generally assume that the speaker has a noisy measurement of the true proportion and therefore only produces utterances implying at most a certain level of granularity.7 Second, the communicative aims generally do not require the transmission of precise proportions. Lastly, being an alternative is a graded phenomenon that arguably depends on the complexity of the concept, and more complex concepts are less entertained as alternatives (Buccola et al. 2021). This could explain why ‘five sixths’ does not seem to be an alternative of simpler fractions such as ‘two thirds’; the difference would depend on the different conceptual complexity of the involved numbers.
In what follows, we illustrate the model with the fractions obtained with numbers up to 3 and consider numbers up to 4 when fitting experimental data in Section 7. We chose numbers up to 4 based on previous literature suggesting that they are cognitively simple. First, they are the numbers within the subitizing range, namely that range of numbers that can be evaluated rapidly and confidently (Dehaene 1999). Second, they are acquired earlier than other numbers (Sarnecka & Lee 2009).
The second assumption we make is that the quantifiers constructed by substitution satisfy the properties of conservativity, extensionality, and isomorphism-closure invariance discussed in Peters & Westerståhl (2006). These are universal properties of the meaning of simple determiners, and it is plausible that there are mechanisms preventing them from being considered. Intuitively, these properties imply that the only sets relevant to the verification of the alternatives are |A – B| and A ∩ B.
The third assumption we make is that the concepts expressed by ‘most’ and ‘more than half’ are structured in way proposed by Hackl (2009) (see Equations 1 and 2). Crucially, the conceptual structure of ‘more than half’ contains a fraction 1/2, the numerator and denominator of which can be substituted with other simple integers. Therefore, the main consequence of this assumption is that ‘two thirds’ and structurally equivalent expressions are alternatives to ‘half’ according to the criterion in Equation 5, while ‘most’, which lacks the fraction in its conceptual structure, has a smaller set of conceptual alternatives.8 Under the two assumptions just discussed, the criterion defined in Equation 5 has the correct consequences for the cases at hand. Namely, Astr(‘most’) contains ‘all’ and does not contain ‘more than three quarters’. On the other hand, Astr(‘(one) half’) contains e.g. ‘three quarters’.
3.3 The joint effect of the two mechanisms
In this section, we have presented two mechanisms that play a role in the way quantifiers are interpreted. These two mechanisms have already been discussed in the literature in other contexts (Franke 2014; Jäger et al. 2011; Katzir 2007). The main contribution of this paper is, therefore, to show how these two mechanisms can explain the difference in the proportions typically conveyed by ‘most’ and ‘more than half’. In particular, our account does not need to introduce a difference in scale structure presented in Solt (2016). Before we turn to a computational model of our account, we give an intuitive sense of how it works.
Our model is in the Rational Speech Act (RSA) modelling framework (Scontras et al. 2021). This framework typically models language users—speakers and listeners—thinking recursively about each other’s minds with the aim of producing and interpreting utterances. In our case, we model a pragmatic speaker S2 who selects a signal that is most useful to a pragmatic listener L1. In the standard RSA model, no matter what signal L1 receives, they always interpret it on the background of a fixed set of alternative signals. In contrast, in our model the utterance produced by S2 also determines the set of alternatives considered by L1 in their pragmatic reasoning, in the way described by the conceptual account of alternatives discussed above.
In the case at hand, S2 selects ‘most’ or ‘more than half’ not simply as a function of their extension on the scale of proportions, but instead also implicitly selecting the set of alternatives that will allow a pragmatic listener to choose a proportion that is as close as possible to the speaker’s observation. Since pragmatic listener L1 guesses points closer to 0.5 for a rich alternative set such as the one induced by ‘more than half’, the speaker selects ‘more than half’ for such proportions. On the other hand, since the listener will guess points higher on the scale of proportions for ‘most’, the speaker produces ‘most’ for such proportions. As a consequence, the speaker chooses ‘more than half’ to describe points close to 0.5 and ‘most’ for points higher on the scale.
4 An RSA model of the two mechanisms
In the previous section, we have informally introduced two mechanisms in the interpretation of quantifiers. In this section, we propose a formal implementation of these two mechanisms in the RSA modelling framework before turning to the specific case of ‘most’ and ‘more than half’ in Section 5.
4.1 Basic RSA model
The RSA framework is meant to model the process of recursive mindreading that lies behind the pragmatic interpretation and production of utterances (See for instance Goodman & Stuhlmüller (2013); Franke (2014); Frank (2017), and Scontras et al. (2021) for a textbook introduction). RSA models usually start with a pragmatic listener who interprets utterances based on the simulated behaviour of a pragmatic speaker. Given an observation, the pragmatic speaker in turn tends to choose the most useful utterance for a literal listener. Finally, the literal listener interprets utterances based solely on their literal meaning. We will first explain the simplest type of RSA model and then a modification that will be useful to model quantifiers.
The simplest RSA model starts with a set of utterances u and a set of possible states s. The meaning of each utterance can be encoded as the set of those states that verify the utterance. The pragmatic listener L1 receives an utterance u and calculates a posterior over states by Bayesian update, combining their prior over states with the probability that the pragmatic speaker S1 would have produced the utterance given each state:
| (6) | 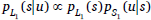 |
The pragmatic speaker, in turn, observes a state and produces an utterance that tends to maximize the utility U (u; s) for a literal listener L0 given the state:
| (7) | 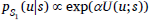 |
The utility U (u; s) is the negative surprisal of the state s given the utterance u minus the cost of utterance u, so that the speaker favours utterances that make the state less surprising for the literal listener while minimizing the utterance cost c(u):
| (8) | 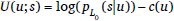 |
Finally, the probability that the literal listener L0 attributes to each state given an utterance is simply 0 if the state does not verify the utterance, and proportional to the prior for the state otherwise:
| (9) | 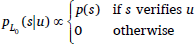 |
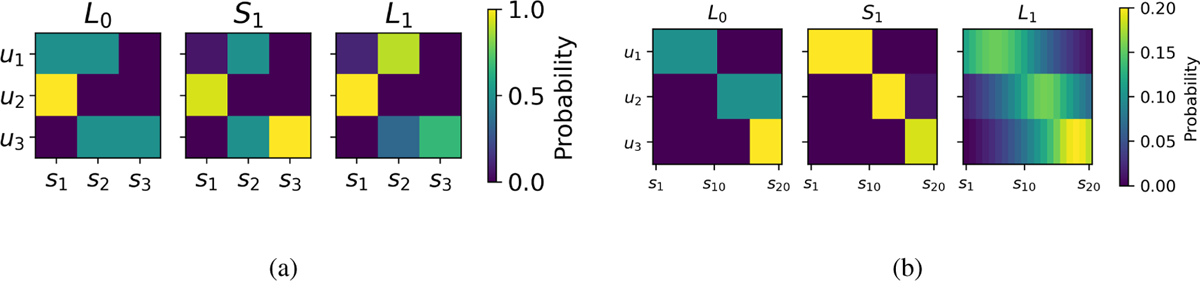
Figure 1(a) shows L0, S1, and L1 in this simple RSA model. The crucial phenomenon that can be observed in Figure 1(a) is that L1 calculates a scalar implicature: although utterance u1 is, in its literal sense, compatible with both s1 and s2, S1 tends to produce u1 mostly for s2, because when s1 is observed S1 tends to use the more useful signal u1. Therefore, when hearing u1 L1 is more likely to guess s2.
(a) Simple RSA model with three possible utterances u (y-axis) and three states s (x-axis). L1 calculates a scalar implicature for utterances u1 and u2 (α = 4). The left, central, and right plots correspond to L0, S1, and L1 respectively. Note that the color indicates the probability of guessing a state given a signal for L0 and L1, and the probability of producing a signal given a state for S1. (b) RSA model with a distance-minimizing L1. The model displayed in the plot uses a language with three utterances and 20 states. The listener L1 does not simply guess the signal observed by the speaker by sampling their posterior, but rather attempt to minimize the expected distance between their guess and the speaker’s observation (α = 4, ρ = 0.1). See Figure 2(a) for more detail.
4.2 Distance based listeners
In the simple RSA models above, success in communication is binary, solely a function of whether the listener’s guess coincides with the speaker’s observed state. This is plausible in cases where the set of states has no internal structure. However, as discussed above, in the case where a notion of distance is well-defined on the set of states, the listener might not be simply trying to guess the speaker’s observation but rather might strive to minimize the (expected) distance between the state they select and the speaker’s observation.9
To model the effects of a well-defined distance D on the set of states, we modify the listener L1 so that instead of selecting a state by sampling from their posterior distribution given the signal, they try to minimize the expected distance between their selection s and the true state. Therefore, we define the choice probability for listeners as follows:10
| (10) | 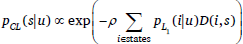 |
where ρ is the parameter of a softmax function which determines how strongly the listener tends to minimize the expected distance and 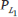 is defined as above in Equation 6. The listener described in Equation 10 tends therefore to minimize the expected linear distance function. Figure 1(b) shows the effects of this modification of the model for 20 states and with linear distance D(sn, sm) = |n–m|. The right plot shows that in this modified RSA model, L1 tends to guess points located centrally in the category, after the category has been restricted by scalar implicature.
is defined as above in Equation 6. The listener described in Equation 10 tends therefore to minimize the expected linear distance function. Figure 1(b) shows the effects of this modification of the model for 20 states and with linear distance D(sn, sm) = |n–m|. The right plot shows that in this modified RSA model, L1 tends to guess points located centrally in the category, after the category has been restricted by scalar implicature.
4.3 Varying sets of alternatives
The modification to the basic RSA model above is an implementation of the first mechanism discussed in Section 3. The second mechanism concerns the way that the comparison set depends on the speaker’s utterance.
In the basic RSA framework, the set of possible utterances considered by the pragmatic speaker and the pragmatic listener are identical. However, according to the structural account of alternatives discussed above, the set of utterances considered by the listener depends on the utterance they receive. For instance, if the speaker utters ‘101’, the listener will consider all alternative utterances at most at a similar level of granularity as 101, such as 91 and 100. However, if the speaker utters ‘100’, the listener in the model considers an alternatives set containing, e.g., only 90 and 100, but not 101.
To model this, we introduce a speaker S2. S2, much like S1, tends to select the signal that minimizes the listener’s surprise for the real state given the signal. However, the set of alternative utterances considered by L1 is not independent of the signal received by L1. Instead, the set of alternative utterances considered by L1 (and therefore by the lower levels S1 and L0) depends on the utterance L1 receives. S2 takes this into account when selecting an utterance, calculating for each utterance the utility of the utterance given the set of alternatives that L1 considers when receiving that utterance. So, while L1 does not reason about S2, S2 does not select an utterance alone, but in addition also the set of alternatives that come with the utterance.
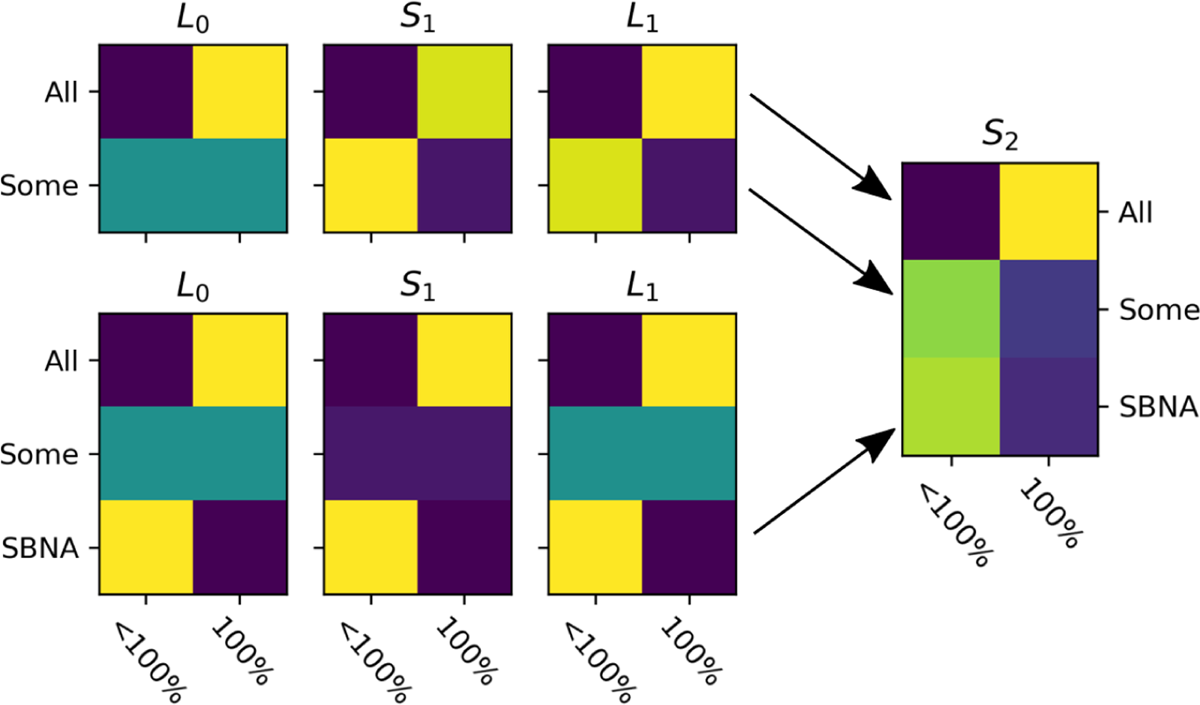
Consider now for illustration the case of ‘some’, ‘all’, and ‘some but not all’ discussed above. Figure 2 shows the reasoning of speaker S2 as they decide which signal to produce given that they observed a 100% state or a state < 100% (and > 0%). Being a rational speaker, S2 produces signals that maximize the probability that L1 attributes to the true state. Since L1 is a rational listener, the probability attributed to each state given a signal depends on the set of alternatives to that signal. According to the structural account of alternatives, the set of alternatives is a function of the received signal. So if S2 sends ‘some but not all’ (SBNA), L1 will run pragmatic reasoning on the set of utterances {‘All’, ‘Some’, SBNA} (bottom row of plots in Figure 2. Note that in this set of alternatives, corresponding to the symmetric case of the symmetry problem, ‘some’ does not implicate SBNA. On the other hand, if S2 utters ‘some’, L1 will reason only with {‘All’, ‘Some’} according to the structural account of alternatives, and therefore calculate the implicature from ‘some’ to SBNA (top row of plots in Figure 2). In sum, given a state S2 will tend to produce the utterance that is most useful for a hypothetical L1 who reasons about a set of alternatives which itself depends on S2’s utterance.
Structural account of alternatives with the simple example of ‘all’, ‘some’, and ‘some but not all’ (SBNA). Since 0% would be black in all plots, it is implicitly excluded from the scale for ease of visualization. Lighter colors indicate higher probability. After receiving an utterance u, L1 constructs a set of conceptual alternatives specific to u. For instance, upon hearing ‘all’, L1 runs pragmatic inference with the set of conceptual alternatives {all, some}, which does not include ‘some but not all’. Therefore, for each utterance u S2 calculates the utility of u for L1 relativized to u’s comparison set as calculated by L1, rather than considering a fixed set of alternatives. For visualization purposes, ‘all’ and ‘some’ as considered by S2 are represented together in the top row as they share the same set of alternatives.
This picture of alternatives is, in many respects, a simplification. For instance, it is likely that the listener is uncertain about which set of alternatives ought to be considered in the context. More complex discussions of issues related to granularity and alternatives can be found in the literature, see e.g. Bastiaanse (2011) and Carcassi & Szymanik (Forthcoming) for numerals. However, these more complex models are not needed to explain the issue at hand, and therefore we leave the investigation of the subtleties to future work.
In sum, the model presented in this section will apply whenever (1) the listener is trying to minimise the distance between their guess and the speaker’s observation, and (2) different terms induce different sets of alternatives. Crucially, the model applies even if two expressions with different sets of alternatives are truth-conditionally equivalent.
In this section, we have formalized the two mechanisms discussed in Section 3 within the RSA framework. The resulting model is summarized in natural language in Figure 3. In the resulting model, structurally different expressions induce the pragmatic listener to consider different sets of alternative utterances. Moreover, the listener does not simply guess uniformly from the enriched part of the parameter space but rather tends to guess points that are central in the pragmatically enriched category. Therefore, even intensionally equivalent expressions will be used differently, as long as they are structurally different. The next section shows how this model applies to the specific case of the contrast between ‘most’ and ‘more than half’.
Structure of RSA model with distance-minimizing listener and structural account of conceptual alternatives. The set of alternative utterances considered by L1 is not fixed but depends on the received utterance. Moreover, L0 and L1 do not simply guess a state based on their posterior probability given the received signal but rather tend to guess a state that is expected to be close to the speaker’s observation.
5 An RSA model for ‘most’ vs ‘most than half’
In what follows, we will model communication with quantifiers by applying the RSA model described above to the following simple referential communication task, modelled after Pezzelle et al. (2018) where communication was set up similarly in a production task. A speaker observes two sets, A and B, and attempts to communicate to a listener which proportion of A is also in B in the way modelled by the modified RSA model introduced above.
The set of possible meanings includes Aristotelian quantifiers ‘all’, ‘none’, and ‘some’, and some minimal set of alternatives for ‘more than half’ (Table 1). Note that the meanings of the three Aristotelian quantifiers we include can be obtained by exchanging >, ≥, <, and ≤ with each other, and A ∩ B, A, and A – B with each other. The literal meaning of each quantifier in the model corresponds to a portion of the scale of proportions. The set of structural alternatives to ‘more than half’ is closed under substitution of ‘more’ by ‘less’, and by (semantically meaningful) substitutions of one, two, and three (both their cardinal and ordinal versions) with each other.
Meaning of each signal in the model. MT=’more than’, LT=’less than’.
| Utterance | Structure | Extension |
|---|---|---|
| All (∀) | |A ∩ B| ≥ |A| | {1} |
| Most | |A ∩ B| > |A – B| | (1/2, 1] |
| None (¬∃) | |A – B| ≥ |A| | {0} |
| Some (∃) | |A|>|A – B| | (0, 1] |
| MT a half (> 1/2) | |A ∩ B| > |A| | (1/2, 1] |
| MT one third (> 1/3) | |A ∩ B| > |A| | (1/3, 1] |
| MT two thirds (> 2/3) | |A ∩ B| > |A| | (2/3, 1] |
| LT a half (< 1/2) | |A ∩ B| < |A| | [0, 1/2) |
| LT one third (< 1/3) | |A ∩ B| < |A| | [0, 1/3) |
| LT two thirds (< 2/3) | |A ∩ B| < |A| | [0, 2/3) |
We make two additional assumptions about the set of meanings. First, we exclude the meaning expressed by ‘not all’, namely |A| > |A ∩ B|. A morphologically simple expression for ‘not all’ is cross-linguistically unattested, indicating that for reasons presently not fully understood it might not be a valid conceptual alternative (Horn 1989). In this, we follow Buccola et al. (2021), who argue that the meaning expressed by ‘not all’ is conceptually more complex than those of the other Aristotelian quantifiers. See Carcassi & Sbardolini (2021) for a recent proposal where a more sophisticated language of thought explains a related universal in the domain of Boolean connectives. Second, we exclude non-conservative quantifiers obtained by adding B to the substitution source. These are also cross-linguistically unattested (Barwise & Cooper 1981; Szymanik 2016).11
As in the modified RSA model presented above, the alternatives considered by the pragmatic listener depend on the speaker’s utterance. For instance, if the speaker uttered ‘some’ the listener would consider a set of alternatives containing ‘all’ but not ‘more than two thirds’, while if the speaker uttered ‘more than one third’ both ‘all’ and ‘more than two thirds’ would be possible options for the listener. In the present case, the utterances above can be divided in two groups, the first containing ‘all’, ‘most’, ‘none’, and ‘some’, and the second containing the remaining utterances. Each utterance in the first group contains all other utterances in that group as alternatives, and none of the utterances in the second group. Each of the utterances in the second group contains all utterances in its set of alternatives.12
To isolate the effects of the account of alternatives discussed above from the consequences of utterance cost, we assume that signals have no cost. Moreover, to keep the results as simple as possible S2 can only produce ‘all’, ‘most’, ‘none’, ‘some’, ‘more than a half’, and ‘less than a half’, rather than the full set of alternatives in Table 1. For the speaker to be able to calculate a distribution over utterances given any state, there has to be at least one utterance to refer to each state in each set of alternative utterances.
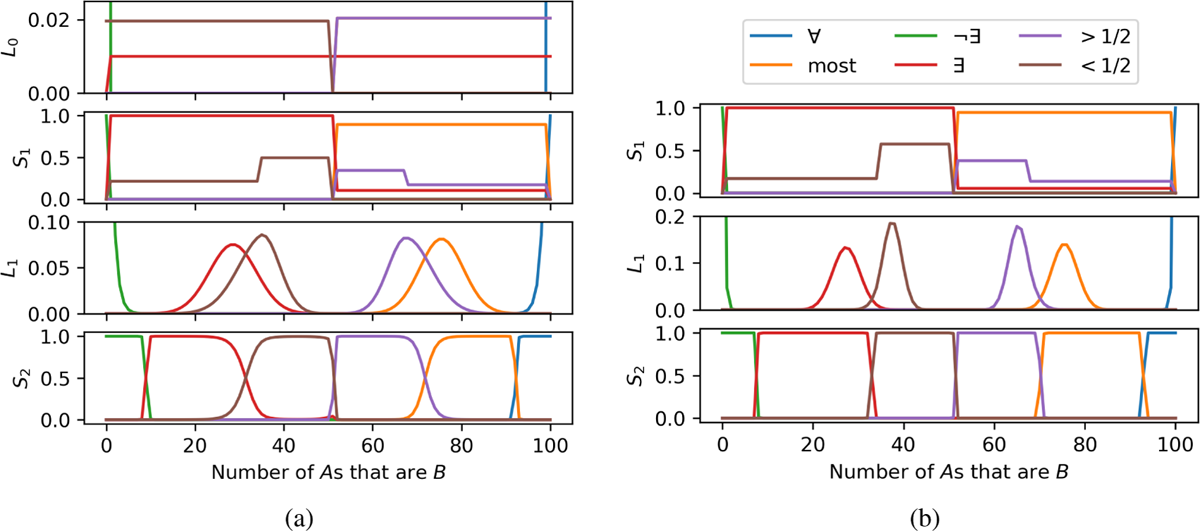
The results of the model are shown in Figure 4(a). L0 guesses uniformly within the categories expressed by each signal considered by S2. L0 treats ‘most’ and ‘more than half’ identically, guessing uniformly among the states between 51 and 100. Finally, S0 selects the maximum for ‘every’ and the minimum for ‘none’.
(a) The plots shows the results with |A| = 100, α = 3 and ρ = 1. Each plot shows the behaviour of a different agent in the RSA model. Note that while the lines for L0, S1, and L1 are shown on the same plot, they implicitly have different comparison sets. (b) The plots shows the results with |A| = 100, α = 4 and ρ = 3. L0 is not shown as it is identical to Figure 4(a).
With S1, the set of alternatives for each signal matters (second plot from top in Figure 4(a)). More specifically, while the lower bound for both ‘most’ and ‘more than half’ are similar for S1, their upper bounds are different as a consequence of the different ways that the respective set of alternatives cover the scale. ‘More than half’ implicates less than two thirds, and therefore tends not to be used for proportions higher than two thirds, while most only implicates ‘not all’. Note that while the six signals are plotted together in Figure 4(a), the distribution for each signal is computed independently with a possibly different set of alternatives utterances. Therefore, S1 does not suffice to explain the difference between ‘most’ and ‘more than half’.
L1 tends to pick the central point in the categories as produced by S1 (third plot from the top in Figure 4(a)). Therefore, L1 tends to guess points closer to the middle of the scale for ‘more than half’ than for ‘most’, because the former is produced by S1 for a range of proportions closer to the scale’s midpoint. Finally, the pragmatic speaker S2 tends to pick ‘more than half’ for signals closer to the midpoint of the scale than ‘most’ (bottom plot in Figure 4(a)).
The results in Figure 4(a), while qualitatively correct, are quantitatively surprising in that the upper bound of ‘more than half’ goes higher than in the data presented by Solt (2016). However, the positions of the involved bounds are sensitive to the parameter values. For instance, Figure 4(b) shows a parameter setting that makes predictions closer to Solt’s data. Moreover, as more proportions are included in the set of alternatives to ‘more than half’, the alternatives will divide the scale with a higher granularity, moving the upper bound of ‘more than half’ strictly closer to 50%.
6 Experiment
In the previous sections, we explained the difference in the typical proportions conveyed by ‘most’ and ‘more than half’. We implemented the proposed account in an RSA production model and showed that this model can qualitatively produce the observed effect. This section presents the results of a quantifier production experiment and analyses how well the RSA can fit them quantitatively.
6.1 Task
The experiment is based on the ‘grounded task’ in Pezzelle et al. (2018) with a slightly different set of quantifiers. The original experiment was conducted in Italian, whereas our experiment was in English. The data was gathered on the Prolific13 platform and successfully obtained for 57 participants (43 females, 14 males), while 8 participants were excluded as they did not finish the experiment. 340 judgments were obtained for each participant, for a total of (340*57=) 19380 data points. The experiment was coded in PsychoPy 3.2.4 (Peirce et al. 2019). Since the experiment is described in detail in Pezzelle et al. (2018), we only report here the main design choices.
Each participant completed 340 rounds, each round consisting of three screens. The first screen, which lasted 500ms, only contained a fixation cross. The second screen, which lasted one second, showed objects arranged in a grid, with possibly empty slots. The objects were a mixture of one type of animal and one type of artifact, the exact types varying across pictures. Each image contained between 3 and 20 (inclusive) objects. Finally, the third screen showed a grid of nine quantifiers: ‘most’, ‘more than half’, ‘all’, ‘half’, ‘many’, ‘none’, ‘less than half’, ‘few’, ‘some’ (the choice of quantifiers is the only difference in design to Pezzelle et al. (2018). The participant then selected exactly one of the quantifiers in the grid. The quantifiers were not presented in a sentence context but instead at the start of the experiments two screens instructed the participants always to select the quantifier which best answered the question “How many of the objects are animals?”.
6.2 Results and discussion
Table 2 reports summary statistics for each quantifier, aggregated across all participants. The results are comparable to Table 1 of Pezzelle et al. (2018). The order is the same for those quantifiers that appeared both in Pezzelle et al. (2018) and in our experiment, namely ‘None’ < ‘Few’ < ‘Some’ < ‘Many’ < ‘Most’ < ‘All’. The percentages for which ‘None’ and ‘All’ were used are less extreme in our results (respectively 0.06 and 0.95) than in Pezzelle et al. (2018) (respectively 0.01 and 0.99). Likely, the reason for this difference is that our production data is noisier, because for reasons explained below we did not exclude any participant from the experiment. The proportions are close for the remaining quantifiers, especially ‘Few’ (0.23 in our vs 0.26 in Pezzelle et al. (2018) and ‘Many’ (0.7 vs 0.64). In the case of ‘Some’ (0.37 vs 0.44), the average in our experiment is lower, indicating that ‘almost none’ in Pezzelle et al. (2018) moved ‘Some’ higher. Similarly, ‘Most’ (0.77 vs 0.69) is higher in our data, indicating that ‘almost all’ in Pezzelle et al. (2018) moved ‘Most’ lower.
Descriptive statistics for each signal in the experiment. This table matches Table 1 in Pezzelle et al. (2018). Values in brackets refer to SD. Columns refer to (a) the total number of responses for each quantifier, (b) the average proportion of animals out of the total number of objects, (c) the average number of targets, (d) the average number of non-targets, (e) the average total number of items.
| (a) resp | (b) % targ | (c) n targ | (d) n non-targ | (e) n total | |
|---|---|---|---|---|---|
| None | 1186 | 0.06 (0.2) | 0.65 (2.53) | 10.88 (5.27) | 11.53 (4.92) |
| Few | 3784 | 0.23 (0.14) | 2.41 (1.75) | 9.2 (5.0) | 11.62 (5.46) |
| Less than half | 2647 | 0.36 (0.13) | 4.2 (2.35) | 7.72 (4.0) | 11.92 (5.12) |
| Some | 1459 | 0.37 (0.19) | 4.56 (2.79) | 8.5 (4.56) | 13.06 (5.07) |
| Half | 1421 | 0.49 (0.1) | 5.69 (2.7) | 5.97 (2.92) | 11.67 (4.96) |
| More than half | 2762 | 0.63 (0.13) | 7.27 (3.82) | 4.13 (2.48) | 11.4 (5.0) |
| Many | 1449 | 0.7 (0.17) | 9.82 (4.24) | 4.22 (2.87) | 14.04 (4.66) |
| Most | 3517 | 0.77 (0.14) | 9.67 (4.81) | 2.81 (2.28) | 12.48 (5.43) |
| All | 1155 | 0.95 (0.19) | 10.92 (5.33) | 0.6 (2.6) | 11.52 (5.02) |
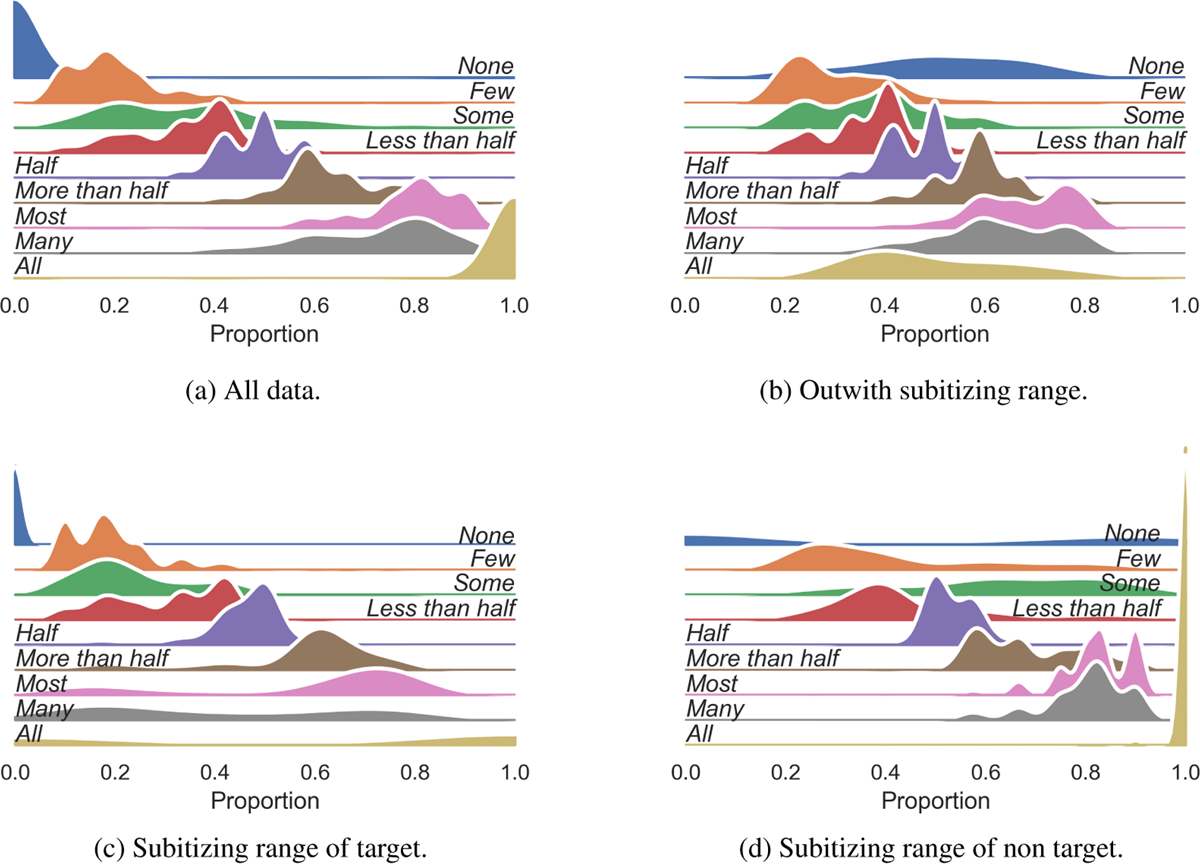
Figure 5 shows the distribution of each quantifier aggregated across participants. Figure 5(a) shows the results for all participants, which as discussed above are similar to Pezzelle et al. (2018). Figure 5(b) shows the aggregated data with more than 3 animals and more than 3 artifacts. The distributions for the signals in 5(b) is close to 5(a), except for ‘None’ and ‘All’, which shows random behaviour. This is expected, as the data in 5(b) excludes all the stimuli where ‘None’ and ‘All’ apply and therefore production of those signals comes from noise. Figure 5(c) shows the data with fewer than 4 targets (animals). While ‘None’ is produced correctly, ‘All’ is as expected noisy. A similar effect, although to a smaller degree, is seen for ‘Many’ and ‘Most’. In Figure 5(d), the reversed pattern is seen for ‘None’, which is as expected noisy, and to a lesser extent for ‘Some’. Overall, our results are similar to the results in Pezzelle et al. (2018) for the signals shared by the two experiments.
Kernel density estimation of data aggregated across participants for various subsets of the data. (a) All data. (b) Data where both the number of targets (animals) in the picture nor the number of non-targets (artifacts) was greater than 3. (c) Data with 3 or fewer target objects (animals). Y-axis for ‘None’ is scaled down for visualization purposes. (d) Data with 3 or fewer non-target objects (artifacts).
The quantifiers which were not in Pezzelle et al. (2018) show the expected behaviour. ‘Few’ is lower than ‘Less than half’, and they are respectively close to ‘Almost none’ and ‘The smaller part’ in Pezzelle et al. (2018). ‘Half’ is, as expected, centered around the midpoint of the scale.
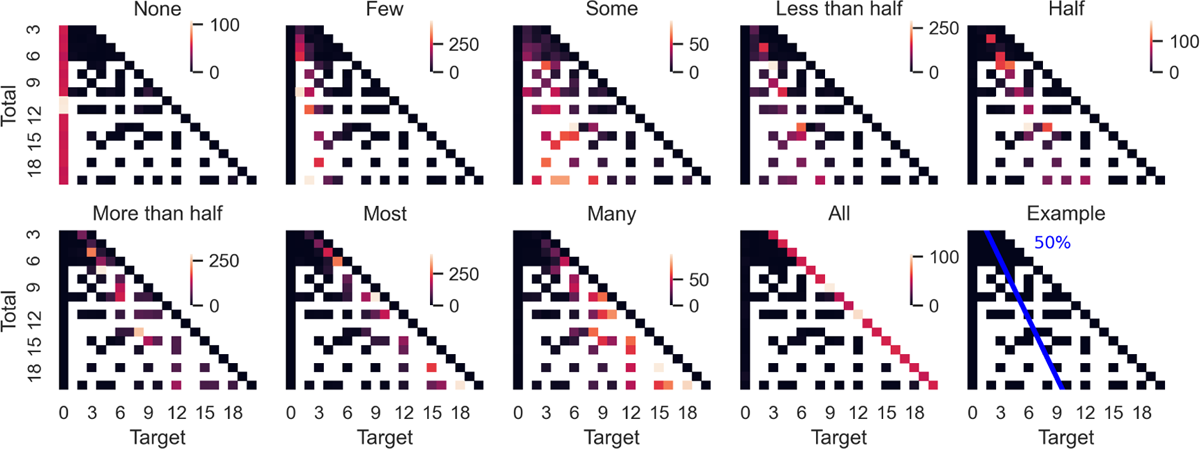
Figure 6 shows the number of times each quantifier was used for each stimulus, aggregated across participants. The y-axis of the figure represents the total number of objects, the x-axis the number of target objects. This way of representing quantifiers in a triangle originates from van Benthem (van Benthem 1986; 1987). A cardinal quantifier used to express ‘between a and b’ (with a,b ∈ ) would appear in the plot as a group of light squares between the vertical lines Target = a and Target = b. On the other hand, a proportional quantifiers used to express ‘between a and b (with a,b ∈ [0,1]) appears as a group of red squares between the lines Target = a × Total and Target = b × Total. All the quantifiers’ lower and upper bounds are roughly straight lines in the plot. This shows that the quantifiers were interpreted proportionally, i.e., did not depend on the absolute number of objects on the screen but only on the proportion between the total number and the number of target objects. This is important mainly in the case of ‘Few’ and ‘Many’, which have been argued to be ambiguous between a cardinal and a proportional interpretation.
Graded van Benthem triangle. The plot shows, for each combination of total number of objects (targets + non-targets) and number of target objects, the counts of usages of each quantifier aggregated across participants. The completely white squares are combinations that none of the participants saw. The black squares are observations for which the quantifier was never produced, and squares become lighter with increasing number of uses. A specific proportion can be imagined as a straight line starting from (0,0) (outside of each plot). The bottom right plot is an illustration of the proportion 0.5. As expected for proportional quantifiers, the upper and lower bounds for each quantifier roughly follow straight lines with various inclinations.
The crucial result is that the difference between ‘most’ and ‘more than half’ observed by Solt (2016) in the corpus is reproduced in our experiment. More precisely, three of Solt (2016)’s predictions were verified. First, the approximate lower bound of ‘More than half’ is right above 0.5, as observed by Solt (2016). Second, the upper bound of ‘More than half’ roughly corresponds to the lower bound of ‘Most’. Third, the upper bound of ‘Most’ is close to 100%. However, the upper bound of ‘More than half’ is higher than the one observed by Solt (2016) in the corpus. We return to this point in more detail below.
7 Model fitting
7.1 An intuitive summary
In the model-based approach to statistics we use in this section, a model of the situation is given that, based on unobserved parameter values and prior distributions over them, predicts the probability of each possible observation. Bayes theorem, plus various approximation algorithms, is then used to go from the observed data to a posterior distribution over the unobserved variables. Multiple models can then be compared in terms of how well they are supported by the data.
In our case, each data point consists of three observations: the total number of objects seen by the participant, the number of animals, and the quantifier chosen by the participant. We assume that the participant chooses a quantifier based on the RSA described in Section 5, extended with the signals in Table 3, using α and ρ parameters specific to that participant. We also attribute to each participant a noise parameter that regulates how noisy their production behaviour is. In each trial, the participant observes the total number of objects and the number of animals, then calculates the probability of producing each quantifier, disturbs it with noise, and finally selects a specific quantifier we can observe.
Meaning of signals added to the ones in Table 1 for the experimental data fitting. MT=’more than’, LT=’less than’.
| Utterance | Structure | Extension |
|---|---|---|
| Half (1/2) | |A ∩ B| = |A – B| | {0.5} (but see Appendix A) |
| Many | |A ∩ B| > d|A| | (0.4, 1] (with d = 0.4) |
| Few (¬∃) | |A – B| < d|A| | [0, 0.2) (with d = 0.2) |
| MT one fourth (> 1/4) | |A ∩ B| > |A| | (1/4, 1] |
| MT three fourths (> 3/4) | |A ∩ B| > |A| | (3/4, 1] |
| LT one fourth (< 1/4) | |A ∩ B| < |A| | [0, 1/4) |
| LT three fourths (< 3/4) | |A ∩ B| < |A| | [0, 3/4) |
We compare two such RSA models, with and without the structural account of conceptual alternatives (Figure 7). We find that the former is much better supported by the data than the latter. Predictions for a new hypothetical participant (Figure 9) confirm that the model with structural conceptual alternatives is closer to the observed data.
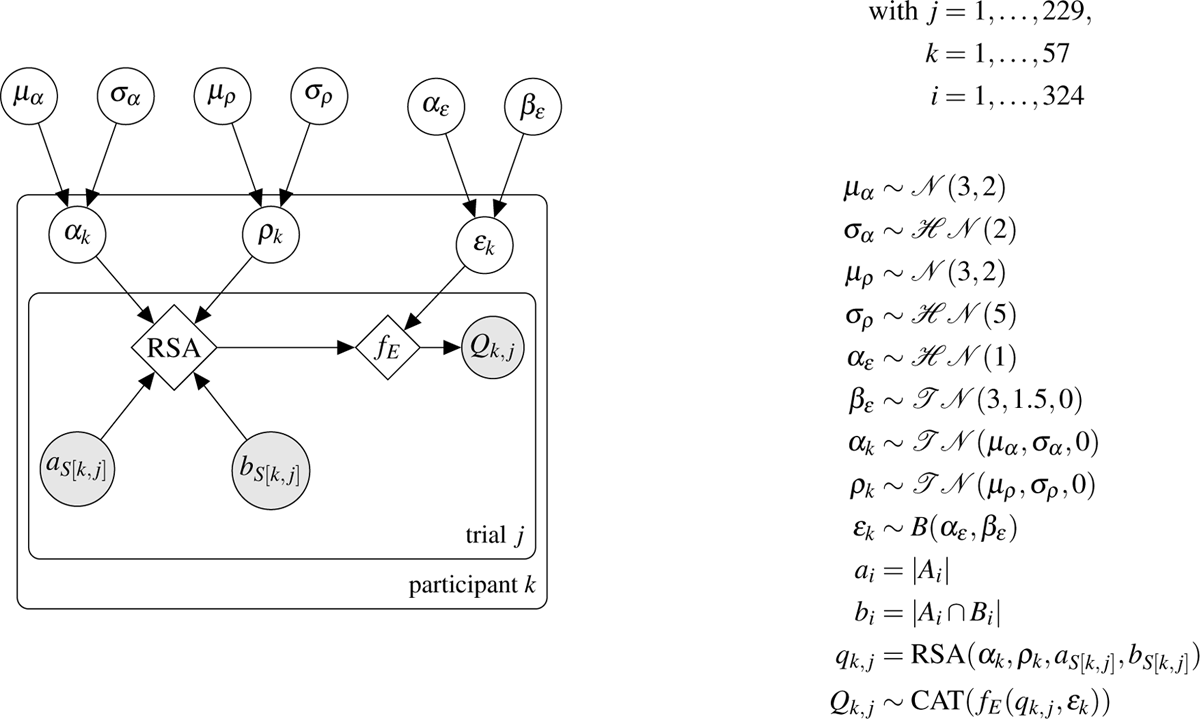
DAG for the Bayesian model. See Section 7.2 for definitions of functions RSA and fE. We use the following parameterizations: the normal distribution takes a mean μ parameter and a σ parameter, the halfnormal distribution only a σ parameter, truncated normal distribution a μ, σ, and lower bound parameters in this order, the beta distribution B parameters α and β in this order, and the categorical distribution a probability vector.
7.2 Extending the production model
The production model presented above consisted of an RSA model with 10 signals, 6 of which could be produced by the speaker and 4 of which were only implicitly considered as alternatives. In order to use the RSA model developed in Section 4 to fit the experimental data, the language has to be slightly enriched to include the signals in the experiment. The signals included in the model are the ones in Table 1 plus the ones in Table 3. In the experimental production model, we include fourths, effectively increasing the granularity of the set of alternatives to ‘more than half’. In our opinion, this makes the model more realistic, but future experimental work can try to directly elicit cognitively plausible alternatives.
While in the model the participants only consider producing the available signals, they imagine a listener who considers a broader range of signals, including some that the participants themselves cannot produce. We assume that the participant is not assuming that the listener knows what signals are available for the participant to produce. For instance, in a similar experiment that only contained ‘some’ and ‘none’, we can imagine that the participant would produce ‘some’ but feel uneasy about the choice upon observing a screen where all the objects were animals. This assumption may fail, but then Solt (2016)’s account cannot explain the observed behaviour either, since ‘more than half’ fails to be upper bounded by ‘more than a third’.
Based on the discussion of conceptual alternatives above, we retain two groups of alternatives as follows: ‘All’, ‘Most’, ‘None’, ‘Some’, ‘Half’, ‘Many’, and ‘Few’ are all alternatives of each other, and do not have any of the other signals as alternatives. The remaining signals are all alternatives of each other and of the signals in the first group. For instance, using the notation of Katzir (2007) introduced in Equation 5, ‘most’/’all’/… ≲ ‘more than half’/’less than three quarters’/…, but ‘more than half’/… ≴ ‘most’/…. This way of structuring the set of alternatives assumes that ‘half’ is analysed as |A ∩ B| = |A – B| rather than |A ∩ B| = | A |, since the latter conceptual structure would imply that the alternatives to ‘half’ include ‘more than half’ etc. However, simulations show that this choice does not have a substantial influence on the resulting production behaviour.
The semantics of quantity words ‘many’ and ‘few’ is currently being debated (Rett 2018). We assume they do not conceptually encode a comparison with precise proportions, which could compete with concepts such as ‘three quarters’. Rather, following previous work (Hackl 2000; Romero 2015), we assume they introduce a comparison with a contextually determined degree d, which we fix to 0.4 in the case of ‘many’ and 0.2 in the case of ‘few’. We leave to future work to more precisely determine the position of the thresholds for these two quantifiers or implement participant-wise estimation of their thresholds from the data. For simplicity, we assume that these two quantity words alternate with all other non-fractional expressions.
In addition to specifying the alternatives set for each quantifier, the model requires a specification of their literal meanings. Most of the quantifiers we included in the experiment have a default interpretation in the literature, and we have discussed the case of ‘few’ and ‘many’. The meaning of ‘half’ is also made non-trivial by the discreteness of the stimuli. We discuss ‘half’ more in detail in Appendix A.
Up to this point, we have considered the production behaviour of a rational RSA agent. However, behaviour of real participants will not perfectly conform to the RSA model. First, there will be systematic error from aspects of quantifier usage that the RSA model does not capture. Second, there will be noise coming from participants pressing the wrong button or not paying attention. To account mainly for the latter kind of error, we add production noise in the model. The production noise introduces a third production noise parameter Ɛ for each participant, in addition to the RSA α and ρ parameters. We give the following generative characterization of production noise. Assume the participant has made an observation and has calculated a posterior distribution over quantifiers given the observation. Then, the participant’s response is sampled from the RSA posterior distribution with probability 1–Ɛ, and sampled from a uniform distribution over quantifiers with probability Ɛ. Therefore, the production noise is a mixture with the RSA distribution and a uniform distribution as components, and Ɛ–1 and Ɛ as the mixture weights, respectively:
1
where is the vector of production probabilities according to the RSA model and is a vector of ones of length 9, i.e. the number of signals in the model. Intuitively, the greater the value of Ɛ the noisier the behaviour of the participant, i.e. the less the participant’s decision depends on the observed state. When Ɛ = 0, the participant’s behaviour is fully determined by the RSA predictions. When Ɛ = 1, the participant selects a completely random quantifier by clicking a random button. In sum, the behaviour of a participant p producing a judgment about a stimulus s is modelled by two functions: an RSA function and a noise function fE. The RSA function takes four parameters: (1) the participant’s alpha parameter αp, (2) the participant’s distance-minimization parameter ρp, (3) a total picture size as, and (4) the number of target objects bs. The output of RSA, RSA (αp, ρp, as, bs), is the input of the error function which calculates the mixture probability of each quantifier fE (RSA (αp, ρp, as, bs), Ɛp). Thus, the probability of the participant producing each quantifier is determined by the output of the error function.
7.3 RSA-based Bayesian models
The hierarchical model (displayed as a Bayesian directed acyclic graph in Figure 7) has three nested levels. The bottom level is the level of specific participants’ judgments for specific stimuli. j is an index ranging over the 57 participants, k is an index ranging over the 229 trials (per participant), and i is an index ranging over the 324 stimuli (i.e., combinations of possible sizes between 3 and 20 for A and A ∩ B). The stimulus shown to participant k at trial j is indicated by S[k,j], where S is a matrix with shape 57 × 229. The bottom level also includes the two properties of a stimulus i relevant to production, namely a vector a with 324 components containing the total number of objects for each stimulus, and a vector b containing the number of target objects. The quantifier Qk,j produced by participant k in trial j is sampled from a categorical distribution with the production probability vector parameter calculated, in the way described in the previous section, as fE (RSA (αk, ρk, aS[k,j], bS[k,j]), Ɛk).
The middle level of the hierarchy is the level of the individual participants k. Three parameters are associated with the participant: the two RSA parameters αk and ρk and the error parameter Ɛk. These three parameters control the predicted behaviour at the bottom level, and are themselves sampled from population-level distributions at the top level.
The top-level is the population level, from which the participant-level parameters are sampled. The top-level contains six distributions: a distribution over the (1) μ and (2) σ parameters for the distribution of each participant’s RSA α parameter, a distribution over the (3) μ and (4) σ parameter of the distribution of each participant’s RSA ρ parameter, and a distribution over the (5) α and (6) β parameters for the distribution of each participant’s error parameter Ɛ.
Overall, the generative model is as follows. First, an α, ρ, and Ɛ parameters are drawn for each participant. Then, the RSA production probabilities of each signal are calculated for each stimulus observed by each participant, taking into account the participant’s parameters as well as the stimulus’ properties (number of target objects and total number of objects). Then, the RSA production probabilities are disturbed by adding noise. Finally, each participant samples a quantifier for each stimulus with the noisy production probabilities.
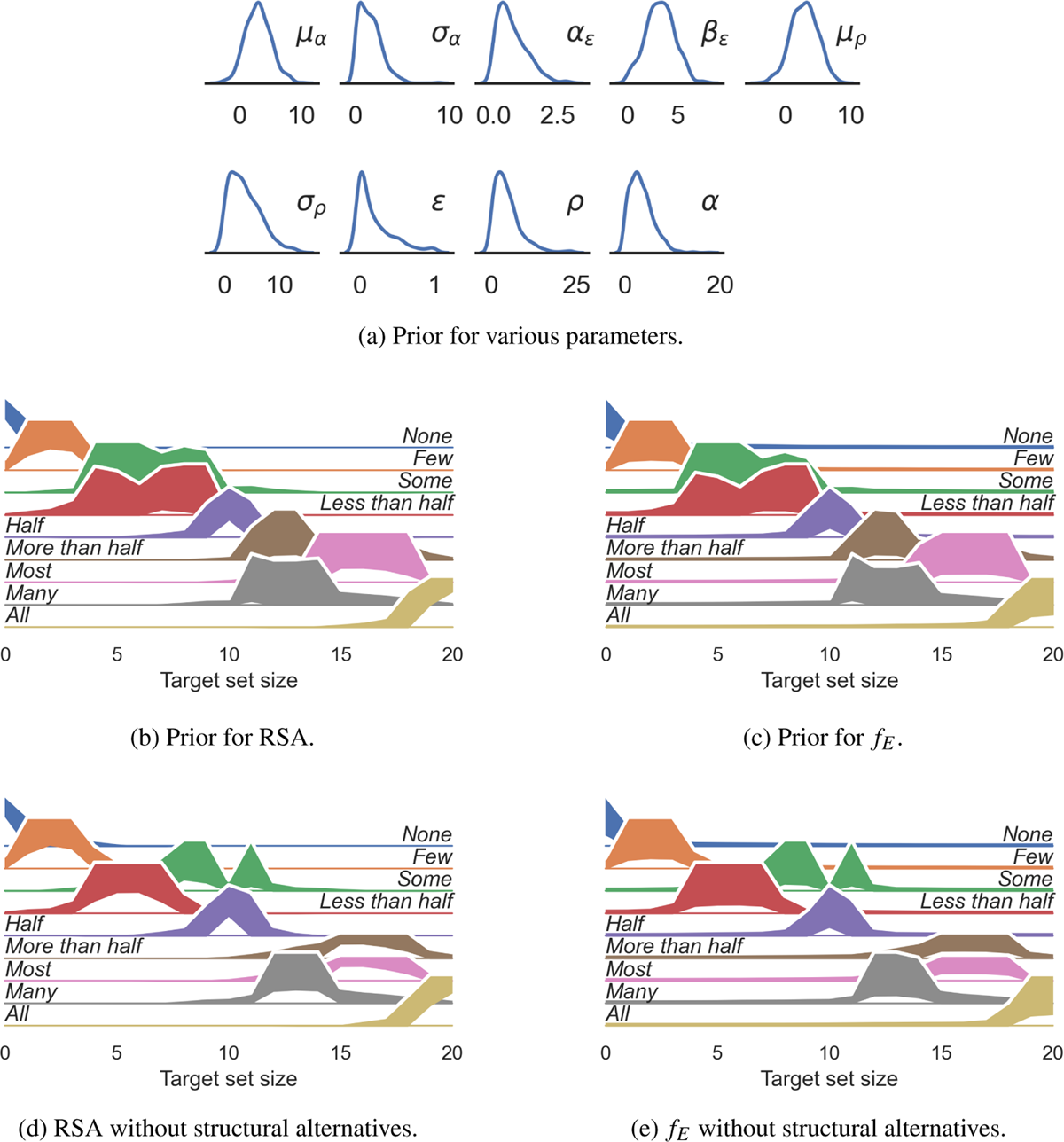
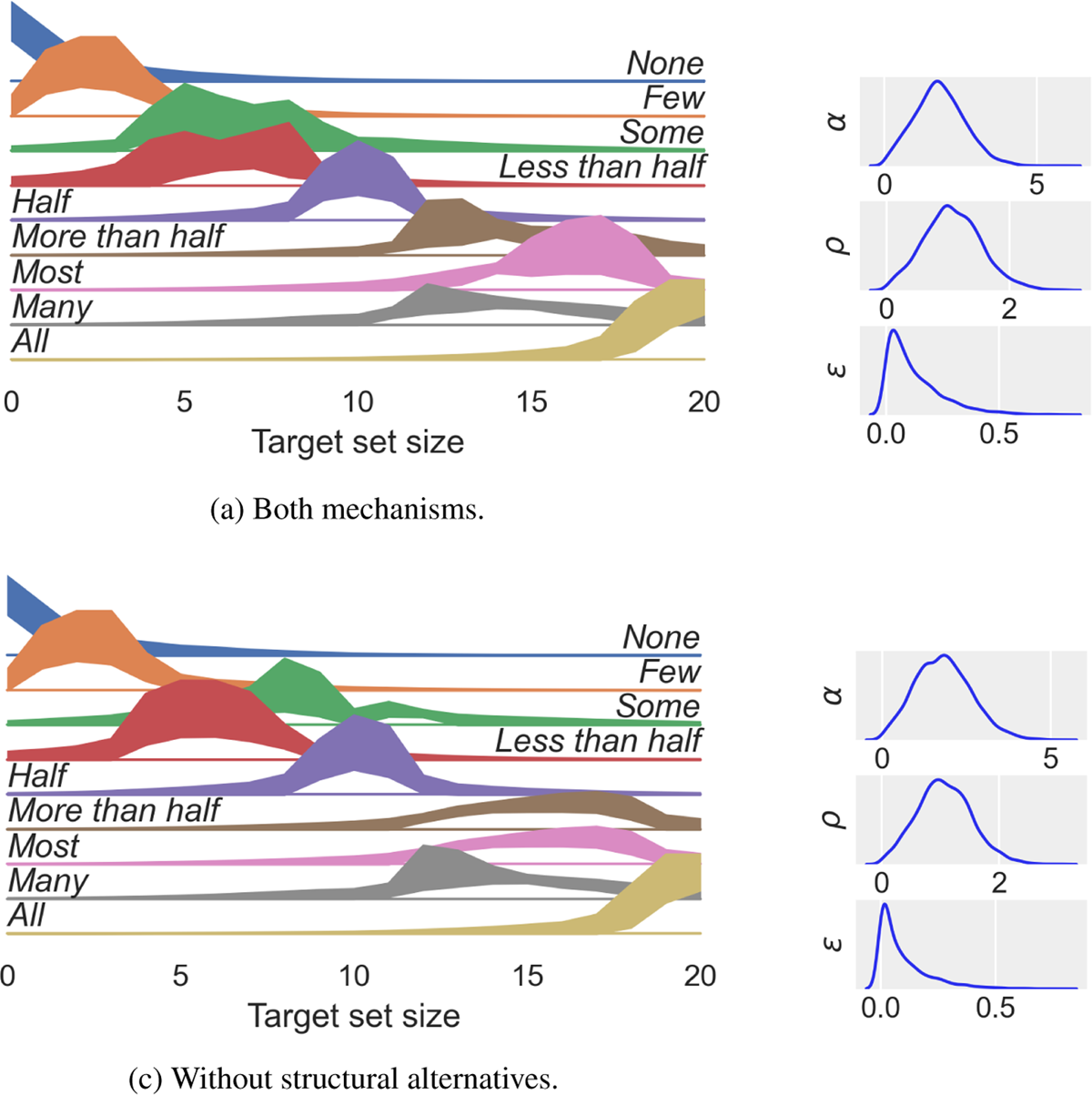
The prior values for the population-level distributions can be seen in Figure 7, and are visualized in Figure 9(a). We chose weakly regularizing priors which included a variety of possible behaviours. The prior predictions at the level of a single participant’s quantifier production behaviour are shown in Figure 8.
Prior predictive simulations. (a) Marginal distribution of prior samples for various model parameters. (b) 95% HPD interval for S2’s behaviour for each signal. (c) 95% HPD interval for predicted participant behaviour, i.e. RSA agent with added noise. The main effect of adding noise is an increased probability of producing signals outside of the usual range of usage of the quantifier. Note that prior predictions of noisy production behaviour includes nearly uniform languages, which appear to be close to 0. because uniform production probabilities are small for each state. Therefore, despite (b) and (c) looking similar, they include substantially different predicted production behaviours. (d) and (e) plot the same information as (b) and (c) respectively, for the model without the structural account of conceptual information. Crucially, in (d) and (e) ‘most’ and ‘more than half’ are used identically.
In addition to the model with the structural account of conceptual alternatives described above, we fit a model without the structural account of conceptual alternatives, where each signal has all and only the other signals seen by the participants as alternatives. The 95% HPD intervals for the marginalized prior production probabilities are shown in Figures 9(d) and 9(e). The model without structural alternatives has the same hyperprior parameters as the model presented above. This model differs from the model with structural alternatives in the predicted production probabilities. First, ‘most’ and ‘more than half’ are used in exactly the same way in the model without structural alternatives. Given the difference in usage between the two expressions that can be seen in the raw data in Figure 5, a lack of predicted difference will diminish the fit to the data. We perform model comparison to quantify the difference in fit between the two models. The second main difference between the two models is in the predicted behaviour of ‘some’. Since ‘more than half’ is now used for higher proportions, and ‘some’ also applies to proportions higher than half, the prediction of the model without structural alternatives is that ‘some’ will be used for proportions slightly higher than half. Since the peak of ‘half’ is very stable across prior samples, even in the marginal distribution ‘some’ has a dip at 0.5.
It is worth noting the way that the noise mechanism affects the estimation for both models. If the noise parameter for a participant is high, the participant’s behaviour will depend less on their α and ρ parameters. Therefore, the participant’s data will give less information about those parameters, influencing less the population-level estimates. On the other hand, since the behaviour and the underlying parameters will be less tied to each other for a noisy participant, the hierarchical model’s estimation of the participant’s RSA parameters will depend more on the population-level distributions. Therefore, the population-level RSA distributions will be impacted less by data of participants estimated to be noisy, and in turn will play a bigger role in estimating the individual-level RSA parameters for such participants. As well as being an intuitive way to deal with noisy participants, this mechanism eliminates the need to define arbitrary criteria for data exclusion.
This section described how we embed the RSA model within a hierarchical Bayesian model whose hidden parameters can be fitted to experimental data. We discussed two models which can be compared, with and without the structural account of alternatives. In the next section, we present the results of fitting for the two models and their comparison.
7.4 Model fitting and results
We fit the models with the Python library PyMC3 (Salvatier et al. 2016), which implements NUTS (No U-Turns Sampler) to fit hierarchical Bayesian models. To reduce computation time without introducing systematic bias in the data, we only fit the model on responses for stimuli where the total number of objects in the picture was greater than or equal to 10. As a result, we have 229 responses for each participant, for a total of 13053 responses. We fit two chains for each of the two model to perform convergence checks. We drew for each chain 3000 NUTS tuning samples and 2000 non-tuning samples. The convergence statistics is close to 1 for all the population-level estimates of both the model with both mechanisms and the model without the structural account of alternatives (‘w/o sa’), indicating that the sampling converged to the posterior.
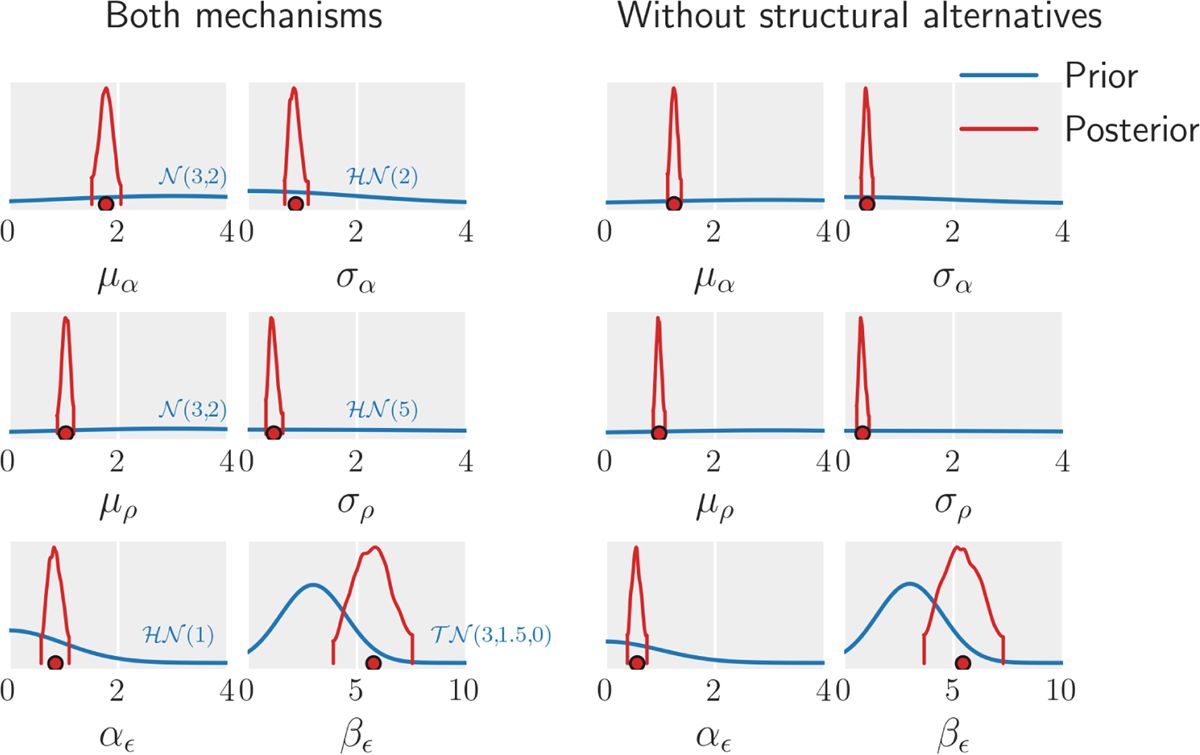
For both of the models, the posterior distributions of all the population-level parameters are substantially more precise than the prior distributions, indicating that the data contained substantial information about the underlying parameters (Figure 9). The plot of the joint distributions does not indicate any strong correlation between population-level distributions.
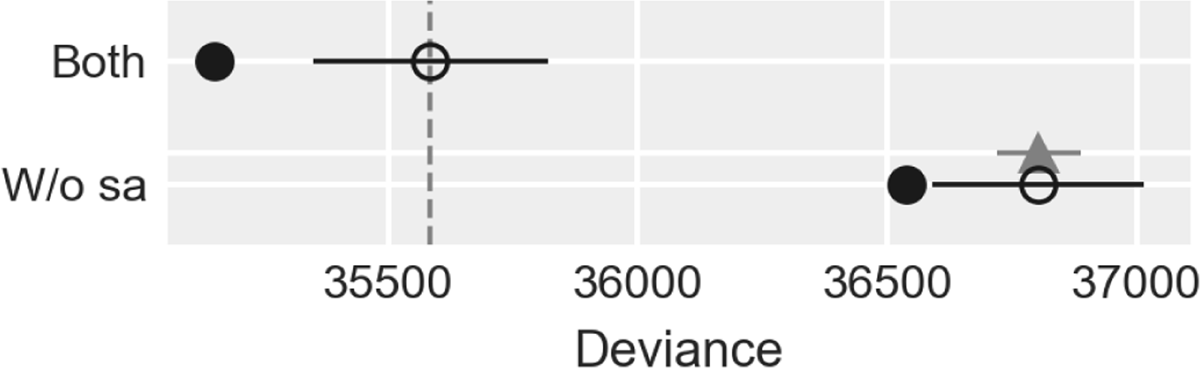
We compare the models with and without the structural account of alternatives with the Watanabe-Akaike Information Criterion (WAIC) (Watanabe 2013; Gelman et al. 2014) (Figure 10), an information criterion that considers the deviance for all posterior samples and is apt for Bayesian analyses. The result of the comparison is that the model with both mechanisms is estimated to have a higher out-of-sample predictive accuracy (WAIC≈ 35584, SE ≈ 235) than the model without the structural account of alternatives (WAIC≈ 36803, SE ≈ 211), with a difference in WAIC of approximately 1218 (SE ≈ 83). This indicates that the structural account of alternatives plays a crucial role in explaining the difference in usage between ‘most’ and ‘more than half’. For both model, the posterior variance of the log predictive density exceeded 0.4 for fewer than 30 of the 13279 observations, and within those was mostly close to 0.4 and never greater than 1.
Comparison of the model with both mechanisms (‘Both’) and the model without structural alternatives (‘W/o sa’) with the WAIC. The plot is on the deviance scale, where smaller values indicate a better fit. The empty circles are the WAIC values for the two models, with their associated standard deviations shown as black bars. The black dots show the in-sample deviance of each model. Finally, the triangle and its error bar show the standard error of the difference between the WAIC of the top ranked model, i.e. the one with both mechanisms, and the WAIC of the model without structural alternatives. The main result in the plot is that the model with both mechanisms performs much better than the model without the structural account of alternatives.
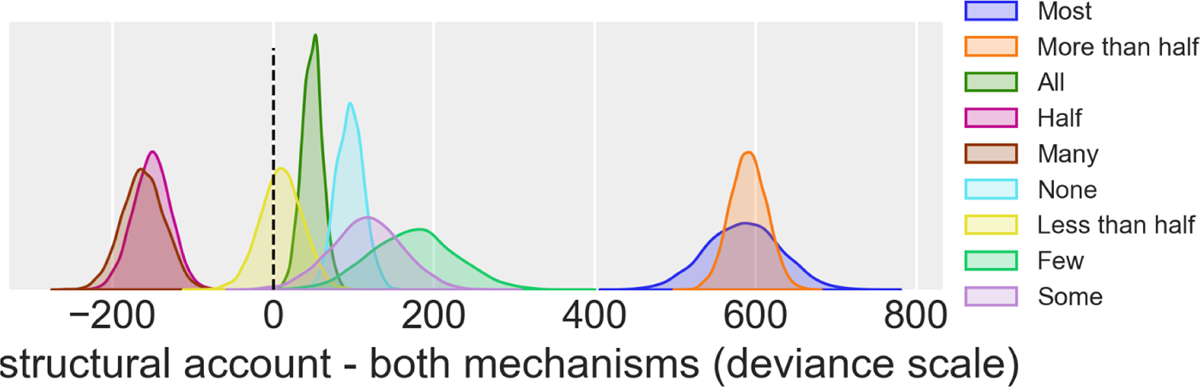
A crucial question about the two models is how well they predict the participants’ behaviour with respect to each of the signals. Figure 11 shows, for each signal, the posterior distribution of the difference between the deviance of the two models across all data points. Predictably, the model including structural alternatives performs much better than the other for ‘most’ and ‘more than half’. However, the in-sample predictive accuracy of the two models differs starkly also for the other signals. This might be a consequence of the model without structural alternatives compromising the fit of the other signals while trying to find parameter values appropriate for ‘most’ and ‘more than half’.
Distribution of differences of posterior signal-wise deviance, marginalized across participants. Positive values indicate better in-sample fit for the model with both mechanisms. The model with the structural account of alternatives performed better for all signals except ‘Many’ and ‘Half’.
Figure 12 shows the posterior predictive simulations. Behaviour for a new participant is predicted by sampling a set of individual-level parameters from the population-level distributions of each posterior sample. For both models, the predictions for a new participant are more precise than the predictions from the prior shown in Figure 12(b). In the case of the model with the structural account of alternatives (Figure 12(a)), the difference is particularly stark for ‘more than half’, ‘most’, and ‘many’. For the model without the structural account of alternatives, the biggest difference from the prior to the posterior is in the distributions of ‘some’ and ‘many’. Moreover, since the marginal distribution of the production error tends more towards 0 in the posterior, adding the production error has a smaller impact on the posterior than the prior.
Posterior predictive simulations (without production error) for a new participant, for 20 total number of objects. We predict a new participant in this plot by sampling a set of individual-level parameters from the population-level distributions defined by each posterior sample and then calculating S2. The left column of plots shows the 95% HPD interval of production probabilities, for the model with both mechanisms and without the structural account of alternatives. Adding production error does not make a substantial visual difference in the plots, as the predicted production error is generally low. The right plots show the distribution of the means of the population-level distributions for the plots on the right.
This section presented two Bayesian hierarchical models encoding two minimally different pictures of how quantifiers are produced, with and without the structural account of alternatives. In sum, model comparison lends strong support to the model which includes the structural account of conceptual alternatives over a minimally different model without it. Moreover, the model with structural alternatives has a closer fit to the data not only for the signals we have discussed—’most’ and ‘more than half’—but also for most of the other signals, a consequence of the fact that in an RSA model the production distributions for the signals are interdependent.
8 Comparison with Solt [2016]
As discussed above, Solt’s account is concerned with a wider variety of phenomena than ours. For what concerns the interpretation of and differences between ‘most’ and ‘more than half’, our and Solt’s accounts have some points of overlap and some important differences. The main point of overlap is that the difference in upper bounds between ‘most’ and ‘more than half’ is explained in both accounts in terms of a difference in the set of alternatives: while ‘more than half’ competes with ‘more two thirds’ and similar utterances, ‘most’ does not. The reason for this difference in the sets of alternatives is different in the two accounts, namely the structural account of alternatives in our model and a difference in the types of scales in Solt’s account. The explanation for the fact that ‘more than half’ has a lower bound closer to 0.5 than ‘most’ is also different in the two models. While in our model it is due to ‘most’ pragmatically competing with an enriched sense of ‘more than half’, in Solt’s account it follows again from a difference in the scales underlying the two expressions, as explained above in Section 2.
In the previous section, we discussed and compared two RSA models with respect to their ability to fit the experimental data, namely a model with and without the structural account of alternatives. It would have been desirable to directly compare the two models with the account proposed in Solt (2016). However, it is unclear how the latter could be implemented in a generative Bayesian cognitive model in something like the production task presented above. The fundamental problem is that Solt (2016)’s account relies on the difference between information on a ratio scale and information on a semi-ordered scale obtained through the approximate number system (henceforth ANS) Dehaene 1999). However, in our experiment almost all the data is approximated via the ANS (except for observations in the subitizing range to which we return below), making it unclear what predictions Solt (2016) would make.
More specifically, in Solt (2016) the signals that the speaker can produce partially depend on the type of available data. In particular, in a literal reading of Solt’s account, ‘more than half’ could not be used for observations on a scale with less structure than a ratio scale. This contradicts the data gathered in our experiment, where the participants use the expressions even for stimuli that we know require the ANS. It is unclear what Solt (2016)’s theory predicts in such cases. An elaboration of Solt’s account could be developed to allow a computational implementation, but it is unclear at the moment how to do so.
This problem was reduced by Solt (2016)’s original corpus data, where the two quantifiers always occurred together with a percentage—Solt’s inclusion criteria for determining the typical sets of the two expressions—effectively weakening the reliance on approximate knowledge. However, the dual problem, namely why ‘most’ is used so often when precise proportions are available, is relevant for Solt (2016)’s data. Occurrences with proportions are precisely those where amounts are known precisely, excluding those scales which, according to Solt, are most typical of ‘most’, namely non-ratio scales. Solt argues that ‘most’ is used even in these cases as if the scale was semi-ordered, since the approximate meaning of ‘most’ becomes an R-implicature. However, this move further detaches the input to the perceptual system and the predicted output, making it harder to extract a production model from Solt’s account.
While the ANS plays a crucial role in Solt (2016)’s account, we did not include it in our model. The reason for this is that the ANS was not necessary for our analysis, i.e., the advantage of having the structural account of alternatives was not conditional on including the ANS, allowing us to keep the model simple. It is prima facie tempting to think that the ANS could play the same role as the distance-minimizing listeners, essentially allowing the speaker to produce a signal for states that are not compatible with its literal meaning but close to it. However, this substitution is not as simple as it might first seem because the ANS can only perform the function of distance-minimization for stimuli outwith the subitizing range.
For stimuli within the subitizing range, e.g., those stimuli where ‘None’ applies, the ANS predicts that participants would only produce signals that literally applied to the stimulus. In contrast to the ANS, the distance-minimizing mechanism applies to every proportion and predicts correctly that participants sometimes use ‘All’ and ‘None’ for non-extreme, albeit close to extreme, proportions. To substitute the distance-minimizing listeners with the ANS, an additional mechanism could be added to the generative model so that participants might miss some of the target stimuli when many non-target stimuli are shown (or vice versa), allowing e.g., for perceptual confusion between 20/20 (target/total) and 19/20. This would allow for misapplication of the literal meaning within the subitizing range while however further complicating the model. In conclusion, while the distance-minimizing listeners do not play as crucial a role as the structural account of alternatives and alternatives could be developed for the former, we leave such developments for future work.
Another difference between our and Solt (2016)’s accounts is the explanation of the difference between ‘more than half’ and ‘less than half’. In Solt’s account, the two are predicted to be symmetric. Solt argues that pragmatic competition between ‘most’ and ‘more than half’ is irrelevant to explain the difference between them: all that is required is that ‘more than half’ is upper bounded by other proportions. Similarly, ‘less than half’ is bounded below by smaller proportions even in the absence of a dual to ‘most’. Therefore, the case of ‘less than half’ is symmetric to the case of ‘more than half’. On the other hand, in our model two factors contribute to the production of ‘most’ and ‘more than half’: first, there is the pragmatic competition with a quantifier’s own set of alternatives for S1 and L1; second, the competition of each quantifier with the other real alternatives at the level of S2. While implicit alternatives like ‘more than 3/4’ might lower the upper bound of ‘more than half’ compared to ‘most’, if ‘most’ was not an available option, ‘more than half’ would be used by S2 for higher proportions for lack of a better signal. Our model, therefore, implies that the two expressions pragmatically compete with each other: ‘more than half’ is upper bounded by the lower bound of ‘most’, and vice versa. Since there is no equivalent of ‘most’ for points below 0.5, a prima facie consequence of our account is that ‘more than half’ and ‘less than half’ should not be symmetric. However, the situation is further complicated by ‘some’ competing with ‘less than half’ at the level of S2 in a way similar to how ‘more than half’ competes with ‘most’. As can be seen in Figure 11, ‘some’ is better explained by the model with structural alternatives, and albeit to a lesser extent, this is also true of ‘less than half’.
Overall, our model offers various advantages over Solt’s account for explaining the proportions for which ‘most’ and ‘more than half’ are used. First, it is a quantitative rather than a verbal model and can be used directly to analyse or predict behaviour as we have done with experimental data above. As discussed, it would not be trivial to expand Solt’s model to make the quantitative predictions that our model makes.
Second, our model offers a unified explanation for bounds of both ‘most’ and ‘more than half’, in contrast to Solt’s disjunctive account. It is, of course, debatable how rich our assumptions are compared to Solt’s. However, it is worth noting that it is easy to overestimate the number of assumptions we make compared to Solt’s because our model makes precise quantitative predictions, which requires accurate assumptions. If Solt’s account were to be made precise enough to generate the kind of quantitative predictions our model generates, further assumptions would need to be introduced, among others: a functional form for the ANS approximation, a decision threshold for considering one point greater than another on semi-ordered scales, a specific set of alternatives for ‘more than half’, a precise mechanism for computing scalar implicatures.
Third, our model is not tailored specifically for the opposition between ‘most’ and ‘more than half’, but can rather fit quantifier production behaviour more generally, as demonstrated above. While no empirical observation is presented which would show that one theory makes the right prediction while the other makes the wrong one, this is partially because Solt’s account makes no clear prediction for most of the data we gathered, since it does not say anything about the way the other quantifiers we analyse interact with ‘most’ and ‘more than half’. Note that this point is different from the fact that our model is quantitative while Solt’s model is qualitative: even if Solt’s model was made specific enough to make quantitative predictions, in its current form it would still only concern ‘most’ and ‘more than half’.
Despite these advantages of our model, we have discussed only one of the features analysed by Solt (2016), namely the proportions for which the quantifiers are used. Solt’s account makes sense of other aspects of the distribution of ‘most’ and ‘more than half’ in the corpus. For instance, Solt finds differences in how the two phrases behave concerning generics, noun phrase structure, kind vs. group nominals, and vagueness. Therefore, Solt’s account explains more of the data concerning ‘most’ and ‘more than half’ than ours. Our account could, in principle, be augmented with some features of Solt’s account. Future research will investigate how much of these other differences can be accounted for by the model presented here.
9 Conclusions
While traditionally assumed to be truth conditionally equivalent, ‘most’ and ‘more than half’ are typically associated with different proportions. In the most developed explanation of this difference, Solt (2016) introduces a difference between the structures of the scales used by the two expressions. In contrast, in this paper we proposed a novel account of the difference based on independently motivated mechanisms. Moreover, we analysed the account’s predictions by implementing it in a popular computational model of pragmatic reasoning, the RSA model. Finally, we presented the results of an experiment based on Pezzelle et al. (2018), and fitted our model to the quantifier production data. We found that our model explained the data better than a minimally similar model without the structural account of alternatives.
The RSA model we presented can be extended in various possible directions. First, a similar model could be used to account for the usage of modified numerals, since a similar contrast to the one discussed here can be found e.g., between ‘more than 100’ and ‘more than 101’, where the typical guessed number for the former utterance is higher than for the latter. More in general, the model presented in this paper applies whenever two synonymous expressions behave pragmatically differently due to their conceptual structure.
Second, in the models we presented we only considered a small set of possible utterances. However, it would be valuable to study the model’s predictions when more alternative utterances are included. One possibility would be to add utterances containing more fine-grained proportions, which would induce a more granular set of alternatives for ‘more than half’. Moreover, Denić & Szymanik (Forthcoming) point out a way in which embedding ‘most’ and ‘more than half’ under negation could adjudicate between the available hypotheses. Specifically, they argue that the lexical meaning hypothesis predicts that the threshold for ‘most’ should remain higher than that for ‘more than half’ under negation. In contrast, the pragmatic strengthening hypotheses predict that the threshold for ‘most’ should be either at 0.5 or lower in negative environments. They run an experiment, finding that the threshold for ‘most’ remains higher than that of ‘more than half’ under negation. The question is then what our RSA model predicts when negation is added. However, results depend on choices on how to implement negation and how many levels of nesting are considered, which go beyond the scope of the present paper. Future work could then explore what the model predictions are when negation is included.
Third, the hierarchical Bayesian model can also be extended in various ways, e.g., by implementing more alternative accounts of the difference between ‘most’ and ‘more than half’ and comparing them to our account. We leave all these exciting possible developments to future work.
In general, the linguistic consequences of adding the structural account of conceptual alternatives to RSA modelling are those that have been identified by Buccola et al. (2021). However, we think that combining the two has advantages for researchers working on RSA modelling and those working on the structural account of conceptual alternatives. First, this combination allows the structural account, which has been a fairly informal theory, to be developed rigorously and to make explicit quantitative assumptions. Second, RSA models need to implement a plausible measure of representational complexity/cost. Whatever this measure is going to be, it will need to be based on some theory of mental complexity of alternatives. The structural account of alternatives delivers this for free along with its other mechanisms, which for instance the Katzirian account does not. While we don’t need to commit to the structural account in its current form necessarily, any theory similar to it will be in principle compatible with our explanation. Of course, here, we can only scratch the surface of the consequences of this view of alternatives. Further work is needed to determine how successful the combination of RSA and the conceptual account of alternatives is.
Data availability/Supplementary files
The anonymized data, as well as the code for model fitting in PyMC3 and for analyzing the traces can be found in the following GitHub repository: https://github.com/thelogicalgrammar/mostVsMoreThanHalf.
Ethics and Consent
The study was approved by the European Research Council and the University of Amsterdam, Faculty of Humanities Ethics Committee. Informed consent was obtained for each participant prior to the experiment.
Notes
- In what follows, we assume that ‘A’ and ‘B’ refer to two finite sets A and B. We give Solt (2016)’s more general definition in terms of measure functions below. [^]
- This type of semi-ordered structure has been proposed as a cognitive model of perception of quantities (Gescheider 2013), preferences (Luce 1956), and numbers (Dehaene 1999). [^]
- There are features for which two individuals might be more or less close to each other, but this does not concern their identity as such. [^]
- This communicative setup is called descriptive by Franke (2014), who opposes it to referential communicative games. In what follows, we limit ourselves to discussions of descriptive communication. [^]
- In what follows, we will focus on the scale of proportions, but what we say can be easily generalized to the scale of integers. [^]
- Katzirian alternatives can also be used if ‘more than one half’ is considered instead of ‘more than half’. [^]
- For a discussion of the role of granularity in scalar language, see e.g., Cummins et al. (2012). [^]
- The lexicalization of the fractional concept 1/2 with the omission of ‘one’ in ‘one half’ has a pragmatic justification: ‘one’ (or ‘a’) is generally superfluous when combined with ‘half’, since except in very rare occasions ‘two halves’ would not be uttered, given the simpler available option ‘one’. This is opposed to every other denominator, which can informatively combine with more than one numerator in a way that is not reducible to other fractions. [^]
- Cf previous work where the effects of a distance structure affect the speaker but not the listener, such as Franke (2014). It is worth noticing that our model does not have more degrees of freedom than Franke’s model. While we introduce one more parameter than the basic RSA model to regulate the listener’s tendency to minimize expected distance, Franke introduces one parameter to regulate the amount of pragmatic slack. We do not investigate in this work the differences between the two approaches. [^]
- We apply this modification only to L1, assuming that the attempt to minimize distance is something above and beyond the literal reading of the signals. We leave to future work an investigation of the effects of modifying both listeners. [^]
- It would be interesting to explore the consequences of lifting this assumptions. We leave this to future work. [^]
- Previous work has argued that utterances with different monotonicity profiles do not appear in the same set of alternatives (e.g. Horn 1989). This observation would be contradicted by the set of sets of alternatives we consider. However, Katzir (2007) has argued that the structural theory of alternatives makes this restriction superfluous. [^]
- https://www.prolific.co/. [^]
Acknowledgements
We would like to thank Sonia Ramotowska and Simone Astarita for help with collecting the data, and Milica Denić, Sandro Pezzelle, and the audiences of Meaning, Language, and Cognition seminar in Amsterdam and the Society for Computation in Linguistics for discussions. Moreover, we would like the thank anonymous reviewers for their valuable feedback.
Funding Information
The authors have received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/20072013)/ERC Grant Agreement n. STG 716230 CoSaQ.
Competing Interests
The authors have no competing interests to declare.
References
Ariel, Mira. 2003. Does most mean ‘more than half’? Annual Meeting of the Berkeley Linguistics Society 29(1). 17–30. DOI: http://doi.org/10.3765/bls.v29i1.982
Barwise, Jon & Cooper, Robin. 1981. Generalized quantifiers and natural language. Linguistics and Philosophy 4(2). 159–219. DOI: http://doi.org/10.1007/BF00350139
Bastiaanse, Harald. 2011. The Rationality of Round Interpretation. In Nouwen, Rick & van Rooij, Robert & Sauerland, Uli & Schmitz, Hans-Christian (eds.), Vagueness in Communication (Lecture Notes in Computer Science), 37–50. Berlin, Heidelberg: Springer. DOI: http://doi.org/10.1007/978-3-642-18446-8_3
Breheny, Richard & Klinedinst, Nathan & Romoli, Jacopo & Sudo, Yasutada. 2018. The symmetry problem: Current theories and prospects. Natural Language Semantics 26(2). 85–110. DOI: http://doi.org/10.1007/s11050-017-9141-z
Buccola, Brian & Križ, Manuel & Chemla, Emmanuel. 2021. Conceptual alternatives: Competition in language and beyond. Linguistics and Philosophy. DOI: http://doi.org/10.1007/s10988-021-09327-w
Carcassi, Fausto. 2020. The Cultural Evolution of Scalar Categorization. Edinburgh: University of Edinburgh PhD Thesis.
Carcassi, Fausto & Sbardolini, Giorgio. 2021. Updates and Boolean Universals. Unpublished.
Carcassi, Fausto & Schouwstra, Marieke & Kirby, Simon. 2020. The Advantage of Extreme Meanings in Cultural Evolution. In Ravignani, Andrea & Barbieri, Chiara & Martins, Mauricio & Flaherty, Molly & Jadoul, Yannick & Lattenkamp, Ella & Little, Hannah & Mudd, Katie & Verhoef, Tessa (eds.), The Evolution of Language: Proceedings of the 13th International Conference (EvoLang13), 24–26. https://doi.org/10/ggm28x
Carcassi, Fausto & Szymanik, Jakub. Forthcoming. The Shape of Modified Numerals. Proceedings of the 43rd Annual Meeting of the Cognitive Science Society.
Chemla, Emmanuel. 2007. French both: A gap in the theory of antipresupposition. Snippets 15. 4–5.
Cummins, Chris & Sauerland, Uli & Solt, Stephanie. 2012. Granularity and scalar implicature in numerical expressions. Linguistics and Philosophy 35(2). 135–169. DOI: http://doi.org/10.1007/s10988-012-9114-0
Davies, Mark. 2017. Corpus of Contemporary American English (COCA). DOI: http://doi.org/10.7910/DVN/AMUDUW
Dehaene, Stanislas. 1999. The Number Sense: How the Mind Creates Mathematics. New York: Oxford University Press.
Denić, Milica & Szymanik, Jakub. Forthcoming. Differences in thresholds between ‘most’ and ‘more than half’: Semantics or pragmatics? In Sinn und Bedeutung 25. London: OSF.
Fox, Danny & Katzir, Roni. 2011. On the characterization of alternatives. Natural Language Semantics 19(1). 87–107. DOI: http://doi.org/10.1007/s11050-010-9065-3
Frank, Michael. 2017. Rational speech act models of pragmatic reasoning in reference games. PsyArXiv. DOI: http://doi.org/10.31234/osf.io/f9y6b
Franke, Michael. 2014. Typical use of quantifiers: A probabilistic speaker model. Proceedings of the 36th Annual Conference of the Cognitive Science Society 36. 487–492.
Gardenfors, Peter. 2004. Conceptual Spaces: The Geometry of Thought. Cambridge, Mass.: Bradford Books revised edition edn.
Gelman, Andrew & Hwang, Jessica & Vehtari, Aki. 2014. Understanding predictive information criteria for Bayesian models. Statistics and Computing 24(6). 997–1016. DOI: http://doi.org/10.1007/s11222-013-9416-2
Gescheider, George A. 2013. Psychophysics: The Fundamentals. Psychology Press. DOI: http://doi.org/10.4324/9780203774458
Goodman, Noah & Stuhlmüller, Andreas. 2013. Knowledge and Implicature: Modeling Language Understanding as Social Cognition. Topics in Cognitive Science 5(1). 173–184. DOI: http://doi.org/10.1111/tops.12007
Hackl, Martin. 2000. Comparative determiners. Cambridge, Mass.: MIT dissertation.
Hackl, Martin. 2009. On the grammar and processing of proportional quantifiers: Most versus more than half. Natural Language Semantics 17(1). 63–98. DOI: http://doi.org/10.1007/s11050-008-9039-x
Horn, Laurence. 1989. A natural history of negation. Chicago: University of Chicago Press.
Jäger, Gerhard & Metzger, Lars & Riedel, Frank. 2011. Voronoi languages: Equilibria in cheaptalk games with high-dimensional types and few signals. Games and Economic Behavior 73(2). 517–537. DOI: http://doi.org/10.1016/j.geb.2011.03.008
Katzir, Roni. 2007. Structurally-defined alternatives. Linguistics and Philosophy 30(6). 669–690. DOI: http://doi.org/10.1007/s10988-008-9029-y
Luce, Duncan. 1956. Semiorders and a Theory of Utility Discrimination. Econometrica 24(2). 178–191. DOI: http://doi.org/10.2307/1905751
Peirce, Jonathan & Gray, Jeremy & Simpson, Sol & MacAskill, Michael & Höchenberger, Richard & Sogo, Hiroyuki & Kastman, Erik & Lindeløv, Jonas Kristoffer. 2019. PsychoPy2: Experiments in behavior made easy. Behavior Research Methods 51(1). 195–203. DOI: http://doi.org/10.3758/s13428-018-01193-y
Peters, Stanley & Westerståhl, Dag. 2006. Quantifiers in Language and Logic. Oxford University Press UK.
Pezzelle, Sandro & Bernardi, Raffaella & Piazza, Manuela. 2018. Probing the mental representation of quantifiers. Cognition 181. 117–126. DOI: http://doi.org/10.1016/j.cognition.2018.08.009
Ramotowska, Sonia & Steinert-Threlkeld, Shane & van Maanen, Leendert & Szymanik, Jakub. 2019. Most, but not more than half, is proportion-dependent and sensitive to individual differences. In Franke, Michael & Kompa, Nikola & Liu, Mingya & Mueller, Jutta L. (eds.), Proceedings of Sinn und Bedeutung 24, 165–182. Osnabrueck: Schwab.
Rett, Jessica. 2018. The semantics of many, much, few, and little. Language and Linguistics Compass 12(1). 1–18. DOI: http://doi.org/10.1111/lnc3.12269
Romero, Maribel. 2015. The conservativity of many. In Brochhagen, T. & Roelofsen, F. & Theiler, N. (eds.), Proceedings of the 20th Amsterdam Colloquium, 20–29. Amsterdam.
Salvatier, John & Wiecki, Thomas & Fonnesbeck, Christopher. 2016. Probabilistic programming in Python using PyMC3. PeerJ Computer Science 2. e55. DOI: http://doi.org/10.7717/peerj-cs.55
Sarnecka, Barbara & Lee, Michael. 2009. Levels of Number Knowledge in Early Childhood. Journal of experimental child psychology 103(3). 325–337. DOI: http://doi.org/10.1016/j.jecp.2009.02.007
Scontras, Gregory & Tessler, Michael Henry & Franke, Michael. 2021. Probabilistic Language Understanding: An introduction to the Rational Speech Act framework. https://www.problang.org/.
Solt, Stephanie. 2016. On measurement and quantification: The case of most and more than half. Language 92(1). 65–100. DOI: http://doi.org/10.1353/lan.2016.0016
Spector, Benjamin. 2007. Aspects of the Pragmatics of Plural Morphology: On Higher-Order Implicatures. In Sauerland, Uli & Stateva, Penka (eds.), Presupposition and Implicature in Compositional Semantics, 243–281. London: Palgrave Macmillan UK. DOI: http://doi.org/10.1057/9780230210752_9
Stevens, Stanley Smith. 1946. On the Theory of Scales of Measurement. Science, New Series 103(2684). 677–680. DOI: http://doi.org/10.1126/science.103.2684.677
Szymanik, Jakub. 2016. Quantifiers and Cognition: Logical and Computational Perspectives (Studies in Linguistics and Philosophy). Springer International Publishing. DOI: http://doi.org/10.1007/978-3-319-28749-2
Trinh, Tue & Haida, Andreas. 2015. Constraining the derivation of alternatives. Natural Language Semantics 23(4). 249–270. DOI: http://doi.org/10.1007/s11050-015-9115-y
van Benthem, Johan. 1986. Essays in Logical Semantics (Studies in Linguistics and Philosophy). Springer Netherlands. DOI: http://doi.org/10.1007/978-94-009-4540-1
van Benthem, Johan. 1987. Towards a Computational Semantics. In Gärdenfors, Peter (ed.), Generalized Quantifiers, 31–71. Reidel Publishing Company. DOI: http://doi.org/10.1007/978-94-009-3381-1_2
Watanabe, Sumio. 2013. A Widely Applicable Bayesian Information Criterion. Journal of Machine Learning Research 14. 867–897.