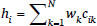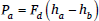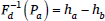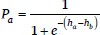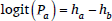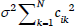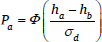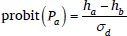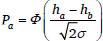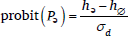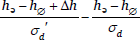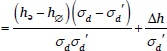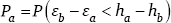1. Introduction
Stochastic phonological grammars assign probabilities to outputs, making it possible to analyze variation and gradient acceptability in phonology. While phonological variation has long been a central concern in sociolinguistics (e.g. Labov 1969), it has only received sustained attention in phonological theory in the last twenty years. The goal of this paper is to compare and empirically evaluate two proposals concerning the proper framework for formulating stochastic grammar: Maximum Entropy (MaxEnt) grammar (Goldwater & Johnson 2003; Hayes & Wilson 2008), and Noisy Harmonic Grammar (NHG) (Boersma & Pater 2016).
MaxEnt grammar is currently the most widely used framework for stochastic phonological grammars. It is based on Harmonic Grammar (Smolensky & Legendre 2006), which is similar to Optimality Theory (Prince & Smolensky 2004), but uses numerical constraint weights in place of constraint rankings. There is a range of evidence that MaxEnt grammar is empirically superior to a probabilistic version of standard Optimality Theory, Stochastic OT (e.g. Zuraw & Hayes 2017; Hayes 2020; Smith & Pater 2020), but there is much less evidence concerning the relative merits of the different varieties of stochastic Harmonic Grammar, MaxEnt and NHG.
Maxent grammar and NHG at least superficially involve very different approaches to making Harmonic Grammar stochastic: MaxEnt takes the harmony scores assigned by a Harmonic Grammar and maps them onto probabilities, while NHG derives variation by adding random ‘noise’ to constraint weights. Given this difference we would expect these frameworks to be empirically distinguishable, but while previous work has demonstrated distinct predictions of the two frameworks (Jesney 2007; Hayes 2017), these have not led to clear empirical tests.
The approach adopted here is to identify a uniform framework for analyzing and comparing stochastic Harmonic Grammars. We then use analysis based on this uniform framework to draw out distinct predictions of MaxEnt and NHG, and test these predictions against data on variable realization of schwa in French (Smith & Pater 2020).
In the uniform framework for stochastic Harmonic Grammars proposed here, Harmonic Grammar is made stochastic by adding random noise to the harmony scores of candidates, then selecting the candidate with the highest harmony. We will see that the difference between MaxEnt and NHG lies in the distribution of the noise: independent Gumbel noise in MaxEnt grammar, and normal noise that can be correlated between candidates in NHG. Variants of these grammar formalisms can easily be accommodated in the same framework, such as a variant of MaxEnt grammar with independent normal noise.
Given this formulation of stochastic Harmonic Grammars, the probability of a candidate being selected is the probability that its harmony is higher than that of any other candidate. This probability depends on the distribution of the noise added to candidate harmonies, so the relationship between harmony and candidate probabilities differs between stochastic Harmonic Grammar frameworks. Specifically, it will be shown that in MaxEnt the relative probabilities of two candidates depends only on the difference in their harmonies, whereas in NHG it also depends on the pattern of their constraint violations. This difference leads to testable predictions concerning the effects on the probabilities of candidates of adding or subtracting constraint violations from a tableau. We will see that testing these predictions against data from Smith & Pater’s (2020) study of variable realization of schwa in French ultimately supports the predictions of MaxEnt over NHG, but development of the methods for comparing these models are as important as a comparison with respect to a single data set.
In the next section we review Harmonic Grammar, and the two dominant proposals for making Harmonic Grammar stochastic, MaxEnt and NHG.
2. Harmonic Grammar
Harmonic Grammar (Smolensky & Legendre 2006) has the same basic structure as Optimality Theory: the output for a given input is the form that best satisfies a set of constraints, but whereas in Optimality Theory conflicts between constraints are resolved by reference to a ranking of the constraints, with the higher-ranked constraint prevailing, in Harmonic Grammar constraints have numerical weights.
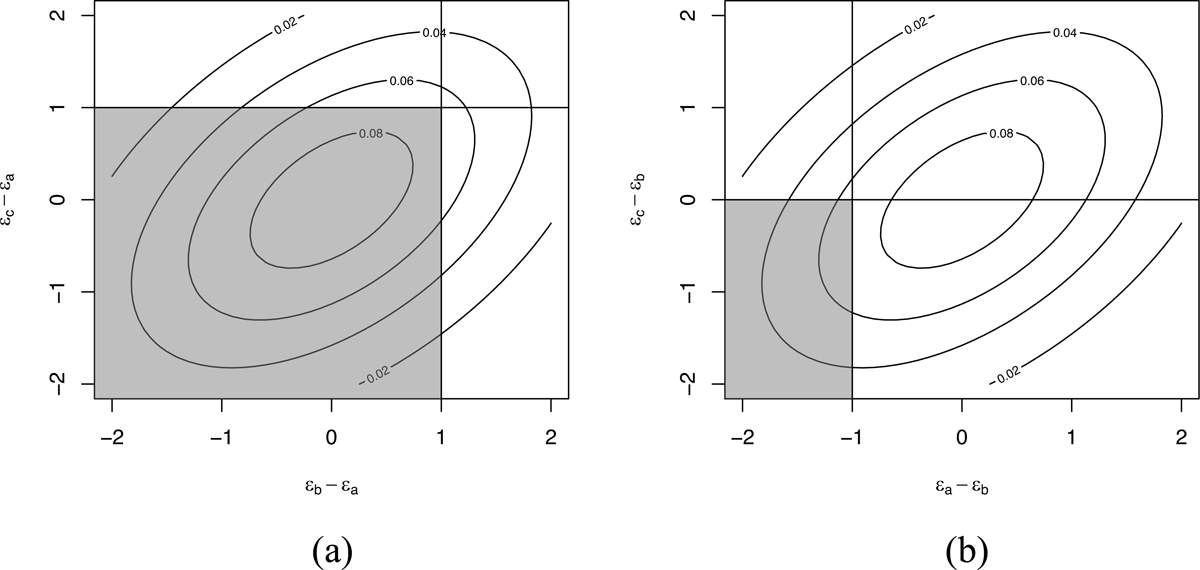
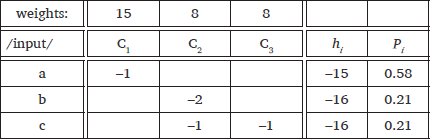
The mechanics of Harmonic Grammar are illustrated by the tableau in (1). The constraint weights are shown in the top row of the tableau. Constraints assign violations, as in OT, but the violations are negative integers, representing the number of times that the relevant candidate violates the constraint. Candidates are compared in terms of the sum of their weighted constraint violations, or harmony score. The harmony score of a candidate i, hi, is calculated according to the formula in (2), where N is the number of constraints, wk is the weight of constraint k, and cik is the violation score assigned to candidate i by constraint k. That is, each constraint violation is multiplied by the weight of that constraint, and the results are summed to yield the harmony score of that candidate. These harmony scores are recorded in the last column of (1). For example, candidate (c) violates constraints C2 and C3 once each. Each constraint has a weight of 8, so the harmony of candidate (c) is (8 × –1) + (8 × –1) = –16. The winning candidate is the one with the highest harmony, which is candidate a in (1).
- (1)
- Harmonic Grammar tableau
- (2)
As can be seen from this example, Harmonic Grammar is deterministic, like standard Optimality Theory. That is, each input is mapped onto a single output, the optimal candidate for that input, so Harmonic Grammar must be modified to be able to assign probabilities to candidates. We turn now to the two main proposals for making Harmonic Grammar probabilistic.
3. Stochastic Harmonic Grammars
As observed in the introduction, the two main approaches to making Harmonic Grammar probabilistic are Noisy Harmonic Grammar and Maximum Entropy Grammar.
3.1 Noisy Harmonic Grammar
In Noisy Harmonic Grammar (NHG), Harmonic Grammar is made stochastic by adding random ‘noise’ to each constraint weight at each evaluation. As a result, even with a fixed input, the harmony of a given candidate varies each time we derive an output, so different candidates can win on different occasions.
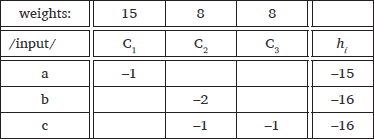
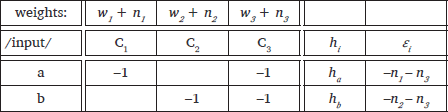
In Boersma & Pater (2016), the noise that is added to each constraint weight, nk, is drawn from a normal distribution with mean of 0 and standard deviation of 1. The result is that constraint weights are random variables rather than fixed quantities, as indicated in (3), the NHG version of the tableau from (1). So, for example, the weight on constraint C1 is 15 + n1, where n1 receives a different value on each evaluation. Since the harmony of a candidate is the weighted sum of its constraint violations, it is affected by the noise added to the weights of each of the constraints that it violates. For example, the harmony of candidate (c) is ((8 + n2) × –1) + ((8 + n3) × –1) = –16 – n1 – n2. In the tableau in (3), the harmonies of each candidate are split into their fixed component, hi, and their random component, which is recorded in the column labelled εi.
The probability of a candidate being selected as the output is the probability that it has higher harmony than all the other candidates. These probabilities are recorded in the last column of (3), headed Pi. We will discuss how to calculate these probabilities below.
- (3)
- Noisy Harmonic Grammar tableau
3.2 Maximum Entropy Grammar
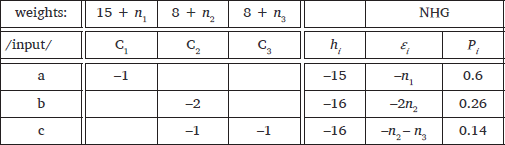
Maximum Entropy Grammar is also a stochastic form of Harmonic Grammar, but adopts what appears to be a very different mechanism from Noisy Harmonic Grammar, directly mapping candidate harmonies onto probabilities (Goldwater & Johnson 2003; Hayes & Wilson 2008). Specifically, the probability of a candidate is given by the formula in (4), where Pi is the probability of candidate i, hi is the harmony of candidate i, and j ranges over the set of candidates. For example, the probability of candidate (a) in (5), Pa, is e–15 divided by e–15 + e–16 + e–16, which is 0.58.
- (4)
- Probability of candidate i in MaxEnt Grammar:

The formula in (4) can be understood as asserting that the probability of a candidate is proportional to the exponential of its harmony, ehi. To ensure that the probabilities of the candidates jointly sum to 1, the exponentiated harmony of each candidate must be divided by the sum of the exponentiated harmonies of all of the candidates.
- (5)
- Maximum Entropy Grammar tableau
Comparing the tableaux in (4) and (5) it can be seen that NHG and MaxEnt can yield different probabilities when applied to the same HG tableau. Of course, both assign the highest probability to the candidate with the highest harmony, candidate (a), but MaxEnt assigns equal probability to candidates (b) and (c) because they have equal harmony, while tableau (3) shows that relationship between harmony and probability is less straightforward in NHG, because it assigns a higher probability to candidate (b) than to candidate (c).
This comparison shows that these two proposals for stochastic versions of Harmonic Grammar make different predictions. The goal of the paper is to draw out these differences so they can be tested against data. The strategy we adopt in comparing and contrasting these models is to reformulate them in a common framework. This helps to clarify their similarities and differences, and situates then within a broader space of Stochastic Harmonic Grammar models. The common framework we use to characterize these models is that of Random Utility Models, a type of model that is widely used to model choice between discrete alternatives in economics (e.g. Train 2009). In the next section, we show that, in spite of their superficial differences NHG and MaxEnt grammar can both be formulated as Random Utility Models.
4. NHG and MaxEnt as Random Utility Models
The common format we will use to analyze and compare stochastic Harmonic Grammars in one in which the harmony of candidate i is composed of hi + εi, where εi is a random variable, or ‘noise’. The addition of noise to candidate harmonies makes the grammar probabilistic because the identity of the candidate with the highest harmony depends on the values of the random variables, εi. This type of model is referred to as a Random Utility Model in economics (e.g. Train 2009).
It is straightforward to map NHG onto this structure: Although we described the random noise as being added to the constraint weights rather than to the harmonies of each candidate, the resulting harmony expression can be separated into fixed and random parts, hi and εi, where εi is a function of the noise variables, nk, that are added to the constraint weights. This decomposition is illustrated in (3). These noise terms, εi, are sums of normal random variables, and sums and differences of normal random variables are also normally distributed. As will be discussed in detail below, the variance of the εi depends on the number of nk variables that are summed together to make up that εi.
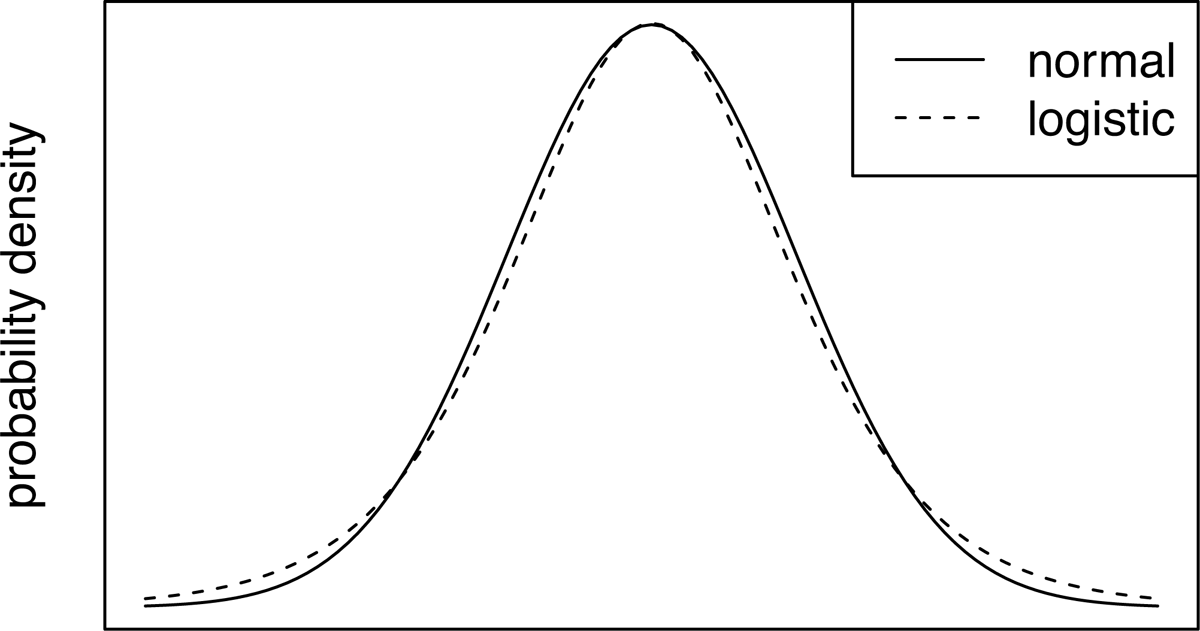
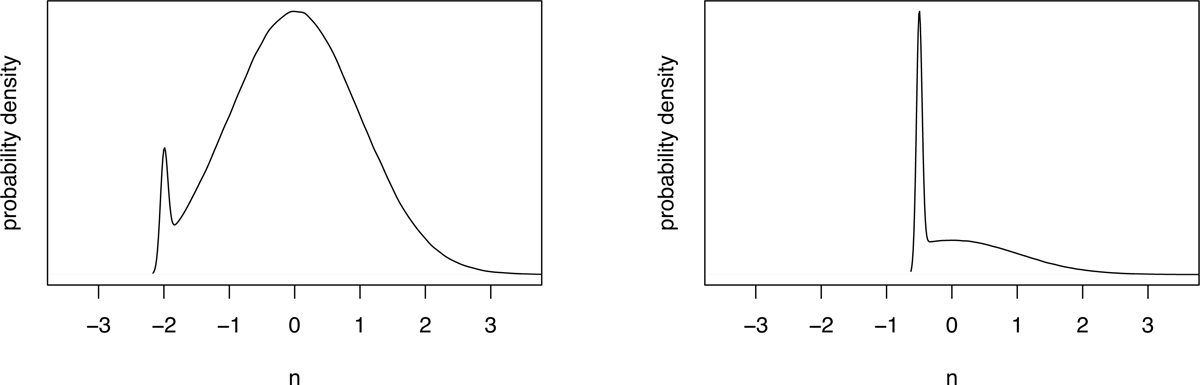
It is less obvious that MaxEnt Grammar can be reformulated as a Random Utility Model, but it is a basic result in the analysis of these models that the MaxEnt equation (4) follows from a Random Utility Model where the εi noise terms are independent and all drawn from the same Gumbel distribution (Train 2009: 74f.). The Gumbel distribution, also known as the Extreme Value Type I distribution, is shown in Figure 1.
Thus NHG and MaxEnt can be analyzed as adopting the same basic strategy for making Harmonic Grammar stochastic: add random noise to the harmony of each candidate. The difference between the models lies in the nature of the noise that is added to candidate harmonies: In MaxEnt the noise terms are drawn from identical Gumbel distributions, whereas in NHG, the noise terms are drawn from normal distributions whose variance depends on the number of constraint violations.
This analysis suggests a space of possibilities for stochastic Harmonic Grammars differentiated by the nature of the noise that is added to candidates’ harmonies. An obvious third candidate to consider is one which is like MaxEnt in that the noise terms are independent and drawn from identical distributions, but the distribution is the more familiar normal distribution, in place of the Gumbel distribution (Figure 1). We will see that this model is similar to MaxEnt, but exhibits some significant differences. In addition, it is commonly proposed that NHG should include a restriction against noise making a constraint weight negative (e.g. Boersma & Pater 2016), so noise is drawn from sums of censored normal distributions, as discussed in Section 7.3, so we will consider this variant also.
The Random Utility Model formulation of stochastic Harmonic Grammars provides the basis for a general analysis of the relationship between harmony and candidate probabilities in these frameworks. We will see that the testable differences between stochastic Harmonic Grammar frameworks follow from differences in this relationship. Specifically, in MaxEnt the relative probabilities of two candidates depends only on the difference in their harmonies, whereas in NHG the relative probabilities of candidates also depend on the pattern of their constraint violations. We turn to this analysis next.
5. The relationship between harmony and probability in Stochastic HGs
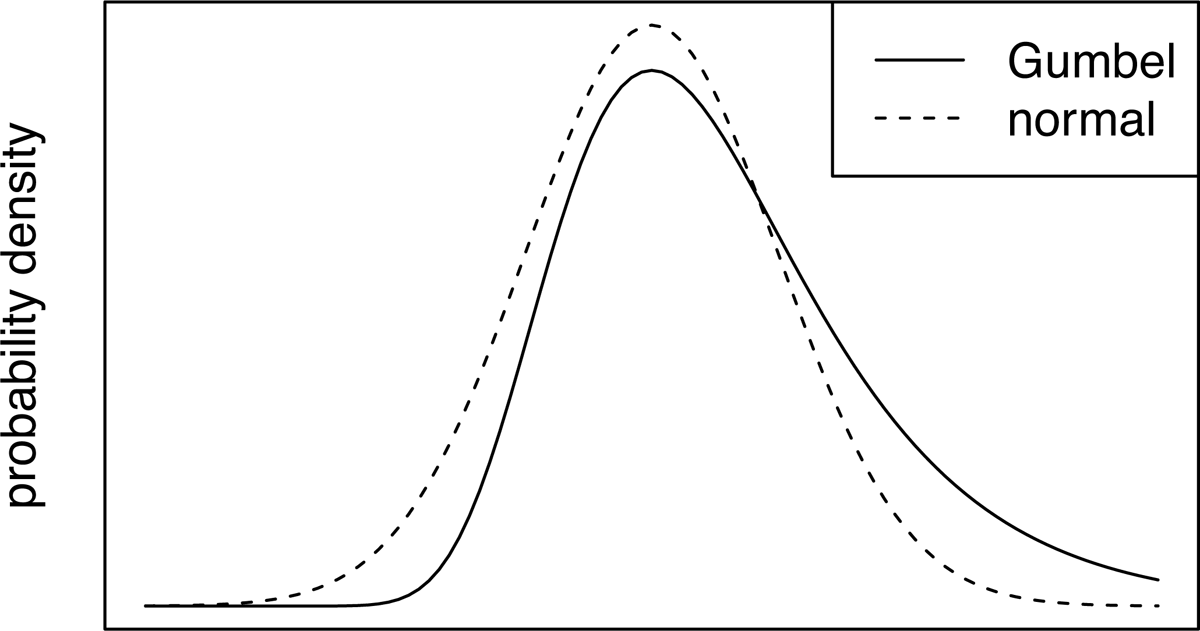
The building block for a general analysis of the relationship between the harmonies and probabilities of candidates is an analysis of the competition between two candidates. Given two candidates, a and b, with harmonies ha + εa and hb + εb, respectively, the probability of candidate a winning, Pa, is the probability that ha + εa > hb + εb. This is the same as the probability that εb – εa < ha – hb, so the probability of candidate a winning is given by the expression in (6).
- (6)
This situation is illustrated in Figure 2. We will refer to the difference in candidate noise terms, εb – εa, as d, a random variable with some probability density, plotted for illustrative purposes as a normal distribution in the figure. The probability of candidate a being chosen, Pa, is the probability that d falls below the difference in candidate harmonies, ha – hb. This probability corresponds to the area under the density function of d that falls below that threshold, i.e. the shaded region in the figure.
The probability of a random variable having a value below some threshold is given by the cumulative distribution function of that variable, so Pa is given by (7), where Fd is the cumulative distribution function of d. From (7) we can see that the probability of candidate a being preferred over candidate b depends on the difference in their harmonies and on the distribution of the noise difference d. The absolute values of candidate harmonies are irrelevant, and it is the distribution of differences between noise terms, d, that is relevant, not the individual distributions of εa and εb.
- (7)
We will see that it is also useful to be able to express the harmony difference between candidates as a function of candidate probabilities. This is achieved by applying the inverse of Fd to both sides of (7), deriving (8).
- (8)
5.1 Harmony and probability in MaxEnt
The differences between varieties of stochastic HG lie in the nature of the cumulative distribution function, Fd. In MaxEnt, the εi are drawn from identical Gumbel distributions. The difference between two standard Gumbel random variables follows a standard logistic distribution, so d follows this distribution. The logistic distribution is symmetrical and bell-shaped, very similar to the normal distribution, but with slightly fatter tails (Figure 3).
The logistic cumulative distribution function Fd(x) = 1/(1 + e–x), so the probability of candidate a in MaxEnt is given by (9). The inverse cumulative distribution function, 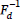 , is the logit function, log(x/(1 – x)), so logit(Pa) is equal to the difference in candidate harmonies (10). Logit(Pa) is log(Pa/(1 – Pa)), but where there are only two candidates, a and b, 1 – Pa = Pb, so logit(Pa) equals log(Pa/Pb). Thus in MaxEnt there is a simple and direct relationship between the harmonies of candidates and their relative probabilities.
, is the logit function, log(x/(1 – x)), so logit(Pa) is equal to the difference in candidate harmonies (10). Logit(Pa) is log(Pa/(1 – Pa)), but where there are only two candidates, a and b, 1 – Pa = Pb, so logit(Pa) equals log(Pa/Pb). Thus in MaxEnt there is a simple and direct relationship between the harmonies of candidates and their relative probabilities.
- (9)
- (10)
Note that expression in (9) looks different from the formula we derive by applying the usual MaxEnt probability formula in (4) to the case of two candidates (11), but the two are in fact equivalent: (11) is derived from (9) by multiplying its numerator and denominator by eha.
- (11)
5.2 Harmony and probability in NHG
The relationship between harmony and probability is more complicated in NHG. As discussed above, in NHG noise is added to constraint weights, so the εi are sums of these noise terms, nk (cf. 12). The nk are independent normal random variables, each with variance σ2. Sums and differences of normal random variables are also normal random variables, so the εi and the noise difference d = εb – εa are all normal.
- (12)
- Noisy Harmonic Grammar tableau
The variance of the εi depends on the number of noise variables, nk, that are summed together and that depends in turn on the number of constraint violations incurred by that candidate, because each constraint violation introduces another nk component, as can be seen in (12). The noise term for a given constraint, nk, is multiplied by the number of violations of that constraint, cik. If an individual noise term, nk, has variance σ2, then multiplying it by the number of violations cik increases its variance to cik2σ2 because multiplying a normal random variable by a constant increases its standard deviation by the same multiplicative factor, and thus increases its variance by the square of the multiplicative factor. This generalizes to the case where a candidate does not violate constraint k, because in that case cik = 0, so the variance of the noise term is 0, i.e. the noise term is canceled out. So the noise added to candidate i by constraint k has variance cik2σ2, and the variance of εi is the sum of these variances over all N constraints (13). Note that the noise variance is only affected by the number of constraint violations, not by the weights on the constraints.
- (13)
The variance of the difference between εa and εb would be the sum of their variances, but shared violations cancel out because they involve the same value of nk for the shared constraint. For example, in (12) εa = –n1– n3, and εa = –n2 – n3, so εb – εa = –n1 – n2 because the n3 terms cancel out. So the variance of this difference d is 2σ2, and its standard deviation is √2σ. Thus the variance of d is equal to the sum of the squared differences in constraint violations between candidates a and b, multiplied by σ2, as in (14). As a result, the variance of d differs between candidate pairs, unlike in MaxEnt. For example, if we remove the violation of C2 from candidate b in (12) then the variance of d drops to σ2, and if we remove the violation of C3 from the same candidate, then the variance of d increases to 3σ2.
- (14)
- Variance of d in NHG
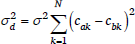
Since the noise difference d follows a normal distribution in NHG, Fd is the normal cumulative distribution function, Φ, but to map the distribution of d onto the standard normal distribution with standard deviation of 1, it is necessary to divide by σd, the standard deviation of d, so the probability of candidate a being selected depends on the harmony difference divided by σd (15). That is, the greater the noise that is added to the harmony difference between two candidates, the greater the probability that the noise reverses that harmony difference. So the measure of harmony difference that determines candidate probabilities is the number standard deviations of the noise difference, σd, that separate the harmony scores of the two candidates.
- (15)
The inverse of the normal cumulative distribution, Φ–1, is called the probit function. If we apply this function to both sides of (15), we obtain (16).
- (16)
Comparing (10) and (16), the expressions relating candidate probabilities to candidate harmonies in MaxEnt and NHG, respectively, we can see that in both cases the relative probabilities of two candidates depends on the difference in their harmonies, ha – hb, as established by the general analysis in (8). However, there are two differences that follow from differences in the distribution of d in the two frameworks: First, the harmony difference is related to Pa by different functions, logit in MaxEnt and probit in NHG. Second, Pa depends only on the harmony difference in MaxEnt, but in NHG it also depends on σd, which in turn depends on the sum of the squared violation differences of the two candidates (14).
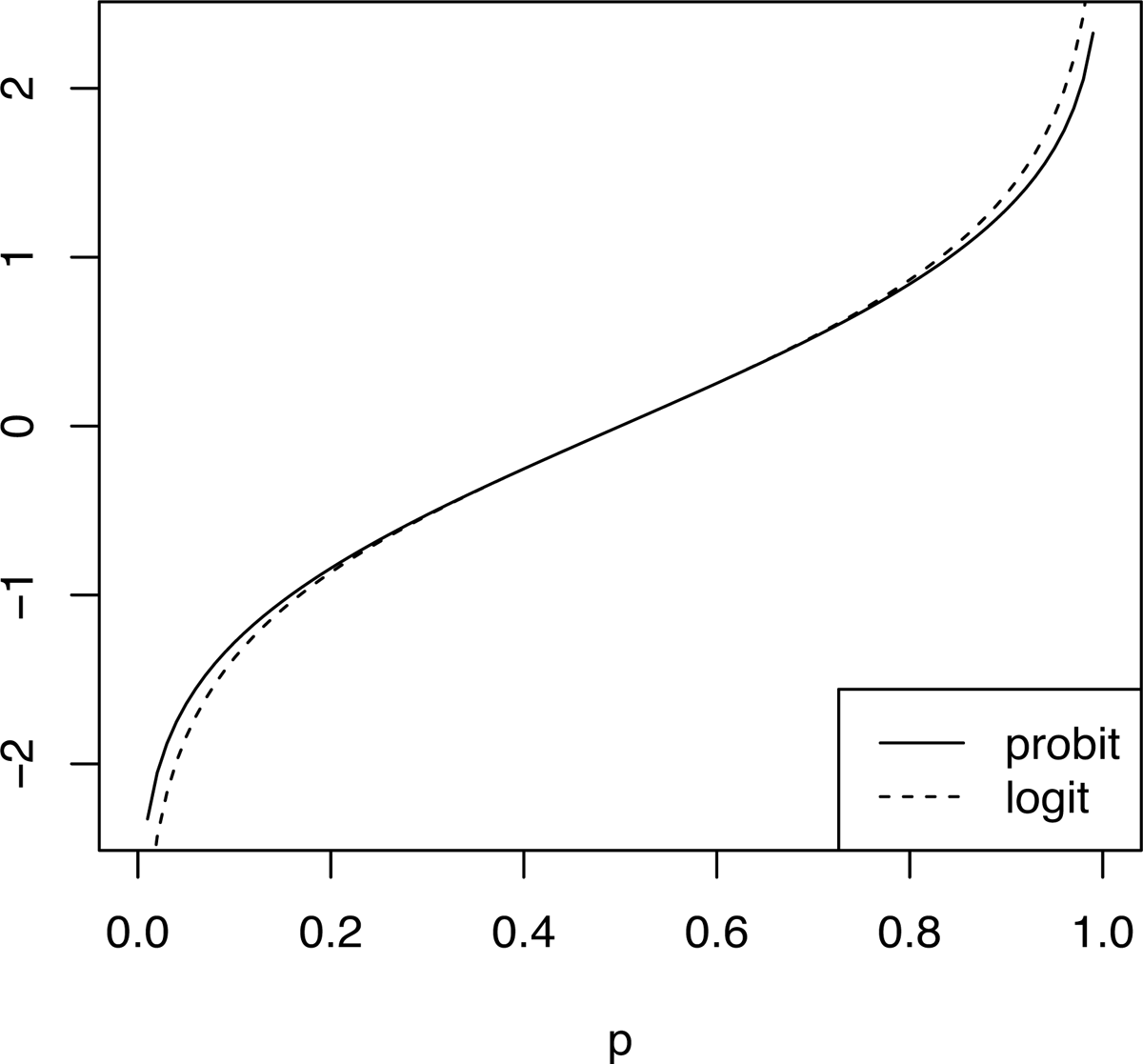
The second difference is the more important – we will show that it leads to testable predictions regarding the effects on the relative probabilities of a pair of candidates of changing some of their constraint violations. The first difference is relatively minor because the logit and probit functions are very similar (Figure 4), but we can investigate the contribution of this difference by adding to our comparison a variant of MaxEnt in which normal noise is added to candidate harmonies rather than Gumbel noise (cf. Hayes 2017).
In MaxEnt with normal noise the εi are drawn from identical normal distributions with variance σ2. Since the difference between two normal random variables is also normal, the noise difference d also follows a normal distribution, but the variance of this distribution, σd2, is 2σ2, because the variance of the difference between two normal random variables is equal to the sum of their individual variances. Since d follows a normal distribution, Fd is the normal cumulative distribution function, Φ, but to map the distribution of d onto the standard normal distribution with standard deviation of 1, it is necessary to divide by σd, i.e. 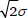 , so the probability of candidate a being selected is given by (17), and harmony is related to candidate probabilities via the probit function (18), as in NHG. So, comparing (18) to (16), we can see that the only difference from NHG lies in the fact that σd is the same for all pairs of candidates, whereas σd depends on the pattern of constraint violations in NHG. We will refer to this model as ‘normal MaxEnt’.1
, so the probability of candidate a being selected is given by (17), and harmony is related to candidate probabilities via the probit function (18), as in NHG. So, comparing (18) to (16), we can see that the only difference from NHG lies in the fact that σd is the same for all pairs of candidates, whereas σd depends on the pattern of constraint violations in NHG. We will refer to this model as ‘normal MaxEnt’.1
- (17)
- (18)
We will see that normal MaxEnt is similar to MaxEnt, as expected, but the difference between the logit and probit functions at probabilities close to 0 and 1 is large enough to result in significant differences in fits to data. We will also see in section 9 that there are further differences that become apparent in cases where there are three or more variant realizations for a given input, but those predictions will not be tested here since we do not have relevant data.
Before we draw out the predictions that follow from this analysis of MaxEnt and NHG, it is important to clarify that we have only analyzed the relationship between harmony and probability for a pair of candidates. We will see in section 9 that this analysis provides the building blocks for calculating the probability of a candidate winning over any number of competitors, but we defer that discussion because the current analysis is sufficient for tableaux in which only two candidates have probabilities significantly greater than zero, and that is true of our test case, which concerns the probabilities of forms with and without a schwa. Even if a tableau contains many candidates, if all but two of those have sufficient constraint violations that their probability is effectively zero, then all of the probability mass is divided between the two remaining candidates, and the other candidates are irrelevant to the calculation of their probabilities.
6. Variable realization of schwa in French
At this point it is useful to introduce the data that will be used to test the distinct predictions made by MaxEnt and NHG so we can use those data to exemplify the predictions. The data are from an experiment reported in Smith & Pater (2020), studying variable realization of schwa in French. Specifically, they investigated the probability of pronouncing the parenthesized schwa in the eight contexts in (19). These materials cross three factors that have been reported to affect the probability of schwa realization: (i) whether the schwa site is final in a clitic (e.g. [t(ə)]) or word (e.g. [bɔt(ə)]), (ii) whether the schwa site is preceded by one or two consonants, and (iii) whether the schwa site is followed by a stressed syllable or an unstressed syllable. Subjects were asked to identify their preferred pronunciation for orthographically presented phrases: with or without schwa. Previous research on French schwa indicates that this kind of judgment accurately reflects production patterns (Racine 2008). 27 subjects rated 6 items for each context.
- (19)
- Environments for schwa realization studied by Smith & Pater (2020)
Context: clitic-final /ə/ word-final /∅/ C_σ́ eva t(ə) 'ʃɔk
‘Eva shocks you’yn bɔt(ə) 'ʒon
‘a yellow boot’CC_σ́ mɔʁiz t(ə) 'sit
‘Maurice cites you’yn vɛst(ə) 'ʒon
‘a yellow jacket’C_σσ́ eva t(ə) ʃɔ'kɛ
‘Eva shocked you’yn bɔt(ə) ʃin'waz
‘a Chinese boot’CC_σσ́ mɔʁiz t(ə) si'tɛ
‘Maurice cited you’yn vɛst(ə) ʃin'waz
‘a Chinese jacket’
Smith & Pater’s analysis of schwa realization in these contexts involves the constraints in (20)–(23), together with Max and Dep, as illustrated by the tableaux in (24)–(28).
| (20) | NoSchwa: | Assign one violation for every [ə] in the output. |
| (21) | *CCC: | Assign one violation for every sequence of three consonants. |
| (22) | *Cluster: | Assign one violation for every sequence of two or more consonants. |
| (23) | *Clash: | Assign one violation for every two adjacent stressed syllables. |
The most general constraints in Smith & Pater’s analysis are *Cluster, which penalizes the consonant clusters that result in all items in (19) if schwa is not realized, and NoSchwa, which penalizes all instances of schwa. Additional constraints are required to account for differences in the probability of schwa realization across contexts.
Final schwa is realized more frequently in clitics than in full words. Smith & Pater analyze this difference as following from the schwa being underlying in the clitic, whereas it is epenthetic in word-final position, consequently Max favors realization of schwa in clitics, but not word-finally, whereas Dep penalizes realization of word-final schwa, but not clitic-final schwa (e.g. (24) vs. (25)).
Schwa is realized more frequently in the context CC_C, where it is preceded by two consonants, than in C_C, where it is preceded by only one. This is attributed to a constraint *CCC, which penalizes the triconsonantal cluster that results from non-realization of schwa in the former context ((28)  ), but not the latter ((26)
), but not the latter ((26)  ).
).
Schwa is also realized more frequently when the following word is a monosyllable rather than a disyllable (bɔtə'ʒon > bɔtəʃin'waz). Smith & Pater attribute this to clash avoidance: since stress falls on the last non-schwa vowel in a word, non-realization of schwa results in adjacent stressed syllables when the following word is a monosyllable (['bɔt'ʒon]), but not if it is a disyllable (or longer) (['bɔtʃin'waz]), e.g. (26) vs. (25). Adjacent stressed syllables are penalized by *Clash.
- (24)
- /ə/, C_σσ́

- (25)
- /∅/, C_σσ́

- (26)
- /∅/, C_σ́

- (27)
- /∅/, CC_σσ́

- (28)
- /∅/, CC_σ́

Smith & Pater’s data set provides a good testing ground for distinguishing MaxEnt from NHG because the factorial design of the experiment allows us to compare many pairs of tableaux that differ minimally in their constraint violations, and these frameworks make distinct predictions concerning the relationship between candidate probabilities across such pairs of tableaux, as is shown in the next section.
Our starting point for analysis follows Smith & Pater, but we will also consider variants of their analysis. In particular we consider analyses that eliminate redundancies from their constraint set. For example, Smith & Pater follow standard practice in positing separate Dep and Max constraints, so clitics and words are always differentiated by both of these constraints (clitics without schwa violate Max while words without schwa do not, and words with schwa violate Dep while clitics with schwa do not, e.g. (24) vs. (25)). This redundancy can be eliminated by replacing these two constraints by a single constraint that penalizes correspondence between schwa and zero, whether that correspondence results from epenthesis or deletion. We will also consider an expanded constraint set, motivated by the failure of the initial constraint set to account for all of the patterns observed in the data.
These alternative constraint sets encompass some competing analyses of the distribution of schwa in French. For example, it has been argued that schwa at clitic boundaries is epenthetic just like schwa at word boundaries (e.g. Côté 2000), in which case Max cannot be used to account for the higher rate of realization of schwa at clitic boundaries. Côté proposes that this effect is instead due to a constraint requiring ‘every morpheme to conform to a minimal CV form’ (p.108). This constraint would take the place of Max in the tableaux presented here, with exactly the same pattern of violations, but Dep violations would no longer differentiate words from clitics, so these contexts are distinguished by violations of a single constraint under this analysis. For the data under consideration here, this analysis makes exactly the same predictions as the variant of Smith & Pater’s analysis that collapses Max and Dep into a single constraint.
We will now use Smith & Pater’s data and analysis to illustrate the implications of the difference between MaxEnt and NHG demonstrated in section 5.
7. The effect on candidate probabilities of adding constraint violations
The implications of the difference between MaxEnt and NHG can be seen by considering the effect of adding or subtracting constraint violations from a tableau. We will see that in MaxEnt a given change in constraint violations always has the same effect on logit(Pcand), regardless of what other constraint violations are present in the tableau, whereas in NHG the effect of a change in constraint violations on probit(Pcand) depends on the violation pattern in the whole tableau.
7.1 Maxent grammar
Consider a tableau with two candidates a and b with harmonies ha and hb, and a second tableau which is identical except candidate b incurs an additional violation of one constraint. This additional violation means that the harmony of candidate b is hb – w, where w is the weight of the violated constraint. Given the analysis of MaxEnt grammar in the previous section (10), we know that in tableau one, logit(Pa) = ha – hb, and in tableau two, logit(Pa) = ha – (hb – w) = ha – hb + w. In other words, adding a constraint violation to candidate b increases the harmony difference by the weight of that constraint, w, and thus increases logit(Pa) by the same amount. Crucially this result is independent of all of the other constraint violations in the pair of tableaux, as long as they are the same in both tableaux. So MaxEnt predicts that adding a constraint violation to a tableau will always have the same effect on logit(Pa).
We can see how this analysis applies to the French schwa data by considering pairs of tableaux such as those in (24)–(28), above. We will refer to the candidates in these tableaux as the ə candidate and the ∅ candidate. The pairs of tableaux (25)–(26) and (27)–(28) are identical except that in the second tableau of each pair, the ∅ candidate incurs an additional violation of *Clash. This increases hə – h∅ by the weight of *Clash, w3, and thus increases logit(Pə) by the same amount, so MaxEnt predicts that the difference in logit(Pə) between (25) and (26) should be equal to the difference between (27) and (28).
The relevant information in these tableaux is more succinctly represented in a difference tableau, which records the constraint violations of the ə candidate minus those of the ∅ candidate. For example, the difference tableaux corresponding to (25) and (26) are shown in (29) and (30), with illustrative constraint weights. The harmony difference hə – h∅ increases by 0.6, the weight of *Clash, between (29) and (30). The harmony difference is the only information needed to calculate Pə in MaxEnt, and the differences in constraint violations are the additional information required to calculate Pə in NHG, as will be illustrated shortly. A negative harmony difference, hə – h∅, means that the schwa candidate has a lower harmony, and thus is less probable than the ∅ candidate, whereas a positive harmony difference means that the schwa candidate has a higher harmony, and thus is more probable.
- (29)
- /∅/, C_σσ́

- (30)
- /∅/, C_σ́

The same reasoning generalizes to pairs of tableaux that each differ in violations of a set of constraints. For example, pairs of tableaux for words and clitics in the same context differ in violations of both Max and Dep, as in (31) and (32). With words (31, 33), schwa is epenthetic so the schwa candidate violates Dep, while with clitics (32, 34) the schwa is underlying so the schwa candidate does not violate Dep, but the schwaless candidate violates Max, so in terms of difference tableaux, (32) and (34) add 1 to each of Max and Dep compared to (31) and (33), respectively. This increases the harmony difference hə – h∅ by the sum of the weights of these two constraints, i.e. 1 + 1.2 = 2.2, and thus increases logit(Pə) by the same amount. So MaxEnt predicts that the difference in logit(Pə) between word-final and clitic final positions should be the same in each context (C_σ́ and C_σσ́).
- (31)
- /∅/, C_σ́

- (32)
- /ə/, C_σ́

- (33)
- /∅/, C_σσ́

- (34)
- /ə/, C_σσ́

Smith & Pater’s data set provides several comparisons of these kinds. The table in (35) summarizes the difference tableaux for all eight contexts. It can be seen that four pairs differ by adding 1 to the difference in *Clash violations, 1-2, 3-4, 5-6, 7-8, so MaxEnt predicts that the difference in logit(Pə) should be the same for all of those pairs. Four pairs differ by +1 in *CCC and –1 in *Cluster, 1-3, 2-4, 5-7, 6-8, and four pairs differ by +1 in Max and Dep, 1-5, 2-6, 3-7, 4-8.
- (35)
- Difference tableaux for all contexts
NoSchwa *CCC *Clash Max Dep *Cluster 1 /∅/, C, _σσ́ –1 0 0 0 –1 +1 2 /∅/, C, _σ́ –1 0 +1 0 –1 +1 3 /∅/, CC, _σσ́ –1 +1 0 0 –1 0 4 /∅/, CC, _σ́ –1 +1 +1 0 –1 0 5 / ə /, C, _σσ́ –1 0 0 +1 0 +1 6 / ə /, C, _σ́ –1 0 +1 +1 0 +1 7 / ə /, CC,_σσ́ –1 +1 0 +1 0 0 8 / ə /, CC, _σ́ –1 +1 +1 +1 0 0
7.2 Noisy Harmonic Grammar
NHG does not predict that adding or subtracting a constraint violation should always have the same effect on candidate probabilities because changing constraint violations alters both the harmony difference hə – h∅, and the variance of the noise difference σd2, and Pə depends on both, as shown above (16, repeated here as 36). The variance σd2 depends on the sum of squared violation differences (14, repeated here as 37).
- (36)
- (37)
- Variance of noise difference d in NHG
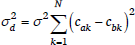
If we start from a tableau where the harmony difference is hə – h∅ and the standard deviation of d is σd, and then change some constraint violations, the harmony difference changes by Δh, and the variance of d can change to σd'. The resulting change in probit(Pə) is given by the expression in (38a), which can be rearranged to yield (38b), where the first term represents the effect of changing σd, while the second represents the effect of the change in harmony difference, Δh.
- (38)
- Change in probit(Pə) resulting from changes in hə – h∅ and σd (NHG)
- (a)
- (b)
For example, consider the tableaux in (29) and (30). The harmony difference in (29) is –2.2 and, assuming that the variance of the noise added to constraint weights, σ2, is 1, then σd2 is 3 – the sum of the squared differences in constraint violations – and σd is 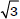 . (30) differs from (29) by adding a *Clash violation, increasing the harmony difference by 0.6, the weight on *Clash, so Δh = 0.6. However the additional constraint violation also increases σd'2 to 4 (σ'd = 2). Plugging these values into (38) yields an increase in probit(Pə) of 0.47.
. (30) differs from (29) by adding a *Clash violation, increasing the harmony difference by 0.6, the weight on *Clash, so Δh = 0.6. However the additional constraint violation also increases σd'2 to 4 (σ'd = 2). Plugging these values into (38) yields an increase in probit(Pə) of 0.47.
Another pair of tableaux that differ by a single *Clash violation, (39) and (40), show a smaller increase in probit(Pə) of 0.23 although the change in harmony is the same (Δh = 0.6) and σd and σ'd are the same (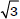 and 2, respectively). This is because the first term in (38b) depends on the initial harmony difference, hə – h∅, and this differs across the two pairs: –2.2 in (29), but 0.8 in (39). So for pairs of tableaux where MaxEnt predicts uniform differences in logit(Pə), NHG predicts systematic variation in differences in probit(Pə).
and 2, respectively). This is because the first term in (38b) depends on the initial harmony difference, hə – h∅, and this differs across the two pairs: –2.2 in (29), but 0.8 in (39). So for pairs of tableaux where MaxEnt predicts uniform differences in logit(Pə), NHG predicts systematic variation in differences in probit(Pə).
- (39)
- /∅/, CC_σσ́

- (40)
- /∅/, CC_σ́

In summary, we have seen that MaxEnt and NHG make distinct predictions concerning the effect on candidate probabilities of adding or subtracting constraint violations. In MaxEnt, the effect on logit(Pi) is always the same regardless of what other constraints are violated in the tableau, whereas in NHG the effect on probit(Pi) varies depending on the difference in harmony between the candidates before constraint violations are added or subtracted and the number of constraint violations in the tableaux.
We will test these predictions against Smith & Pater’s experimental data on the rate of realization of schwa in French. However, before turning to these tests we need to add one more form of stochastic HG to the comparison because many researchers who have adopted NHG have employed a variant of NHG in which the noise added to constraint weights is prevented from making those weights negative, so it is important to analyze the properties of this framework as well.
7.3 Noisy Harmonic Grammar with censored normal noise
The final stochastic grammar model that we will consider is a variant of NHG with a non-normal noise distribution. This variant is motivated by a desire to prevent noise making constraint weights negative. Adding normal noise to a low constraint weight can easily result in a negative weight, and this effectively reverses the constraint, favoring the configurations that it is supposed to penalize. It is also necessary to ensure that noise cannot make constraint weights less than or equal to zero for harmonically bounded candidates to be assigned zero probability (Jesney 2007; Hayes 2017). Accordingly, a number of researchers have adopted a variant of NHG in which negative constraint weights are replaced by 0 (e.g. Smith & Pater 2020). This means that the nk noise terms added to constraint weights follow censored normal distributions, in which the noise added to a constraint with weight w follows a normal distribution in which values at or below –w are replaced by 0. For low constraint weights, this results in a density function with a substantial spike at the lower bound of the distribution (Figure 5).
Summing censored normal random variables results in εi and d with complex distributions, making the resulting model difficult to analyze mathematically. However, in practice d is approximately normal, and, as in normal NHG, its variance depends on the summed squared differences in constraint violations between the two candidates, so the model makes qualitatively similar predictions to normal NHG. We will refer to this variant of NHG as ‘censored NHG’.
One novel feature of this model that turns out to have considerable importance is that the variance of d does not only depend on the number of constraint violations, it also depends on the weights of those constraints because the noise added to constraints with lower weights is more severely censored, and therefore has lower variance. For example, the distributions in Figure 5 are based on a normal distribution with standard deviation of 1, but the censored distribution on the left has standard deviation 0.98 and that on the right has standard deviation 0.74.
8. Testing the predictions
We test the predictions outlined in the previous section against Smith & Pater’s data on the probability of realizing schwa in a variety of contexts in French. First, we ask which predictions are best supported by the data, by comparing the overall fit of grammars in each framework, and by probing how well the specific predictions are supported. However, this process reveals that even the best grammars fail to account for significant patterns observed in the data, motivating the addition of a constraint to the analysis. A second round of comparisons using this revised constraint set leads to the conclusion that the predictions of MaxEnt are best supported, although censored NHG also fits the data well.
8.1 Fitting the models to the data
We want to test the performance of the various stochastic Harmonic Grammars as grammar frameworks, independent of the performance of any learning algorithms that might be proposed to learn constraint weights in that grammar framework, so it is important to compare the grammars that provide the best fit to the data. For example, our conclusions differ somewhat from Smith & Pater (2020) concerning the relative performance of MaxEnt and censored NHG on the schwa data because Smith & Pater relied on a learning algorithm for censored NHG that appears not to have arrived at the best-fitting grammar.
Our criterion for goodness of fit is Maximum Likelihood (ML). That is, we searched for the constraint weights that maximize the probability of the data given that grammar model (e.g. Myung 2003). This is straightforward for the MaxEnt and normal MaxEnt grammars because, where there are only two candidates, MaxEnt is equivalent to a logistic regression model in which the probability of pronouncing schwa is predicted based on the differences in the violations of each constraint, and normal MaxEnt is equivalent to a probit regression model with the same structure, so ML constraint weights for these stochastic HGs were found using the glm function in R (R Core Team 2020).2
NHG does not correspond to a standard statistical model, but given constraint weights, it is straightforward to calculate candidate probabilities using equations (14) and (15), so standard optimization algorithms can be used to search for the ML constraint weights. We used the Nelder-Mead algorithm, as implemented in the optim function in R.
Censored NHG is more problematic because it is not possible to calculate candidate probabilities – they have to be estimated through simulation. However, with one million simulations per grammar it was possible to obtain probability estimates that were sufficiently stable to search for ML constraint weights using the Nelder-Mead algorithm. This process was slow, but was able to find substantially better constraint weights than those found by Smith & Pater using the HG-GLA algorithm (Boersma & Pater 2016) with 400,000 samples from the experimentally observed distribution.3
The results are summarized in Tables 1 and 2. Table 1 shows the ML constraint weights for all of the models under consideration. For the MaxEnt and normal MaxEnt grammars the standard deviations of the εi are standard for the relevant distributions (π/√6 for Gumbel, 1 for Normal). For NHG and censored NHG the standard deviation of the noise added to constraint weights, nk, is set to 1, although in censored NHG this is the standard deviation of the underlying normal distribution before censoring.4
ML constraint weights for the stochastic HGs described in the text.
| MaxEnt | Normal MaxEnt | NHG | Censored NHG | |
|---|---|---|---|---|
| NoSchwa | 2.08 | 1.68 | 2.20 | 11.23 |
| *CCC | 2.84 | 2.29 | 2.98 | 12.02 |
| *Clash | 0.48 | 0.39 | 0.57 | –0.04 |
| Max | 2.14 | 1.69 | 2.21 | 1.96 |
| Dep | 0 | 0 | 0 | –1.32 |
| *Cluster | 0 | 0 | 0 | 9.43 |
Observed probabilities of pronouncing schwa in each context, and fitted probabilities from each stochastic HG.
| Fitted probabilities | |||||
|---|---|---|---|---|---|
| Context | Pə | MaxEnt | Normal MaxEnt |
NHG | Censored NHG |
| /∅/, C, _σσ́ | 0.09 | 0.11 | 0.12 | 0.10 | 0.10 |
| /∅/, C, _σ́ | 0.12 | 0.17 | 0.18 | 0.21 | 0.17 |
| /∅/, CC, –σσ́ | 0.68 | 0.68 | 0.67 | 0.67 | 0.70 |
| /∅/, CC, _σ́ | 0.83 | 0.78 | 0.76 | 0.75 | 0.77 |
| /ə/, C, _σσ́ | 0.56 | 0.52 | 0.50 | 0.50 | 0.54 |
| /ə/, C, _σ́ | 0.65 | 0.63 | 0.61 | 0.61 | 0.62 |
| /ə/, CC, _σσ́ | 0.91 | 0.95 | 0.95 | 0.96 | 0.95 |
| /ə/, CC, _σ́ | 0.94 | 0.97 | 0.97 | 0.96 | 0.96 |
| deviance | 14.6 | 21.7 | 26.0 | 12.8 | |
The MaxEnt and NHG grammars have 0 weights for two constraints, Dep and *Cluster. That is because the full constraint set is redundant given these grammar models. As can be seen from (35), the difference score for *Cluster is equal to 1 minus the difference score for *CCC in the schwa data, and the difference score for Dep is equal to the difference score for Max minus 1. Since the harmony difference is a linear function of these difference scores, these redundancies means that there are an infinite number of ways to derive any particular set of harmony differences between candidates. To ensure that there is a unique best-fitting set of constraint weights, this redundancy was eliminated by setting the weights of Dep and *Cluster to 0. Note that setting these weights to 0 in NHG does not mean that the constraints have no effect on the outcome, because they are still perturbed by noise and therefore can be non-zero in any particular evaluation.
Dep and *Cluster are not redundant in censored NHG because in that model the weights of constraints affect the variance of the noise that they add to candidate harmony, as discussed further below. In addition, removing *Cluster would make the realization of schwa harmonically bounded word-finally in C_σσ́ (25), which would mean that censored NHG would incorrectly assign a zero probability to schwa in this context.
A second point to observe is that the censored NHG grammar has constraints with negative weights (*Clash and Dep). These negative weights do not actually reverse the effects of these constraints because the constraint weights are not permitted to remain negative after the addition of noise. In this model negative weights represent censoring of more than half of the noise distribution, so constraint weights are drawn from a narrow distribution with a spike at 0. Some implementations of censored NHG also require constraint weights to be non-negative before addition of noise, e.g. Smith & Pater (p.25). This restriction would result in a poorer fit to the data here.
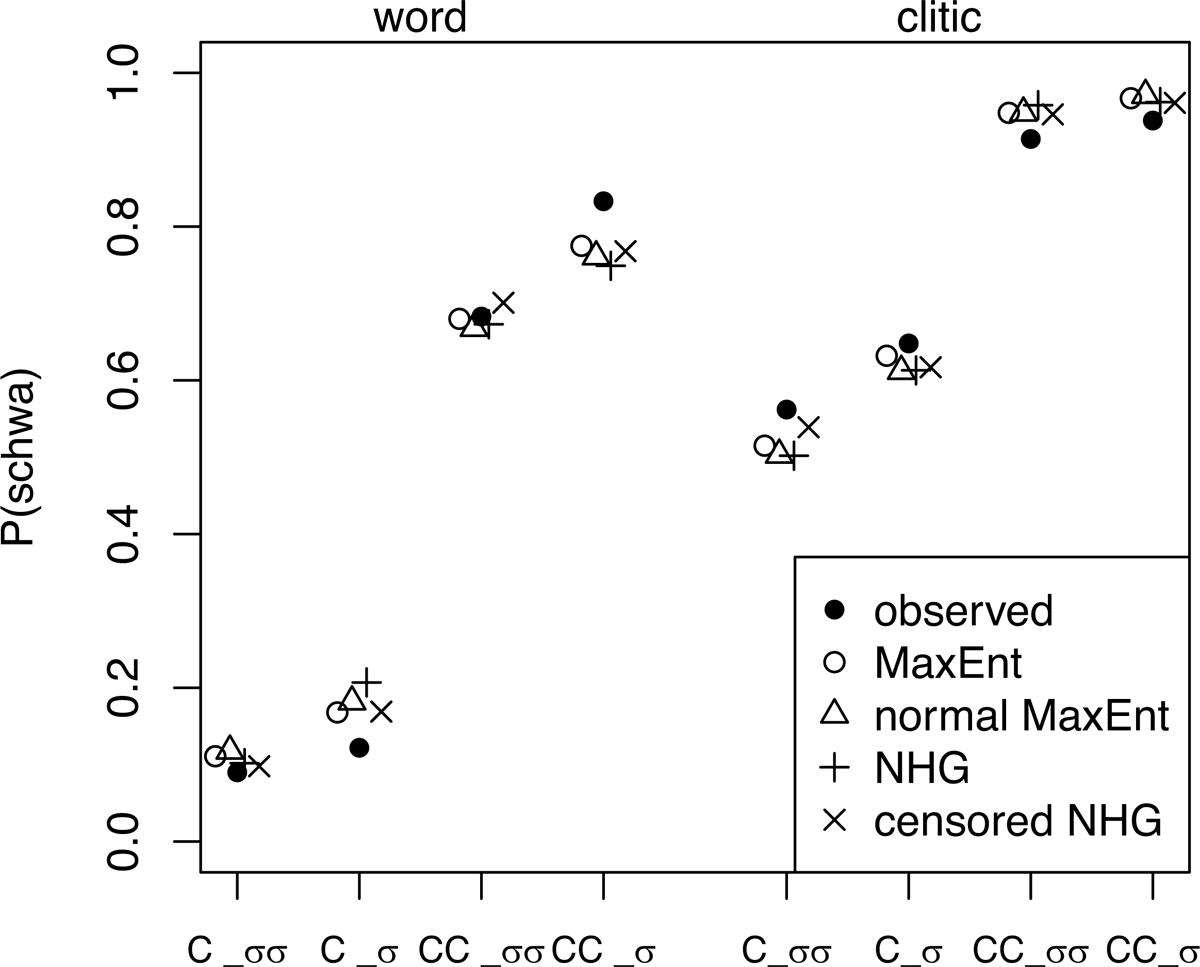
The performance of the different grammars is summarized in Table 2, which compares the observed probability of pronouncing schwa in each context to the fitted probabilities derived from each grammar. The overall goodness of fit of each grammar is measured by the deviance, which is directly related to log-likelihood (lower deviance indicates better fit).5 Maxent and censored NHG perform similarly (deviances 12.8 and 14.6), while normal MaxEnt performs worse, and the worst fit is obtained with normal NHG.
8.2 Evaluating the fit of the grammars
A common way to compare models is in terms of their AIC values (Burnham & Anderson 2002), which is –2 × log-likelihood plus a penalty equal to twice the number of parameters in the model (in this case the number of constraint weights), so lower values are better. If models have the same number of parameters then the difference in AIC (ΔAIC) between two models is equal to the difference in their deviances, so ΔAIC of MaxEnt and Normal MaxEnt is 7.1. According to Burnham & Anderson (2002: 70ff.) this indicates that Normal MaxEnt has ‘considerably less support’ than regular MaxEnt, so in spite of the similarity between these models, the difference between the logit and probit functions is meaningful here. NHG has an AIC more than 10 higher than MaxEnt, which means it has ‘essentially no support’.
Comparisons between MaxEnt and censored NHG are more complicated. As discussed above, the MaxEnt models make use of only four of the six constraints in Table 1 because the full constraint set is redundant for these models, so in one sense censored NHG has two additional parameters compared to the MaxEnt models and normal NHG, and thus its AIC value should include a penalty of 2 × 2 = 4. However, the constraints are hypothesized to be universal, so it might be argued that censored NHG should not be penalized if it can make use of all of the constraint weights while the other grammars cannot. However, we will see below that the censored NHG grammar is effectively using the redundant constraints to vary the noise variance across conditions, and this would not be possible if other data were added that made the additional constraints non-redundant, so this model really does have additional parameters compared to the other models.
Whether censored NHG is penalized for additional parameters or not, the conclusions are similar. With the complexity penalty, MaxEnt has the lowest AIC, but the AIC of censored NHG is only 2.2 higher, and Burnham & Anderson (2002) describe models within 2 of the best model as having ‘substantial support’. Without the complexity penalty, censored NHG is the best model, but the AIC of MaxEnt is only 1.8 higher.
So in terms of AIC, MaxEnt and censored NHG are similar. Normal MaxEnt is substantially worse than the closely comparable MaxEnt model, and normal NHG is clearly the worst model. However, it is revealing to look more closely at the details of the model fits and how they relate to the distinct predictions laid out in section 7.
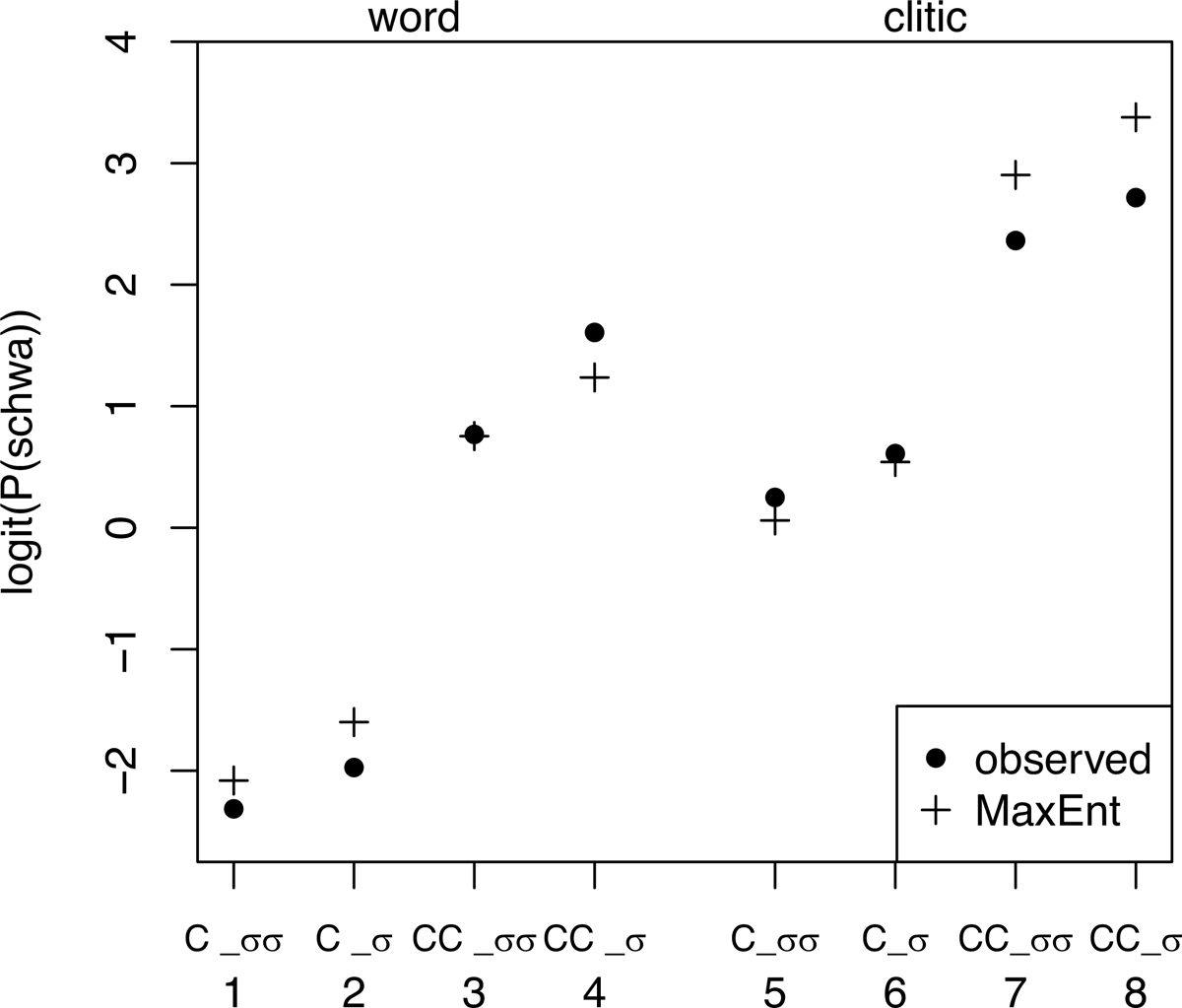
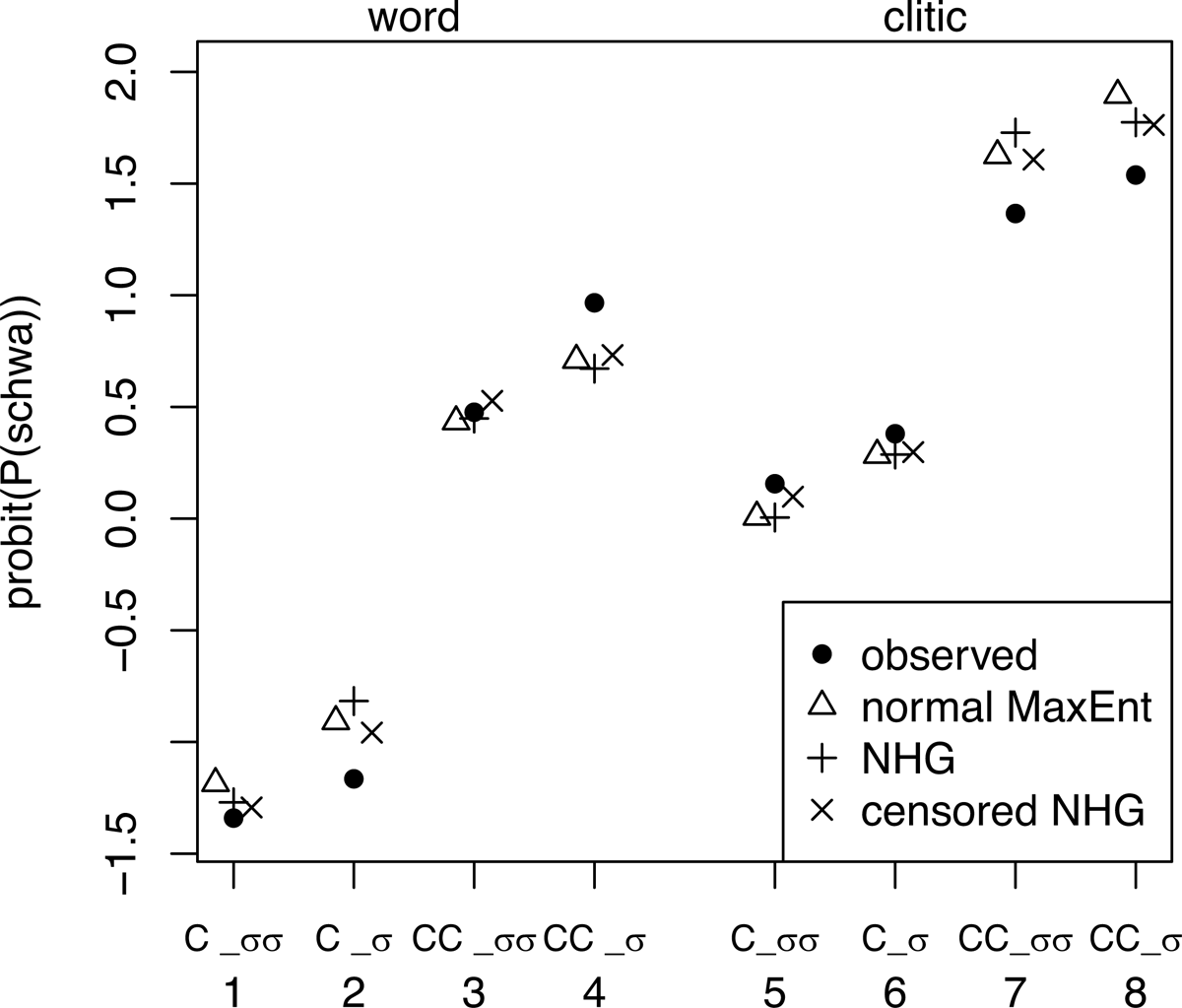
The observed probabilities of pronouncing schwa in each of the eight contexts are compared to the fitted probabilities from the models in Figure 6. However, it is more instructive to look at logit(Pə) for MaxEnt (Figure 7), and probit(Pə) for stochastic HGs with normal, or approximately normal, noise (Figure 8), because the predictions that we seek to test concern these quantities.
The analysis in section 7 demonstrated that MaxEnt predicts that all pairs of contexts that differ in the same constraint violations should show the same difference in logit(Pə). So adjacent pairs of points in Figure 7 (1-2, 3-4, 5-6, 7-8) should be separated by the same vertical distance because they differ only in one *Clash violation, and the same should apply to pairs 1-3, 2-4, 5-7, 6-8, which differ only in preceding context (CC vs. C_), and thus in violations of *CCC and *Cluster, and to pairs 1-5, 2-6, 3-7, 4-8, which differ in Max and Dep violations.
Examination of the data in Figure 7 indicates that most of these predictions are quite well supported, except for the effect of changing *CCC and *Cluster violations (CC_ vs. C_), which differs substantially between deletion and epenthesis contexts. That is, the effect is smaller for clitics (the right half of the figure) than for words (the left half of the figure), so the differences between 1 and 3, and 2 and 4 are larger than the differences between 5 and 7, and 6 and 8.
These visual impressions can be confirmed statistically. In a logistic regression model of Pə with violation differences as predictors, significant deviations from the predictions of MaxEnt correspond to significant interactions between constraints. In a model including all two-way interactions between constraints, the only significant interaction is between MAX and *CCC. Consequently, the MaxEnt model provides a good fit to most of the data, but overestimates the difference between CC_ and C_ pairs in deletion contexts (5-7, 6-8), and underestimates them in epenthesis contexts (1-3, 2-4), because it necessarily predicts the same difference between all of these pairs.
Normal MaxEnt makes similar predictions but with regard to probit(Pə). Figure 8 shows a similar picture to Figure 7, which is unsurprising given the similarities between the logit and probit functions. But it turns out that the predictions hold less well for probit(Pə) than for logit(Pə), so the MaxEnt analysis provides a better fit to the schwa data.
NHG predicts systematic variation in differences in probit(Pə) between pairs of contexts that differ in the same constraint violations. Specifically, we have seen that the change in probit(Pə) that results from adding and subtracting constraint violations in normal NHG is given by (38), repeated here as (41), where hə – h∅ is the harmony difference before the change, Δh is the change in the harmony difference, and σd and σd' are the standard deviations of the noise difference before and after the change.
- (41)
- Change in probit(Pə) resulting from changes in hə – h∅ and σd in normal NHG
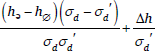
Table 3 shows the values required to calculate (41), hə – h∅ and σd, for each context. The variance of the noise difference d is the sum of the squared violation differences (14). Since violation differences are all +1 or –1 in the schwa tableaux (35), the variance is equal to the number of violation differences in the tableau, i.e. 3 or 4 depending on the context, and σd is the square root of the variance.
hə – h∅ and σd, for each context in normal and censored NHG. σd for censored NHG is estimated by simulation.
| normal NHG | censored NHG | ||||
|---|---|---|---|---|---|
| context | hə – h∅ | σd | hə – h∅ | σd | |
| 1 | /∅/, C, _σσ́ | –2.20 |
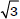 |
–1.84 | 1.43 |
| 2 | /∅/, C, _σ́ | –1.63 | 2 | –1.46 | 1.54 |
| 3 | /∅/, CC, _σσ́ | 0.77 |
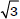 |
0.74 | 1.43 |
| 4 | /∅/, CC, _σ́ | 1.34 | 2 | 1.13 | 1.54 |
| 5 | / ə /, C, _σσ́ | 0.01 |
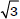 |
0.17 | 1.72 |
| 6 | / ə /, C, _σ́ | 0.58 | 2 | 0.56 | 1.81 |
| 7 | / ə /, CC,_σσ́ | 2.98 |
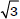 |
2.76 | 1.72 |
| 8 | / ə /, CC, _σ́ | 3.55 | 2 | 3.14 | 1.81 |
The adjacent contexts in Figure 8 (1-2, 3-4, 5-6, 7-8) differ by a *Clash violation incurred by the schwaless candidate, so Δh in each pair is the weight on *Clash, 0.57. Adding the additional difference in constraint violations increases σd from 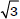 to 2, i.e. σ'd = 2 in each pair, so the second term in (41), Δh/σd', is the same in all of these pairs. However hə – h∅ differs across the pairs, so the value of the first term in (40) differs too. Specifically, since σd – σd' is negative (
to 2, i.e. σ'd = 2 in each pair, so the second term in (41), Δh/σd', is the same in all of these pairs. However hə – h∅ differs across the pairs, so the value of the first term in (40) differs too. Specifically, since σd – σd' is negative (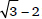 ), this term decreases as hə – h∅ increases, so the increases in probit(Pə) in these pairs are predicted to be ordered: 1-2 > 5-6 > 3-4 > 7-8. This is not empirically correct. In the experimental data, probit(Pə) increases by 0.2 for all of these pairs except 3 vs. 4, for which it increases by 0.5. Consequently NHG overpredicts the difference between 1 and 2, and underpredicts the difference between 7 and 8.
), this term decreases as hə – h∅ increases, so the increases in probit(Pə) in these pairs are predicted to be ordered: 1-2 > 5-6 > 3-4 > 7-8. This is not empirically correct. In the experimental data, probit(Pə) increases by 0.2 for all of these pairs except 3 vs. 4, for which it increases by 0.5. Consequently NHG overpredicts the difference between 1 and 2, and underpredicts the difference between 7 and 8.
Turning to pairs that differ only in whether their preceding context is CC_ or C_ (1-3, 2-4, 5-7, 6-8), the CC_ context adds 1 to the difference in *CCC violations while subtracting 1 from the difference in *Cluster violations, compared to the C_ context. This leaves the summed violation differences unchanged, so σd is the same for both tableaux, i.e. σd – σd'. This means that the first term of (41) is 0, so the change in probit(Pə) depends only on Δh and σd. Δh is equal to the difference between the weights on *CCC and *Cluster, 3.42 – 0.45 = 2.97, in all pairs, while σd is 2 for _σ́ pairs and 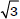 for _σσ́ pairs (Table 3), so the difference in probit(Pə) for these pairs is predicted to differ between _σ́ vs. _σσ́, but to be the same for words and clitics. These predictions are also incorrect: We have seen that the experimental results show a significantly smaller difference between CC_ and C_ contexts with clitics than with words where NHG predicts no difference, and small and inconsistent differences between _σ́ vs. _σσ́ contexts, where NHG predicts a bigger difference in _σσ́.
for _σσ́ pairs (Table 3), so the difference in probit(Pə) for these pairs is predicted to differ between _σ́ vs. _σσ́, but to be the same for words and clitics. These predictions are also incorrect: We have seen that the experimental results show a significantly smaller difference between CC_ and C_ contexts with clitics than with words where NHG predicts no difference, and small and inconsistent differences between _σ́ vs. _σσ́ contexts, where NHG predicts a bigger difference in _σσ́.
In summary, the contextual variation in differences in probit(Pə) due to a change in constraint violations predicted by NHG is not supported by the experimental data: This grammar predicts variation where the data show uniformity, and fails to predict variation where it is actually observed. Consequently the NHG grammar provides the worst fit to the data.
While the formula for change in probit(Pə) (41) is not exact for censored NHG, it is a good approximation, so this model predicts qualitatively similar patterns to normal NHG. Given the poor performance of normal NHG, this raises the question why censored NHG is able to achieve a lower deviance than MaxEnt. The answer is that censoring the noise distribution means that variance of the noise contributed by a constraint decreases as the weight on that constraint decreases because more of the distribution is censored (Figure 5).
This phenomenon has two consequences: First, low-weighted constraints contribute less noise, so their effect on εi is much less than in normal NHG. This reduces the magnitude of some of the problematic effects predicted by normal NHG. For example, censored NHG also predicts that the effect on probit(Pə) of adding a *Clash violation should depend on hə – h∅, contrary to the experimental results. However the magnitude of the predicted variation is much smaller than with uncensored normal noise because *Clash is assigned a very low weight, which means violations of this constraint contribute relatively little noise. As a result the difference in (σd) between tableaux with and without a *Clash violation is small, as shown in Table 3, and thus the magnitude of the first term of (41) is small.
In addition, the presence of redundant pairs of constraints like Max and Dep mean that weight can be allocated between these constraints to manipulate εi as well as the harmonies of candidates. That is, the harmony difference, hə – h∅, for words and clitics in the same environment (e.g. ['bɔt(ə)'ʒon] and [e'vat(ə)'ʃɔk]) differ in violations of both Max and Dep: schwa after a word is epenthetic and thus violates Dep but not Max, while schwa is underlying in clitics, so failure to realize it violates Max but not Dep. So the difference in the probability of schwa in words and clitics in the same context is accounted for by the summed weights of Max and Dep. So in MaxEnt, any pair of weights that sums to the same value derives the same patterns, hence the redundancy. But in censored NHG, the weights of the constraints also determine the variance of the noise introduced by a violation of that constraint, so noise variance can be adjusted by adjusting the relative weights of Max and Dep. In the best fitting model, Max receives a weight of 0.394 while Dep receives a weight of –0.263, so Dep contributes very low-variance noise to tableaux that contain Dep violations, i.e. tableaux with underlying /∅/ (words). As a result, tableaux for words have lower σd than clitic tableaux with underlying /ə/ (Table 3), so words show a larger effect of differences in *CCC violations on probit(Pə) because the second term in (41), Δh/σd', is larger where σd' is smaller.
In summary, with censored NHG, it is possible to mitigate the bad predictions observed with normal NHG, and it is possible to use a redundant constraint to adjust noise variance to partially model some observed contextual variation in the effects of differences in constraint violations on probit(Pə). The net result is a slightly better fit to the data than can be achieved with MaxEnt. We can demonstrate the role played by the redundancy between Max and Dep in censored NHG’s performance by removing it: If Max and Dep are replaced by a constraint that penalizes correspondence between schwa and ∅ (i.e. a constraint that is violated if either Max or Dep would be violated), then the performance of NHG with censored normal constraint noise drops to the level of regular NHG, the worst model (deviance = 26).
It is clear from examination of both varieties of NHG that the distinctive predictions of these models about the ways in which the effect of adding or subtracting a constraint should depend on the pattern of violations in the rest of the tableau are not confirmed. Censored NHG is only able to compete with MaxEnt because it can exploit the redundancy between Max and Dep to systematically vary σd across tableaux, so a better test of the differences between MaxEnt and censored NHG would only compare tableaux that differ in a single constraint violation. Unfortunately, this is not possible with schwa/zero alternations because every comparison between schwa and zero candidates necessarily involves a difference in either Max or Dep violations.
Besides revealing the unanticipated effect of redundant constraints in censored NHG, this examination of the fit of the four stochastic HG’s suggests that none of them capture all of the significant patterns in the data. We have already noted that MaxEnt fails to capture a significance difference in the effect of *CCC/*Cluster violations on words vs. clitics, and we will see next that this true of all of the models under consideration, so the comparison thus far has been between incomplete analyses.
Given that this interaction effect is not successfully modeled in any of the frameworks, the source of the problem presumably lies in the constraint set: an additional constraint is required to fit the schwa data. We will see that comparison of the stochastic Harmonic Grammar frameworks with respect to this revised constraint set provides a better test of their predictions since the best models fit the data well and redundant constraints no longer contribute to the fit of the censored NHG model. The results provide support for MaxEnt over censored NHG, and the procedure illustrates methods that are generally applicable to the analysis of stochastic Harmonic Grammars.
8.3 Comparisons using a revised constraint set
Evaluating the adequacy of stochastic grammars is tricky. The condition for adequacy cannot be a precise match between observed and predicted probabilities because we expect mismatches between observed and predicted probabilities in any finite sample of data, even given the true grammar. Instead we want to determine when those mismatches are small enough to conclude that the grammar accounts for the data.
Here we adopt a standard statistical method for assessing the fit of a probability model to data, a Likelihood Ratio Test of lack of fit (Agresti 2007: 145ff.). In effect, this test assesses whether the fit of the grammar could be improved significantly by adding constraints to the analysis. Specifically, it compares the grammar to a ‘saturated’ model that has one constraint for each of the contexts under analysis and is thus able to fit the observed probabilities perfectly, achieving a deviance of 0, and estimates the probability that this reduction in deviance could be due to random correlations between the additional constraints and the observed probabilities. This analysis is applicable here given that our grammars were fitted by Maximum Likelihood Estimation, and the relevant test statistics are the deviance values presented in Table 2, with degrees of freedom equal to the number of extra parameters in the saturated model.
The test reveals that all of the grammars considered show significant lack of fit. For models with four constraint weights (and thus four residual degrees of freedom, given that we are analyzing eight contexts), the deviance threshold for significant lack of fit at p < 0.05 is 9.5 while for censored NHG with six constraint weights, the threshold is 6, and all of the grammars exceed these thresholds. In other words, the constraint set proposed by Smith & Pater is insufficient to fully account for the data in any of the grammar frameworks.
The main shortcoming of these grammars is that they fail to capture the fact that the difference in the probability of schwa candidates between C_ and CC_ contexts is smaller in clitics (with underlying /ə/) than in words (with underlying /∅/). Given the current constraint set, MaxEnt predicts that the difference in logit(Pə) between these contexts should be the same for both clitics and words. The only grammar that derives a difference in the right direction is censored NHG, but the modeled effect is not large enough to fit the data.
We can verify that this is the source of the problem by adding a constraint whose violation depends on both preceding context (CC_ vs. C_) and whether the form contains underlying /∅/ or /ə/, and showing that this makes it possible to formulate grammars that show no significant lack of fit. The additional constraint could take a variety of forms, but one possibility is a constraint that penalizes CCC clusters only if the entire cluster falls within the same intermediate phrase (iP), inspired by related constraints proposed by Côté (2000: 129ff., 159ff.).
This analysis posits that the relevant difference is not between clitics and words per se, but between the prosodic contexts in which they appear in the experimental materials. In the clitic sentences, potential clusters are split over the boundary between the subject and the VP (e.g. [mɔʁiz t(ə) si'tɛ] ‘Maurice cited you’), whereas in the sentences with lexical words, the cluster arises between a noun and adjective (e.g. 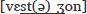 ‘yellow vest’). Studies by D’Imperio & Michelas (2014) and Michelas & D’Imperio (2015) indicate that the boundary between subject and VP is often an iP boundary, whereas DP-internal breaks are marked by Accentual Phrase boundaries. Assuming this prosodic difference applies to Smith & Pater’s materials, then a constraint *CCC/iP, penalizing triconsonantal clusters that fall within an iP, would only penalize CCC clusters in lexical words. This constraint adds to the effect of generic *CCC to derive the larger difference between C_ and CC_ items observed with epenthetic, word-final schwa compared to clitic schwa.
‘yellow vest’). Studies by D’Imperio & Michelas (2014) and Michelas & D’Imperio (2015) indicate that the boundary between subject and VP is often an iP boundary, whereas DP-internal breaks are marked by Accentual Phrase boundaries. Assuming this prosodic difference applies to Smith & Pater’s materials, then a constraint *CCC/iP, penalizing triconsonantal clusters that fall within an iP, would only penalize CCC clusters in lexical words. This constraint adds to the effect of generic *CCC to derive the larger difference between C_ and CC_ items observed with epenthetic, word-final schwa compared to clitic schwa.
Some support for the hypothesis that the effect is due to prosodic structure comes from Dell’s (1977) finding that word-final schwa is epenthesized into CCC clusters formed across Adjective-Noun boundaries at higher rates than in CCC clusters formed at Subject-VP boundaries.6 These data indicate that a similar effect is observed with materials that only involve words, not clitics, so the effect must be due to the difference in syntactic structure, or an associated difference in prosodic structure, as hypothesized here.
The ML constraint weights for grammars using this expanded constraint set are shown in Table 4, together with their deviance scores. Adding *CCC/iP to the constraint set eliminates the significant lack of fit in both MaxEnt and censored NHG, but not in normal NHG. The residual deviance of the revised MaxEnt grammar drops to 2.2, which is a significant improvement over the grammar without *CCC/iP (χ2(1) = 12.4, p < 0.001), and represents no significant lack of fit (χ2(3) = 2.2, p > 0.05). The deviance of the censored NHG grammar with *CCC/iP added drops to 4.6, which is a significant improvement over the original grammar (χ2(1) = 8.2, p < 0.01), but still shows significant lack of fit because it includes two more constraints than the MaxEnt grammar, Dep and *Cluster, and thus two fewer degrees of freedom for the goodness of fit test (χ2(1) = 4.6, p < 0.05). However, with *CCC/iP in the grammar, Max and Dep can be replaced by a single constraint that penalizes deletion or insertion of schwa with a slight decrease in residual deviance to 4.5, and this grammar shows no significant lack of fit (χ2(2) = 4.5, p > 0.05). This comparison further confirms that the only contribution of the redundant Max and Dep constraints in censored NHG did lie in adjusting the variance of the noise difference, σd2, to better fit the difference in the effect of *CCC in words vs. clitics which is now being better accounted for by *CCC/iP. In normal NHG, the enlarged constraint set results in a reduction in deviance to 6.7, which is unchanged by collapsing Max and Dep, and this is a little below the threshold for lack of fit (χ2(3) = 6.7, p > 0.05). It is also interesting to note that adding *CCC/iP more or less eliminates the difference in deviance between MaxEnt and normal MaxEnt (2.2 vs. 2.5).
ML constraint weights and deviances for grammars using the revised constraint set.
| MaxEnt | Normal MaxEnt | NHG | Censored NHG | |
|---|---|---|---|---|
| NoSchwa | 1.10 | 0.89 | 1.19 | 11.31 |
| *CCC | 2.12 | 1.68 | 2.18 | 12.25 |
| *CCC/iP | 1.18 | 1.09 | 1.62 | 1.55 |
| *Clash | 0.50 | 0.40 | 0.59 | 0.16 |
| Max.Dep | 1.28 | 1.07 | 1.41 | 1.29 |
| *Cluster | 0 | 0 | 0 | 10.24 |
| deviance | 2.2 | 2.5 | 6.7 | 4.5 |
The revised grammars provide a better test of the predictions of the different stochastic Harmonic Grammar models because the comparison set now includes grammars that fit the data well, and because the MaxEnt and NHG grammars are now distinguished by their fundamental predictions rather than by their ability to exploit constraints that happen to be redundant in the present data set. The revised MaxEnt grammar has lower deviance than the revised censored NHG grammar: 2.2 vs. 4.5. Since the NHG grammar still requires one more constraint than the MaxEnt grammar, *Cluster, the difference between the grammars in AIC is 4.3, where a difference greater than 4 is taken by Burnham & Anderson (2002) to indicate that the model with higher AIC has ‘considerably less support’, so this data set supports the predictions of MaxEnt over those of NHG, even in its censored normal variant.
8.4 Interim summary
In summary, we have tested a basic difference between MaxEnt and NHG against data on schwa realization in French: In MaxEnt, a given change in constraint violations always has the same effect on logit(Pcand), whereas in NHG, the effect of a change in constraint violations depends on the violation pattern in the whole tableau. We tested these predictions against Smith & Pater’s data on schwa realization in French, and the results support MaxEnt over NHG.
The predictions are most directly tested by the comparison between MaxEnt and normal MaxEnt on the one hand and regular NHG on the other, and NHG gives a substantially poorer fit to the data with both Smith & Pater’s original constraint set and with the augmented constraint set including *CCC/iP. MaxEnt differs from NHG not only in these basic predictions, but also in the function that relates probability to harmony: logit in MaxEnt and probit in NHG. This difference is eliminated in the comparison between normal MaxEnt and NHG, and the normal MaxEnt grammar still performs substantially better than NHG, especially with the augmented constraint set.
The comparison between MaxEnt and censored NHG introduces a third difference: censored NHG predicts that the relative probabilities of candidates should be affected by the weights of the constraints that show violation differences, because lower-weighted constraints introduce less noise in this framework. This property enables censored NHG to achieve a fit comparable to MaxEnt with the original constraint set, but that is only in conjunction with redundant constraints that make it possible to use constraint weights purely to adjust noise. If that redundancy is eliminated by reducing the constraint set, or made irrelevant by augmenting it, then censored NHG performs worse than MaxEnt. Censored NHG only achieves a lower deviance than NHG with the augmented constraint set because censoring results in more uniform standard deviations for the noise difference (σd) across conditions, thus better approximating the fixed standard deviation of MaxEnt, but censored NHG requires an additional constraint weight, so the two models are similar with respect to AIC (ΔAIC = 0.2).
So (i) MaxEnt’s prediction that a given change in constraint violations should always result in the same change in candidate probabilities when those probabilities are measured on the appropriate scale is supported over the NHG’s prediction that changes should depend on the number of violation differences between the candidates. (ii) Measuring probability changes on the logit scale (MaxEnt) seems to yield better results than using the probit scale (normal MaxEnt), but the difference is minimal with the augmented constraint set.
Before concluding, we will briefly address the extension of the analysis of stochastic Harmonic Grammars to cases where three or more variant forms have probabilities significantly above zero.
9. Calculating candidate probabilities with more than two candidates
As noted in section 5, the analysis of the relationship between candidate harmonies and their probabilities developed so far only applies to the analysis of tableaux where two candidates have probabilities significantly above zero, as in the French schwa data. In this section we show how the analysis can be generalized to tableaux with any number of variants and briefly consider further predictions that arise.
The analysis in section 5 considered the case of competition between two candidates, a and b, where the probability that a is preferred over b is the probability that ha + εa > hb + εb, which can be rearranged as in (6), repeated here as (42)
- (42)
For candidate a to be optimal it must have higher harmony than all other candidates, so the probability of selecting candidate a is the probability that, for each candidate b other than a, the random variable εb – εa is less than the difference in harmony scores between the candidates ha – hb. In MaxEnt, where the εi variables follow a Gumbel distribution, it can be shown that this probability is given by the familiar expression in (43) (e.g. Train 2009: 74f.).
- (43)
- Candidate probability in MaxEnt

It is apparent from (43) that it remains true in the general case that the relative probabilities of two candidates depends only on the difference in their harmonies (44).
- (44)
- Ratio of probabilities of two candidates in MaxEnt
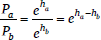
If the εi variables follow a normal distribution, as in normal MaxEnt or NHG, there is no simple closed form expression for Pa, but we can calculate it from the joint distribution of the εb – εa variables, which is a multivariate normal distribution.
For example, consider tableau (1), repeated here as (45). In normal MaxEnt, where the noise added to the harmony of each candidate is drawn from identical normal distributions. Candidate (a) is selected if its harmony is higher than the harmonies of candidates (b) and (c), which is the case if εb – εa is less than ha – hb, which is 1, and εc – εa is less than ha – hc, which is also 1. The joint distribution of εb – εa and εc – εa is the bivariate normal distribution illustrated in Figure 9(a). The variables εb – εa and εc – εa are positively correlated because they both contain -εa, so if εa is high, both are likely to be low, and if εa is low, both are likely to be high. Accordingly the equiprobability contours of the distribution form ellipses with their longer axis running from bottom left to top right. The probability of candidate (a) winning is then the probability that both variables are less than 1, which corresponds to the proportion of the distribution that is shaded in Figure 9(a). This can be calculated by numerical integration methods (Genz & Bretz 2009). If the variance of the εi variables is 1, the probability comes out to 0.634.
The calculation for candidate (b) is represented in Figure 9(b). In this case the random variables are εa – εb and εc – εb, and for candidate (b) to win, these variables must be less than hb – ha = –1 and hb – hc = 0 respectively, which corresponds to the shaded area in the figure. The probability represented by this area is 0.183.
- (45)
- Tableau with probabilities assigned by Normal MaxEnt and NHG
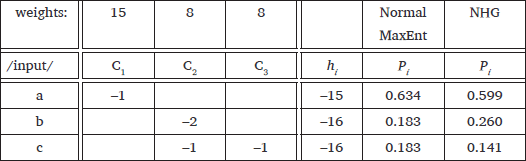
In general, given a tableau with N candidates, the problem of calculating the probability of candidate a reduces to the problem of calculating the probability of N – 1 noise difference variables simultaneously falling below the harmony difference from each other candidate, ha – hb (where b ≠ a). There are algorithms for calculating this probability if the random variables follow a multivariate normal distribution with a known covariance matrix (e.g. Genz & Bretz 2009; Genz 2020). The covariance matrix specifies the shape of the distribution by specifying the covariance between each pair of random variables. So as long as we can determine the relevant covariance matrix, we can calculate candidate probabilities. It turns out that this is straightforward for both normal MaxEnt and NHG, as shown in detail in the supplementary materials, with accompanying R code.
With three or more variants, the predictions of MaxEnt and its normal variant diverge: In MaxEnt the relative probabilities of a pair of candidates depends only on the difference in their harmonies, as shown above, but in normal MaxEnt, candidate probabilities depend on the harmonies of all candidates in the tableau. For example, in (45), if the only candidates were a and b, then Pa = 0.76, Pb = 0.24, and Pa/Pb = 3.2, but with candidate c included, Pa/Pb increases to 3.5 because competition from candidate c reduces the probability of the candidate with lower harmony, i.e. candidate b, more than the candidate with higher harmony, a (cf. Paetz & Steiner 2018).
NHG is still distinguished from both varieties of MaxEnt by the fact that candidate probabilities depend on the pattern of violations across the whole tableau, not just on the harmony differences between candidates. As we have already seen, the variance of the noise difference between a pair of candidates is equal to the sum of the squared violation differences between the two candidates (14), so in (45) the variance of εa – εb is –12 + 22 = 5, whereas the variance of εc – εb is 12 + (–1)2 = 2. The covariance between two noise differences, like εa – εb and εc – εb, is equal to the sum of the products of the violation differences for the two pairs of candidates, i.e. –1 × 0 + 2 × 1 + 0 × –1 = 2 (see appendix for details). So the covariance matrix described above depends on violation differences across the whole tableau. As a result the covariance matrix can be different for each candidate in a tableau, unlike in normal MaxEnt. That is why two candidates with the same harmony scores can have different probabilities in NHG, as illustrated by candidates (b) and (c) in (45).
Censored NHG has to be analyzed by simulation regardless of the number of candidates, but its predictions remain qualitatively similar to NHG, modulated by the effect of constraint weights on noise variances and covariances.
10. Conclusion
We have analyzed stochastic Harmonic Grammars by reformulating them as Random Utility Models, in which Harmonic Grammar is made stochastic by adding random noise to the harmonies of each candidate. In this formulation, the differences between varieties of stochastic Harmonic Grammar follow from differences in the nature of this added noise. More precisely, it is the distribution of differences between these noise terms that is crucial because the relative probabilities of two candidates depends on the difference in their harmonies divided by the standard deviation of the difference between their noise variables, so the probability of reversing a given difference in harmony between two candidates increases as the variance of the noise added to the candidate harmonies increases (Section 5).
The varieties of stochastic Harmonic Grammar that we have considered differ in the shape of the distribution of noise differences and whether the variance of the distribution is fixed or depends on the pattern of constraint violations. In MaxEnt noise differences follow a logistic distribution, while they follow a normal distribution in NHG and normal MaxEnt, and a sum of censored normal distributions in censored NHG. The shape of the distribution determines the precise function that relates the difference in harmonies of two candidates to their probabilities. However, the logistic and normal distributions are similar, so the effects of this difference are generally subtle, although it can result in measurably distinct predictions as probabilities approach 0 or 1, as seen in Section 8.
The more important difference between these models concerns the variance of the noise differences: In MaxEnt and normal MaxEnt, the noise added to each candidate’s harmony has the same variance, so the noise difference also has the same variance for any pair of candidates. In NHG and censored NHG, the variance of the noise difference depends on the number of violation differences for that pair of candidates, so it differs between pairs. Given that candidate probabilities depend on the difference in their harmonies divided by the standard deviation of the noise difference, the fixed variance of the noise difference in both varieties of MaxEnt means that the relative probabilities of candidates depend only on the differences in their harmonies in these frameworks. Where variance of the noise difference depends on violation differences, as in both varieties of NHG, candidate probabilities also depend on the differences in constraint violations between the candidates.
This basic distinction between the grammar models leads to testable predictions concerning the effects of changing constraint violations: In MaxEnt, a given change in constraint violations always has the same effect on the logit of candidate probabilities, whereas in NHG, the effect on candidate probabilities depends on the violation pattern in the whole tableau. In all frameworks, a given change in constraint violations always has the same effect on the harmony difference between candidates. Given fixed variance of noise differences, as in MaxEnt, this means the change in probabilities is also always the same (when measured in logits), but in NHG, the variance of the noise difference can change when constraint violations are changed, so the effect on candidate probabilities depends on the differences in constraint violations between the candidates.
We tested these predictions against Smith & Pater’s (2020) data on schwa realization in French, and the results support MaxEnt over NHG. The MaxEnt grammar provided a much better fit to these data than NHG because the effects on candidate probabilities did not vary in the ways predicted by NHG. Instead, the effect on logit(Pə) of changing constraint violations was generally uniform, as predicted by MaxEnt.
Censored NHG was more competitive with MaxEnt, but that is because in censored NHG noise variance is lower on candidates that violate lower-weighted constraints. This makes it possible to use the weights of redundant constraints to adjust noise variances to better fit the data. However this is not an advantage of the censored NHG framework because the redundancy of constraints here is an artifact of the limited data set being studied. In the absence of the effects of redundant constraints, censored NHG performed worse than MaxEnt, and comparably to regular NHG.
However, evidence from a single data set is obviously not decisive concerning the relative merits of these stochastic Harmonic Grammar frameworks, so the value of this study lies as much in the methods developed here for comparing and evaluating stochastic Harmonic Grammars that can be applied in further studies.
Additional file
The additional file for this article can be found as follows:
Calculating candidate probabilities in stochastic HGs with normal noise. DOI: https://doi.org/10.16995/glossa.5775.s1
R code for working with stochastic HGs and reproducing analyses in the paper. DOI: https://doi.org/10.16995/glossa.5775.s2
Abbreviations
HG = Harmonic Grammar, MaxEnt = Maximum Entropy Grammar, ML = Maximum Likelihood, NHG = Noisy Harmonic Grammar, OT = Optimality Theory
Notes
- This is a somewhat misleading label, since the Maximum Entropy principle that gives Maxent grammar its name actually yields the logistic model. A more appropriate label for the normal variant might be ‘HG with normal candidate noise’, but ‘normal Maxent’ is shorter and makes explicit the similarity to Maxent grammar. [^]
- R code for analyses reported in this paper is included in the supplementary materials. [^]
- Smith & Pater’s censored NHG grammar has deviance 27.2 compared to 12.8 for the grammar reported here. The grammar reported here also performs better on the metrics employed by Smith & Pater: summed absolute errors 0.247 vs. 0.295, summed squared errors 0.010 vs. 0.015. [^]
- Smith & Pater use an underlying normal distribution with standard deviation of 0.2 for censored NHG, resulting in lower constraint weights. [^]
- Deviance is –2 times the difference in Log-likelihood between the model and a ‘saturated’ model with one parameter for each observation (Agresti 2007: 85). [^]
- Thanks to Benjamin Storme for bringing this work to my attention and suggesting that the difference in syntactic structure might be relevant here. Côté (2000) argues that the requirement that consonants be adjacent to a vowel is stronger for consonants adjacent to smaller prosodic boundaries (pp.129ff.). It is not straightforward to employ this form of constraint here because it specifically targets the medial consonant in a CCC cluster, and that consonant is phrase-final in the items with lexical words ([vɛst]AP[ʒon]), but phrase-initial in clitic items ([mɔʁiz]iP[t si'tɛ]). [^]
Acknowledgements
Thanks to Joe Pater for suggesting that data he had collected with Brian Smith might be a good testing ground for MaxEnt and NHG, to an audience at AMP 2017 at NYU for feedback on the early stages of this project, and to two anonymous reviewers for helpful comments on this paper.
Competing Interests
The author has no competing interests to declare.
References
Agresti, Alan. 2007. An Introduction to Categorical Data Analysis, Second Edition. Hoboken: Wiley. DOI: http://doi.org/10.1002/0470114754
Boersma, Paul & Pater, Joe. 2016. Convergence properties of a gradual learning algorithm for Harmonic Grammar. In McCarthy, John J. & Pater, Joe (eds.), Harmonic Grammar and Harmonic Serialism. Sheffield: Equinox.
Burnham, Kenneth P. & Anderson, David R. 2002. Model selection and multimodel inference: a practical information-theoretic approach. New York: Springer. DOI: http://doi.org/10.1007/b97636
Côté, Marie-Hélène. 2000. Consonant cluster phonotactics: A perceptual approach. MIT dissertation. DOI: http://doi.org/10.7282/T3HD7TGR
Dell, François. 1977. Paramètres syntaxiques et phonologiques qui favorisent l’épenthèse de schwa en français moderne. In Rohrer, Christian (ed.) Actes du colloque franco-allemand de linguistique théorique, 141–153. Tübingen: Niemeyer. DOI: http://doi.org/10.1515/9783111681351-008
D’Imperio, Mariapaola & Michelas, Amandine. 2014. Pitch scaling and the internal structuring of the intonation phrase in French. Phonology 31(1). 95–122. DOI: http://doi.org/10.1017/S0952675714000049
Genz, Alan & Bretz, Frank. 2009. Computation of Multivariate Normal and t Probabilities. Lecture Notes in Statistics. Heidelberg: Springer-Verlag. DOI: http://doi.org/10.1007/978-3-642-01689-9
Genz, Alan, & Bretz, Frank & Miwa, Tetsuhisa & Mi, Xuefei & Leisch, Friedrich & Scheipl, Fabian & Hothorn, Torsten. 2020. mvtnorm: Multivariate Normal and t Distributions. R package version 1.1-1. https://CRAN.R-project.org/package=mvtnorm.
Goldwater, Sharon & Johnson, Mark. 2003. Learning OT constraint rankings using a maximum entropy model. In Spenader, Jennifer & Eriksson, Anders & Dahl, Östen (eds.) Proceedings of the Stockholm Workshop on Variation within Optimality Theory, 111–120. Stockholm: Stockholm University, Department of Linguistics.
Hayes, Bruce. 2017. Varieties of Noisy Harmonic Grammar. In Jesney, Karen & O’Hara, Charlie & Smith, Caitlin & Walker, Rachel (eds.), Proceedings of the 2016 Annual Meeting on Phonology. Washington, DC: Linguistic Society of America. DOI: http://doi.org/10.3765/amp.v4i0.3997
Hayes, Bruce. 2020. Deriving the Wug-shaped curve: A criterion for assessing formal theories of linguistic variation. Ms. Los Angeles: UCLA.
Hayes, Bruce & Wilson, Colin. 2008. A maximum entropy model of phonotactics and phonotactic learning. Linguistic Inquiry 39(3). 379–440. DOI: http://doi.org/10.1162/ling.2008.39.3.379
Jesney, Karen. 2007. The locus of variation in weighted constraint grammars. Poster presented at the Workshop on Variation, Gradience and Frequency in Phonology, Stanford University.
Labov, William. 1969. Contraction, deletion and inherent variability of the English copula. Language 45. 715–762. DOI: http://doi.org/10.2307/412333
Michelas, Amandine & D’Imperio, Mariapaola. 2015. Prosodic boundary strength guides syntactic parsing of French utterances, Laboratory Phonology 6(1). 119–146. DOI: http://doi.org/10.1515/lp-2015-0003
Myung, In Jae. 2003. Tutorial on maximum likelihood estimation. Journal of Mathematical Psychology 47. 90–100. DOI: http://doi.org/10.1016/S0022-2496(02)00028-7
Paetz, Friederike & Steiner, Winfried J. 2018. Utility independence versus IIA property in independent probit models. Journal of Choice Modeling 26. 41–47. DOI: http://doi.org/10.1016/j.jocm.2017.06.001
Prince, Alan & Smolensky, Paul. 2004. Optimality Theory: Constraint Interaction in Generative Grammar. Malden: Blackwell. DOI: http://doi.org/10.1002/9780470759400
R Core Team. 2020. A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. URL: https://www.R-project.org/.
Racine, Isabelle. 2008. Les effets de l’effacement du schwa sur la production et la perception de la parole en français. Geneva: University of Geneva dissertation. DOI: http://doi.org/10.13097/archive-ouverte/unige:602
Smith, Brian W., & Pater, Joe. 2020. French schwa and gradient cumulativity. Glossa: A Journal of General Linguistics 5(1). 24.1–33. DOI: http://doi.org/10.5334/gjgl.583
Smolensky, Paul & Legendre, Geraldine. 2006. The harmonic mind: From neural computation to optimality theoretic grammar. Cambridge: MIT Press.
Train, Kenneth E. 2009. Discrete Choice Methods with Simulation, 2nd Edition. Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/CBO9780511805271
Zuraw, Kie & Hayes, Bruce. 2017. Intersecting constraint families: an argument for Harmonic Grammar. Language 93(3). 497–548. DOI: http://doi.org/10.1353/lan.2017.0035