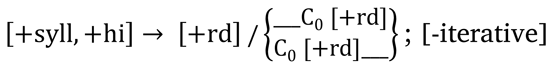1 Introduction

In many cases, feature spreading is iterative, applying to all licit targets within a given domain. In serial, rule-based formalisms, accounting for iterative rule application requires special formal and notational devices, like parenthesis-star notation, assigning rules a [±iterative] feature, or stipulating the direction of evaluation (Chomsky & Halle 1968; Howard 1973; Jensen & Stong-Jensen 1973; Anderson 1974; Kenstowicz & Kisseberth 1977: ch.5). The addition of these parameters, to varying degrees, assigns an ontological status to both iterativity and non-iterativity. On the other hand, as discussed in Kisseberth (2007) and Kaplan (2008), iterativity and non-iterativity are regarded quite differently in Optimality Theory (OT; Prince & Smolensky 2004). In OT, iterativity and non-iterativity fall out indirectly from global optimization over interacting constraints. For instance, an Agree constraint (Lombardi 1999; Baković 2000) delimiting the syntagmatic realization of [F] within some phonological domain, in conjunction with some set of relatively vanilla constraints will result in iterative agreement for [F] throughout the entire domain. Thus, iterativity falls out indirectly from constraint interaction in OT, while in derivational frameworks the analysis of iterativity demands additional stipulations.

Though this might seem to be a feather in OT’s cap, analyzing non-iterative patterns reveals a more complex formal situation. With some formal device like a [±iterative] rule feature, a derivational account has no trouble with non-iterative spreading since both iterative and non-iterative patterns are given a relatively clear status in the theory. However, non-iterativity is a more challenging issue for OT. Discussing Yip’s (2002) analysis of local tone shift, a pattern where a high tone appears to relocate to the next tone-bearing unit, Kisseberth (2007) notes the central issue for OT – the structure of basic markedness and faithfulness constraints is largely incapable of formalizing non-iterative patterns. Yip’s Local constraint, defined as “spread only to the adjacent element” (2002:84), is, in practice, untenable. Yip’s constraint needs to determine both the underlying location of the high tone as well as the extent of spreading on the surface. Since markedness constraints evaluate surface structures only, and faithfulness constraints typically evaluate input-output pairs, the analysis of non-iterative patterns is not clear-cut in OT.

Kaplan (2008) responds to Kisseberth’s critique by arguing that non-iterativity is always epiphenomenal, being derivable from independent forces in a given language. Concerning OT, Kaplan writes, “[w]hen a process applies (non)iteratively, it does so because that happens to be the best way to satisfy some output desideratum, not because the process is specifically required to be (non)iterative” (2008:2). Thus, although iterativity may be derivable from a simple set of OT constraints, neither iterativity nor non-iterativity possess any real formal status in the theory. Each is the byproduct of other, independent structural features of the language in question. To support this claim, Kaplan (2008) devotes much time to demonstrating that attested cases of apparently non-iterative feature spreading are actually byproducts of other factors, some phonetic, some phonological.

This paper examines the status of non-iterativity with data from Crimean Tatar (Sevortjan 1966; Kavitskaya 2010). In the Southern dialect, [+round] spreads from an underlying round vowel to all following [+high] vowels. However, in the Central dialect, [+round] spreads only once, leaving all subsequent vowels to surface faithfully. If Kaplan’s claim is correct, then the extent of harmony in the Southern dialect is not really due to iterativity. Likewise, under his analysis, the extent of harmony in the Central dialect does not derive from any direct reference to non-iterativity, but rather something else. Using a production study, we examine both the empirical facts of harmony in these two dialects, as well as the formal status of non-iterativity. To preview our results, we find some acoustic evidence to support a qualitative difference between the extent of rounding harmony in the Southern and Central dialects of the language. Production results are supplemented with new data demonstrating non-iterativity among harmony-triggering suffixes. These data further support our claim that the extent of rounding harmony in Central Crimean Tatar is truly non-iterative.

The paper is structured as follows. In Section 2, we discuss the issue of iterativity in phonological theory. In Section 3, we describe the basic harmony pattern in Crimean Tatar, and in Section 4 we present results from a production study to determine at a more basic level how far rounding extends in the word. Section 5 presents crucial data from suffixal triggers, and Section 6 evaluates the case for non-iterative spreading in Central Crimean Tatar. Section 7 discusses the formal analysis of non-iterative patterns in rule- and constraint-based theories, and Section 8 briefly describes several other non-iterative spreading patterns. In Section 9 we conclude the paper.

2 Iterativity and non-iterativity

From the advent of the Generative program, phonologists have wrestled with how a rule applies to an input. In Chomsky & Halle (1968:344), rule application is simultaneous, meaning that when the structural description of some rule is met, that rule applies simultaneously to all licit targets. As a consequence, no rule can feed or bleed itself, and Chomsky & Halle introduce parenthesis-star notation to generate patterns of unbounded feature spreading. Howard (1973) and Anderson (1974) discuss cases of self-feeding and self-bleeding rules, arguing for iterativity and directionality as necessary primitives within a serial, rule-based formalism (see also Kenstowicz & Kisseberth 1977: ch.5). Although some later work, e.g., Archangeli & Pulleyblank (1994) and Nevins (2010) adopt similar parametric theories of rule application, more recent discussion of iterativity is limited.

The most far-reaching theory of iterativity and non-iterativity in recent work comes from Kaplan (2008). As indicated above, Kaplan (2008) contends that all semblances of iterativity and non-iterativity are emergent, and thus not formally real. He calls his claim the Emergent non-iterativity hypothesis, in (1).

    1. (1)
    1. Emergent non-iterativity hypothesis: No formal entity in phonological grammars may require non-iterativity (Kaplan 2008:2).

Kaplan goes on to exemplify his claim by discussing a number of putatively non-iterative patterns. Specifically, he argues that the domain of spreading in the relevant cases falls out from word-internal domains, non-intersection of potential triggers and targets, prominence-targeting spreading, or phonetic implementation. These four types of emergent non-iterativity are discussed and exemplified below. We will contrast these four types of emergent non-iterativity with the true non-iterativity exemplified in Central Crimean Tatar in later sections.

2.1 Word-internal domains

Perhaps the simplest form of emergent non-iterativity is due to sub-word domains. If some spreading pattern operates within a given domain, and that domain ranges over two syllables only, then the extent of harmony can be derived from the size of the domain without reference to non-iterativity. The most well-known two-syllable domain is the metrical foot, and Pearce (2006; 2007) argues that the extent of fronting harmony in Kera is definable precisely in metrical terms. Kera builds iambic feet from left to right, and allows the following foot types: (CV.CVː), (CV.CVC), (CVː), (VC), and (CVC). In disyllabic feet, the head controls the frontness of the preceding non-head (2). When the imperfective suffix attaches to a root with a back vowel it triggers fronting of the root if the two can be syllabified into a single foot (2a–c). In cases where the two are not footed together, the underlying backness of the root vowel is maintained (2d–f).1

    1. (2)
    1. Foot-bounded frontness spreading in Kera
    1. a.
    2. b.
    3. c.
    4. d.
    5. e.
    6. f.
    1. /bàl-ɛ́/
    2. /bɨ̀ŋ-ɛ́/
    3. /ɨ̄s-ɛ́/
    4. /bàːd-ɛ́/
    5. /vɨ̀ːɡ-ɛ́
    6. /ɨ̄sk-ɛ́/
    1. (bè.lɛ̀ː)
    2. (bì.ŋìː)
    3. (í.síː)
    4. (bàː)dɛ̀
    5. (vɨ̀ː)ɡì
    6. (ɨ́s)kí
    1.  
    2.  
    3.  
    4. *(bèː)dɛ̀
    5. *(vìː)ɡi
    6. *(ís)kí
    1. ‘love-impf’
    2. ‘open-impf’
    3. ‘sit.down-impf’
    4. ‘wash-impf’
    5. ‘empty-impf’
    6. ‘hear-impf’

Regressive frontness harmony in Kera is thus foot-bounded, which is supported by a range of other data marshalled in Pearce (2006; 2007). A number of other languages have metrical systems that can be leveraged to account for the extent of feature spreading (cf. Piggott’s (1996) ‘harmony foot’). For instance, frontness harmony in Veps applies to the second-syllable only, which aligns with the right edge of the word-initial trochee in the language (Zaiceva 1981). Additionally, Wang & Lin (2017) propose that the foot delimits the domain of tone sandhi in Tianjin Chinese.

2.2 Non-intersection of triggers and targets

In some cases, the extent of feature spreading is defined by the featural makeup of triggers and targets. Specifically, if the set of triggers does not intersect with the set of outputs then the pattern cannot possibly feed itself. Consider the case of Bengali in (3). ATR harmony in the language operates from right to left, and is triggered by [+high] vowels only. Harmony targets mid vowels, triggering assimilation of /ɛ ɔ/ to [e o]. However, since the outputs of harmony are mid and not high, they cannot further propagate [+ATR] spreading.

    1. (3)
    1. Trigger-target non-intersection in Bengali (Mahanta 2008:152–153)
    1.  
    2. a.
    3. b.
    4. c.
    1. Unsuffixed
    2. pɔtʰ
    3. pɔd
    4. ɔʃɔt
    1. Gloss
    2. way
    3. position
    4. dishonest
    1. Suffixed
    2. potʰik
    3. pɔdobi
    4. ɔʃoti
    1. Gloss
    2. traveler
    3. position.holder
    4. dishonest.f

Similar patterns are found in Mayak (Andersen 1999), Icelandic (Anderson 1974; Jurgec 2011), and Sanskrit (Whitney 1879; Allen 1951; Ryan 2017). In patterns like these, iterativity is simply precluded by the conditions on triggers and targets (Jurgec 2011; Chandlee 2021).

2.3 Prominence-targeting spreading

In many instances, feature spreading is initiated by some prominent position in the word, like a morphological root, a stressed syllable, or a word edge. However, Walker (2005; 2011) and Kaplan (2008; 2015) suggest that some spreading patterns involve weak triggers. In these cases, spreading is initiated by a weak element and targets a strong element.

In the Romance dialect of Grado, some word-final high vowels trigger raising of some preceding vowels (Walker 2005). In (4a–c), word-final high vowels target a single preceding mid vowel, raising it to high. In (4d), though, the word-final high vowel assimilates two preceding mid vowels to high. Note that the difference in these is definable in terms of stress and not syllable number. Metaphonic raising extends leftward to the stressed syllable, and thus may extend to one or sometimes two syllables in order to reach its target.

    1. (4)
    1. Stress-targeting metaphony in Grado (Walker 2005: 924–925)
    1.  
    1. Post-tonic vowel is [–high]
    1. Post-tonic vowel is [+high]
    1.  
    1. a.
    2. b.
    3. c.
    4. d.
    1. mét-o
    2. rénd-e
    3. odorós-o
    4. ʃóven-e
    1. put-1.sg
    2. return-3.sg
    3. odorous-m.sg
    4. young.man-m.sg
    1. mít-i
    2. rínd-i
    3. odorús-i
    4. ʃúvin-i
    1. put-2.sg
    2. return-2.sg
    3. odorous-m.pl
    4. young.man-m.pl

Walker’s (2005) analysis requires that the [+high] feature be affiliated with a strong position, and in order to satisfy the licensing requirement, the language spreads [+high] to overwrite the height feature of the stressed syllable (see also Kaplan 2015).

Kaplan (2008) argues that this same sort of licensing is found in ATR harmony in Lango, where suffix-initiated ATR harmony terminates after assimilating a single root vowel due to a constraint demanding that ATR be affiliated with the root. While iterative spreading throughout the root would also satisfy this requirement, doing so would incur gratuitous violations of faithfulness.

2.4 Phonetic implementation

Thus far, discussion has centered primarily on segmental patterns. Bantu tonal patterns typically involve spreading or shifting. Spreading is usually rightward, and may either extend to one adjacent syllable, or throughout a larger word or phrasal domain. Tone shifting on the other hand involves the displacement of an underlying tone, typically one syllable to the right (see Kisseberth & Odden 2003; Hyman 2011 for overviews).

An interesting case of tone shifting comes from Kikuyu (Clements 1984). In (5a,b), observe that all morphemes are underlyingly toneless (or alternatively, low toned). However, in (5c) the object prefix /má-/ is underlyingly high toned, but that tone surfaces on the following vowel in the underlyingly toneless root /rɔr/. In (5d), the underlyingly high-toned root /tóm/ surfaces with its high tone one syllable to the right, on the toneless suffix /-aɣ/. Finally, in (5e), both the object prefix and the root bear high tones, and both of these shift one syllable to the right.2

    1. (5)
    1. Tone shifting in Kikuyu
    1. a.
    2. b.
    3. c.
    4. d.
    5. e.
    1. /to-rɔr-aɣ-a/
    2. /to-mo-rɔr-aɣ-a/
    3. /to-má-rɔr-aɣ-a/
    4. /to-tóm-aɣ-a/
    5. /to-má-tóm-aɣ-a/
    1. [to-rɔr-aɣ-a]
    2. [to-mo-rɔr-aɣ-a]
    3. [to-ma-rɔ́r-aɣ-a]
    4. [to-tom-áɣ-a]
    5. [to-ma-tóm-áɣ-a]
    1. “we look at”
    2. “we look at him/her”
    3. “we look at them”
    4. “we send”
    5. “we send them”

In cases like this, there is no obvious domain or target that determines the nature of the shift. High tones from roots or prefixes undergo shifting in (5). Further, there is no obvious target for shifting, since shifting may result in a high-toned root or suffix. Kaplan’s analysis builds on insights from Myers (1999; 2003), which reports that high tones may be realized late within their target syllable or even in the following syllable, a phenomenon called peak delay. If the realization of a high tone requires more time than other tones, then non-iterative rightward tone shift, as well as tone spreading, is very plausibly a phonetic fact. Peak delay has been used to account for tonal patterns in Chichewa, Kinyarwanda, as well as Mandarin (Myers 1999; 2003; Xu 2001). If non-iterativity in tonal processes is phonetic in nature, understood as the gestural lag necessary to realize a high tone, then these relatively common tonal processes are not truly challenges to Kaplan’s hypothesis (cf. Key & Bickmore 2014).

2.5 Summary of types of epiphenomenal non-iterativity

In the preceding subsections we outlined four types of patterns that result in apparent non-iterativity. In all of these, Kaplan contends that non-iterativity is not formally necessary since independent phonological, morphological, or phonetic factors determine the extent of spreading. In the first type, a word-internal domain (e.g., the foot) delimits the extent of spreading. In the second type, spreading appears to be non-iterative only because the set of triggers and potential targets do not share the relevant features. In the third type, feature spreading derives from weak triggers targeting strong positions to satisfy a licensing requirement. Fourth, apparent non-iterative spreading may also be due to the phonetic implementation of the phonological feature in question. When the phonetic realization of the phonological feature requires a relatively large amount of time, e.g., high tone, this may result in apparent non-iterativity.

These facts provide a framework through which to view reported patterns of non-iterativity in order to determine whether the extent of spreading is formally derivable from independent facts about the language, or if iterativity and non-iterativity are more fundamental parts of the phonological grammar. We will see that the rounding harmony pattern in Central Crimean Tatar does not conform to any of Kaplan’s proposed categories, presenting the clearest evidence to-date that non-iterative feature spreading is not always a byproduct of other factors in the language.

3 Crimean Tatar

3.1 The general pattern

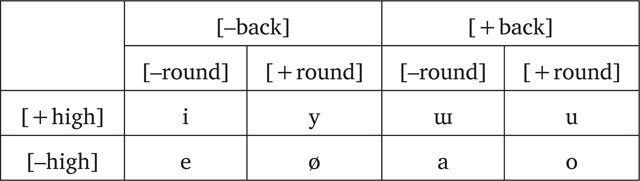
Crimean Tatar (iso: crh) is a Turkic language spoken primarily on the Crimean Peninsula, and by diaspora speakers in Central Asia, Turkey, Eastern Europe, and North America. Southern Crimean Tatar has an inventory of eight contrastive vowels, /i y e ø a o ɯ u/, while the Central and Northern dialects possess an additional vowel /ɨ/ (Berta 1998; Kavitskaya 2010; 2013). The eight vowels that are common to all three dialects are describable in terms of three binary oppositions [±back], [±round], and [±high], in (6).

    1. (6)
    1. Crimean Tatar vowel features

In all three dialects, backness harmony operates extensively. As for rounding harmony, in the Northern dialect rounding harmony is absent, and even initial-syllable /y u/ may be unrounded. Consequently, we focus on the Southern and Central dialects. In the Southern dialect, [+round] spreads rightward, typically from the initial syllable, to all following high vowels. However, in the Central dialect [+round] spreads only once. These two dialects are compared in (7). Since the initial-syllable vowel is [–round] in (7a–d) second-syllable vowels are [–round], too. In (7e–h) though, the same nominalizing and possessive suffixes are rounded to [y] and [u] due to the presence of a round vowel in the initial syllable. In (7i,j), the two dialects diverge, with harmony in the Southern dialect applying to third-syllable vowels, while in the Central dialect harmony applies to second-syllable vowels only, leaving the possessive suffix unassimilated. Note that the third-person possessive suffix alternates for harmony when it immediately follows an underlyingly [+round] vowel (7b,d,f,h). Thus, the incomplete round spreading in the Central dialect in (7i,j) is not due to some morpheme-specific fact about the possessive suffix.

    1. (7)
    1. Rounding harmony in Crimean Tatar
    1.  
    2. a.
    3. b.
    4. c.
    5. e.
    6. f.
    7. g.
    8. h.
    9. i.
    10. j.
    1. Southern
    2. tez-lik
    3. tez-i
    4. qɯz-lɯq
    5. køz-lyk
    6. køz-y
    7. tuz-luq
    8. tuz-u
    9. køz-lyɡ-y
    10. tuz-luɣ-u
    1. Central
    2. tez-lik
    3. tez-i
    4. qɯz-lɯq
    5. køz-lyk
    6. køz-y
    7. tuz-luq
    8. tuz-u
    9. køz-lyɡ-i
    10. tuz-luɣ-ɯ
    1. Gloss
    2. ‘speed-nmlzr’
    3. ‘speed-poss.3’
    4. ‘girl-nmlzr’
    5. ‘eye-nmlzr’
    6. ‘eye-poss.3’
    7. ‘salt-nmlzr’
    8. ‘salt-poss.3’
    9. ‘eye-nmlzr-poss.3’
    10. ‘salt-nmlzr-poss.3’

4 Production study

Recent work has shown that experimental studies are useful follow-ups to impressionistic transcriptions of phonological phenomena. In some cases, experimental results have shown that previous claims were (to varying degrees) incomplete or inaccurate (e.g., Van Zanten, Goedemans & Pacilly 2003; de Lacy 2014; Shih 2018; Bowers 2019). In the domain of suprasegmental patterns, in particular word-level stress, such experimental results have been crucial to recent scholarship because the cues to stress are often subtle, and are difficult for non-native linguists to accurately perceive. Similarly, phonetic examination of harmony patterns has been used to determine whether a particular spreading pattern is phonetic or phonological in nature. As an example, Hess (1992) and Casali (2012) examine the degree of assimilation of certain Akan vowels across word boundaries to determine if phrasal [+ATR] spreading is phonological, or if it only represents a lower-level coarticulatory effect. Like stress and the particular ATR-related effects in Akan, the acoustic effects of lip rounding are relatively subtle (Kaun 1995: ch. 5). Therefore, a production study aimed at determining the extent of phonological rounding, especially when coarticulatory (phonetic) rounding is also present, is a plausible means of evaluating existing descriptions of Crimean Tatar, which allows for a more confident assessment of the theoretical significance of the pattern.

4.1 Methods

4.1.1 Speakers

Through existing relational networks, we recruited four speakers of the Southern dialect (2 females, average age: 59 yrs, age range: 51–67 yrs) and five speakers of the Central dialect (5 females, average age: 64.6 yrs, age range: 60–77 yrs) to participate in the study.

4.1.2 Stimuli

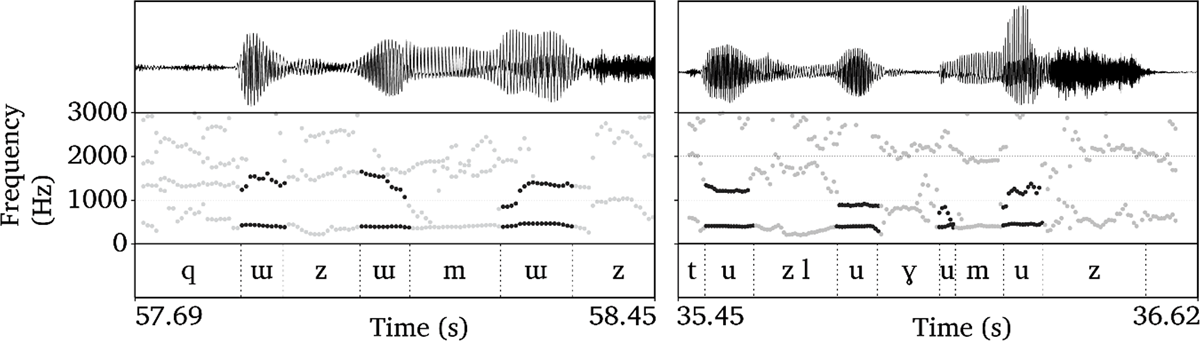
Speakers were presented a wordlist (n=368 words) consisting of minimal and near-minimal pairs for each of the eight shared vowel contrasts in the two dialects. The lexical roots in the wordlist are shown in (8). Both mono- and disyllabic roots were elicited because existing descriptions of the Central dialect (e.g., Kavitskaya 2013) report that disyllabic roots do not spread rounding onto a suffix, e.g., [jyzym-i] ‘grape-poss.3s’. This suggests that the second syllable of such roots is a target of harmony rather than having its own underlying [+round] feature. Speakers produced target words up to four syllables in length. Due to the relative sparsity of measurements from fourth-syllable vowels, the analysis only evaluates data from syllables one to three in the forms shown in (9l–n). See Figure 1 for a spectrogram of a four-syllable word elicited from a speaker of the Southern dialect.

Figure 1
Figure 1

Sample waveforms and formant tracks (black for vowel F1 and F2; gray otherwise) for [qɯz-ɯmɯz] ‘girl-poss.1p’ and [tuz-luɣ-umuz] ‘salt-nmlzr-poss.1p’ produced by Speaker 9 (southern, female, 62 years old).

    1. (8)
    1. Roots elicited
    1.  
    2. a.
    3. b.
    4. c.
    5. d.
    6. e.
    7. f.
    8. g.
    9. h.
    1. Vowel
    2. a
    3. o
    4. e
    5. ø
    6. ɯ
    7. u
    8. i
    9. y
    1. Roots
    2. al ‘take’, tal ‘willow’, qaz ‘goose’, arɯq ‘ditch’
    3. ol ‘be’, qol ‘arm/hand’, soluq ‘breath’, qoʃu ‘horse race’, qoruv ‘security’, qozu ‘lamb’
    4. kel ‘come’, el ‘nation’, kez ‘meet’, teʃik ‘hole’, kerik ‘dilated’
    5. øl ‘die’, køl~ɡøl ‘lake’, øz ‘self’ søz ‘word’, køz~ɡøz ‘eye’
    6. qɯl ‘hair’, qɯz ‘girl’
    7. qul ‘slave’, qur ‘build’, tuz ‘salt’
    8. il ‘hang’, til ‘language’, tiz ‘knee’, is ‘smell’, tiʃ ‘tooth’
    9. kyl ‘laugh’, kyl ‘ash’, ɡyl ‘flower’, kyz ‘autumn’, jyz ‘face’, tyʃ ‘dream’, jyzym ‘grape’, symyk ‘snot’

The wordlist contained a range of suffixes appended to each root. Two example series of inflected forms are shown in (9), one for nominal roots and one for verbal roots. Words were represented in Cyrillic. In the standard orthography, which is based on the Central dialect, rounding harmony is represented on second-syllable high vowels. Words were produced in the carrier sentence in (10).

    1. (9)
    1. Sample inflected forms
    1.  
    2. a.
    3. b.
    4. c.
    5. d.
    6. e.
    7. f.
    8. g.
    9. h.
    10. i.
    11. j.
    12. k.
    13. l.
    14. m.
    15. n.
    1. /tuz/
    2. tuz-um
    3. tuz-uŋ
    4. tuz-u
    5. tuz-umɯz
    6. tuz-uŋɯz
    7. tuz-lar-ɯ
    8. tuz-lu
    9. tuz-suz
    10. tuz-luq
    11. tuz-luɣ-ɯm
    12. tuz-luɣ-ɯ
    13. tuz-luɣ-ɯmɯz
    14. tuz-luɣ-ɯŋɯz
    15. tuz-luq-lar-ɯ
    1. ‘salt’
    2. poss.1s
    3. poss.2s
    4. poss.3
    5. poss.1p
    6. poss.2p
    7. pl.poss.3
    8. adj
    9. priv
    10. nmlzr
    11. nmlzr-poss.1s
    12. nmlzr-poss.3
    13. nmlzr-poss.1p
    14. nmlzr-poss.2p
    15. nmlzr-pl.poss.3
    1.  
    2. o.
    3. p.
    4. q.
    5. r.
    6. s.
    7. t.
    8. u.
    9.  
    10.  
    11.  
    12.  
    13.  
    14.  
    15.  
    1. /qur/
    2. qur-maq
    3. qur-du-m
    4. qur-du-ŋ
    5. qur-du
    6. qur-du-q
    7. qur-du-ŋɯz
    8. qur-du-lar
    9.  
    10.  
    11.  
    12.  
    13.  
    14.  
    15.  
    1. ‘build’
    2. inf
    3. pst-1s
    4. pst-2s
    5. pst.3s
    6. pst-1p
    7. pst-2p
    8. pst.3-pl
    9.  
    10.  
    11.  
    12.  
    13.  
    14.  
    15.  
    1. (10)
    1. Carrier sentence
    2. Тилимизде _____ сёзю бар.
    3. Til-imiz-de _____ søz-y bar
    4. language-poss.1p-loc _____ word-poss.3s exist
    5. “In our language, the word _____ exists.”

4.1.3 Recording and measurements

All sessions were conducted in a quiet room, and audio data were recorded to a Zoom H6 at a sampling rate of 44.1 kHz with a Shure unidirectional microphone. All sound files were segmented in Praat (Boersma & Weenink 2015). The beginning and end of each vowel were aligned to the onset and offset of the second formant. In cases where the second formant persisted across flanking consonants (sonorants), abrupt shifts in the amount and distribution of spectral energy were used to indicate vowel onset and offset. Sample waveforms with formant tracks are shown in Figure 1.

After segmentation, the first three formants (F1, F2, and F3, in Hz) at vowel midpoint were measured, in addition to duration (ms), mean intensity (dB), mean f0 (Hz), maximum intensity (dB), and maximum f0 (Hz). Since formant structure is significantly affected by flanking consonants, we measured formants at vowel midpoint to minimize effects from flanking consonant place of articulation.

Formant values were z-score normalized (Lobanov 1971) to facilitate more meaningful between-speaker comparisons. The data for normalization consisted of eight tokens of each vowel and were taken from monosyllabic words. If eight tokens of a given vowel were not present in monosyllables, then the remaining tokens were taken from the initial syllable of disyllabic words. The data were manually inspected for outliers; 129 data points were removed from the 3,188 tokens recorded from speakers of the Southern dialect, and 113 data points were removed from the 3,122 tokens recorded from speakers of the Central dialect (approximately 4% from each dialect). The majority of these outliers were due to formant tracking errors.

4.1.4 General observations

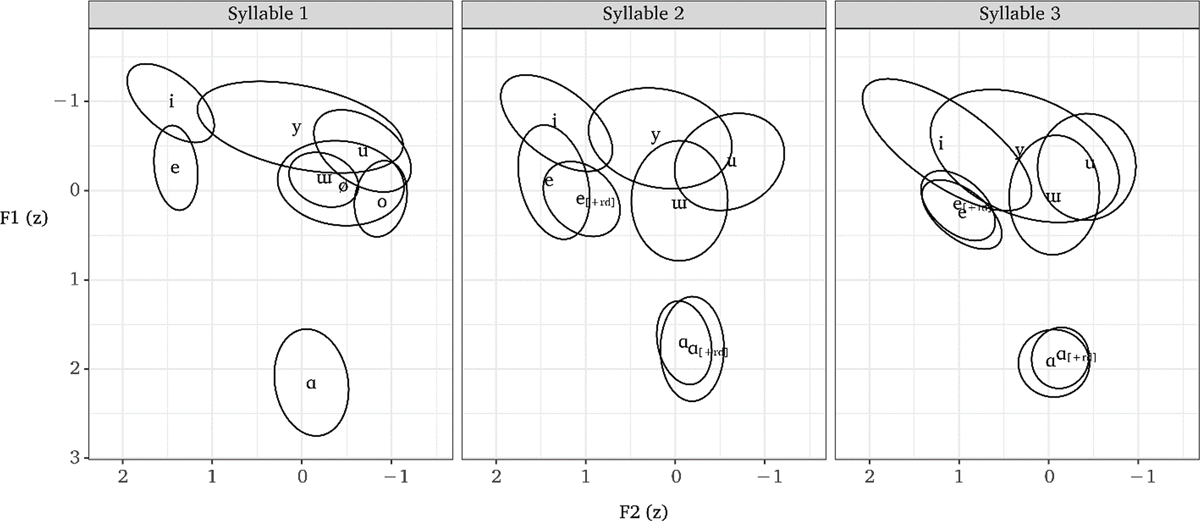
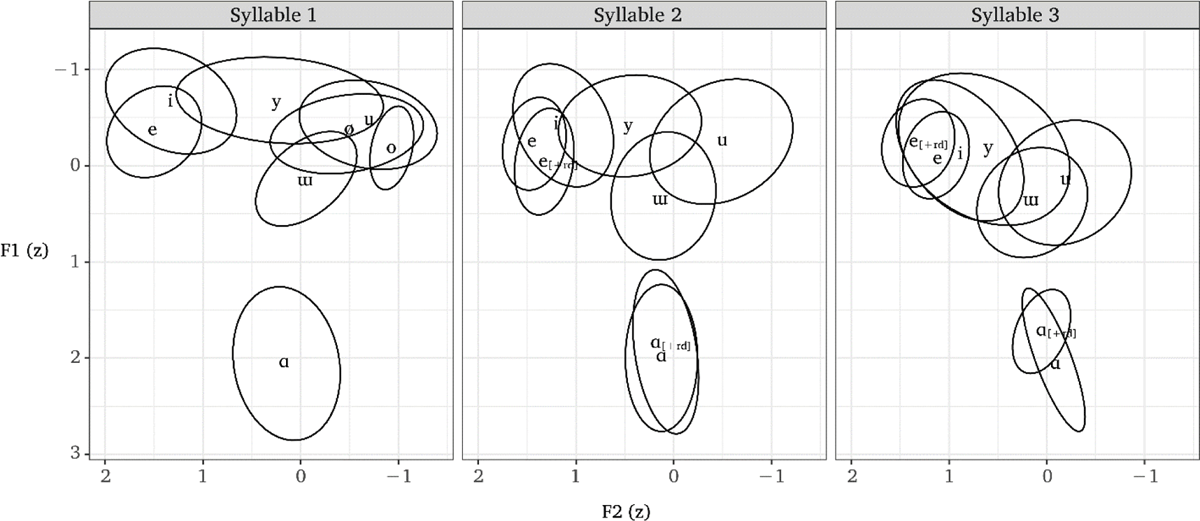
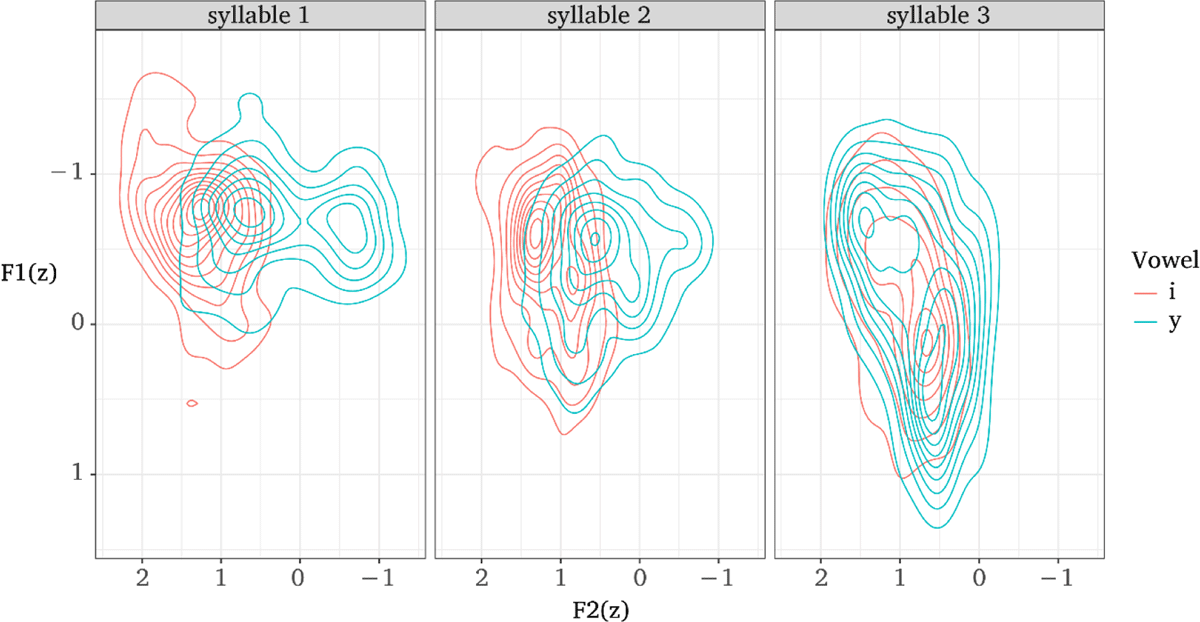
Before proceeding to the results that inform the paper, let us first consider some general properties of the vowel systems in these two dialects. Combined vowel plots for each dialect are presented in Figure 2 and Figure 3. In each figure, vowels are plotted by syllable. Since mid rounded vowels [ø o] do not occur in second or third syllables, the vowel inventory is effectively reduced to six vowels in non-initial syllables. Non-high vowels after [+round] roots are indicated with [+rd] subscripts in Figure 2 and Figure 3, ɑ[+rd] and e[+rd]. The reduction of the inventory in non-initial syllable is evident in the center and rightmost panels of each figure, where the ellipses for /e/-/e/[+rd] and /ɑ/-/ɑ/[+rd] overlap almost entirely, indicating only very minor coarticulatory rounding on non-initial mid and low vowels. Observe also in both dialects that /y/ varies greatly between an acoustically front and back vowel, particularly in initial syllables. Kavitskaya (2010:14–17) reports backing of initial-syllable /y ø/ to [u o] before some consonants in the Central dialect. Throughout our data, the realization of initial-syllable /y ø/ was dependent on preceding consonantal place; phonetically front round vowels were produced after coronals, while phonetically back round vowels were produced elsewhere. We return to this issue below.

Figure 2
Figure 2

By-syllable F1-F2 (z) vowel plots for speakers of the Southern dialect. Non-high vowels that followed [+round] triggers are marked with a [+rd] subscript.

Figure 3
Figure 3

By-syllable F1-F2 (z) vowel plots for speakers of the Central dialect. Non-high vowels that followed [+round] triggers are marked with a [+rd] subscript.

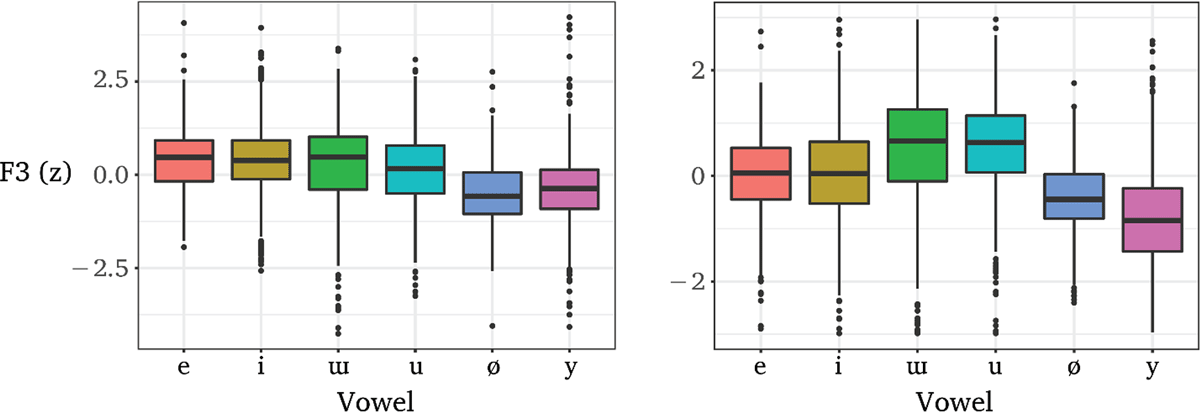
Relative F2 of each vowel is also evident in Figure 4, which shows the distribution of F2 for each vowel quality pooled across all contexts. Unrounded vowels have relatively high F2 while rounded vowels have relatively low F2.

Figure 4
Figure 4

F2(z) for each vowel pooled across all contexts in Central (left panel) and Southern (right panel) Crimean Tatar.

F3 for each vowel is shown in Figure 5. Note that in this figure, the differences in F3 for round and unrounded vowels are small and inconsistent. McCollum (2015) and Lionnet (2017) report that F3 is not a reliable correlate of lip rounding in Kazakh and Laal, and this appears to hold for Crimean Tatar, too. As a result, we consider only the effect of rounding on F2 throughout the rest of the paper.

Figure 5
Figure 5

F3 (z) for each vowel in Central (left panel) and Southern (right panel) Crimean Tatar.

4.1.5 Analysis

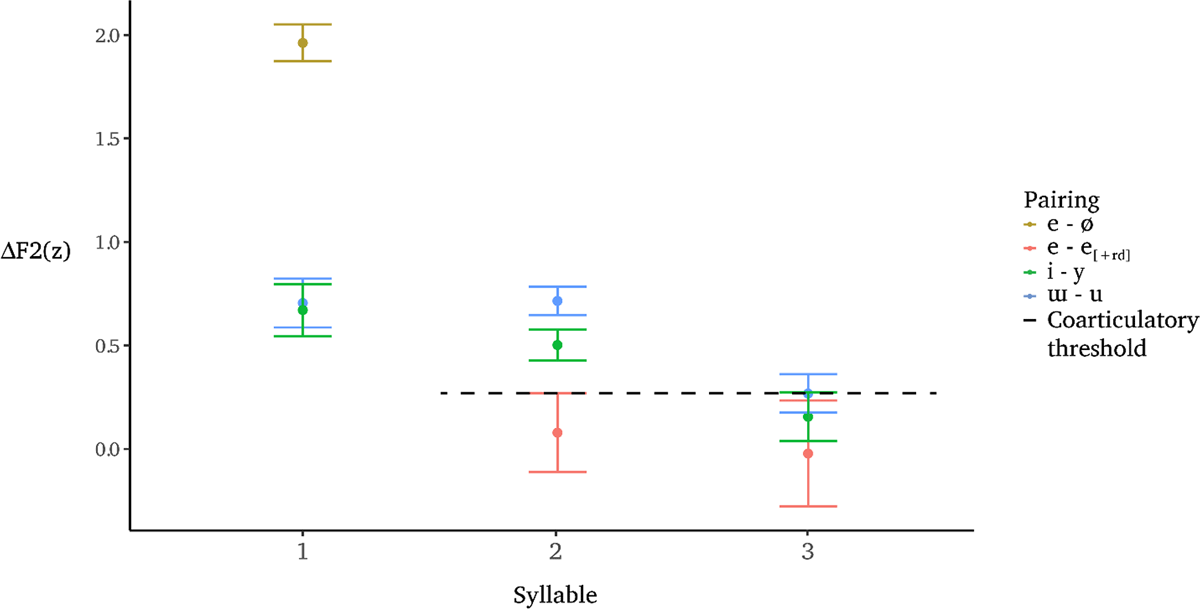
The goal of the statistical analysis was to determine if third-syllable high vowels undergo phonological [+round] spreading or not. Stated differently, we are interested in whether the effect of initial-syllable rounding is phonological or perhaps phonetic in syllable three. In order to determine whether third-syllable effects are phonological or not, an independent threshold for coarticulatory effects is necessary. We operationalized this threshold as the difference in F2 of /e/ after [±round] vowels (e.g., second-syllable [e] in [køl-de] ‘lake-loc’ versus [el-de] ‘nation-loc’). Although using /ɑ/ and /o/ for such a threshold is possible, the difference in both F1 and F2 make determining the coarticulatory effect of rounding less straightforward.

In order to determine the actual coarticulatory threshold, as well as ΔF2 values for the high vowels, we constructed a mixed-effects regression using the lme4 package in R (Bates et al. 2015; R Core Team 2017). We predicted F2(z) based on harmonic pairing, rounding, and syllable number, as well as all possible interactions. The model’s random effect structure included random intercepts for speaker, preceding context, and following context. Context differentiated six different environments (word edge, bilabial, dental, liquid, (alveo-)palatal, and dorsal). The model failed to converge with more elaborate random effect structures. Pairwise comparisons were conducted using the emmeans package (Lenth et al. 2018). The upper confidence limit around the mean of ΔF2/e/ in syllable 2 after round versus unrounded vowels was then used as the null hypothesis for a series of one-tailed one-sample t-tests to determine if ΔF2 for some pairing in some position is greater than the coarticulatory threshold. Our analytical method follows other work in assuming that a categorical effect is likely to result in full neutralization of phonetic contrast, in contrast to a gradient, phonetic effect, which will result in an intermediate vowel quality (e.g., Hess 1992). By operationalizing the magnitude of the assimilation as ΔF2, and embedding this in a mixed-effects model, we attempt to analyze the extent of phonological spreading.

4.2 Predictions

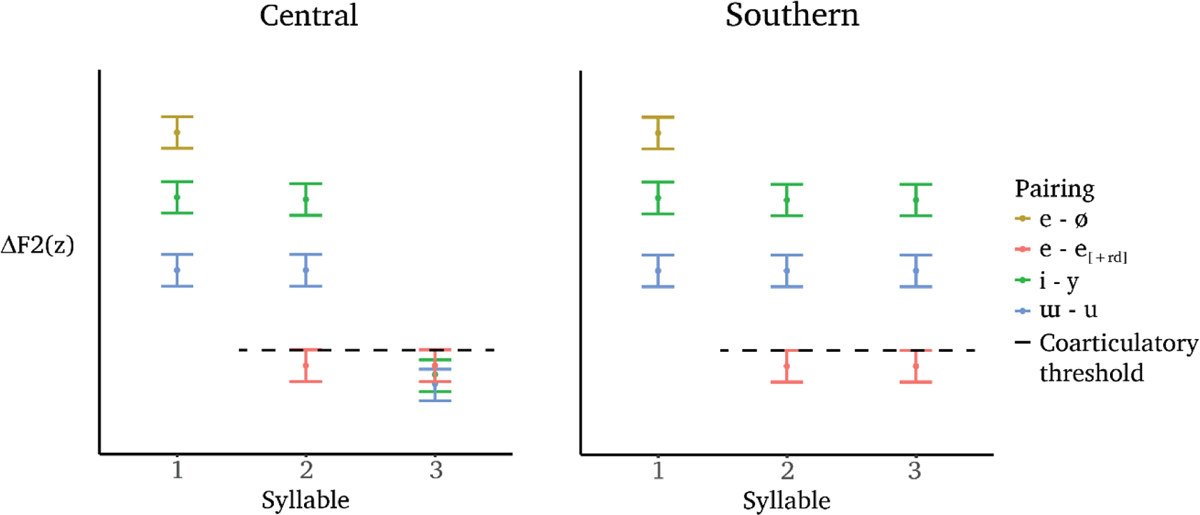
Since [+round] spreading is iterative in the Southern dialect, ΔF2 of second- and third-syllable high vowels should be significantly greater than the coarticulatory threshold (i.e., second-syllable ΔF2 for /e/). In contrast, if harmony is non-iterative in the Central dialect, then only ΔF2 of second-syllable high vowels should exceed the threshold. Consider the two idealized plots of our predictions in Figure 6. In each, ΔF2 of each pairing is plotted for syllables one through three. In each, the realization of /e/ after [±round] vowels (red) serves as the point of comparison for phonological harmony and phonetic coarticulation. If harmony applies, ΔF2 should be greater than the coarticulatory threshold; if harmony does not apply, ΔF2 should not be significantly greater than the threshold.

Figure 6
Figure 6

Idealized ΔF2(z, with 95% confidence intervals) for each vowel pairing and syllable compared to the coarticulatory threshold in Central and Southern Crimean Tatar.

In the Southern dialect, all else being equal, we predict that ΔF2 for both /i-y/ and /ɯ-u/ should be equivalent across all three syllables (right panel). In contrast, we predict that ΔF2 for /i-y/ and /ɯ-u/ in the Central dialect should be equivalent in the first two syllables, but decrease to below the coarticulatory threshold in the third syllable (left panel).

4.3 Results

4.3.2 Southern dialect

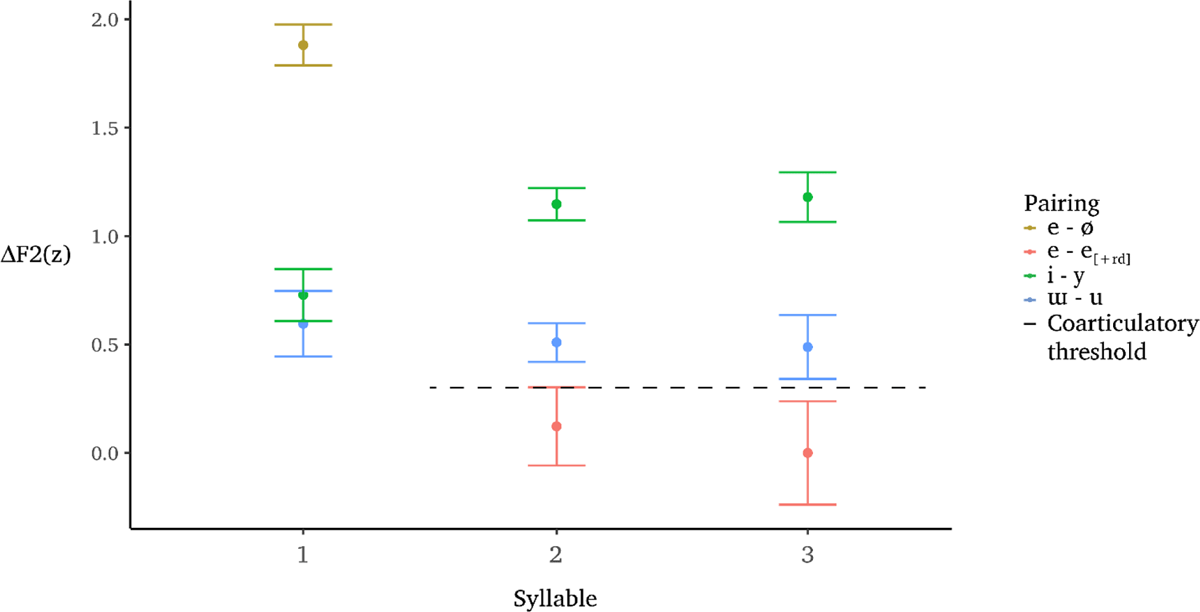
The coarticulatory threshold for the Southern dialect was 0.27z, which was the highest ΔF2 from the confidence interval around the mean of ΔF2 for second-syllable /e/ after [±round] vowels [ΔF2(119) = 0.08z; 95% confidence interval = [–0.11 – 0.27z]]. This threshold is marked in Figure 7 by the dotted line extending from the upper limit of the confidence interval around ΔF2 of e-e[+rd] in syllable two. Compared to the coarticulatory threshold, ΔF2/ɯ-u/ in syllable two was significantly greater [ΔF2/ɯ-u/ – threshold: t(572) = 4.42, p < .001]. Similarly, ΔF2 of /i-y/ in syllable two was also significantly greater than the threshold [ΔF2/i-y/ – threshold: t(842) = 9.68, p < .001]. Mean ΔF2 of /ɯ-u/ was 0.55z, with a confidence interval extending from 0.46 to 0.66z. Mean ΔF2 of /i-y/ was 1.11z, with a confidence interval ranging from 1.03 to 1.18z. These findings are evident in Figure 7, in which the confidence intervals around ΔF2/ɯ-u/ and ΔF2/i-y/ in syllable two do not overlap with the coarticulatory threshold. The significance of these acoustic differences persists in third-syllable vowel pairs, as well. Third-syllable high vowel pairs all exhibited significantly greater ΔF2 than the proposed coarticulatory threshold [ΔF2/ɯ-u/ – threshold: t(572) = 3.36, p < .001; ΔF2/i-y/ – threshold: t(521) = 5.93, p < .001].

Figure 7
Figure 7

ΔF2(z, with 95% confidence intervals) for each vowel pairing and syllable compared to the coarticulatory threshold in Southern Crimean Tatar.

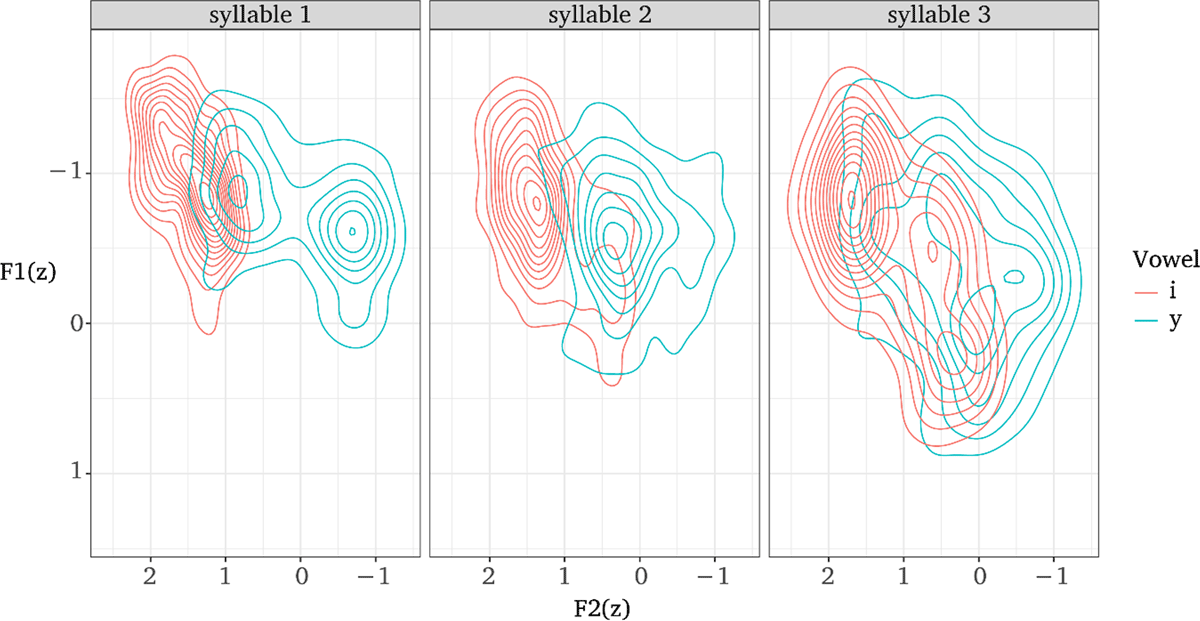
The data plotted in Figure 7 differ from the predictions laid out in Figure 6 in two ways. First, in Figure 6, ΔF2 of each pairing is similar in syllables one and two. While the difference between ΔF2 of /ɯ-u/ across syllables in Figure 7 is only slightly divergent, there is a notable decrease in ΔF2 of /i-y/ in syllable two. As noted above, there is a pattern of /y/-backing in initial syllables, where /y/ is realized as [y] after coronals, and as [u] elsewhere, e.g., /kyz/ [kuzʲ] ‘autumn’. Backing of initial-syllable /y/ is observable in the leftmost panel of the density plots in Figure 8.3 Observe that the distribution of /y/ (in green) includes two peaks that differ in F2, indicating bimodality. Of the 328 tokens of initial-syllable /y/, 137 were produced with a relatively back vowel, defined here as any vowel with F2 lower than 0z. As a result, ΔF2 of /i-y/ in syllable one in Figure 7 is inflated because it includes many data points for which ΔF2 reflects the difference between [i] and a phonetically back vowel [u].

Figure 8
Figure 8

F1-F2(z) density plots for /i/ and /y/ in syllables 1–3 in the Southern dialect.

Second, as in Figure 2, we expected ΔF2 of each high vowel pairing to hold constant in syllable three. Yet, in in Figure 7 third-syllable ΔF2 is less than ΔF2 in both syllables one and two. Again, the trend with /ɯ-u/ is not troubling because the differences are small, and could presumably be due to a simple contraction of the vowel space in non-initial syllables (Vayra & Fowler 1992; Tabain 2003). Thus, the issue is once again with the high front pairing, /i-y/.

Unlike the deviation from predictions just discussed for initial syllables, this does not fall out from any pattern of /y/ backing. Rather, the decrease in ΔF2 for third-syllable /i-y/ is due to centralization of /i/ to a vowel quality much closer to [ɨ] or [ə], as described in Kavitskaya (2010; 2013). To see this, compare the distributions for /i/ (red) in all three syllables in Figure 8. In the initial syllable, there is a single mode, with a median F2 value around 1.2z. In the second syllable, the median F2 value is similar, but also includes a number of data points with F2 between 0.8 and 0z, values notably absent from the leftmost panel of the figure. In the third syllable, the distribution is polymodal, with one mode around 1.7z, and two lesser modes around 0.6 and 0.4z. These additional modes reduce ΔF2 in the third syllable of Figure 7 by including a number of comparisons between [y] and [ɨ], which exhibit a smaller acoustic difference than [y] and [i]. Kavitskaya (2010; 2013) reports backing of historical *i to /ɨ/ in the Northern and Central dialects, but here we see phonetic backing in the Southern dialect. This backing differs from /y/-backing discussed above because it is less context-dependent, and more speaker-dependent. Table 1 reports these facts – Speakers 5 and 9 consistently produced front [i] while Speakers 6 and 7 variably produced [i] and [ɨ]. To reiterate, the centralization of /i/ in syllable three (and to a lesser degree, in syllable two) reduces ΔF2, which contributes to the decrease in ΔF2 reported in syllable three of Figure 7.

Table 1

By-speaker counts of centralization of third-syllable /i/ in the Southern dialect (n = 256).

Speaker (gender, age) Front (F2 > 1.0z) Central (F2 < 1.0z) Percent centralized
5 (female, 65) 60 0 0
6 (male, 51) 56 9 13.8
7 (male, 56) 28 37 56.9
9 (female, 62) 66 0 0
Total 210 46 18.0

A reviewer asks what the plot of the Southern Crimean Tatar data would look like if initial-syllable tokens of /y/ after dorsal obstruents, which induce backing, as well as centralized tokens of third-syllable /i/ were removed. After removing these independent patterns from the data, the resulting plot in Figure 9 conforms more closely to our predictions in Figure 6 – ΔF2 of both /i-y/ and /ɯ-u/ alternating pairs exhibits reasonable stability across all three syllables. While this sort of post-hoc analysis of variation in the data is not ideal, it suggests that once independent patterns involving the relevant alternating pairs are accounted for our method offers a plausible way to evaluate the extent of harmony.

Figure 9
Figure 9

A modified plot of ΔF2(z, with 95% confidence intervals) for each vowel pairing and syllable compared to the coarticulatory threshold in Southern Crimean Tatar. All initial-syllable tokens of /y/ following /k g/ were removed, as well as all third-syllable tokens of /i/ where F2(z) > 0.

Using ΔF2 and the coarticulatory effect of initial-syllable round vowels on second-syllable /e/ to operationalize rounding harmony in Crimean Tatar, we interpret the results from this subsection to support the case that the Southern dialect exhibits harmony on both second- and third-syllable high vowels. Previous research suggests that this result should contrast with the Central dialect, where ΔF2 of [+hi] vowels should exceed the coarticulatory threshold in second syllables only.

4.3.3 Central dialect

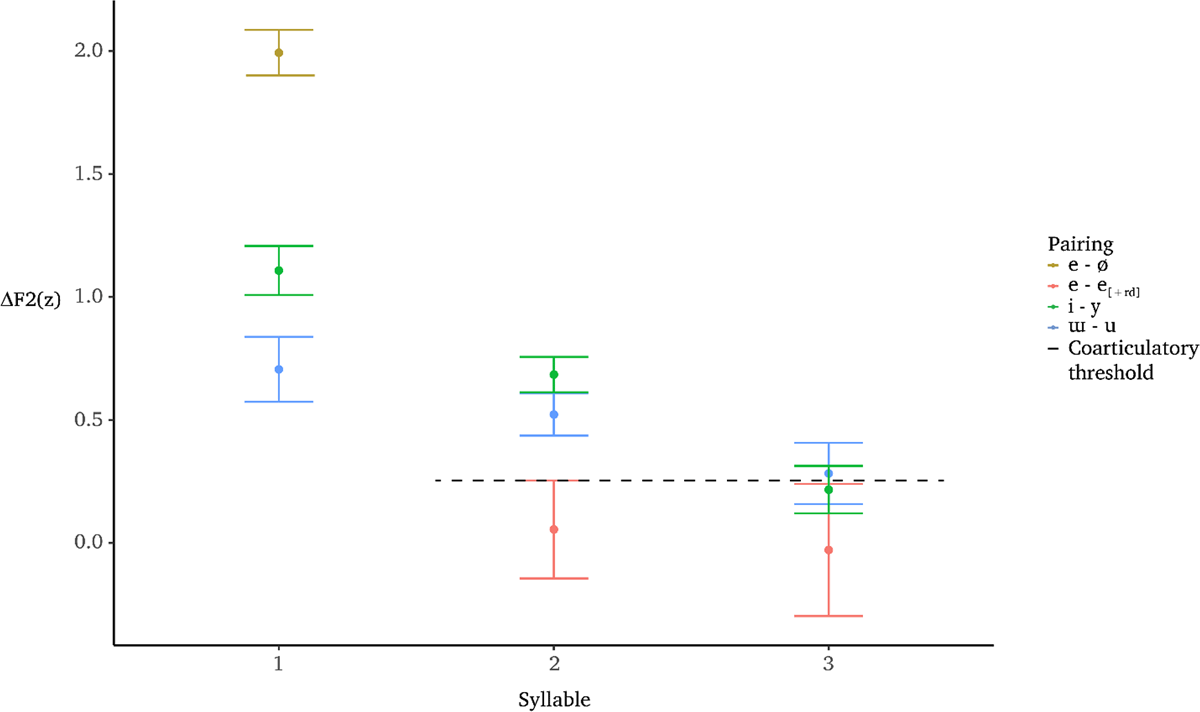
The coarticulatory threshold established for the Central dialect was 0.25z, derived from confidence interval around mean ΔF2 of the mid front vowel in [±round] contexts, [mean ΔF2(99) = 0.06z; 95% confidence interval = [–0.14 – 0.25z]]. It is clear in that ΔF2 for each of the two [+hi] vowel pairs in syllable two is significantly greater than the coarticulatory threshold [ΔF2/ɯ-u/ – threshold: t(461) = 6.11, p < .001; ΔF2/i-y/ – threshold: t(565) = 11.72, p < .001]. Observe that the confidence intervals for the second-syllable high vowel pairs do not overlap with the coarticulatory threshold. Mean ΔF2 of /ɯ-u/ was 0.52z, with a confidence interval extending from 0.44 to 0.61z. Mean ΔF2 of /i-y/ was 0.68z, with a confidence interval stretching from 0.61 to 0.76z. However, ΔF2 for each vowel pairing in syllable three was not significantly greater than the coarticulatory threshold [ΔF2u-ɯ – threshold: t(320) = 0.44, p = .33; ΔF2y-i – threshold: t(381)= –0.77, p = .80]. Visually, the fact that the coarticulatory threshold falls within each confidence interval supports the case that ΔF2 in syllable three does not exceed the magnitude of a proposed phonetic effect. For /ɯ-u/, the third-syllable mean ΔF2 was 0.28z, with a confidence interval from 0.16 to 0.41z. Similarly, the third-syllable mean ΔF2/ɯ-u/ was 0.23z, with a confidence interval from 0.12 to 0.31z.

Like Figure 7, the plot in Figure 10 deviates from our predictions because ΔF2 for the two high vowel pairings is smaller in syllable two than in syllable one. As discussed above, there is backing of /y/ to [u] in some initial-syllable contexts, which inflates ΔF2 in syllable one. The distribution of initial-syllable /y/ and /i/ is observable in the leftmost panel in Figure 11; in particular, note the bimodal distribution for /y/. Thus, initial-syllable ΔF2 of /i-y/ in Figure 10 is likely too high.

Figure 10
Figure 10

ΔF2(z, with 95% confidence intervals) for each vowel pairing and syllable compared to the coarticulatory threshold in Central Crimean Tatar.

Figure 11
Figure 11

F1-F2(z) density plots for /i/ and /y/ in syllables 1–3 in the Central dialect.

In addition, these two-dimensional density plots convey information about the harmonic pairings not available in Figure 10. For instance, consider also the distribution of /ɯ/ and /u/ shown in Figure 12. It is not entirely obvious from Figure 10 that the rounding of second-syllable /ɯ/ is phonological while rounding of third-syllable /ɯ/ is not. In Figure 12, we see the most consistent difference in F2 in the initial syllable, with robust but slightly diminished F2 distinctions (i.e., more overlapping distributions) in the second syllable, with almost complete overlap in F2 in the third syllable. Additionally though, we see that /ɯ/ is typically produced with greater F1 than /u/. This observation holds in the first two syllables, where underlying and derived /u/ exhibit smaller F1 than /ɯ/. However, in the third syllable, this difference in F1 is lost, and both high back vowels are produced with F1 that is generally consistent with /ɯ/. Thus, third-syllable high back vowels show no distinction in F1 or F2, further supporting the case that there is a phonological difference between the effects on second- and third-syllable high vowels.

Figure 12
Figure 12

F1-F2(z) density plots for /ɯ/ and /u/ in syllables 1–3 in the Central dialect.

At the request of a reviewer, we present a plot of ΔF2 from our Central data. In this case, only tokens of backed /y/ after dorsal obstruents were culled from the dataset. Like the Southern data in Figure 9, the modified ΔF2 plot in Figure 13 conforms more closely to our initial predictions – ΔF2 of /i-y/ and /ɯ-u/ clearly exceeds the coarticulatory threshold in syllables one and two, but is notably diminished in syllable three.

Figure 13
Figure 13

A modified plot of ΔF2(z, with 95% confidence intervals) for each vowel pairing and syllable compared to the coarticulatory threshold in Central Crimean Tatar. All initial-syllable tokens of /y/ following /k g/ were removed.

Methodologically, we have presented one way to assess the presence or absence of harmony from acoustic data. ΔF2 values have provided useful information to corroborate previous descriptions of rounding harmony in Southern and Central Crimean Tatar. However, the method employed here does not entirely answer the research question, as other acoustic information was necessary to determine the extent of rounding harmony in each dialect. Also, a reviewer asks whether it would be possible to identify acoustic correlates of the onset, trajectory, and offset of lip rounding as an alternative way to probe the domain of phonological versus phonetic lip rounding. This methodology is employed in work like Myers (2003) to identify f0 turning points for tone. However, there is a key difference between f0 and F2 – F2 is affected by intervening consonants in a manner quite distinct from the small perturbations in f0 from consonants. While such a method could help understand the shift from phonological assimilation to coarticulation and the phonology-phonetics interface, it requires kinematic data that are unavailable at present.

Concluding this section, ΔF2 of each high vowel pair was significantly greater than the coarticulatory threshold in syllable two but not in syllable three. This suggests the veracity of previous descriptions of the Central dialect, in which rounding spreads to a single high-vowel target only. In short, our results are generally consistent with the claim that the Southern dialect exhibits iterative harmony while the Central dialects exhibits non-iterative harmony.

5 Further evidence: invariantly round suffixes

Up to this point, the paper has focused only on spreading from an initial-syllable trigger, e.g., [tuz-luɣ-ɯ] ‘salt-nmlzr-poss.3.’ In many of the words discussed thus far, the application of harmony results in suffix alternations. However, there are a number of suffixes that do not alternate for rounding in the language. One class of non-alternating suffixes is always produced with a high unrounded vowel, as in the accusative and genitive case-marking suffixes, e.g., [kyz-ni] ‘autumn-acc’ and [tuz-nɯŋ] ‘salt-gen.’ A second class of non-alternating suffixes is always produced with a round vowel.4 These suffixes also trigger lip rounding, and in the Central dialect, this lip rounding extends to a single following high vowel only. For instance, the gerundial and collective suffixes are always [+round], although they do alternate for backness. The gerundial suffix alternates between [yv] and [uv] while the collective suffix alternates between [jy] and [ju]. A number of examples within our corpus of fieldwork data exhibit harmony after ger and coll, shown in (11).5

    1. (11)
    1. Rounding harmony after ger andcoll
    1. a.
    2. b.
    3. c.
    4. d.
    5. e.
    6. f.
    7. g.
    1. /as-uv-lɯ/
    2. /aʧ-uv-ɯ/
    3. /aʧ-uv-ɯ-dan/
    4. /qoj-uv-ɯ/
    5. /bir-ju-ɯ-n/
    6. /ek-ju-ɯ-n/
    7. /yʧ-ju-ɯ-n/
    1. [as-uv-lu]
    2. [aʧ-uv-u]
    3. [aʧ-uv-un-dan]
    4. [qoj-uv-u]
    5. [bir-jy-y-n]
    6. [ek-jy-y-n]
    7. [yʧ-jy-y-n]
    1. ‘hang-ger.adj’
    2. ‘open-ger-poss.3’
    3. ‘open-ger-poss.3-abl’
    4. ‘put-ger-poss.3’
    5. ‘one-coll-poss.3-acc’
    6. ‘two-coll-poss.3-acc’
    7. ‘three-coll-poss.3-acc’

In (11a,b,e,f), we see that round vowels may occur in almost any two-syllable window within the word. Rounding need not be triggered by the initial syllable, and it certainly does not need to extend to the final syllable. Moreover, rounding may be present in three consecutive syllables if the first two round vowels derive from two different sources (11d,g). As such, it is clear that rounding is not limited to the first two syllables only. In the Central dialect, rounding spreads rightward to one high vowel from any underlyingly [+round] vowel, root-internal or suffixal.

6 Is non-iterativity in Central Crimean Tatar emergent?

We have already suggested that round spreading is non-iterative, and as such is not obviously amenable to the types of analyses put forth in Kaplan (2008). In this section we argue against possible attempts to reconcile the data from the Central dialect with Kaplan’s claim in (1).

6.1 Stress

One might attempt to explain the extent of harmony in the Central dialect by referencing stress and metrical footing. The argument goes as follows: if stress falls on the leftmost syllable, then it is possible to construct a left-aligned trochee, making rounding harmony in Central Crimean Tatar foot-bounded. Alternatively, if stress is peninitial, then the apparent non-iterativity of harmony could derive from a metaphony-like spreading up to the stressed syllable. Problematically for both potential stress-based analyses, previous work argues that primary stress falls on the rightmost syllable (Sevortjan 1966; Baski 1986; Kavitskaya 2010; 2013; Memetov 2012; 2013). Most of these authors also report secondary stress on the initial syllable of words of at least three syllables in length. According to Baski (1986:119), primary and secondary stressed syllables are evident by their resistance to phonetic reduction and elision. Based on our own experience with the language, however, high vowels may be reduced to the point of elision in all non-final syllables, with an even greater tendency to elide initial-syllable high vowels, consistent with Kavitskaya (2004; 2010; 2013).

Regardless of where stress falls, the data from Section 5 show that a round vowel may trigger harmony from any non-final syllable. If one attempts to align harmony to primary stress at the right edge of the word, a single, binary foot cannot coincide with rounding harmony in a word like tuz.(lu.ɣɯ́) ‘salt-nmlzr-poss.3s’. If a binary foot is constructed at the left edge of the word (iambic or trochaic) based on secondary stress, it cannot account for words like (qo.ju).vu ‘put-ger-poss.3’. Since rounding harmony can be triggered by any non-final syllable, no metrically-oriented analysis can successfully define the domain of harmony (cf. Piggott 1996). Our own acoustic investigations of stress in the language provide little evidence for any form of word-level stress.

6.2 Other possibilities

In addition to stress, work in Lexical Phonology (Mohanan 1982; Kiparsky 1985) has demonstrated that the domain of some phonological patterns is definable in terms of morphological constituency. In the realm of vowel harmony, work has shown that lexical strata play a role in the application of some patterns (e.g., Kiparsky 1985; Lahiri 2000; McPherson & Hayes 2016). In the present case, though, no such morphological analysis is possible because the extent of harmony extends one syllable rightward from an underlying [+round] vowel regardless of its position in the word. Thus, rounding may operate within a root, [qoruv] ‘security’, from a root to a suffix, [tuz-luq] ‘salt-nmlzr’, or from a suffix to another suffix, [aʧ-uv-u] ‘open-ger-poss.3s.’ Moreover, each suffix’s ability to participate in round spreading depends on its proximity to a [+round] trigger regardless of any particular morphological strata. More concretely, if the third-person possessive suffix is within a stratum subject to rounding harmony, it should always alternate for harmony. Yet, in words like [tuz-luɣ-ɯ] ‘salt-nmlzr-poss.3s’ we see that the possessive suffix is not subject to harmony when separated from the original trigger by an intervening syllable. Since harmony is not definable in terms of any particular lexical strata or sub-word morphological domains, we conclude that no morphological analysis will be able to define the domain of rounding harmony in the Central dialect.

Recall from above that some work analyzes word-internal harmony as the result of prominence-targeting patterns (Walker 2005; 2011; Kaplan 2008; 2015). In these cases, harmony is initiated by a weak position, spreading the harmonic feature to some prominent position in order to satisfy some licensing requirement. In Central Crimean Tatar, though, there is no evidence that triggers or targets exhibit any particular prosodic weakness or prominence to drive spreading. Instead, non-iterative spreading obtains on high vowels in any position.

We know of no other possible sub-word domains that are coextensive with, or that could motivate non-iterative harmony in the language. For instance, we are unaware of any minimality requirements in the language, although content words are almost always CVC or longer. If this strong tendency is encoded in the grammar, however, it would lend support for the mora, but not for any syllable-based generalization to define the application of rounding harmony.

Finally, in contrast to cases of tone shifting and tone spreading (Section 2.4), there is no phonetic reason for a lip rounding gesture to require a two-syllable domain. In fact, phonetic research on lip rounding has consistently found that lip rounding is often achieved before the onset of the target segment (e.g., Bell-Berti & Harris 1982; Perkell & Matthies 1992), undermining any potential analysis predicated on sluggish articulation.

For these reasons we conclude that non-iterative rounding harmony in Central Crimean Tatar is truly grammatical, and not emergent. In the next section we discuss the analytical import of this finding.

7 Analytical implications

The data discussed in Sections 4–6 suggest that non-iterativity in Crimean Tatar is not epiphenomenal. The domain of harmony is not derivable from prosodic, morphological, or phonetic forces, but must be a phonological fact, deserving a formal account. In this section we compare several approaches to feature spreading, discussing how non-iterativity is derived in each.

7.1 Rule-based phonology

We use the term rule-based phonology to refer to a system of ordered rules, like Chomsky and Halle (1968). We acknowledge that there are many different rule-based theories that have developed during the last half century, but for our purposes, the essential architecture debated during the late 60’s and early 70’s is sufficiently articulated to account for the facts at hand. In any rule-based theory that has access to the feature [±iterative] or may parametrically vary the direction of rule application, the Central Crimean Tatar pattern is easily derivable (Johnson 1972; Howard 1973; Jensen & Stong-Jensen 1973; Anderson 1974; Kenstowicz & Kisseberth 1979). Either the rule motivating harmony, [+syllabic,+high] → [+round] / [+syllabic, + round] C0 ____, is tagged as [–iterative], or the string is evaluated from right to left. If directional evaluation is used, non-iterative spreading in /tuz-lɯq-ɯ/ is due to the fact that the rule evaluates /…lɯqɯ/ before it has access to the rounding feature of the initial syllable, outputting third-syllable [ɯ]. The second-syllable /ɯ/ is output as [u] because, at this next step in the evaluation of the harmony rule, the rule has access to the [+round] feature of the initial-syllable vowel. Non-iterativity is thus not problematic for a relatively standard rule-based formalism.

One question for such a formalism is why non-iterative patterns appear to be far less frequent than iterative ones. Given a rule feature [±iterative], one might predict that iterative and non-iterative patterns occur relatively freely across the world’s languages, but this is not the case. During our research, we found that the vast majority of attested patterns are iterative within some domain, often the word. We do not yet have concrete numbers, but we would estimate that there are hundreds of unambiguously iterative patterns, while there are only a handful of unambiguously non-iterative patterns. This typological skew, however, is only relevant for theories that view typological asymmetries as within the purview of phonological theory (see e.g., Hale & Reiss 2008; Vaux & Myler 2017 for discussion). For other theories, these facts are immaterial, but to the extent that a theory expects the phonological grammar to interact directly with typological frequency, the typological rarity of non-iterativity deserves an explanation.

7.2 Constraint-based analysis

The impetus for Kaplan’s emergent non-iterativity hypothesis in (1) is the architectural challenge of deriving non-iterativity in OT (see Kisseberth 2007; Vaux 2008 for further discussion). Consider the interaction of two constraints, ∀-Harmony-R([+rd],V) (12) and Dep-Link-[+rd] (13). The harmony-driving constraint, adapted from Walker (2011) motivates rightward harmony while Dep-Link[+rd] penalizes any form of spreading via autosegmental linkage.

    1. (12)
    1. ∀-Harmony-R([+rd],V)
    1. given a word in which a [+round] autosegment r is affiliated with some vowel vr, assign a violation to every vowel to the right of vr that is not associated with r.
    1. (13)
    1. Dep-Link[+rd]
    1. assign a violation to every association line present in the output that is absent in the input

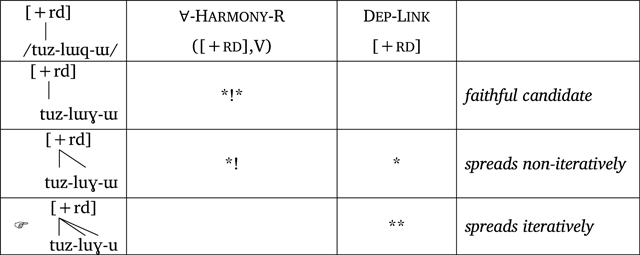
If ∀-Harmony.R outranks Dep-Link, as in (14), iterative harmony is predicted; if the ranking is reversed, no harmony is predicted. Thus, in (14) the non-iterative candidate is collectively harmonically bounded (Samek-Lodovici & Prince 1999). There is no simple ranking of the sort of typical markedness and faithfulness constraints to generate the particular pattern in Central Crimean Tatar, a fact which also holds for other constraint-based theories (e.g., Harmonic Grammar; Legendre et al. 1990).

    1. (14)

However, this problem is not insurmountable. Observe that the iterative spreading candidate in (14) contains vowels that are linked to the same autosegment but are not syllable-adjacent. Specifically, the initial syllable [tuz] and the third-syllable [ɣu] are separated by a syllable [lu]. While this multiple linkage is bridged by the link to the second-syllable vowel, this structure involves some similarities with gapped configurations, which have been the subject of much discussion in autosegmental research (McCarthy 1984; Ringen 1988; Vago 1988; Archangeli & Pulleyblank 1994; Odden 1994).

At its core, a well-formedness condition (or violable constraint) on gapped configurations involves several conditions. Given a tier containing the elements x, y, and z such that x < y < z, and some autosegment [F], there are two conditions necessary to produce a gapped structure: first, linkage of a single autosegment of [F] to two elements, x and z, which are not adjacent; and second, no linkage between the relevant autosegment [F] and y. If only the first is satisfied, long-distance linkage, without the failure to link to y, then this is well-formed, and is simply an instance of iterative feature spreading. If only the second is satisfied, but not by spreading, this is also unproblematic. For instance, the Turkish root [protesto] ‘protest’ has [+round] underlyingly linked to the first- and third-syllable vowels.

The first precondition for gapped configurations, linkage of non-adjacent elements to the same autosegment, is the key to deriving non-iterativity. We introduce a constraint, Adjacency, in (15) that militates against such shared linkage among non-adjacent elements. As far as we know, this particular constraint is not described in previous work, despite some similar proposals in the literature (Cassimjee & Kisseberth 1998; Topintzi & van Oostendorp 2009; Jurgec 2011; Key & Bickmore 2014). Though it is not crucial, this constraint assigns violations to each autosegment that is linked to non-adjacent vowels. It does not assign violations to the links themselves. Consequently, it does not distinguish between a token of [F] linked to three elements versus [F] linked to four elements.

    1. (15)
    1. Adjacency[+rd]
    1. given a string Y consisting of v1…vn and a [+round] autosegment, assign a violation to every token of [+round] that is linked to non-adjacent vowels, e.g. vy and vy+2; vy–2 and vy+2 ; vy–1 and vy+1.

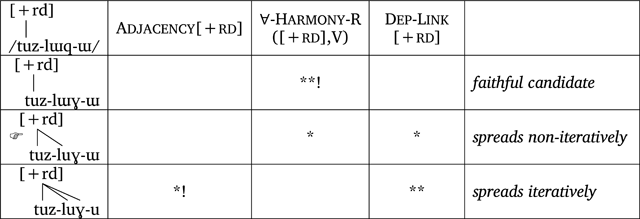
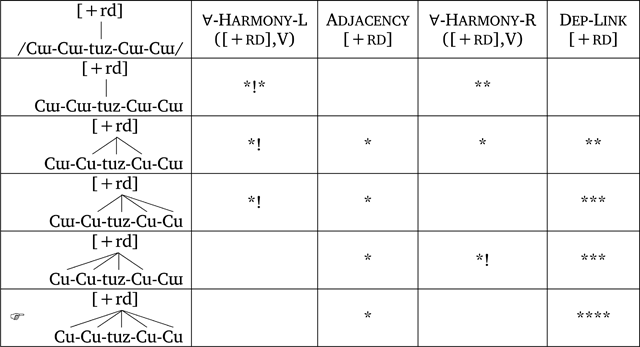
Highly-ranked Adjacency constrains round spreading in Central Crimean Tatar to being non-iterative, seen in (16). The iterative spreading candidate incurs a fatal violation of Adjacency, leaving the faithful and non-iterative spreading candidates to be evaluated by the harmony-driving constraint, which prefers non-iterative harmony over no harmony.

    1. (16)

In addition to the basic pattern, where spreading is initiated by the root, our analysis is able to account for spreading from [+round] suffixes like ger and coll in (11). The fact that /qoj/ and /uv/ are each affiliated with their own unique [+round] autosegment is crucial to generate spreading from the [+round] suffix in (17). As a result, the sequence of three consecutive round vowels in [qoj-uv-u] does not violate Adjacency because only the last two are linked to the same token of [+round]. Observe that since the harmony-driving constraint assigns violations to every vowel to the right of the trigger that is not affiliated with the trigger’s [+round] autosegment, three violations are incurred by the faithful candidate while only two are incurred by the candidate with spreading from ger. To save space, we abbreviate [+rd] as [+] in (17). While it is possible to delete the autosegment affiliated with ger to reduce the number of violations of ∀-Harmony-R, we assume a highly-ranked faithfulness constraint protecting that suffix’s [+round] autosegment, in parallel with another constraint protecting the [+round] autosegment affiliated with the initial syllable.

    1. (17)

7.2.2 Typology

Returning to the issue of typology, one of OT’s core assumptions is that the typology of permuted rankings should generate a reasonable fit to attested data. Some work goes beyond this, suggesting that the frequency of a pattern within and across languages can be derived from the relative number of rankings that generate that pattern (Anttila 1997; Coetzee 2004; Bane & Riggle 2008; Riggle 2010; Coetzee & Pater 2011). If this view of the grammar is adopted, then it becomes possible to evaluate not only whether an analysis can generate iterative and non-iterative spreading, but also whether the analysis can model the typological skew toward iterative spreading patterns noted at the end of Section 7.1 – the number of iterative harmonies is disproportionately larger than the number of truly non-iterative patterns described in the world’s languages.

We investigated the factorial typology generated by the three constraints above using OTSoft (Hayes, Tesar & Zuraw 2011). Three types of candidates were considered: no spreading, iterative spreading, and non-iterative spreading. With this set of constraints, there are six possible rankings. Three of these generate a language with no spreading (18a–c); two generate a language with iterative spreading (18e,f); and only one generates a language with non-iterative spreading (18d) – the ranking instantiated in (16) and (17). Given the relative infrequency of non-iterative harmony, these constraints should generate non-iterative harmony far less often than iterative harmony.

    1. (18)
    1. Factorial typology
    1. a.
    2. b.
    3. c.
    4. d.
    5. e.
    6. f.
    1. Dep-Link >> Adjacency >> ∀-Harmony
    2. Dep-Link >> ∀-Harmony >> Dep-Link
    3. Adjacency >> Dep-Link >> ∀-Harmony
    4. Adjacency > > ∀-Harmony >> Dep-Link
    5. ∀-Harmony >>Adjacency >> Dep-Link
    6. ∀-Harmony >>Dep-Link >> Adjacency
    1. no spreading
    2. no spreading
    3. no spreading
    4. non-iterative spreading
    5. iterative spreading
    6. iterative spreading

The OT account above enables the analyst to fit a model to not only a set of possible languages, but also to their relative frequencies. If the grammar is viewed as responsible for predicting typology, this OT analysis predicts higher incidence of iterative over non-iterative harmony. While we consider this to be a favorable result, there is still much to be desired. If one were to naively derive frequencies from these, they would still fail to fit the attested asymmetry. We suspect that the actual ratio of iterative to non-iterative harmony is much closer to 100:1 than 2:1, the basic ratio predicted by this analysis.

7.3 Discussion

7.3.1 Roots

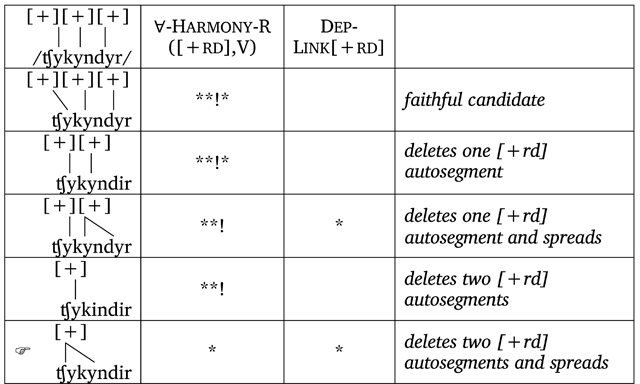
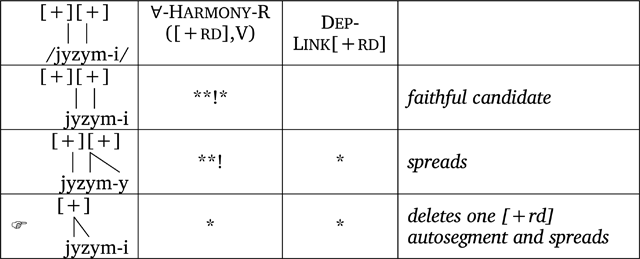
The OT analysis sketched above makes predictions about the production of roots as well as polymorphemic words. As a reviewer notes, the OT analysis predicts that, because only initial-syllable faithfulness and not a more general root faithfulness constraint is active, no trisyllabic roots should exist in the Central dialect with rounding on all three syllables. We mentioned in Section 4.1.2 that disyllabic roots like [jyzym] ‘grape’ do not spreading rounding onto a suffix, e.g., [jyzym-i] ‘grape-poss.3s.’ The absence of spreading here indicates that there is only one [+round] autosegment associated with polysyllabic roots of this sort, since root-internal second syllables behave exactly like suffixal second syllables. The examples in (19) demonstrate that trisyllabic roots, in accordance with this prediction, only have rounding on the initial two syllables in the Central dialect.6 These facts entail that, completely independent of a necessary initial-syllable faithfulness constraint, Adjacency outranks root faithfulness.

    1. (19)
    1. Polysyllabic roots with a two-syllable domain for rounding
    1. a.
    2. b.
    3. c.
    4. d.
    5. e.
    1. jyzym
    2. kølyk
    3. xusus
    4. ʧykyndir
    5. ʤumxuriet
    1. ‘grape’
    2. ‘livestock’
    3. ‘answer’
    4. ‘beet’ (ʧykyndyr ~ yʧkyndyr in the Southern dialect)
    5. ‘republic’

To see the sufficiency of our constraint ranking to generate the correct outputs in words with polysyllabic roots, consider the tableaux in (20) and (21). In (20) we demonstrate that the correct output [ʧykyndir] is derivable even from an input with three [+rd] autosegments. In (21), a disyllabic domain for harmony in [jyzym-i] is generated from an input with two [+rd] autosegments. In each case, the fact that ∀-Harmony demands association with a particular autosegment penalizes multiple autosegments in much the same way a markedness constraint on [+rd] autosegments would, preferring candidates that delete unnecessary autosegments and spread non-iteratively.

    1. (20)
    1. (21)

7.3.2 Directionality

Rule- and constraint-based analyses make substantially different predictions concerning the general interaction between iterativity and directionality. In a rule-based approach, it is possible to derive bidirectional non-iterativity by marking a rule motivating bidirectional harmony as [–iterative].7 Consider the rule in (22).

    1. (22)

Given an underlying form like /iCiCyCiCi/, this rule predicts the surface form [iCyCyCyCi]. However, bidirectional non-iterative spreading cannot be generated by the analysis laid out in Section 7.2. Any three consecutive elements linked to a single token of [F] will violate Adjacency without respect for which element was underlyingly linked to [F]. Thus, this cannot distinguish between unidirectional iterative harmony /[+F][–F][–F]/ → [+F][+F][+F] and bidirectional non-iterative harmony /[–F][+F][–F]/ → [+F][+F][+F]. This is an interesting difference between a rule-based analysis and our analysis, but we are not sure which prediction is superior. We know of no attested bidirectional non-iterative patterns (see also Piggott 1996:158). That being said, it is incorrect to say that constraint-based theories are simply incapable of generating something similar. This really depends on the representational assumptions made as well as the particular constraints invoked, but under the analysis just discussed, it is impossible.

In addition to bidirectional non-iterativity, if iterativity is a feature of rules, then it is possible to generate a language with non-iterative harmony in one direction but iterative harmony in the other direction. The rule-based analysis is clear-cut; one of the two rules driving harmony is simply tagged as [–iterative]. Given the constraints discussed above, this sort of pattern also cannot be generated. For instance, if we imagine a language like Crimean Tatar, except that both prefixation and suffixation are productive. In this language leftward harmony is iterative, but in the rightward direction, harmony is non-iterative.

If we introduce a high-ranking leftward harmony-driver, ∀-Harmony-L without further modification to the analysis, consider the effects in (23). By ranking ∀-Harmony-L over Adjacency, the force of Adjacency, even over rightward harmony, is entirely suppressed. Since satisfying ∀-Harmony-L requires violating Adjacency, and since Adjacency is non-directional, bidirectional iterativity is generated. While it would be possible to split Adjacency up into directional variants, this is not appealing.

    1. (23)

We know of no patterns like this hypothetical asymmetrical pattern in natural language. The closest example we know of comes from ATR harmony in Nawuri (Casali 2002; though see the Northern Palestinian Arabic data in Davis 1995). In Nawuri, ATR harmony operates regularly within words, but across word boundaries a directional asymmetry emerges. In the leftward direction, harmony may affect a number of vowels. In the rightward direction, though, harmony may only affect a single [+hi] vowel. Of note, the Nawuri pattern is actually not problematic for Kaplan’s analysis due to the relevance of word boundaries (Kaplan 2008:275).

7.3.3 Transparency

Since our Adjacency constraint subsumes a constraint on gapped configurations (Itô, Mester & Padgett 1995), it is also violated by transparency in feature spreading. Consequently, this constraint predicts that, all else being equal, there should be no non-iterative patterns that involve transparency. As an example of such a pattern, if non-high vowels were skipped by rounding harmony in Central Crimean Tatar, we could generate /qulaq-lɯq-ɯ/ *[qulaq-luɣ-ɯ] ‘ear-nmzlr-poss.3’ rather than the attested [qulaq-lɯɣ-ɯ]. A similar case is found in C’Lela, where height harmony affects a single target and exhibits transparency (Dettweiler 2000). However, the trigger is always root-internal while the target is always word-final, which makes the pattern similar to Bengali because there are restrictions such that triggers and targets form two non-intersecting classes (Chandlee 2021). While non-iterativity is completely independent of transparency in a rule-based analysis, the two are inseparable under our OT analysis.

Both rule- and constraint-based theories have formal tools that are useful for analyzing non-iterative spreading. However, they make different predictions regarding typological frequency (if one desires that from a formal analysis), the relationship between boundaries and feature spreading, and multidirectional feature spreading.

7.4 What is non-iterativity?

Asking ‘what is non-iterativity?’ at the end of a paper on the topic may seem obtuse, but comparing rule- and constraint-based theories requires some analytical context, which we hope to have provided by this point. In a rule-based theory, non-iterativity means a rule can apply only once, or alternatively that it cannot feed itself. In a constraint-based theory no direct equivalent is available, because as Kaplan (2008:2) rightly notes, “[w]hen a process applies (non)iteratively, it does so because that happens to be the best way to satisfy some output desideratum, not because the process is specifically required to be (non)iterative.” Thus, there is no single intensional characterization of non-iterative feature spreading available to both theories. In this regard, we agree with Kaplan – feature spreading in Central Crimean Tatar terminates after a single application, not because the harmony driver dictates it do so, but because another constraint, Adjacency, militates against further spreading. We diverge from Kaplan, though, because the constraint that curtails further spreading is not independently necessary to analyze the phonology of the language, as is the case in many of the languages discussed in Kaplan (2008). Instead, the interaction between Adjacency and ∀-Harmony encodes a parameter-like setting in the grammar – when Adjacency >> ∀-Harmony, feature spreading is non-iterative; when ∀-Harmony >> Adjacency, feature spreading is iterative, though note the more complex interactions in (23).

Diachronically, in Kavitskaya & McCollum (to appear) we argue that non-iterative rounding harmony in Turkic represents an intermediate stage between no harmony and iterative harmony (see also McCollum to appear). In effect, non-iterative harmony forms one possible intermediate stage between phonetic coarticulation and fully operative (iterative) harmony. Phonologization of coarticulation (Hyman 1976; 2013) does not result in the sort of harmony attested in languages like Finnish, Turkish, and Kinande, but rather the sort of harmony found in Central Crimean Tatar. In like manner, non-iterativity is one possible outcome of the erosion of a more robust, iterative pattern. This is precisely the situation in Central Crimean Tatar, as the texts recorded in Radlov (1896) exhibit iterative rounding harmony in the Central dialect. Thus, the existence of non-iterativity has implications for both the synchronic and diachronic analysis of harmony. The categories employed to describe the synchronic nature of these patterns inform a model of language change. Conversely, models of language change may inform why non-iterative patterns appear to be significantly less frequently attested than iterative patterns.

8 Other cases of non-iterative feature spreading

At this point it is helpful to broaden our perspective and consider other reported cases of non-iterativity. If non-iterative feature spreading is real, then it should not be surprising to find it attested in other languages. Two related languages, Karakalpak (Menges 1947) and Kazakh (Balakaev 1962), display rounding harmony patterns almost identical to that in Central Crimean Tatar. In these languages, underlying [+rd] vowels, regardless of position, trigger harmony on a single following high vowel, e.g., Kazakh /tʊr-mɯs-ɯ-nɯŋ/ [tʊr-mʊs-ɯ-nɯŋ] ‘live-nmlzr-poss.3-gen’; /ber-ʊw-ɯ/ [ber-ʏw-ʏ] ‘give-ger-poss.3.’

Along with these genetically related languages, several varieties of Greek spoken in Asia Minor exhibit non-iterative regressive backness harmony (van Oostendorp & Revithiadou 2005). In Megisti Greek, final vowels trigger assimilation of penultimate vowels, irrespective of stress placement, e.g., /zervjá/ [zarvjá] ‘left’; /zílj-a/ [zúlja] ‘jealousy-nom.f’; /áɡir-a/ [áɡura] ‘anchor-nom.f.’

A number of phrasal harmonies are also reportedly non-iterative (Downing 2018; Kaisse 2019; Obiri-Yeboah & Rose 2022; Downing & Krämer to appear). For instance, consider across-word ATR harmony in Akan in (24). Observe the serial verb constructions in (24a,b) from (Ampofo & Rasin 2021), as well as the data from Kügler (2015) in (24c,d). In each case, the [+ATR] value of the following noun assimilates the final vowel of the preceding verb while all other vowels surface faithfully as [–ATR].

    1. (24)
    1. ATR harmony in Akan constructions8
    1. a.
    2. b.
    3. c.
    4. d.
    1. /tɔ fa kɔ/
    2. /tɔ fa di/
    3. /ɔ-pɛ sika/
    4. /ɔ-tɕɪrɛ kube/
    1. [tɔ fa kɔ]
    2. [tɔ fæ di]
    3. [ɔ̀-pè sìká]
    4. [ɔ̀-tɕɪ̀ré kùbé]
    1. ‘buy, take, and go’
    2. ‘buy, take, and eat’
    3. ‘3s-like money’
    4. ‘3s-show coconut’

Kaplan (2008) suggests that languages with phrasal spreading patterns like that found in Akan are derivable if one assumes that feature domains are headed (Smolensky 2006; Jurgec 2011). Parallel to the Nonfinality constraint that bans prosodic heads on word-final syllables, Kaplan proposes a constraint banning word-final heads of harmonic domains. While discussing a rule-based formalization of data from several languages, Kaplan observes that a rule that contains a word boundary in its context, e.g., V → [+F] / ____ C0# #C0[+F], need not refer to iterativity in most cases, since the word boundary preempts any necessary reference to rule reapplication. However, Kaplan notes that such a rule predicts iterativity across a string of monosyllabic words (2008:275). Ampofo & Rasin’s (2021) Akan data in (24b) bear directly on this prediction, demonstrating that it is inconsistent with the Akan data, since only a single preceding monosyllabic word assimilates to [+ATR]. This is crucially different than the iterative assimilation found across monosyllables in Vata (Kaye 1982), which is predicted by Kaplan’s analysis.

Another example of non-iterative spreading is found in tone. Cases of non-iterative high tone spreading in Bantu are well known (Kisseberth & Odden 2003; Key & Bickmore 2014), but we know of one case of non-iterative low tone spreading. In the Eagle dialect of Hän (Athabaskan), low tone spreads rightward to the immediately following tone-bearing unit (Manker 2014; Lehman 2018). In (25a), in the absence of any underlying low tone, all tone-bearing units surface with a default high tone. In (25b) though, the low tone associated with /žùr̥/ ‘wolf’ spreads rightward onto /ɬąy/ ‘dog’, and in (25c) that same low tone spreads onto the first tone-bearing unit of the verb.

    1. (25)
    1. Low tone spreading in Hän
    1. a.
    2. b.
    3. c.
    1. /čæː ɬąy nohʔį/
    2. /žùr̥ ɬąy nohʔį/
    3. /ɬąy žùr̥ nohʔį/
    1. [čǽː ɬą́y nóhʔį́]
    2. [žùr̥ ɬą̀y nóhʔį́]
    3. [ɬą́y žùr̥ nòhʔį́]
    1. “The boy sees the dog”
    2. “The wolf sees the dog”
    3. “The dog sees the wolf”

Under Kaplan’s proposal, non-iterative tone spreading should be limited to high tone spreading due to the lag typically needed to realize a high or rising tone (Myers 1999; 2003; Xu 2001). Yet, in Hän the spreading tone is low, which makes Kaplan’s analysis less tenable. In addition, there are two pieces of evidence that support the non-iterativity of low tone spreading in Hän. First, spectrographic evidence in Lehman (2018) indicates that a high tone is phonetically realized within the target syllable, removing any peak delay-based explanation of the pattern. If we were to attempt to analyze L spreading in (25b,c) as peak delay, we would not be able to account for the realization of H on the initial syllable in (25a). Second, Manker (2014) and Lehman (2018) discuss properties of this pattern that further suggest the pattern is not reducible to phonetic implementation – low tone spreading is sensitive to the OCP as well as lexical stress. Low tones do not spread onto lexically stressed tone-bearing units or when a second underlying low is two tone-bearing units away.

These cases of non-iterativity in ATR harmony, backness harmony, and low tone spreading serve to demonstrate that non-iterativity is not limited to Central Crimean Tatar. We conclude that these patterns further bolster the case that iterativity and non-iterativity must be encoded in the phonological grammar.

9 Conclusion

In this paper we have verified impressionistic reports of vowel harmony in Crimean Tatar with a production study, finding that the extent of rounding harmony in the Central dialect is smaller than in the Southern dialect. We interpret this result to support the case that rounding harmony in Central Crimean Tatar is non-iterative. We discuss possible ways to derive non-iterativity from other facts about the language, showing that these fail. The failure of these possible reanalyses dictates the inclusion of some relatively direct encoding of non-iterativity in the grammar. We illustrate possible analyses of true non-iterative spreading in rule- and constraint-based theories, discussing the different predictions made by each. Herein we were only able to marshal data from a handful of non-iterative spreading patterns. Looking forward, we expect that further investigation will help us understand how the predictions of these various formalisms compare with the typology of non-iterative feature spreading more generally.

Notes

  1. There is also progressive height harmony from the root that forces /ɛ/ to raise to [i] if the root is [+high], as in (2b,c,e,f). This separate harmony pattern is orthogonal to foot-bounded fronting harmony. [^]
  2. In some cases, H shifts left to the initial-syllable, but these are not germane for the topic at hand. [^]
  3. The two-dimensional density plot in Figure 8, also called a contour plot, represents the distribution of some set of data points along two continuous dimensions, here F1 and F2. The method employed uses kernel density estimation to generate a probability distribution function. [^]
  4. For a fuller list of alternating and non-alternating suffixes, see Kavitskaya (2010:39–43, 54–56, 59). [^]
  5. Based on the orthographic practice, McCollum & Kavitskaya (2018) suggest that this class of suffixes does not trigger harmony on following high vowels. Rounding harmony is orthographically represented elsewhere in the language, but not in this particular context. [^]
  6. Although (19e) is clearly a loan, (19c) is also a loan from Arabic that behaves like a native root, [xusus-ɯ] ‘answer-poss.3s.’ [^]
  7. We suspect directional evaluation (Anderson 1974; Kenstowicz & Kisseberth 1979) would require the composed rules in a mirror-image rule to be evaluated separately. [^]
  8. Tone is not marked in Ampofo & Rasin (2020). [^]

Competing interests

The authors have no competing interests to declare.

References

Allen, W. Sidney. 1951. Some prosodic aspects of retroflexion and aspiration in Sanskrit. Bulletin of the School of Oriental and African Studies, University of London 13(4). 939–946. DOI:  http://doi.org/10.1017/S0041977X00124152

Ampofo, Joana Serwaa & Rasin, Ezer. 2021. True self-counterfeeding vowel harmony in Akan serial verb constructions. In Proceedings of the 51st Annual Meeting of the North East Linguistics Society.

Anderson, Stephen R. 1974. The organization of phonology. San Diego, CA: Academic Press.

Andersen, Torben. 1999. Vowel harmony and vowel alternation in Mayak (Western Nilotic). Studies in African Linguistics 28(1). 1–30. DOI:  http://doi.org/10.32473/sal.v28i1.107377

Anttila, Arto. 1997. Deriving variation from grammar. In Hinskens, Frans & van Hout, Roeland & Wetzels, W. Leo (eds.), Variation, Change, and Phonological Theory, 35–68. Amsterdam: John Benjamins. DOI:  http://doi.org/10.1075/cilt.146.04ant

Archangeli, Diana & Pulleyblank, Douglas. 1994. Grounded phonology. Cambridge, MA: MIT Press.

Baković, Eric. 2000. Harmony, dominance, and control. New Brunswick, NJ: Rutgers University dissertation.

Balakaev, M.B. 1962. Sovremennij kazakhskij jazyk [Modern Kazakh language]. Alma-Ata: Nauka.

Bane, Max & Riggle, Jason. 2008. Three correlates of the typological frequency of quantity-insensitive stress systems. In Proceedings of the Tenth Meeting of ACL Special Interest Group on Computational Morphology and Phonology, 29–38. DOI:  http://doi.org/10.3115/1626324.1626330

Baski, Imre. 1986. A Crimean Turkic-Tatar glossary from the 17th century. Acta Orientalia Academiae Scientiarum Hungaricae 40(1). 107–172.

Bates, Douglas & Machler, Martin & Bolker, Ben & Walker, Steve. 2015. Fitting linear mixed-effects models using lme4. Journal of Statistical Software 67(1). 1–48. DOI:  http://doi.org/10.18637/jss.v067.i01

Bell-Berti, Fredericka & Harris, Katherine S. 1982. Temporal patterns of coarticulation: Lip rounding. The Journal of the Acoustical Society of America 71(2). 449–454. DOI:  http://doi.org/10.1121/1.387466

Berta, Árpád. 1998. West Kipchak Languages. In Johanson, Lars & Csató, Éva Ágnes (eds.), The Turkic Languages, 301–317. New York: Routledge.

Boersma, Paul & Weenink, David. 2015. Praat: doing phonetics by computer (Version 5.4.18).

Bowers, Dustin. 2019. Positional vs. sonority-driven stress in Gujarati: New experimental evidence. Phonological Data and Analysis 1(1). 1–28. DOI:  http://doi.org/10.3765/pda.v1art1.19

Casali, Roderic F. 2002. Nawuri ATR harmony in typological perspective. Journal of West African Languages 29(1). 3–43.

Casali, Roderic F. 2012. [+ATR] dominance in Akan. Journal of West African Languages 39(1). 33–59.

Cassimjee, Farida & Kisseberth, Charles. 1998. Optimal domains theory and Bantu tonology. In Hyman, Larry M. & Kisseberth, Charles (eds.), Theoretical aspects of Bantu tone, 265–314. Center for the Study of Language and Information.

Chandlee, Jane. 2021. What do we really mean by (non)iterativity? Presented at the North American Phonology Conference 11 (NaPhCxi).

Chomsky, Noam & Halle, Morris. 1968. The sound pattern of English. New York: Harper & Row.

Clements, George N. 1984. Principles of tone assignment in Kikuyu. In Clements, George N. & Goldsmith, John (eds.), Autosegmental studies in Bantu tone, 281–339. Foris Publications. DOI:  http://doi.org/10.1515/9783110864465

Coetzee, Andries. 2004. What it means to be a loser: Non-optimal candidates in Optimality Theory. University of Massachusetts, Amherst dissertation.

Coetzee, Andries W. & Pater, Joe. 2011. The Place of Variation in Phonological Theory. In Goldsmith, John A. & Riggle, Jason & Alan C. L. Yu (eds.), The handbook of phonological theory, Second Ed., 401–434. Malden, MA: Wiley-Blackwell. DOI:  http://doi.org/10.1002/9781444343069.ch13

Davis, Stuart. 1995. Emphasis spread in Arabic and grounded phonology. Linguistic Inquiry 26(3). 465–498.

de Lacy, Paul. 2014. Evaluating evidence for stress systems. In Van der Hulst, Harry (ed.), Word stress: Theoretical and typological issues, 149–193. Cambridge: Cambridge University Press. DOI:  http://doi.org/10.1017/CBO9781139600408.008

Dettweiler, Stephen H. 2000. Vowel harmony and neutral vowels in C’Lela. The Journal of West African Languages 28(1). 3–18.

Downing, Laura J. 2018. Is vowel harmony canonically (P)Word bound? An Africanist perspective on vowel harmony domains. Presented at the Generative Linguistics in the Old Word (GLOW) 41, Budapest.

Downing, Laura J. & Krämer, Martin. to appear. Phrasal vowel harmony. In Ritter, Nancy & Van der Hulst, Harry (eds.), Oxford handbook of vowel harmony. Oxford: Oxford University Press.

Hale, Mark & Reiss, Charles. 2008. The phonological enterprise. Oxford: Oxford University Press.

Hayes, Bruce & Tesar, Bruce & Zuraw, Kie 2011. OTSoft (Version 2.5). Retrieved from http://www.linguistics.ucla.edu/people/hayes/otsoft/

Hess, Susan. 1992. Assimilatory effects in a vowel harmony system-an acoustic analysis of advanced tongue root in Akan. Journal of Phonetics 20(4). 475–492. DOI:  http://doi.org/10.1016/S0095-4470(19)30651-5

Howard, Irwin. 1973. A directional theory of rule application. Indiana University Linguistics Club.

Hyman, Larry M. 1976. Phonologization. In Linguistic Studies Offered to Joseph Greenberg, Vol. 2, 407–418. Saratoga, CA: Anma Libri.

Hyman, Larry M. 2011. Tone: is it different. In Goldsmith, John A. & Riggle, Jason & Yu, Alan C. L. (eds.), The handbook of phonological theory, Second Ed., 197–239. Malden, MA: Wiley-Blackwell. DOI:  http://doi.org/10.1002/9781444343069.ch7

Hyman, Larry M. 2013. Enlarging the scope of phonologization. In Yu, Alan C. L. (ed.), Origins of sound change: Approaches to phonologization, 3–28. Oxford: Oxford University Press. DOI:  http://doi.org/10.1093/acprof:oso/9780199573745.003.0001

Itô, Junko & Mester, Armin & Padgett, Jaye. 1995. Licensing and underspecification in Optimality Theory. Linguistic Inquiry 26(4). 571–613.

Jensen, John T. & Stong-Jensen, Margaret. 1973. Ordering and directionality of iterative rules. Research on Language & Social Interaction 6(1–4). 66–90. DOI:  http://doi.org/10.1080/08351817309370329

Johnson, C. Douglas. 1972. Formal aspects of phonological description. The Hague: Mouton. DOI:  http://doi.org/10.1515/9783110876000

Jurgec, Peter. 2011. Feature Spreading 2.0: A unified theory of assimilation. Tromsø, Norway: University of Tromsø dissertation.

Kaisse, Ellen M. 2019. What kinds of processes are postlexical? In Hongming, Zhang & Youyong, Qian (eds.), Prosodic Studies: Challenges and Prospects, 227–251. New York: Routledge. DOI:  http://doi.org/10.4324/9781351212878-9

Kaplan, Aaron. 2008. Noniterativity is an emergent property of grammar. University of California, Santa Cruz dissertation.

Kaplan, Aaron. 2015. Maximal prominence and a theory of possible licensors. Natural Language & Linguistic Theory 33(4). 1235–1270. DOI:  http://doi.org/10.1007/s11049-014-9273-5

Kaun, Abigail. 1995. The typology of rounding harmony: An optimality theoretic approach. Los Angeles, CA: University of California, Los Angeles dissertation.

Kavitskaya, Darya. 2004. Syncope in Crimean Tatar. MIT Working Papers in Linguistics 46.

Kavitskaya, Darya. 2010. Crimean Tatar. Munich: Lincom Europa.

Kavitskaya, Darya. 2013. Segmental inventory and the evolution of harmony in Crimean Tatar. Turkic Languages 17(1). 86–114.

Kavitskaya, Darya & McCollum, Adam G. to appear. The rise and fall of rounding armony in Turkic. In Kavitskaya, Dary & Yu, Alan C. L. (eds.), The Life Cycle of Language: Past, Present, and Future. Oxford: Clarendon Press.

Kaye, Jonathan. 1982. Harmony processes in Vata. In Van der Hulst, Harry & Smith, Norval (eds.), The structure of phonological representations, Vol. 2, 385–452. Foris Publications. DOI:  http://doi.org/10.1515/9783112423325-011

Kenstowicz, Michael & Kisseberth, Charles. 1977. Topics in phonological theory. San Diego, CA: Academic Press.

Kenstowicz, Michael & Kisseberth, Charles. 1979. Generative phonology: Description and theory. San Diego, CA: Academic Press.

Key, Micheal & Bickmore, Lee. 2014. Headed tone spans: Binarity and minimal overlap. Southern African Linguistics and Applied Language Studies 32(1). 35–53. DOI:  http://doi.org/10.2989/16073614.2014.925218

Kiparsky, Paul. 1985. Some consequences of lexical phonology. Phonology 2(1). 85–138. DOI:  http://doi.org/10.1017/S0952675700000397

Kisseberth, Charles W. 2007. Tone (review). Language 83(3). 662–664. DOI:  http://doi.org/10.1353/lan.2007.0112

Kisseberth, Charles & Odden, David. 2003. Tone. In Nurse, Derek & Philippson, Gerard (eds.), The Bantu Languages, 59–70. New York: Routledge.

Kügler, Frank. 2015. Phonological phrasing and ATR vowel harmony in Akan. Phonology 32(1). 177–204. DOI:  http://doi.org/10.1017/S0952675715000081

Lahiri, Aditi. 2000. Hierarchical restructuring in the creation of verbal morphology in Bengali and Germanic: Evidence from phonology. In Lahiri, Aditi (ed.), Analogy, levelling, markedness: Principles of change in phonology and morphology, 71–123. Berlin: Mouton de Gruyter. DOI:  http://doi.org/10.1515/9783110808933

Legendre, Géraldine & Miyata, Yoshiro & Smolensky, Paul. 1990. Harmonic grammar: A formal multi-level connectionist theory of linguistic well-formedness: Theoretical foundations. University of Colorado.

Lehman, Blake. 2018. Tone-prominence interaction in Hän poster. Presented at the 2018 Annual Meeting on Phonology.

Lenth, Russell & Singmann, Henrik & Love, Jonathon. 2018. Emmeans: Estimated marginal means, aka least-squares means. R Package Version 1(1).

Lionnet, Florian. 2017. A theory of subfeatural representations: the case of rounding harmony in Laal. Phonology 34(3). 523–564. DOI:  http://doi.org/10.1017/S0952675717000276

Lobanov, Boris M. 1971. Classification of Russian vowels spoken by different speakers. Journal of the Acoustical Society of America 49(4B). 606–608. DOI:  http://doi.org/10.1121/1.1912396

Lombardi, Linda. 1999. Positional faithfulness and voicing assimilation in Optimality Theory. Natural Language & Linguistic Theory 17(2). 267–302. DOI:  http://doi.org/10.1023/A:1006182130229

Mahanta, Shakuntala. 2008. Directionality and locality in vowel harmony: With special reference to vowel harmony in Assamese. Utrecht: LOT.

Manker, Jonathan. 2014. Tone specification and the tone-bearing unit (TBU) in Hän Athabascan. Presented at the The Workshop on Structure and Constituency in Languages of the Americas 19.

McCarthy, John J. 1984. Theoretical consequences of Montañes vowel harmony. Linguistic Inquiry 15(2). 291–318.

McCollum, Adam G. 2015. Labial harmonic shift in Kazakh: Mapping the pathways and motivations for decay. In Jurgensen, Anna E. & Sande, Hannah & Lamoureux, Spencer & Baclawski, Kenny & Zerbe, Allison (eds.), The Proceedings of the 41st Annual Meeting of the Berkeley Linguistics Society, 329–352. DOI:  http://doi.org/10.20354/B4414110012

McCollum, Adam G. to appear. On how and why vowel harmony decays. In Ritter, Nancy & Van der Hulst, Harry (eds.), The Oxford Handbook of Vowel Harmony. Oxford: Oxford University Press.

McCollum, Adam G. & Kavitskaya, Darya. 2018. Non-iterative vowel harmony in Crimean Tatar. In Proceedings of the 35th West Coast Conference on Formal Linguistics, 259–268.

McPherson, Laura & Hayes, Bruce. 2016. Relating application frequency to morphological structure: the case of Tommo So vowel harmony. Phonology 33(1). 125–167. DOI:  http://doi.org/10.1017/S0952675716000051

Memetov, Ayder. 2012. Krymskotatarskij yazyk: fonetika [Crimean Tatar language: Phonetics]. Simferopol: Krymuchpedgiz.

Memetov, Ayder. 2013. Krymskotatarskij yazyk: istoriya izucheniya, leksikologiya, fonetika, morfologiya [Crimean Tatar language: History of study, lexicology, phonetics, morphology]. Simferopol: Krymuchpedgiz.

Menges, Karl H. 1947. Qaraqalpaq grammar. Morningside Heights, NY: King’s Cross Press. DOI:  http://doi.org/10.7312/meng92488

Mohanan, Karuvannur Puthanveettil. 1982. Lexical phonology. Cambridge, MA: Massachusetts Institute of Technology dissertation.

Myers, Scott. 1999. Tone association and f0 timing in Chichewa. Studies in African Linguistics 28(2). 215–239. DOI:  http://doi.org/10.32473/sal.v28i2.107375

Myers, Scott. 2003. F0 Timing in Kinyarwanda. Phonetica 60(2). 71–97. DOI:  http://doi.org/10.1159/000071448

Nevins, Andrew. 2010. Locality in vowel harmony. Cambridge, MA: MIT Press. DOI:  http://doi.org/10.7551/mitpress/9780262140973.001.0001

Obiri-Yeboah, Michael & Rose, Sharon. 2022. Vowel harmony and phonological phrasing in Gua. Natural Language & Linguistic Theory 40. 159–193. DOI:  http://doi.org/10.1007/s11049-021-09509-y

Odden, David. 1994. Adjacency parameters in phonology. Language 70(2). 289–330. DOI:  http://doi.org/10.2307/415830

Pearce, Mary. 2006. The interaction between metrical structure and tone in Kera. Phonology 23(2). 259–286. DOI:  http://doi.org/10.1017/S095267570600090X

Pearce, Mary. 2007. Iambicity in Kera. In Selected proceedings of the 37th Annual Conference on African Linguistics, 66–76. Cascadilla Proceedings Project.

Perkell, Joseph S. & Matthies, Melanie L. 1992. Temporal measures of anticipatory labial coarticulation for the vowel /u/: Within-and cross-subject variability. The Journal of the Acoustical Society of America 91(5). 2911–2925. DOI:  http://doi.org/10.1121/1.403778

Piggott, Glyne L. 1996. Implications of consonant nasalization for a theory of harmony. Canadian Journal of Linguistics/Revue Canadienne de Linguistique 41(2). 141–174. DOI:  http://doi.org/10.1017/S0008413100016303

Prince, Alan & Smolensky, Paul. 2004. Optimality Theory: Constraint interaction in generative grammar. Wiley-Blackwell. DOI:  http://doi.org/10.1002/9780470759400

R Core Team. 2017. R: A language and environment for statistical computing (Version 3.4.2). R foundation for statistical computing.

Radlov, Vasily V. 1896. Narechia Severnyx Tjurkskix plemen. Obrazcy narodnoj literatury: chastj vii [Dialects of the Northern Türkic tribes Samples of folk literature: Vol. vii]. Sankt Peterburg: Tipografia imperatorskoj akademii nauk.

Riggle, Jason. 2010. Sampling rankings. University of Chicago. Retrieved from http://roa.rutgers.edu/article/view/1105

Ringen, Catherine O. 1988. Transparency in Hungarian vowel harmony. Phonology 5(2). 327–342. DOI:  http://doi.org/10.1017/S0952675700002335

Ryan, Kevin. 2017. Attenuated spreading in Sanskrit retroflex harmony. Linguistic Inquiry 48(2). 299–340. DOI:  http://doi.org/10.1162/LING_a_00244

Samek-Lodovici, Vieri & Prince, Alan. 1999. Optima. University College London and Rutgers University. Retrieved from http://roa.rutgers.edu/article/view/373

Sevortjan, Ervand V. 1966. Krymsko-tatarskij yazyk [Crimean Tatar Language]. In Vinogradov, Viktor V. (ed.), Jazyki Narodov SSSR: Tyurkskie yazyki [Languages of the peoples of the USSR: Turkic languages], 234–259. Leningrad: Nauka.

Shih, Shu-hao. 2018. On the existence of sonority-driven stress in Gujarati. Phonology 35(2). 327–364. DOI:  http://doi.org/10.1017/S0952675718000064

Smolensky, Paul. 2006. Optimality in phonology II: Harmonic completeness, local constraint conjunction, and feature domain markedness. In Smolensky, Paul & Legendre, Geraldine (eds.), The harmonic mind: From neural computation to optimality-theoretic grammar, Vol. 2, 27–160. Cambridge, MA: MIT Press.

Tabain, Marija. 2003. Effects of prosodic boundary on /aC/ sequences: acoustic results. Journal of the Acoustical Society of America 113(1). 516–531. DOI:  http://doi.org/10.1121/1.1523390

Topintzi, Nina & Van Oostendorp, Marc. 2009. Palatalization and centralization in Samothraki Greek. Studies in Greek Linguistics 29. 385–399.

Vago, Robert M. 1988. Underspecification in the height harmony system of Pasiego. Phonology 5(2). 343–362. DOI:  http://doi.org/10.1017/S0952675700002347

Van Oostendorp, Marc & Revithiadou, Anthi. 2005. Quasi-opacity and headed spans in Silly and Megisti Greek. In 13th Manchester Phonology Meeting, University of Manchester, Manchester. Retrieved from http://www.vanoostendorp.nl/pdf/mfm2005.pdf

Van Zanten, Ellen & Goedemans, Rob & Pacilly, Jos. 2003. The status of word stress in Indonesian. Amsterdam Studies in the Theory and History of Linguistic Science Series 4. 151–178. DOI:  http://doi.org/10.1075/cilt.234.11zan

Vaux, Bert. 2008. Why the phonological component must be serial and rule-based. In Vaux, Bert & Nevins, Andrew (eds.), Rules, constraints, and phonological phenomena, 20–60. Oxford: Oxford University Press. DOI:  http://doi.org/10.1093/acprof:oso/9780199226511.003.0002

Vaux, Bert & Myler, Neil. 2017. Issues and prospects in rule-based phonology. In Hannahs, S. J. & Bosch, Anna R. K. The Routledge handbook of phonological theory, 167–196. Routledge. DOI:  http://doi.org/10.4324/9781315675428-7

Vayra, Mario & Fowler, Carol A. 1992. Declination of supralaryngeal gestures in spoken Italian. Phonetica 49(1). 48–60. DOI:  http://doi.org/10.1159/000261902

Walker, Rachel. 2005. Weak triggers in vowel harmony. Natural Language & Linguistic Theory 23(4). 917. DOI:  http://doi.org/10.1007/s11049-004-4562-z

Walker, Rachel. 2011. Vowel patterns in language. Cambridge: Cambridge University Press.

Wang, Xiaomei & Lin, Yen-Hwei. 2017. No more conflicting directionality: Metrical conditions on Tianjin Chinese trisyllabic tone sandhi. In Proceedings of the Annual Meetings on Phonology. DOI:  http://doi.org/10.3765/amp.v4i0.3993

Whitney, William Dwight. 1879. Sanskrit grammar: Including both the classical language, and the older dialects, of Veda and Brahmana. Leipzig: Breitkopf and Hartel.

Xu, Yi. 2001. Fundamental frequency peak delay in Mandarin. Phonetica 58(1–2). 26–52. DOI:  http://doi.org/10.1159/000028487

Yip, Moira. 2002. Tone. Cambridge: Cambridge University Press.

Zaiceva, Maria I. 1981. Grammatika Vepsskogo yazyka: Fonetika i morfologiya [Grammar of the Veps Language: Phonetics and Morphology]. Nauka.