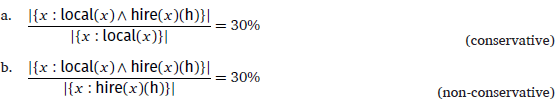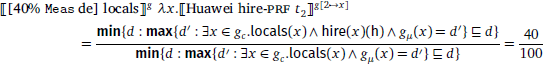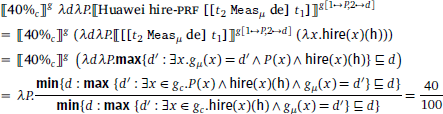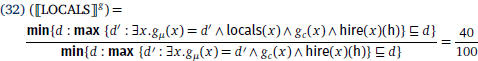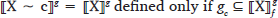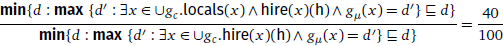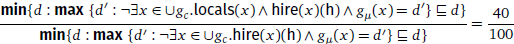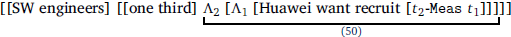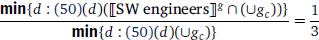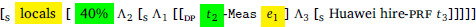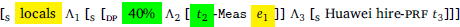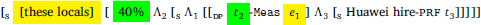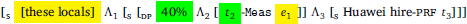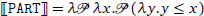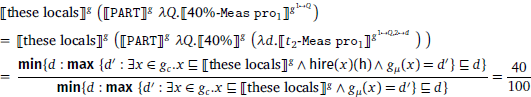1 Introduction

There are two kinds of measurement in natural language: absolute measurement, expressible by phrases such as three liters and five inches, and relative measurement, expressible by proportional number expressions, such as 20% and two thirds. Absolute measurement is about a single measure, as shown in (1), where the numeral phrase 300 locals refers to the number of locals hired by Huawei. By contrast, relative measurement is about the relation between two measures, as shown in (2), where the relative measure phrase (RM phrase, for short) 30% of the locals refers to the proportion of Huawei’s local employees in the local population in a given context.

    1. (1)
    1. Huawei hired 300 locals.
    1. (2)
    1. Huawei hired 30% of the locals.

Most studies on measurement focus on absolute measurement, leaving relative measurement a relatively under-explored research topic. However, a series of recent work by Ahn, Sauerland and Pasternak have revealed that relative measurement has interesting semantic properties that warrant further investigation (Sauerland 2014; Ahn & Sauerland 2015a; b; 2017; Pasternak & Sauerland to appear; a.o.).

One of their observations is that in many languages relative measurement may be expressed by two constructions of relative measurement (RM construction, for short). For example, besides (2), where the RM phrase is a kind of partitive phrase, the following sentence is also acceptable in English.

    1. (3)
    1. Huawei hired 30% locals.

The RM phrase in (3) not only differs in form from the one in (2), but it also gives rise to a different meaning. Specifically, the RM phrase in (3) refers to the locals hired by Huawei relative, not to the local population, but to the total hires at Huawei. The respective readings can be translated as (4a) and (4b). The representations in (4) follow the standard theory of generalized quantifiers (Barwise & Cooper 1981): relative measurement is formally treated as quantification over objects, expressing the proportion of one set of objects in the other set. The difference between (4a) and (4b) is that they take different denominators.

    1. (4)

Given the conservativity of generalized quantifiers, as in (5), proposed by Keenan & Stavi (1986) (cf. Barwise & Cooper 1981), the representation in (4a) is conservative, but the one in (4b) is non-conservative.1

    1. (5)
    1. For DP quantification D(A)(B), D is a relation between sets denoted by the quantificational determiner, A is the set denoted by the NP complement and B is the set denoted by the rest of the sentence. D is conservative iff D(A)(B) is equivalent to D(A)(A∩B).

The studies conducted by Ahn and Sauerland argue that the reading of (3) does not falsify conservativity. Instead, the semantic difference between (2) and (3) has structural origins: (2) and (3) have different syntactic structures that underlie the distinct readings (see also Pasternak & Sauerland to appear). Nonetheless, for terminological consistency with previous studies, I still refer to (4a) as a conservative reading, and (4b) as a non-conservative reading.

Despite these structural differences, an RM phrase has as its core a quantifier semantics. As has been noticed for decades, different quantifiers exhibit different scope behaviors (Ioup 1975; Liu 1990; Beghelli & Stowell 1997; Takahashi 2006; Barker 2021; a.o.). A natural question then arises as to how an RM phrase interacts with other scope-bearing elements. However, as far as I know, this issue has not received much attention. In light of this, this paper draws on RM phrases in Mandarin to shed light on the scope of RM phrases.

Unlike RM constructions in English (as well as German, Korean and French), both the conservative reading and the non-conservative reading can be expressed by the same construction in Mandarin, as shown in (6) and (7).2 In Mandarin, a percentage number expression consists of two items, i.e., bǎifēnzhī ‘percent’ and a simple number expression.3

    1. (6)
    1. Huáwéi
    2. Huawei
    1. gù-le
    2. hire-prf
    1. bǎifēnzhī
    2. percent
    1. sānshí
    2. 30
    1. de
    2. lnk
    1. běndì-rén.
    2. local-people
    1. ‘Huawei has hired 30% of the locals.’                                                      (conservative)
    1. (7)
    1. Huáwéi
    2. Huawei
    1. gù-le
    2. hire-prf
    1. bǎifēnzhī
    2. percent
    1. sānshí
    2. 30
    1. de
    2. lnk
    1. BĚNDÌ-RÉN.
    2. local-people
    1. ‘Huawei has hired 30% LOCALS and 70% NON-LOCALS.’               (non-conservative)

According to Ahn & Sauerland (2017), the only distinction between these examples is that the non-conservative reading requires contrastive focus on the NP complement. The ‘NP-focusing’ requirement is supported by the fact that a non-conservative reading becomes salient when another RM phrase exists that spells out the contrastive set (e.g. běndì-rén ‘locals’ vs. wàidì-rén ‘non-locals’), as shown in (8). In the paper, focused expressions are capitalized.

    1. (8)
    1. Huáwéi
    2. Huawei
    1. gù-le
    2. hire-prf
    1. 30%
    2. 30%
    1. de
    2. lnk
    1. BĚNDÌ-RÉN,
    2. local-people
    1. 70%
    2. 70%
    1. de
    2. lnk
    1. WÀIDÌ-RÉN.
    2. non-local-people
    1. ‘Huawei has hired 30% LOCALS and 70% NON-LOCALS.’                  (non-conservative)

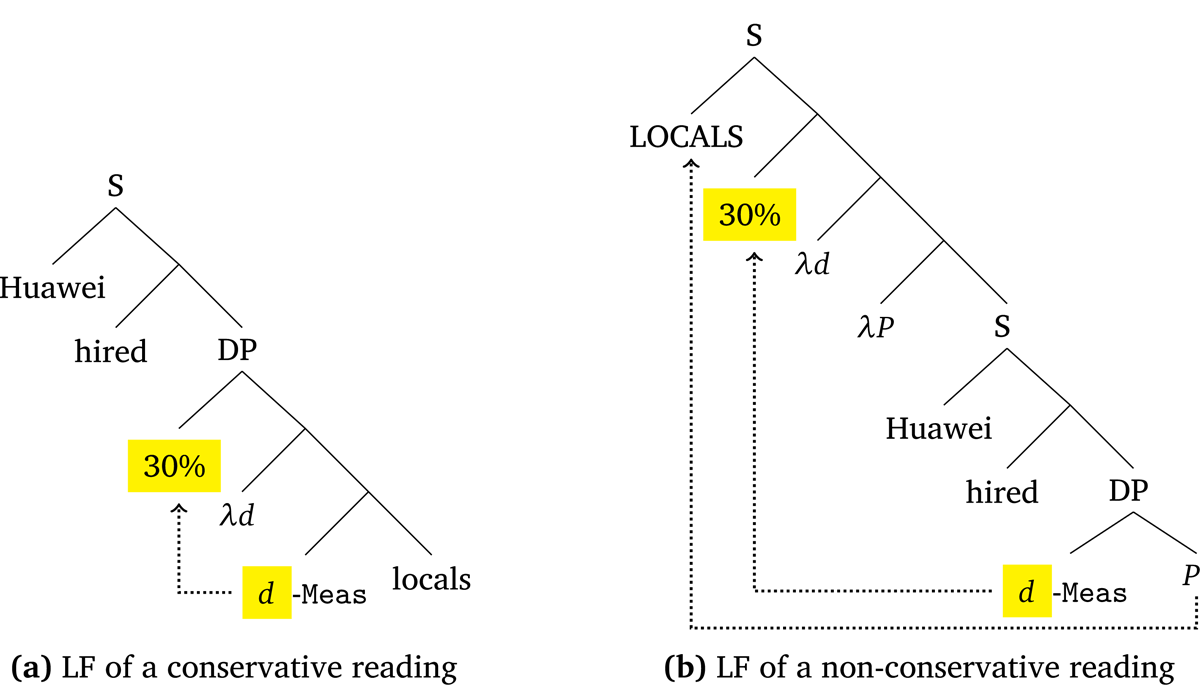
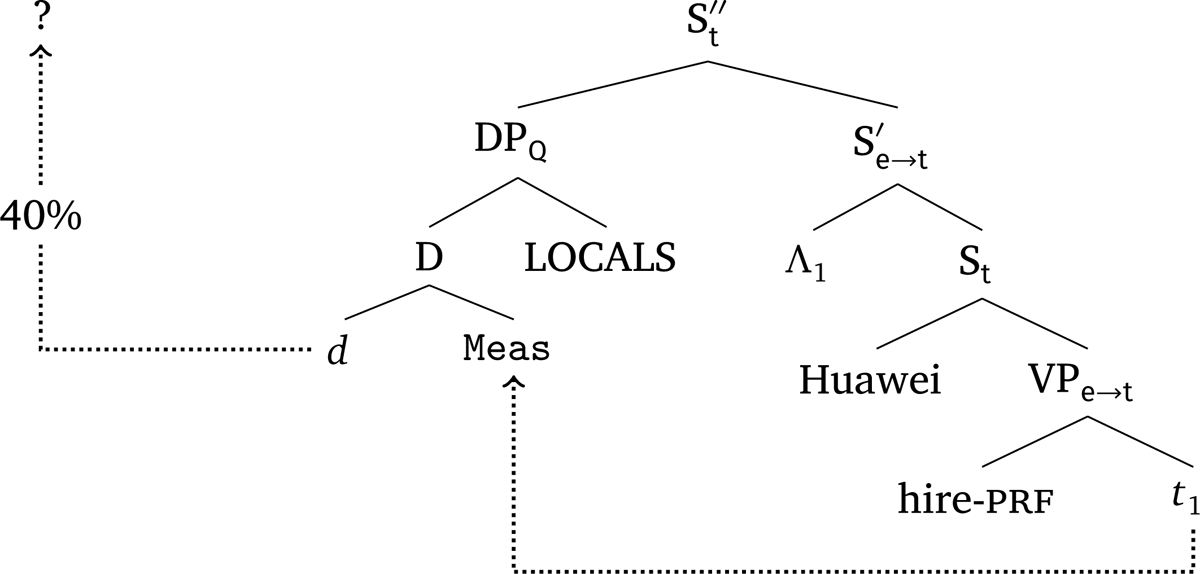
Empirically, it is discovered in this paper that an RM phrase exhibits distinct scope patterns when it participates in different interpretations: (a) an RM phrase participating in a conservative reading (called a ‘conservative’ RM phrase) can scope over a scope-bearing element c-commanding it; (b) an RM phrase participating in a non-conservative reading (called a ‘non-conservative’ RM phrase) cannot. I propose that an RM phrase should be decomposed into two parts—a proportional number expression, such as 30%, and a measure phrase, which is projected by a null functional head Meas. The proportional number expression denotes a degree quantifier and scopes at different positions in the conservative and the non-conversative reading. Specifically, in a ‘conservative’ RM phrase, the proportional number expression scopes at the edge of the RM phrase, as depicted in Figure 1a; whereas, in a ‘non-conservative’ RM phrase, the proportional number expression targets a scopal position created by the covert focus movement of the NP complement of the RM phrase, as depicted in Figure 1b.

Figure 1
Figure 1

RM phrases: two ways of scope taking.

This proposal is reminiscent of the scopal analysis of superlatives and comparatives (Szabolcsi 1986; Heim 2000; Takahashi 2006; Hackl 2000; 2009; Tomaszewicz 2015; Bumford 2017; a.o.). As is well known, the sentence in (9) as well as the Mandarin counterpart (10) have two readings. One reading indicates that Mary climbed Mont Everest, while the other one says that, among a set of contextually given people, the mountain that Mary climbed is the highest.

    1. (9)
    1. Mary climbed the highest mountain.
    1. (10)
    1. Mǎlì
    2. Mary
    1. pá-le
    2. climb-prf
    1. zùi
    2. -est
    1. gāo
    2. high
    1. de
    2. lnk
    1. shān.
    2. mountain
    1. ‘Mary climbed the highest mountain.’

The superlative morpheme -est (zùi in Mandarin) is treated as a degree quantifier. The first reading is generated by scoping -est at the edge of the superlative NP, as what we see in Figure 1a; while the second reading is generated by scoping -est at the outside of the superlative NP, as we see in Figure 1b.

In short, both proportional number expressions and superlative expressions may either take DP-internal scope or DP-external scope. When taking DP-external scope, a degree quantifier may scope above another scope-bearing element (SBE), as schematized in (11).

    1. (11)
    1. [… [degree quantifier] λd.[… SBE … d …]]

It has been observed that the scope pattern illustrated in (11) is severely constrained (Kennedy 1997; Heim 2000; Hackl 2000; a.o.). Following the spirit of Takahashi (2006), I argue that the inability of a ‘non-conservative’ RM phrase to take scope over other scope-bearing elements stems from the general restricted scope-taking potential of degree quantifiers. For concreteness, building on the theory of degree pluralities proposed in Dotlačil & Nouwen (2016), I show that the degree quantifier denoted by a proportional number expression cannot scope across another scope-bearing element. Otherwise, the resulting LF leads to undefinedness.

Analyzing proportional number expressions as degree quantifiers is close to Pasternak & Sauerland’s (to appear) recent study of German RM constructions. Especially, they also propose that the proportional number expression in a ‘non-conservative’ RM phrase denotes a degree quantifier and takes DP-external scope. However, my analysis diverges from theirs in several areas. A brief comparison is offered in Appendix.

This paper is organized as follows. Section 2 presents the scope facts exhibited by RM phrases, which constitute the primary empirical contribution of the paper. Section 3 proposes a decompositional analysis for RM phrases and demonstrates how the proposed analysis accounts for the scope facts. Section 4 extends the decompositional analysis to two structural issues. Section 5 concludes. Four appendices are included in a supplementary file. Appendix A presents a structured survey clarifying the non-conservative reading. Appendix B stores more data about scope possibilities of RM phrases. Appendix C discusses an extra scope interpretation observed for RM phrases. In the end, Appendix D offers a brief comparison with Pasternak & Sauerland (to appear).

2 Scope of RM phrases

Although RM phrases are treated as quantifiers in previous studies, it remains unclear how they interact with other scope bearing elements. This section draws Mandarin data to shed light on the scopability of RM phrases: RM phrases do not show consistent scope taking potentials. Whether or not they may take scope over another scope-bearing elements depends on whether they participate in a conservative reading or a non-conservative reading. Specifically, a ‘conservative’ RM phrase can scope over another scope bearing element (e.g., negation, quantificational DPs, intensional operators); whereas, a ‘non-conservative’ RM phrase always takes narrow scope.4

Negation When an RM construction has a conservative reading, the RM phrase can scope above or below negation, as shown in (12). If negation scopes over the RM phrase, (12) is true if the locals hired by Huawei made up less than 70% of the local population. On the other hand, if the RM phrase takes scope over negation, (12) is true in case there were some locals that Huawei did not hire and they made up (at least) 70% of the local population.

    1. (12)
    1. Huáwéi
    2. Huawei
    1. méiyǒu
    2. not
    1. gù
    2. hire
    1. 70%
    2. 70%
    1. de
    2. de
    1. běndì-rén.
    2. local-people
    1.  
    1. a.
    1. Conservative: not > 70% locals
    2. ‘It is not the case that Huawei hired 70% of the locals.’
    1.  
    1. b.
    1. Conservative: 70% locals > not
    2. ‘70% of the locals were such that Huawei didn’t hire them.’

By contrast, if an RM construction has a non-conservative reading, the RM phrase must take narrow scope relative to negation c-commanding it in the surface structure. Consider (13). This sentence only has one well-formed reading, i.e., (13a). It is true only if the locals hired by Huawei made up less than 70% of all the employees at Huawei.

    1. (13)
    1. Huáwéi
    2. Huawei
    1. méiyǒu
    2. not
    1. gù
    2. hire
    1. 70%
    2. 70%
    1. de
    2. de
    1. BĚNDÌ-RÉN.
    2. local-people
    1.  
    1. a.
    1.   Non-conservative: not > 70% locals:
    2.   ‘It’s not the case that 70% of Huawei’s employees were locals.’
    1.  
    1. b.
    1. #Non-conservative: 70% locals > not
    2.   ‘70% of the people that Huawei didn’t hire were locals.’

Regarding scope taking, an RM phrase behaves differently in a conservative reading and a non-conservative reading.

Intensional operators In addition to negation, ‘conservative’ RM phrases and ‘non-conservative’ RM phrases also exhibit distinct scopal possibilities in intensional contexts. Let us begin with ‘conservative’ RM phrases. Consider (14). This sentence can felicitously describe a recruitment plan of Huawei’s. It is judged true if the recruitment plan requires the target ratio of recruitment to be 1:3.

    1. (14)
    1. Huáwéi
    2. Huawei
    1. xiǎng
    2. want
    1. zhāo
    2. recruit
    1. sānfēnzhīyī
    2. one.third
    1. de
    2. lnk
    1. qiúzhízhě.
    2. candidates
    1. ‘Huawei wants to recruit one third of the candidates.’

In this situation, there are no particular candidates who are desired to be recruited. Under this interpretation, (14) receives a de dicto reading, which can be paraphrased as: for all worlds w compatible with Huawei’s desire in the actual world, it recruits one third of the candidates in w. In order to generate this reading, the RM phrase scopes below the intensional verb want.

The RM phrase can also scope above want, generating a de re reading. As in (15), this reading becomes prominent when the speaker has interviewed all candidates and considers some of them more suitable and desired.5

    1. (15)
    1. Huáwéi
    2. Huawei
    1. xiǎng
    2. want
    1. zhāo
    2. recruit
    1. sānfēnzhīyī
    2. one.third
    1. de
    2. lnk
    1. qiúzhízhě.
    2. candidates
    1. Zhè-xiē
    2. this-cl
    1. rén
    2. people
    1. dōu
    2. dou
    1. yǒu
    2. have
    1. hěn
    2. very
    1. fēngfù
    2. rich
    1. de
    2. lnk
    1. biānchéng
    2. programming
    1. jīngyàn.
    2. experiences
    1. ‘Huawei wants to recruit one third of the candidates. These peoople all have rich experiences of programming.’

Here Huawei would like to recruit some specific group of candidates, who are referred to by the demonstrative in the continuation. This is a typical de re reading and can be paraphrased as: one third of the candidates in the actual world are the ones such that Huawei desires to recruit them. In order to generate this reading, the RM phrase scopes above the intensional verb and is evaluated in the actual world.

Then, let us move on to ‘non-conservative’ RM phrases. Consider (16), which can be uttered when a recruitment plan was just made. At this moment, it is not known how many people will apply, and no particular software engineers are expected to get the jobs.

    1. (16)
    1. Huáwéi
    2. Huawei
    1. xiǎng
    2. want
    1. zhāo
    2. recruit
    1. sānfēnzhīyī
    2. one.third
    1. de
    2. lnk
    1. RUǍNJIÀN
    2. software
    1. gōngchéngshī.
    2. engineers
    1. ‘Huawei wants to recruit one third SOFTWARE engineers.’

(16) has a typical de dicto reading, which can be understood as: for all worlds w compatible with Huawei’s desire in the actual word, one third of the engineers recruited by Huawei are software engineers in w. This reading can result from interpreting the RM phrase within the scope of the intensional verb.

By contrast, de re readings are not available for ‘non-conservative’ RM phrase. Let’s consider such a scenario: there are 300 people that Huawei wants to recruit; among these people, 100 are software engineers, and the other 200 hardware engineers. Under this scenario, (17) does not receive a non-conservative interpretation. This is supported by the fact that the conservative reading, rather than the conservative reading, is preferred when the RM phrases are referred to by the demonstrative expression in the continuation.

    1. (17)
    1. Huáwéi
    2. Huawei
    1. xiǎng
    2. want
    1. zhāo
    2. recruit
    1. sānfēnzhīyī
    2. one.third
    1. de
    2. lnk
    1. RUǍNJIÀN
    2. software
    1. gōngchéngshī,
    2. engineers
    1. sānfēnzhīèr
    2. two.thirds
    1. de
    2. lnk
    1. YÌNGJIÀN
    2. hardware
    1. gōngchéngshī.
    2. engineers
    1. Zhè-xiē
    2. this-cl
    1. rén
    2. people
    1. dōu
    2. dou
    1. yǒu
    2. have
    1. hěn
    2. very
    1. fēngfù
    2. rich
    1. de
    2. lnk
    1. gōngzuò
    2. working
    1. jīngyàn.
    2. experiences
    1.  
    1. a.
    1. #‘Huawei wants to recruit one third SOFTWARE engineers and two thirds HARDWARE engineers. These people all have rich working experiences.’
    1.  
    1. b.
    1.   ‘Huawei wants to recruit one third of the software engineers and two thirds of the hardware engineers. These people all have rich working experiences.’

In this case, it is apparent that Huawei has a specific list of people to recruit. If the non-conservative reading is allowed in (17), the RM phrases would refer to two specific sets of engineers, which serve as the antecedent of the demonstrative expression, and should scope above the intensional verb. However, the infelicity of the non-conservative reading in this example implies that the RM phrase cannot take wide scope.6

The same pattern are also observed for the scope interaction of RM phrases and other kinds of intensional operators, such as modals. See Appendix B in the supplement file for the details.

Quantificational DPs The scope interaction of an RM phrase and a quantificational DP is not exactly the same as what we have observed. Unlike the interaction with negation or intensional verbs, an RM phrase consistently does not take inverse scope relative to a quantificational DP c-commanding it. Let’s first consider RM constructions with conservative readings. For example, (18) has an acceptable reading derived by scoping the RM phrase under the boldfaced exactly-DP.

    1. (18)
    1. Zhěnghǎo
    2. exactly
    1. yǒu
    2. have
    1. liǎng-gè
    2. two-cl
    1. xuéshēng
    2. students
    1. dú-le
    2. read-prf
    1. sānfēnzhīyī
    2. one.third
    1. de
    2. lnk
    1. xiǎoshūo.
    2. novels
    1.  
    1. a.
    1.    Conservative: exactly two students > one third novels
    2.    ‘There are exactly two students such that each of them read one third of the novels.’
    1.  
    1. b.
    1. ??Conservative: one third novels > exactly two students
    2.     ‘One third of the novels are the ones read by exactly two students.’

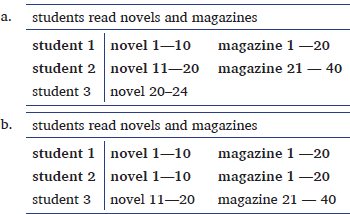
Given a context with 30 novels, i.e., novel 1, novel 2, … novel 30, the sentence is true in the scenario described in (19a), where only two students read 10 novels out of 30, but false in the scenario described by (19b), where each student read one third of the novels.

    1. (19)

If the RM phrase could take scope over the exact-DP, generating the reading in (18b), (18) would be judged true against (19b). In this scenario, the specific ten novels, novel 1–10, were read by exactly two students and made up one third of the novels. Since (18) is not true in this scenario, it indicates that the RM phrase cannot take inverse scope.

Turning to RM constructions with a non-conservative reading, we observe the same scope freezing effect. For example, in (20), which has a non-conservative reading, the RM phrase can only scope below the exactly-DP.

    1. (20)
    1. Zhěnghǎo
    2. exactly
    1. yǒu
    2. have
    1. liǎng-gè
    2. two-cl
    1. xuéshēng
    2. students
    1. dú-le
    2. read-prf
    1. sānfēnzhīyī
    2. one.third
    1. de
    2. lnk
    1. XIǍOSHŪO
    2. novels
    1. (sānfēnzhīèr
    2. two.thirds
    1. de
    2. lnk
    1. ZÁZHÌ).
    2. magazines
    1.  
    1. a.
    1.   Non-conservative: exactly two students > one third novels
    2.   ‘There are exactly two students such that they each read one third NOVELS (and two thirds MAGAZINES).’
    1.  
    1. b.
    1. #Non-conservative: one third novels > exactly two students
    2.    ‘One third of the books that exactly two students read were NOVELS. (Two thirds of the books that exactly two students read were MAGAZINES.)’

This sentence is judged true against the scenario in (21a). In this case, exactly two of the students read 10 novels and 20 magazines. So, the novels read by the two students made up one third of all books that they read. This shows that the reading in (20a) is attested.

    1. (21)

By contrast, the reading in (20b) is not available. If (20) had this reading, it would be true in scenario (21b). In this case, novel 1—10 and magazine 1—20 are the books that exactly two students read, and one third of the books are novels. This scenario verifies the reading in (20b), despite that student 3 also read 10 novels and 20 magazines. However, the sentence in (20) is not judged true in this scenario.

According to more investigations, the scope freezing effect is consistently observed in RM constructions with non-conservative readings and with conservative readings that contain other kinds of quantificational DPs. The relevant data are also listed in Appendix B in the supplementary file.

Summary We have examined the scope interactions of RM phrases and other scope bearing elements in both readings of RM constructions. The results are summarized below (RMP = RM phrase; INO = intensional operator; QDP = quantificational DP).

Table 1

Scope interactions of RM phrases and other scope bearing elements.

  conservative non-conservative
{NEG, RMP} NEG >/< RMP NEG > RMP
{INO, RMP} INO >/< RMP INO > RMP
{QDP, RMP} QDP > RMP QDP > RMP

The scope facts above lead us to draw the following descriptive generalization:

    1. (22)
    1. The scope generalization of RM phrases
    2. A ‘conservative’ RM phrase can take wide scope over another scope-bearing element; whereas, a ‘non-conservative’ RM phrase is consistently confined to take narrow scope.

This paper aims to present a new analysis of relative measurement, which not only compositionally derives the ambiguity between the conservative and non-conservative readings, but also provides a principled account for the scope generalization of RM phrases.

3 Proportional number expressions take scope

The core of my proposal is that proportional number expressions, such as 40 percent and one third, are degree quantifiers taking scope over generalized quantifiers (type Q := (e → t) → t). As a consequence, a proportional number expression must undergo QR at LF to resolve type mismatch. There are two possible scope positions it may target. First, it may scope at the edge of the RM phrase hosting it, which is a generalized quantifier over entities, and returns a generalized quantifier over entities. This scope taking leads to a conservative reading. Alternatively, it may scope beyond the RM phrase when the NP complement of the RM phrase bears focus. In this case, the scope of the proportional number expression depends on covert focus movement of the NP complement. That is, the focused NP covertly adjoins to a constituent of type t, creating a target position for the scope taking of the proportional number expression. As a result, a non-conservative reading is generated.

The availability of different scope possibilities for a proportional number expression leads to the natural expectation that it can scopally interact with other scope-bearing elements. However, as observed in the previous section, ‘non-conservative’ RM phrases have more restricted scope properties—they seem to only take narrow scope.

I argue that the narrow scope restriction is, in fact, not surprising given what we know about the scope properties of degree quantifiers. Previous studies have already observed that degree quantifiers have difficulty taking scope over other scope-bearing elements. The scope restrictions of ‘non-conservative’ RM phrases simply follow from these restrictions.

To account for the scopal restrictions of RM phrases along the lines of degree constructions, I borrow the notion of degree plurality from Dotlačil & Nouwen (2016). According to these authors, a degree plurality has difficulty being operated on by many sentential operators. For this reason, when the degree component in an RM phrase takes scope over another scope-bearing element, it leads to undefinedness, which in turn prohibits an RM phrase from taking wide scope (Takahashi 2006).

3.1 Background: degree plurality

The formal analysis that I propose partially relies on an assumption that the ontology and semantic mechanism designated for plurality of individuals should be extended to degrees, which is suggested by Heim (2006), Beck (2010) and Hsieh (2017). Among these studies, Dotlačil & Nouwen (2016) explicitly propose that the domain of degrees includes atomic degrees and their sums, i.e., non-atomic degrees. For concreteness, I assume with Schwarzschild (1996) that pluralities are modeled as sets: atomic degrees are singleton sets (type dat), while non-atomic degrees non-singleton sets. Any two atomic degrees like d and d′ can form a sum of them via summation construed as set union (d ⊔ d′ := d ∪ d′). The part-whole relation is characterized in terms of the subset relation: d ⊑ d′ := d ⊆ d′. So, like the domain of entities, the domain of degrees is closed by sum.

Although the domain of degrees includes atomic and non-atomic degrees, many degree operations are not defined for non-atomic degrees. For example, the scalar relation < of degrees makes sense only if degrees are atomic.7 Similarly, the division of one degree d from another one d′, i.e., should also be defined on atomic degrees.8

3.2 Deriving conservative readings

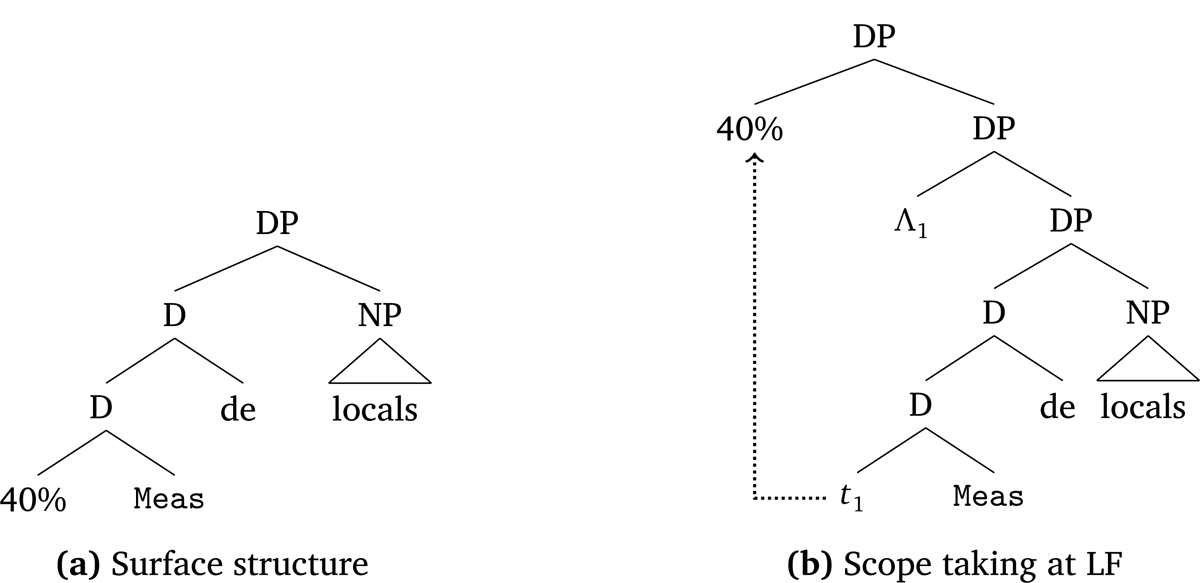
It has been widely assumed that a quantity expression can be decomposed into a degree quantifier and a counting quantifier (Hackl 2000; Takahashi 2006; Kennedy 2015; a.o.). In keeping with this line of research, I propose the structure exemplified in Figure 2a for RM phrases. A proportional number expression is adjoined to a phonologically null but semantically contentful functional element Meas. This forms a complex determiner head, which hosts the morpheme de and selects an NP as complement.9

Figure 2
Figure 2

RM phrases: surface structure and LF.

The main claim of this paper is that a proportional number expression is a degree quantifier taking scope over a generalized quantifier. Specifically, the proportional number expression 40% has the simplified denotation in (23) (to be revised to include intensionality in Section 3.4.2). It is of type (d → Q) → Q, which has the general type structure of scope taking expressions (Barker 2007). This type dictates that a proportional number expression can scope over a constituent of type Q and produce as a result another constituent of type Q. Given the fact that generalized quantifiers are usually denoted by DPs in natural language, proportional number expressions should be raised via QR at LF and adjoin to the edge of DP, as shown in Figure 2b.10

    1. (23)
    1. Definition of proportional number expressions (to be revised)

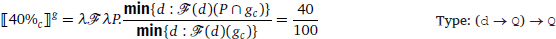
The building blocks of this definition is elaborated as follows. is a variable over objects of type d → Q, a type of a function from degrees to quantifier meanings. min is a minimality operator that operates on pluralities. It maps a set of degrees (including atomic and non-atomic ones) to the unique minimum of the set (the most informative member in the set). The concrete definition is given in (24).

    1. (24)
    1. min := λDdιd.d ∈ Dd ∧ ¬∃d′.d′ ∈ Dd ∧ d′ ⊏ d                                            Type: (d → t) → d

Moreover, c is a variable of type e → t, i.e., a contextually given set containing entities under discussion. Its value is yielded by assignments and written as gc. It is a context restriction of quantification (Westerstahl 1985, von Fintel 1994). Thus, the percentage is calculated based on two numbers, one relating to the context set gc and the other relating to the set P ∩ gc.

In Figure 2a, the head of the RM phrase is the covert functional item Meas. Cross-linguistically, Meas, or other corresponding items, has been argued to be an important component of a quantity expression (Kayne 2005; Solt 2015; Pasternak & Sauerland to appear; a.o.). Its main contribution is to specify what kind of measurement yields the relevant quantity. On the basis of the theory of degree pluralities, I assume that Meas, defined as in (25), denotes a degree-related quantificational determiner mapping degrees to relations of properties.

    1. (13)
    1. ⟦Measμ⟧g = λdλQλP.max{d′ : ∃x.Q(x) ∧ P(x) ∧ gμ(x) = d′} ⊑ d              Type: d → (e → t) → Q

The interpretations of Meas is relative to any assignment of values to variables. μ is a contextual variable ranging over measure functions of type of e → d. Specifically, the assignment g assigns a value to the variable μ, i.e., gμ. Potential values for μ are various extensive measure functions, such as weight, volume, cardinality and distance, but not intensive ones like temperature or speed (see also Solt 2015; Wellwood 2015; Ahn & Sauerland 2017; Pasternak & Sauerland to appear). In addition, Meas introduces some entities x via existential quantification and gμ relates the entities to the degrees. Then, Meas collects all the degrees into a set, maps the set to the maximum via the operator max, defined in (26), and generates a set of all degrees that have the maximum as an atomic part.11

    1. (26)
    1. max := λDdatιd.d ∈ Ddat ∧ ¬∃d′.d′ ∈ Ddat ∧ d′ ⩾ d                    Type: (d → t) → d

In Chinese Linguistics, the grammatical status of de is a subject of debate. A comprehensive discussion of de is beyond the scope of the paper. So, the present analysis does not dive into de’s status but simply assume that it denotes an identity function that maps any object to itself.

Now, we are in the position to show how these pieces are combined to generate the denotation of an RM phrase. Returning to Figure 2a, the proportional number expression 40% cannot combine with Meas due to type mismatch. This motivates QR of 40%, which adjoins 40% to the DP and leaves a number trace of type d, as illustrated in Figure 2b. Within the scope of 40%, DP denotes an existential generalized quantifier. The result of the compositional process, which I leave for readers to work out, is given in (27). In this case, the contextually-determined measure function is cardinality, i.e., the function that takes a (plural) entity and returns the number of atomic entities that it is composed.

    1. (27)
    1. ⟦DP⟧g = λP.max{d′ : ∃x.locals(x) ∧ P(x) ∧ gμ(x) = d′} ⊑ g1                                            Type: Q

Abstracting the value assigning to the trace via Λ-abstraction leads to a function mapping numbers to quantifiers, which serves as the scope argument of 40%. As a result, the whole RM phrase denotes a quantifier of type Q, as shown in (28).

    1. (28)

As a quantifier, the RM phrase undergoes QR at LF when we derive the meaning of the RM construction in (29). The derivation is demonstrated in (30). The Λ-abstraction creates a predicate of type e → t, i.e., λx.hire(x)(h). Feeding it to the meaning of the RM phrase in (28) generates the truth condition of (29).

    1. (29)
    1. Huáwéi
    2. Huawei
    1. gù-le
    2. hire-prf
    1. 40%
    2. 30%
    1. de
    2. lnk
    1. běndì-rén.
    2. local-people
    1. ‘Huawei has hired 30% of the locals.’                    (conservative)
    1. (30)

(30) expresses the equation of two fractions. For the fraction on the left hand side, the numerator is calculated in the following way. We collect into a set the degrees d′ that are cardinalities of some locals x hired by Huawei. max maps the set of d′-s to the maximum of the set, i.e., the cardinality of all locals hired by Huawei. Then, we collect into a set the degrees d that contain the maximum as an atomic part. min maps the set of d-s to the minimum, which is the degree that only contains the maximum of the set of d′-s as a part. As a result, min returns the cardinality of all locals hired by Huawei, which is the numerator. The denominator is calculated in the same way and it is the cardinality of all locals in the relevant place. The fraction consisting of the numerator and the denominator equals on the right hand side. It amounts to the meaning that all the locals hired by Huawei make up 40% of all locals in a contextually given place. This is the desired truth condition of the conservative reading of (29).12

Regarding tripartite quantificational structures (Heim 1982; Partee 1991; von Fintel 1994; a.o.), the proportional quantification induced in (30) is restricted by the NP complement of the RM phrase, i.e., locals, while the rest part of the sentence serves as the nuclear scope. This quantificational structure is typically conservative.

3.3 Deriving non-conservative readings

This subsection shows how the proposal of proportional number expressions accounts for more puzzling non-conservative readings. The key insight is that a proportional number expression has a potential to take scope beyond the RM phrase hosting it. At first glance, outside an RM phrase, there is no appropriate target for the scope taking of a proportional number expression. For concreteness, the type (d → Q) → Q dictates that a proportional number expression must scope over a constituent of type Q that dominates it. The logical form of (31), as shown in Figure 3, doesn’t provide such a target position outside of the RM phrase.

    1. (31)
    1. Huáwéi
    2. Huawei
    1. gù-le
    2. hire-prf
    1. 30%
    2. 30%
    1. de
    2. de
    1. BĚNDÌ-RÉN.
    2. local-people
    1. ‘Huawei has hired 30% locals.’                      (non-conservative)
Figure 3
Figure 3

The proportional number expression fails to find an appropriate scope position.

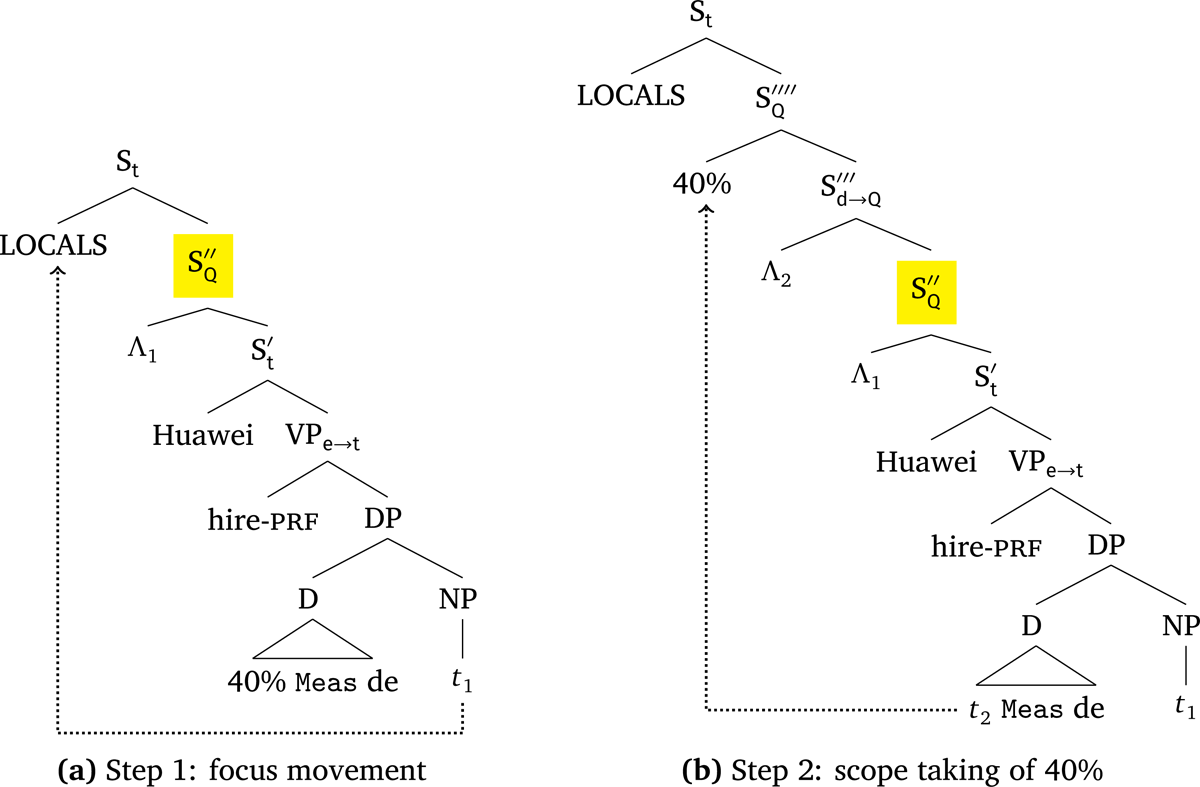
However, the problem shown in Figure 3 in fact offers a justification for the necessity of focusing the NP complement in the derivation of the non-conservative reading of (31). According to the movement approach to focus interpretation defended by Drubig (1994), Lee (2005), Krifka (2006), Wagner (2006), Tomaszewicz (2015), and Erlewine & Kotek (2017), a focused phrase undergoes LF movement, which triggers Λ-abstraction in the same way that QR does, as depicted in Figure 4a. As a result, the covert focus movement creates an intermediate node labelled S″. This node then serves as the scope target for 40%, which raises to yield the LF in Figure 4b. The scope taking of 40% also triggers a λ-abstraction (Λ2) over the trace t2, yielding a constituent S″′. Semantically, S″′ has the type d → Q and is taken as the scope argument by 40%.13

Figure 4
Figure 4

Parasitic scope.

Based on the LF in Figure 4b, combining 40% with S″′ gives rise to a function of type Q, as in (32). It should be noticed that the rest of the RM phrase, which is a quantifier, also takes scope within S″′. The resulting function takes the focused phrase as an argument and returns the desirable truth condition, as shown in (33).

    1. (32)
    1. (33)

In this example, the interpretation of gc depends on the focus value of the NP complement. gc is interpreted as a set of people including both locals and non-locals. I will show how the value of gc is determined towards the end of this section. All in all, (33) says: the cardinality of all locals hired by Huawei is the degree d1 (i.e., denominator); the cardinality of all people hired by Huawei is the degree d2 (i.e., numerator); and d1 divided by d2 equals 40%. This is the non-conservative reading: 40% of the people hired by Huawei are locals.

The scope pattern illustrated in Figure 4 is typically parasitic scope (Barker 2007; see also Sauerland 1998). The scope target for 40% does not exist until the focused NP has moved covertly. Then, the proportional number expression can scope between the focused argument and its semantic argument. In this sense, the scope of 40% is parasitic on the covert focus movement of the NP complement. Therefore, if the NP complement were not focused, the covert movement would not be activated. This is the reason why non-conservative readings are available only when the NP complements of RM phrases bear focus.

The proportional quantification in (33) expresses the proportion of Huawei’s local employees in its entire employee population. The latter provides the restrictor, while the former serves as the nuclear scope. Such a quantification echoes the well-known focus mapping hypothesis of a quantificational structure (Partee 1991; von Fintel 1994; Herburger 1997; 2000; a.o.): focus materials are mapped to the nuclear scope, while non-focused materials are mapped to the restrictor. In addition, the proportional quantification in (33), which underlies a non-conservative reading, just reverses the restrictor and the nuclear scope of the one in (30), which yields a conservative reading. This is along the lines with Ahn & Sauerland (2017). The apparent non-conservative reading is derived from the conservative proportional quantification in (33), which can be paraphrased as: 40% of the people hired by Huawei are locals hired by Huawei.

Finally, let’s turn to the contribution of the focus value of the NP complement. Rooth (1985; 1992) proposes that focus evokes alternatives in a different dimension of meaning from the ordinary meaning. For example, LOCALS as a focused NP denotes a property as its ordinary meaning and a set of alternative properties as its focus value, represented by . The two values converge when a focus interpretation operator ∼, defined as in (34), applies to X and its definedness condition is satisfied.

    1. (34)

∼ introduces a contextually given set c, which must be a subset of the focus value of the constituent that it combines with. In an RM construction with a non-conservative reading, the RM phrase is constructed as in (35).

    1. (35)
    1. [[40%∪c]-de [LOCALS ∼ c]]

The focus value of LOCALS, i.e., , contains different properties of type e → t. The variable c is a subset of and fixed contextually, for example, c may be {λx.locals(x), λx.non-locals(x)}. Like other focus sensitive adverbs, such as only and always (Rooth 1992; von Fintel 1994), the proportional number expression can be restricted by the union of c.

With this in mind, let us look at the sentence in (31) again, whose LF is given in (36). In the present analysis, this LF derives the meaning formulated in (37). The denominator involves the measurement of all the people (locals and non-locals, x ∈ ∪gc) hired by Huawei. The resulting representation precisely captures the desired meaning.

    1. (36)
    1. [LOCALS ∼ c] [S″′ 40%∪c [S″′ Λ2 [S′ Λ1 [S Huawei hire-prf [[t2-Meas de] t1]]]]
    1. (37)

As a consequence, the present analysis can be extended to so-called ‘narrow focus’ readings observed in Ahn & Sauerland (2017) and Pasternak & Sauerland (to appear). Consider (38). It expresses the ratio of engineers from the US to all engineers rather than all employees, when focus is narrowed down to měigúo ‘the US’.

    1. (38)
    1. Huáwéi
    2. Huawei
    1. gù-le
    2. hire-prf
    1. 10%
    2. 10%
    1. de
    2. lnk
    1. MĚIGÚO
    2. U.S.
    1. gōngchéngshī.
    2. engineers
    1. ‘10% of the engineers hired
    2.  
    1. ‘10% of the engineers hired by Huawei come from the US.’

In this example, the focus feature of US triggers covert pied-piping of the whole NP complement, as suggested in Drubig (1994) and Erlewine & Kotek (2017). Therefore, the LF is derived as in (39), where 10% is restricted by the union of a subset c of .

    1. (39)
    1. [US engineers ∼ c] [S″′ 10%∪c [S″ Λ2 [S′ Λ1 [S Huawei hire-prf [[t2-Meas de] t1]]]]

So, c may be {λx.from.US(x)∧engineers(x), λx.from.China(x)∧engineers(x)}. Unioning the sets in c gives rise to a set of engineers from the US and China. Thus, the relative measurement expressed by (38) only concerns engineers, not other kinds of employees.

3.4 Accounting for scope interactions

According to the proposed compositional analysis, a ‘non-conservative’ RM phrase must take three steps to outscope another scope-bearing element (SBE) c-commanding it. The three steps are represented as in (40). Step 1, the NP complement undergoes covert focus movement across the scope-bearing element, creating a scope target for the proportional number expression n%. Step 2, n% takes scope over the scope-bearing element. Step 3, the remnant of the RM phrase continuously scopes above the scope-bearing element.

    1. (40)
    1. Step 1: [NP Λ1 [s … … [DP [n%-Meas de ] t1]]]
    2. Step 2: [NP [n% Λ2 [Λ1 [ … … [DP [t2-Meas de ] t1]]]]]
    3. Step 3: [NP [n% Λ2 [Λ1 [[DP [t2-Meas de ] t1] Λ3 [s … … t3 ]]]]]

Note that n% must scope out of the RM phrase before the latter takes scope. Due to type mismatch, the denotation of the RM phrase cannot be computed successfully if n% stays in situ. In this sense, the wide scope of an RM phrase must be derived through an intermediate representation in which the proportional number expression has been raised to its scope position.

It has been observed that degree quantifiers have difficulty scoping above other scope-bearing elements (Szabolcsi & Zwarts 1992; Kennedy 1997; Heim 2000; Takahashi 2006; Lassiter 2012 a.o.). Along similar lines, I will show in the following subsections that the LF representation in Step 2 is illegitimate, because it leads to undefinedness in semantic interpretation. Takahashi (2006) suggests that the legitimacy of an LF induced by scope taking is checked immediately (see also Tomaszewicz 2015). Even though subsequent scope taking operations may ultimately return well-formed LFs, issues from an intermediate stage still affect grammaticality. Following this view, the LF in step 2 is illegitimate so that the LF in step 3 is not allowed. Consequently, the wide scope of the RM phrase is not available.

By contrast, a ‘conservative’ RM phrase take wide scope relative to another scope-bearing element in two steps. Step 1, the proportional number expression takes DP-internal scope. Step 2, the whole RM phrase scopes across the scope-bearing element, piped-piping the proportional number expression. The process is illustrated in (41).

    1. (41)
    1. Step 1: [s … … [n% Λ1 [DP [t1-Meas de ] NP ]]]
    2. Step 2: [[n% Λ1 [DP [t1-Meas de ] NP ]] Λ2 [s … … t2 ]]

As a result, the scope-bearing element outside the RM phrase does not intervene between the proportional number expression and its trace. In other words, the scope-bearing element does not interfere with the scope taking of the degree quantifier denoted by the proportional number expression. Hence, as we observed, a ‘conservative’ RM phrase can scope above another scope-bearing element, such as negation or an intensional operator.

In short, the present analysis of the scope contrast crucially relies on the constraint preventing a degree quantifier from outscoping another scope-bearing element. To my knowledge, this constraint has not received a widely agreed account, even though many studies tried to tackle this issue (Szabolcsi & Zwarts 1992; Stateva 2004; Takahashi 2006; Lassiter 2012). It is beyond the scope of the paper to provide an analysis of the constraint covering all the degree-related constructions, including comparatives and degree questions. Instead, the following subsections show how the specific definition of proportional number expressions defended in this paper is not compatible with the LF representation in Step 2 in (40).

3.4.1 Negation

Recall that negation must take wide scope relative to ·non-conservative’ RM phrases. The relevant example is repeated in (42).

    1. (42)
    1. Huáwéi
    2. Huawei
    1. méiyǒu
    2. not
    1. gù
    2. hire
    1. 70%
    2. 70%
    1. de
    2. lnk
    1. BĚNDÌ-RÉN.
    2. local-people
    1.  
    1. a.
    1.   Non-conservative: not > 70% locals:
    2.   ‘It’s not the case that 70% of Huawei’s employees were locals.’
    1.  
    1. b.
    1. #Non-conservative: 70% locals > not
    2.   ‘70% of the people that Huawei didn’t hire were locals.’

The present analysis requires a ‘non-conservative’ RM phrase to take wide scope in the following three steps. For simplicity, we assume that the negative item, as a propositional operator, always take sentential scope at LF. In step 2, the negative item intervenes between the proportional number expression and its trace. The LF produces the logical representation in (44).

    1. (43)
    1. Step 1: [LOCALS Λ1 not [[Huawei hire-prf [70%-Meas t1]]]]
    2. Step 2: [LOCALS [70% Λ2 [Λ1 not [[Huawei hire-prf [t2-Meas t1]]]]]]
    3. Step 3: [LOCALS [70% Λ2 [Λ1 [[t2-Meas t1] Λ3 not [[Huawei hire-prf t3]]]]]]
    1. (44)

Both sets operated on by min include all degrees other than the cardinalities of the relevant employees of Huawei, i.e., including all degrees exceeding the cardinalities of these employees. Such sets are infinite so that we cannot find the unique minimal degree plurality. As a consequence, the application of min to these sets will be undefined. Hence, the LF in Step 2 is not well-formed and the subsequent LF in Step 3 is prevented. The wide scope reading of the RM phrase is not available.

It should be noted that in (43) the meaning of the RM phrase cannot be derived when 70% stays inside it. This is because 70% as a degree quantifier cannot combine with Meas (see Section 3.2). As a result, the scope taking of the RM phrase must follow the scope taking of 70%. In this derivation, furthermore, the focused NP complement must move first, creating a scope position for 70%. Consequently, the order of the steps in (43) cannot be changed.

By contrast, in the narrow scope interpretation, the proportional number expression should scope under the negative item, as illustrated by the following steps.

    1. (45)
    1. Step 1: [not [LOCALS Λ1 [Huawei hire-prf [70%-Meas t1]]]]
    2. Step 2: [not [LOCALS [70% Λ2 [Λ1 [Huawei hire-prf [t2-Meas t1]]]]]]
    3. Step 3: [not [LOCALS [70% Λ2 [Λ1 [[t2-Meas t1] Λ3 [Huawei hire-prf t3]]]]]]

As a result, the negative item does not interfere with the relation of 70% and its trace The problem in (43) does not appear here.

The scope restriction is not observed for ‘conservative’ RM phrases. Consider (46a), in which the RM phrase can take wide or narrow scope relative to the negative item. In the present analysis, the wide scope reading is derived as in (47).

    1. (46)
    1. Huáwéi
    2. Huawei
    1. méiyǒu
    2. not
    1. gù
    2. hire
    1. 70%
    2. 70%
    1. de
    2. lnk
    1. běndì-rén.
    2. local-people
    1.  
    1. a.
    1. Conservative: not > 70% locals
    2. ‘It is not the case that Huawei hired 70% of the locals.’
    1.  
    1. b.
    1. Conservative: 70% locals > not
    2. ‘70% of the locals were such that Huawei didn’t hire them.’
    1. (47)
    1. a.
    1. Step 1: [not [Huawei hire-prf [70% Λ1 [t1-Meas locals]]]]
    1.  
    1. b.
    1. Step 2: [[70% Λ1 [t1-Meas locals]] Λ2 [not [Huawei hire-prf t2]]]

In this derivation, the proportional number expression scopes at the edge of the RM phrase hosting it. The negative item outside the RM phrase does not interfere with the relation of the proportional number expression and its trace, either, as shown in (45). As a result, the scope taking of the RM phrase in Step 2 can be conducted successfully. Thus, the wide scope interpretation of the RM phrase is available when the RM construction is understood as a conservative reading.

3.4.2 Intensional operators

Section 2 has demonstrated that ‘non-conservative’ RM phrases must take narrow scope relative to intensional verbs. A relevant example is repeated in (48). The non-conservative de re reading is not available.

    1. (48)
    1. Huáwéi
    2. Huawei
    1. xiǎng
    2. want
    1. zhào
    2. recruit
    1. sānfēnzhīyī
    2. one.third
    1. de
    2. lnk
    1. RUǍNJIÀN
    2. software
    1. gōngchéngshī.
    2. engineers
    1.  
    1. a.
    1.   Non-conservative de dicto: want > one third software engineers
    2.   ‘For all worlds w compatible with Huawei’s desire in the actual world w0, it recruits one third SOFTWARE engineers in w.’
    1.  
    1. b.
    1. #Non-conservative de re: one third software engineers > want
    2.   ‘There’re some people X such that for all worlds w compatible with Huawei’s desire in the actual world w0, it recruits X in w; One third of X are software engineers’

The derivation of the non-conservative de re reading consists of three steps. First, the focused NP complement moves at LF and adjoins to the root of the sentence, creating a node higher than the intersional verb. Second, the proportional number expression scopes at the edge of the newly-created node. Third, the remnant of the RM phrase is QR-ed across the intersional verb. Crucially, the second step produces the LF in (49).

    1. (49)

The scope argument of one third is a function from degrees to quantifiers, i.e., (50).14 Feeding the function to one third and then combining the result with the predicate denoted by the focused NP yields the truth condition in (51).

    1. (50)
    1. λdλP∀w ∈ 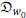(h): max{d′ : ∃x.P(x)(w) ∧ recruitw(x)(h) ∧ gμ(x) = d′ ⊑ d
    1. (51)

As standardly assumed, the intensional verb want denotes a universal quantifier over possible worlds. 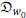(h) stands for a set of possible worlds that are compatible with Huawei’s desire. At LF, want scopally embeds the remnant of the RM phrase, inducing a de dicto interpretation. So, for every possible world w compatible with Huawei’s desire, there is a maximal set of people recruited by Huawei in w. For (51), the numerator is the minimum of the set of degrees that contain at least the cardinalities of all the sets of software engineers recruited by Huawei across possible worlds. Suppose that Huawei recruits 10 software engineers in w1, 20 in w2 and 40 in w3, the minimum should be 10⊔20⊔40. However, the operation of division is not defined for plural degrees. Hence, the representation in (51) is not well-formed when the number of the software engineers recruited by Huawei varies among different possible worlds. So, as Takahashi (2006) assumes, the LF in (49) is prevented and the following step of QR-ing the remnant RM phrase across want is also banned. The same problem also applies to the denominator in (51).

Of course, this problem does not arise if Huawei recruits the same number of software engineers (and the same number of all engineers) in every possible world. The minimum is an atomic degree. Therefore, it would be the case that the wide scope of the RM phrase is allowed if Huawei wants to recruit the same number of software engineers. Nevertheless, it is not borne out. In order to address this issue, I suggest that the meaning of a proportional number expression have a definedness condition that prohibits the scope argument of the proportional number expression from leading to a non-atomic degree as the minimum in any situation. Concretely, the lexical entry of a proportional number expression can be revised as follows.15

    1. (52)
    1. Definition of proportional number expressions (final, intersional version)

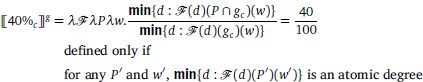
Generally, if the scope argument of a proportional number expression is provided by a LF constituent in which a universal quantifier scopes over the remnant of the relevant RM phrase, as exemplified by (50), the definedness condition is not fulfilled. The formal reason is that the quantifier denoted by the RM phrase always can exhibit variation of witness sets when scoping under a universal quantifier (see Beghelli et al. 1997). This leads to variation of the degrees associating with the witness sets. As a result, it cannot be guaranteed that the ‘atomicity’ requirement is satisfied in all possible worlds.16

The narrow scope interpretation of (48) is achieved by scoping the proportional number expression below want. Following the standard analysis of a control verb, want takes as its complement a clause that contains a null pronoun PRO co-indexed with the subject. Therefore, both the NP complement and one third can scope at the edge of the embedded clause, as shown below. The intensional verb does not intervene between one third and its trace. The problem in (50) does not arise.17

    1. (53)
    1. [Huawei1 want [[SW engineers] [[one third] Λ2 [Λ1 [PRO1 recruit [t2-Meas t1]]]]]]

Turning to an RM construction with a conservative reading, the RM phrase can scope above or below an intensional verb (see Section 2). That is, both de re and de dicto readings are available. This is expected in the present analysis. In the derivation of a conservative reading, the proportional number expression only takes DP-internal scope so that no intensional verb will intervene between the proportional number expression and the variable bound by it.18

3.4.3 Quantificational DPs

In the end, let’s move to the cases involving scope interactions of quantificational DPs and RM phrases. Siding with the cases discussed in the last two subsections, a ‘non-conservative’ RM phrase cannot outscope any quantificational DP. For example, in (54), only the narrow scope reading is available for the ‘non-conservative’ RM phrase.

    1. (54)
    1. Zhěnghǎo
    2. exactly
    1. yǒu
    2. have
    1. liǎng-gè
    2. two-cl
    1. xuéshēng
    2. students
    1. dú-le
    2. read-prf
    1. sānfēnzhīyī
    2. one.third
    1. de
    2. lnk
    1. XIǍOSHŪO
    2. novels
    1. (sānfēnzhīèr
    2. two.thirds
    1. de
    2. lnk
    1. ZÁZHÌ).
    2. magazines
    1.  
    1. a.
    1.   Non-conservative: exactly two students > one third novels
    2.   ‘There are exactly two students such that they each read one third NOVELS (and two thirds MAGAZINES).’
    1.  
    1. b.
    1. #Non-conservative: one third novels > exactly two students
    2.   ‘One third of the books that exactly two students read were NOVELS. (Two thirds of the books that exactly two students read were MAGAZINES.)’

In order to derive the wide scope interpretation, we should first generate the following LF, where the exactly-DP occurs between one third and its trace.

    1. (55)
    1. [NOVELS [[one third] Λ2 [Λ1 exactly 2 students read-prf [t2-Meas t1]]]]

The scope argument of the proportional number expression denotes the function in (56). The set of degrees d characterized by this function lacks the unique minimum. To see this, say that there are only four students who read books; two of them both read 30 books and the other two 60 books. Then, we have a set of plural degrees—some of which contain 30 as an atomic part, some of which contain 60 as an atomic part, and some of which contain both.

    1. (56)
    1. λdλP∃!x.stdts(x) ∧ |x| = 2 ∧
    2.                              ∀x′ ⊏atom x : max{d′ : ∃y.P(y) ∧ read(y)(x′) ∧ gμ(y) = d′} ⊑ d

After the function is fed to one third, min encoded in the lexical entry of one third is applied. It must pick up the unique minimum from the set of degrees d that contain 60, 30 or both as an atomic part. However, it yields undefinedness, since there are two d-s in the set that have no parts that are also in the set, namely 30 and 60. As a result, the LF in (55) is not legitimate. The subsequent scope taking of the remnant of the RM phrase is blocked.

In fact, it is not just non-monotone quantifiers that create multiple minima. Any non-universal quantifier, such as most-DPs and existential DPs, would result in undefinedness. So, it is expected that an RM phrase cannot scope outside non-universal quantifiers. For a universal quantifier like an every-DP, once it scopally intervenes between a degree quantifier and its degree variable, the definedness condition that prohibits variation of the value of the degree variable (see the last subsection) is not satisfied. Consequently, in the derivation of a non-conservative reading, the relevant RM phrase is prevented from outscoping a universal quantifier. The formal reasoning is the same as the one given in the last subsection that shows why the intensional verb want, which gives rise to a universal quantification over possible worlds, cannot scope below an RM phrase. I leave it for the reader to verify the scopal restriction.

Interestingly, the obligatory narrow scope effect seems to appear in a sentence where a ‘conservative’ RM phrase is c-commanded by another quantificational DP, as evidenced by (57) (repeating (18)).

    1. (57)
    1. Zhěnghǎo
    2. exactly
    1. yǒu
    2. have
    1. liǎng-gè
    2. two-cl
    1. xuéshēng
    2. students
    1. dú-le
    2. read-prf
    1. sānfēnzhīyī
    2. one.third
    1. de
    2. lnk
    1. xiǎoshūo.
    2. novels
    1.  
    1. a.
    1.    Conservative: exactly two students > one third novels
    2.    ‘There are exactly two students such that each of them read one third of the novels.’
    1.  
    1. b.
    1. ??Conservative: one third novels > exactly two students
    2.    ‘One third of the novels are the ones red by exactly two students.’

This phenomenon is contrary to the prediction of the present analysis. According to the proposed derivation of conservative readings, the proportional number expression in (54) is not raised out of the RM phrase but is pied piped when the whole RM phrase is QR-ed. As a result, the exactly-DP only interacts with the whole RM phrase in terms of scope. Since both phrases are quantifiers over entities, it remains unclear why scoping the RM phrase above the exactly-DP is inhibited.

This scopal puzzle is not unqiue to ‘conservative’ RM phrases. Modified numerals usually do not take scope over quantificational DPs c-commanding them (Liu 1990; Beghelli 1995; Beghelli & Stowell 1997; Szabolcsi 1997; Hackl 2000; Takahashi 2006; a.o.). This generalization is attested cross-linguistically, as exemplified in (58) (Mandarin) and (59) (English).19 None of the examples may imply that there were specific books read by students.20

    1. (58)
    1. Zhěnghǎo
    2. exactly
    1. yǒu
    2. have
    1. liǎng-gè
    2. two-cl
    1. xuéshēng
    2. students
    1. dú-le
    2. read-prf
    1. shí-duō
    2. ten-more
    1. běn
    2. cl
    1. shū.
    2. books
    1.  
    1. a.
    1.   exactly two students > more than 10 but less than 20 books
    2.   ‘There are exactly two students such that each of them read more than 10 but less than 20 books.’
    1.  
    1. b.
    1. #more than ten books > exactly two students
    2.   ‘There are more than 10 but less than 20 books such that exactly two students read each of them.’
    1. (59)
    1. a.
    1. Every student in this class read more than three books.
    2.                                           (every >/*< more than 3)
    1.  
    1. b.
    1. One student in this class read fewer than three books.
    2.                                           (one >/*< fewer than 3)

In addition, the scope-taking parallelism is further confirmed from another direction: similar to a ‘conservative’ RM phrase, a modifier numeral can scope over a negative item or an intensional verb, as visualized in (60) and (61). Takahashi (2006) also notices that modifier numerals in English exhibit scope ambiguities relative to negation, as in (62).

    1. (60)
    1. Lǐbái
    2. Libai
    1. méi
    2. not
    1. dú
    2. read
    1. shí-duō
    2. ten-more
    1. běn
    2. cl
    1. shū.
    2. books
    1.  
    1. a.
    1. not > more than 10 but less than 20 books
    2. ‘It is not the case that Libai read more than 10 but less 20 books.’
    1.  
    1. b.
    1. more than 10 but less than 20 books > not
    2. ‘There are more than 10 but less 20 books that Libai has not read.’
    1. (61)
    1. Lǐbái
    2. Libai
    1. xiǎng
    2. want
    1. dú
    2. read
    1. shí-duō
    2. ten-more
    1. běn
    2. cl
    1. xiǎshuō.
    2. novels
    1.  
    1. a.
    1. want > more than 10 but less than 20 books
    2. ‘For any possible world w compatible with Libai’s desire, he reads more than 10 but less 20 novels in w.’
    1.  
    1. b.
    1. more than 10 but less than 20 books > want
    2. ‘There are more than 10 but less than 20 books such that Libai reads them in all possible worlds compatible with his desire.’
    1. (62)
    1. John doesn’t speak more than three (of the) languages. (not >/< more than 3)

Regarding parallel scope possibilities, ‘conservative’ RM phrases pattern like modified numerals. There may be general principle that allows the quantity expressions to scope above or below scope-bearing non-DP elements but prevents them from outscoping quantificational DPs.21 Since the present study focuses on RM phrases, exploring this potential general principle has to be left for another occasion.22

4 Extensions

In the proposed analysis, the focused NP complement of a ‘non-conservative’ RM phrase undergoes covert movement, which creates the scope target for the proportional number expression. This section discusses two phenomena involving syntactic factors and shows that the covert movement is not only crucial to the DP-external scope taking of a proportional number expression, but also sheds light on some structural issues.

4.1 Dislocation constructions

For a ‘non-conservative’ RM phrase, the proportional number expression takes scope after the NP complement undergoes covert focus movement. At LF, the scope position of the proportional number expression immediately follows the dislocated NP. In fact, the dislocation of the NP complement is not always covert. As exemplified in (63), it can be overtly observed.

    1. (63)
    1. Běndì-rén,
    2. local-people
    1. Huáwéi
    2. Huawei
    1. gù-le
    2. hire-asp
    1. 40% e1.
    2. 40%
    1.  
    1. a.
    1. ‘Huawei has hired 40% of the locals.’                                               (conservative)
    1.  
    1. b.
    1. ‘Huawei has hired 40% locals.’                                                 (non-conservative)

This sentence is also ambiguous between a conservative and a non-conservative reading. In this subsection, I show that the ambiguity in dislocation constructions can be captured directly by the present analysis.

Mandarin has a number of dislocation constructions, such as topic or focus constructions, where topic or focus elements are dislocated from base generated positions to positions in the left periphery. Accordingly, in (63), the proportional number expression is followed by e, which is co-indexed with the sentence initial NP. For this study, it does not matter very much how the relation between the NP and e is established. Specifically, e could be a trace left by movement of the NP, or a null pronominal expression bound by the NP. For simplicity, I abstract away from the topic or focus status of the dislocation and assume that the dislocated NP triggers a Λ abstraction over the values assigning to e at LF, as visualized in (64).

    1. (64)
    1. [s locals Λ1 [s Huawei hire-prf [DP 40%-Meas e1]]]

Based on the LF, the ‘non-conservative’ reading is naturally derived. The proportional number expression scopes between the dislocated NP and the λ abstraction Λ1, as shown in (65). In this sense, the dislocation of the NP plays the same role as covert focus movement of NP complements in ordinary RM constructions.

    1. (65)

The ‘conservative’ reading corresponds to the LF in (66). The proportional number expression scopes at the edge of the RM phrase and the whole RM phrase takes scope. The λ-abstraction Λ1 reconstructs the property ⟦locals⟧ back into the RM phrase. Consequently, the LF leads to the conservative reading.

    1. (66)

Interestingly, the non-conservative reading in (63) disappears when the dislocated element becomes a definite expression. As demonstrated in (67), the dislocated NP is a demonstrative phrase and the sentence only has a conservative reading.23

    1. (67)
    1. Zhè-xiē
    2. this-cl
    1. běndì-rén,
    2. local-people
    1. Huáwéi
    2. Huawei
    1. gù-le
    2. hire-prf
    1. 40%.
    2. 40%
    1.  
    1. a.
    1.   ‘Huawei has hired 40% of these locals.’                                             (conservative)
    1.  
    1. b.
    1. #‘These locals hired by Huawei makes up 40% of the employees of Huawei.’                                             (non-conservative)

The demonstrative phrase denotes an entity of type e. According to the present analysis, if (67) had a ‘non-conservative’ reading, this reading would result from the LF in (68). Here the λ-abstraction Λ1 creates a predicate of type e → t, rather than a quantifier. Hence, Λ1 fails to create an appropriate scope position for the proportional number expression.

    1. (68)

The problem is why the ‘conservative’ reading is preserved. If the LF of (67) were analyzed as (69), the semantic computations would run into the problem of type mismatch. For concreteness, in (69), the entity denoted by these locals is reconstructed into the position of e1. However, the functional head Meas requires a property, not an entity.

    1. (69)

In fact, the dislocation construction in (67) is related to an RM construction with a partitive expression. A typical instance of Mandarin partitive expressions is given in (70), where the demonstrative phrase occurs before the proportional number expression.

    1. (70)
    1. Huáwéi
    2. Huawei
    1. gù-le
    2. hire-prf
    1. zhè-xiē
    2. this-cl
    1. běndì-rén
    2. local-people
    1. de
    2. lnk
    1. 40%.
    2. 40%
    1. ‘Huawei has hired 40% of the locals.’

According to Jin (2015), a phrase with the structure ‘DP de Number’ is the counterpart of English partitives like 40% of the locals. Her study convincingly shows that such a phrase, rather than the one with the structure ‘Number lnk NP’, exhibits distinguished features of partitives. Therefore, the object phrase in (70) is a partitive expression and different from RM phrases. Crucially, it does not evoke a non-conservative reading.

I propose that (67) is construed as (71). The dislocated demonstrative phrase is co-indexed with an empty element preceding the proportional number expression. Hence, the semantic reconstruction of the demonstrative phrase enables us to compute the meaning of (71) in a way similar to (70). Notice that the morpheme de must be attached to an overt item, so the null pronoun in (71) does not support the attachment.

    1. (71)
    1. [Zhè-xiē
    2. this-cl
    1. běndì-rén]1,
    2. local-people
    1. Huáwéi
    2. Huawei
    1. gù-le
    2. hire-prf
    1. e1
    2.  
    1. 40%.
    2. 40%

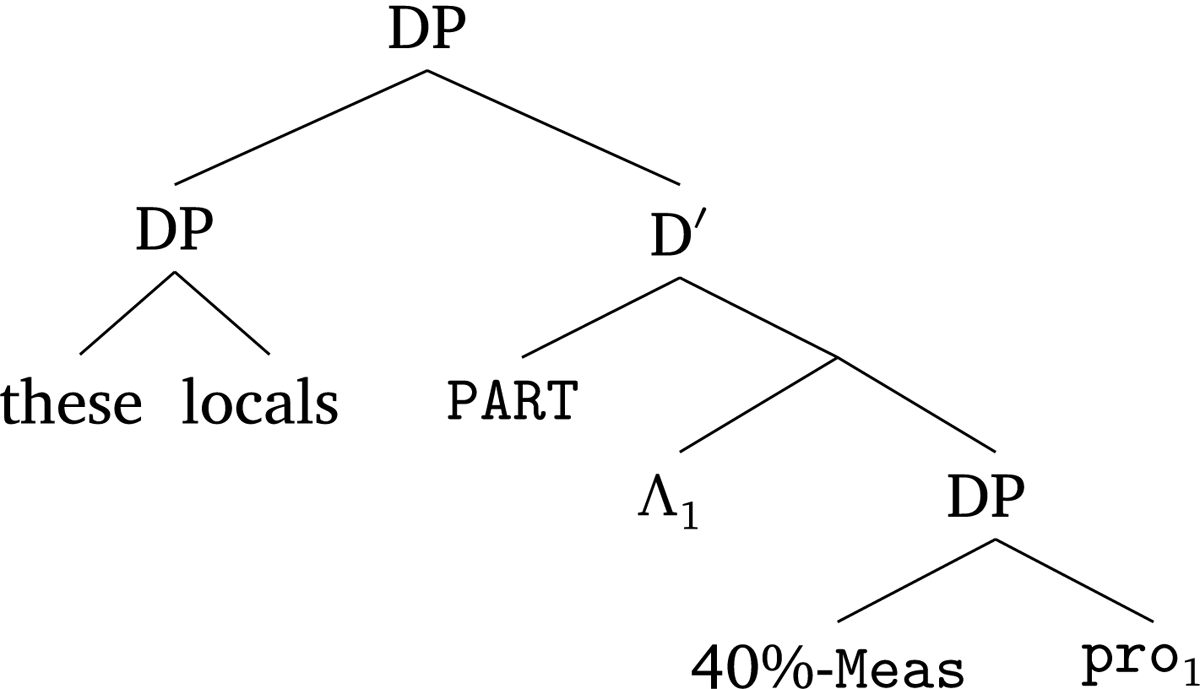
I postulate that the structure of the partitive expression is built upon the RM phrase, as shown in Figure 5. Concretely, PART is a null functional head taking an RM phrase (or a quantity expression in general) as the complement and a DP as the specifier. The complement of 40%-Meas is a null pronoun referring to a property and being bound by the Λ operator.

Figure 5
Figure 5

The structure of partitive expressions.

Correspondingly, PART denotes a function mapping an object of type (e → t) → Q and a DP of type e to a quantifier, as in (72). The denotation of the phrase in Figure 5 is computed in a way shown in (73). According to the present analysis of relative measurement, the partitive expression denoting a quantifier only gives rise to a conservative reading.

    1. (72)
    1. (73)

Returning to (71), the demonstrative phrase is reconstructed into the specifier of PART. According to the computation in (73), the sentence contains a ‘conservative’ RM phrase and hence receives a conservative reading.

(71) does not have a non-conservative reading. The main reason is that the complement of ‘40%-Meas’ is a null pronoun, which cannot be focused. In my analysis, the sentential scope of a proportional number expression is parasitic on the covert focus movement of the NP complement of the RM phrase. As the null pronoun cannot be focused, the proportional number expression is not able to take the sentential scope and hence the non-conservative reading is impossible to be generated.

4.2 A structural asymmetry

Ahn & Sauerland (2017) notice that the non-conservative reading of an RM construction in Mandarin exhibits an intriguing subject-object asymmetry. As in (74), the non-conservative reading does not appear when an RM phrase occurs in the subject position.

    1. (74)
    1. 30%
    2. 30%
    1. de
    2. lnk
    1. kuàgúo
    2. international
    1. gōngsī
    2. companies
    1. gù-le
    2. hire-prf
    1. běndì-rén.
    2. local-people
    1.  
    1. a.
    1.   ‘30% of the international companies hired locals.’                                                                    (conservative)
    1.  
    1. b.
    1. #‘30% of the companies hiring locals were international ones.’                                          (non-conservative)

The generalization about the subject–object asymmetry is further verified by the fact that the non-conservative reading is unavailable when RM phrases are derived subjects. In particular, the RM phrase is the subject of the passive in (75) and the non-partitive reading is unavailable.

    1. (75)
    1. 40%
    2. 40%
    1. de
    2. lnk
    1. běndì-rén
    2. local-people
    1. bèi
    2. psv
    1. Huáwéi
    2. Huawei
    1. gù-le.
    2. hire-prf
    1.  
    1. a.
    1.   ‘40% of the locals have been hired by Huawei.’                                               (conservative)
    1.  
    1. b.
    1. #‘40% of people hired by Huawei were locals.’                                          (non-conservative)

Regarding unaccusative verbs, the non-conservative reading is allowed when an RM phrase stays in the post-verbal (or object) position, as in (76a), but becomes absent when the RM phrase moves to the pre-verbal (subject) position, as in (76b).

    1. (76)
    1. a.
    1. Dǎo-le
    2. fall-prf
    1. yíbàn
    2. half
    1. de
    2. lnk
    1. xiàngshù.
    2. oaks
    1.  
    1. (i)
    1. ‘Half of the oaks fell.’
    1.  
    1. (ii)
    1. ‘Half of the falling trees were oaks.’
    1.  
    1. b.
    1. Yíbàn
    2. half
    1. de
    2. lnk
    1. xiàngshù
    2. oaks
    1. dǎo-le.
    2. fall-prf
    1.  
    1. (i)
    1. ‘Half of the oaks fell.’
    1.  
    1. (ii)
    1.  #‘Half of the falling trees were oaks.’

Actually, the asymmetry is not restricted to subjects and objects. When an object RM phrase is topicalized, only a conservative reading is allowed, as shown in (77). In addition, it is the same case when an RM phrase occurs in a PP adjunct, as shown in (78).24

    1. (77)
    1. 40%
    2. 40%
    1. de
    2. lnk
    1. qìchē
    2. car
    1. chǎngfáng,
    2. factories
    1. wǒmén
    2. we
    1. yǐjīng
    2. already
    1. wéixiū
    2. repair
    1. wǎnbì-le.
    2. finish-prf
    1.  
    1. a.
    1.   ‘We have repaired 40% of the car factories.’                                           (conservative)
    1.  
    1. b.
    1. #‘40% of the factories we have repaired are car factories.’                (non-conservative)
    1. (78)
    1. Zhèngfǔ
    2. government
    1. [PP
    2.  
    1. gěi
    2. to
    1. 40%
    2. 40%
    1. de
    2. lnk
    1. běndì-rén]
    2. local-people
    1. fēnpèi-le
    2. assign-asp
    1. gōngwū.
    2. public.housing
    1.  
    1. a.
    1.   ‘The government has assigned public housing to 40% of the locals.’
    1.  
    1. b.
    1. #‘40% of the people that the government assigned public housing to were locals.’

In short, the structural asymmetry is observed between a pre-verbal position and a post-verbal position. A post-verbal RM phrase is compatible with a conservative reading and a non-conservative reading, whereas a pre-verbal RM phrase is only compatible with a conservative reading.

In the present analysis, a non-conservative reading is generated from an RM construction only when the NP complement of the RM phrase undergoes covert focus movement, which creates a scope target for the proportional number expression. If the covert movement is banned, then non-conservative readings would not appear. According to Erteschik-Shir (1977) and Diesing (1992), syntactic movement out of a nominal phrase is constrained by a presupposition condition: a lexical item cannot move out of a presuppositional nominal phrase. Moreover, in Mandarin, an indefinite appearing pre-verbally must be specific (Lee 1986; Xu 1996; Tsai 2001; a.o.). This kind of indefinite presupposes the existence of entities. In the present analysis, an RM phrase is decomposed into a proportional number expression and a measure phrase, which involves existential force and can be treated as an indefinite, as repeated below.

    1. (79)
    1. ⟦DP⟧g = λP.max{d′ : ∃xlocals(x) ∧ P(x) ∧ gμ(x) = d′} ⊑ g1                                             Type: Q

As a result, if an RM phrase is located in a pre-verbal position, the measure phrase must be presuppositional. Therefore, moving out of the NP complement is prevented by the presupposition condition. This explains why a non-conservative reading is blocked when an RM phrase occurs in a pre-verbal position.

5 Conclusion

Based on Mandarin, this paper has investigated the scope possibilities of RM phrases when they participate in the conservative and non-conservative readings of relative measurement. The main empirical finding is stated in the following generalization:

    1. (80)
    1. The scope generalization of an RM phrase
    2. A ‘conservative’ RM phrase can take wide scope over another scope-bearing element; whereas, a ‘non-conservative’ RM phrase is consistently confined to taking narrow scope.

Theoretically, this paper has offered a compositional analysis for the conservative and non-conservative readings of an RM construction. The main innovation lies in the decomposition of an RM phrase, i.e., an RM phrase consists of a proportional number expression and a measure phrase. The former denotes a degree quantifier, while the latter a counting quantifier. The proportional number expression can scope at two positions. On one hand, it can take scope at the edge of the RM phrase hosting it, giving rise to the conservative reading. On the other hand, it can take scope outside the RM phrase, targeting a position created by the covert focus movement of the NP complement of the RM phrase. The result is a non-conservative reading.

Building on previous studies on the scope of degree quantifiers (Kennedy 1997; Heim 2000; Takahashi 2006), the decompositional analysis has accounted for the scope generalization of RM phrases. Specifically, for a ‘non-conservative’ RM phrase, the proportional number expression scopes outside the RM phrase. As a degree quantifier, the proportional number expression is prevented from scoping over another scope-bearing element. Otherwise, the resulting LF leads to an undefined semantic representation. Consequently, following Takahashi (2006), the whole ‘non-conservative’ RM phrase cannot take wide scope relative the scope-bearing element. By contrast, a proportional number expression takes DP-internal scope in a ‘conservative’ RM phrase and hence it will not interact with a scope-bearing element outside the RM phrase. As a result, the scope of a ‘conservative’ RM phrase is not affected by the scope limitation of a proportional number expression.

The present study only involves Mandarin, but, as Ahn & Sauerland (2017) note, the conservative and non-conservative readings of RM constructions are observed in a wide variety of languages. It is natural to wonder what the scope pattern of an RM phrase is in languages other than Mandarin and whether the present decompositional analysis can be extended to these languages. The answers to these questions await a cross-linguistic investigation.

Notes

  1. Westerstahl (1985) notices that vague proportional quantifiers such as many-NPs and few-NPs also have a non-conservative reading. For example, the sentence Many SCANDINAVIANS won the Nobel price in literature, in which SCANDINAVIANS bears focus, can be paraphrased as: many people wining the Nobel price in literature are Scandinavians. However, Ahn & Sauerland (2015a) compare this phenomenon with the non-conservative reading of an RM phrase, pointing out that they may be independent to each other. So, in this paper, I will not dive into vague proportional quantifiers. [^]
  2. The acceptability of the non-conservative reading varies among speakers. A structured survey was conducted to clarify this issue. Although there were some participants who rejected non-conservative readings, the results largely verified the existence of these readings. The details of the survey are stored in Appendix A in the supplementary file. [^]
  3. The following abbreviations are used in the glossing: prf: perfective marker; lnk: linker; cl: classifier; psv: passive marker; dist: distributive adverb. [^]
  4. Note that all the data presented in this section and beyond are collected from introspective methods. [^]
  5. In (15), the fraction number expression is used, rather than a percentage number expression. The reason is that the wide scope interpretation of this example should be easier to perceive when the group of software engineers that Huawei wants to hire is more specific. Usually, when a percentage number expression is used, a large number of entities is involved and the identity of these entities is usually not important. Consequently, an RM phrase with a percentage number expression cannot easily receive a specific interpretation. To avoid this confound factor, I chose to use a fraction number. [^]
  6. In addition to the de re and de dicto readings discussed here, there is another scope interpretation available in an intensional environment. Briefly, the scope interpretation indicates that a proportional number expression can be further decomposed into two parts. For example, one third may contain a component denoting the fraction number 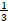, which can scopally interact with an intensional verb. In fact, this kind of scope interactions is observed in many quantity expressions (Hackl 2000; Kennedy 2015) and independent to the conservative and non-conservative readings of relative measurement. A detailed discussion is laid out in Appendix C in the supplement file. [^]
  7. According to Dotlačil & Nouwen (2016), in parallel to the pluralization of nominals, < can be pluralized as **<: if d < d″ and d′ < d″′, then d ⊔ d′** < d″ ⊔ d″′. [^]
  8. As a reviewer has remarked, division does not operate on all kinds of degrees (Krantz et al. 1971). For example, division is defined for extensive degrees on a quantitative scale, not for degrees on a non-quantitative scale like military ranking or degrees on an interval scale like temperature. [^]
  9. The proposed structure follows previous studies of quantity expressions. Positing Meas between the proportional number expression and the NP is similar to a proposal by Kayne (2005), who posits a null functional morpheme number in this position. In addition, it sides with Tang (1990), who argues that a number expression and another function item like a classifier can form a complex functional head. Moreover, following Tsai (2011), de is treated as a clitic. Independent justifications for the syntactic assumptions are not provided in this paper, Interested readers are referred to the cited studies. [^]
  10. In this paper, the capital lambda Λ is the lambda abstraction operator in the LF, which is part of the object language. It should be distinguished from λ, which is part of the meta-language. [^]
  11. Meas is not entirely new. It can actually be seen as a composition of the counting quantifier determiner assumed in Hackl (2000) and the so-called ‘point-to-interval’ operator, which is first proposed by Heim (2006) and adapted by Dotlačil & Nouwen (2016) into the theory of degree pluralities. [^]
  12. Readers may notice that the application of min is redundant in (30), because the maximum of the set of d′-s is the same as the minimum of the set of d-s. Nevertheless, Section 3.4 will show that the combination of min and max is important to explain why a degree quantifier and its trace cannot be intervened by another scope-bearing element. [^]
  13. In Figure 4, the focused NP complement could move to a specifier of a focus projection. However, the proposed derivation does not rely on any specific assumption about covert focus movement. To my knowledge, previous studies pursuing covert focus movement has not spelled out the syntactic details of such a kind of movement. Hence, the syntactic categories of the landing sites of the moved items are left open. This issue is worthy of an independent discussion in future research. [^]
  14. Note that the meaning represented in (50) is intensionalized. This paper is mainly concerned with extensional meanings. Therefore, I will not intensionalize the lexical entries defined in the paper unless they are embedded in intensional environments. [^]
  15. Notice that the type of the proportional number expression is (d → ((e → s → t) → (s → t))) → ((e → s → t) → (s → t)). s} is the type of possible worlds. In particular, is a function from degrees to intensional quantifiers of type d → ((e → s → t) → (s → t)), P is an intensional predicate of type e → s → t, and gc is an intensional predicate given in context. [^]
  16. A reviewer points out a potential problem for this account. Consider (i). Usually, we utter this sentence without knowing the exact even numbers between 1 and 10,000. It indicates that the prominent reading of (i) is the non-conservative de dicto reading. As a mathematical fact, the even numbers between 1 and 10,000 don’t vary relative to different possible worlds. As a result, the definedness condition given in (52) might be satisfied.
      1. (i)
      1. Yī
      2. one
      1. dào
      2. to
      1. yíwàn
      2. ten.thousand
      1. zhījiān
      2. between
      1. kěndìng
      2. certainly
      1. bāohán
      2. contain
      1. yíbàn
      2. half
      1. de
      2. lnk
      1. ǑUSHÙ.
      2. even.numbers
      1.  
      1. a.
      1.    Non-conservative de dicto: certainly > half even numbers
      2.    ‘For all worlds w compatible with our knowledge about the actual world w0, half of the numbers between 1 and 10,000 are even in w.’
      1.  
      1. b.
      1. ??Non-conservative de re: half even numbers > certainly
      2.    ‘There’s a maximal set X of even numbers in the actual world w0 such that, for all worlds w compatible with our knowledge about w0, X makes up half of the numbers between 1 and 10,000 in w.’
    However, the definedness condition not only disallows variation relative to possible worlds (‘for any w′’) but also variation relative to different predicates (‘for any P′’). Therefore, if a predicate of even numbers does not lead to a mathematical statement, variation would still be possible. [^]
  17. The LF presented in (53) raises a syntactic issue about the size of the clause embedded by a control verb. Theoretically, it is not clear whether or not such a clause can provide a landing site for covert focus movement, but empirically the movement approach to focus may need to assume that a focused item can covertly move within the scope of a control verb. Consider (i). The focused indefinite can receive a de dicto interpretation. It means that the covert movement of the indefinite can target a position at the edge of the embedded clause.
      1. (i)
      1. John wants to hire only a COOK.
    [^]
  18. Note that not all kinds of degree quantifiers cannot scope over intensional verbs. In fact, the comparative/superlative morpheme, which is argued to denote a degree quantifier, can scopally interact with intensional verbs (Kennedy 1997; Heim 2000; Hackl 2000; a.o.). I will return to this issue in Appendix C in the supplementary file. [^]
  19. In Mandarin, the compound of an integer and the morpheme duō ‘more’ is an approximate number expression. For example, shí-duō means a number between 10 and 20. [^]
  20. Additionally, it seems that a ‘conservative’ RM phrase does not always take narrow scope relative to another quantificational DP. Consider (i), which is a dative construction. The ‘conservative’ RM phrase occurs in the indirect object position and prefers to scope over the quantificational DP in the direct object position. This matches Takahashi’s (2006) observation in English: in a dative construction, a modified numeral in the indirect object position can scope over a quantificational DP in the direct object position.
      1. (i)
      1. Lǐbái
      2. Libai
      1. jiǎng-le
      2. sent
      1. zhěnghǎo
      2. exactly
      1. liǎng-gě
      2. two-cl
      1. gùshì
      2. stories
      1. gěi
      2. to
      1. sānfēnzhīyī
      2. one.third
      1. de
      2. lnk
      1. xuéshēng.
      2. students
      1.  
      1. a.
      1. ?Conservative: exactly two stories > one third students
      2. ‘There are exactly two stories such that Libai told both to one third of the students.’
      1.  
      1. b.
      1. Conservative: one third students > exactly two stories
      2. ‘There are one third of the students such that Libai told each of them exactly two stories.’
    It is not surprising to observe such a scopal contrast between SVO constructions and dative constructions. In Mandarin, a universal quantifier exhibits similar scopal properties: it can take inverse scope when it is used as the indirect object in a dative construction, but not when it is used as the object in a SVO construction (Huang 1982; Aoun & Li 1989; Gan & Tsai 2020; a.o.). Most of the existing studies attribute the scopal contrast to the structural distinction between an SVO construction and a dative construction, but they do not share the same syntactic assumption about dative constructions. Given that the syntactic nature of dative constructions is still debated, the present paper cannot provide a thorough analysis for the wide scope reading in (ib) at this stage. [^]
  21. As far as I am aware, Takahashi (2006) has proposed a semantic analysis to tackle this issue. Let me assume, following his analysis, that an RM phrase is decomposed into three components—a number expression, a null functional head prop and a nominal expression, as visualized in (i). See Appendix C in the supplementary file for a more detailed discussion about this decompositional analysis.
      1. (i)
      1. [DP [40%]-prop]-Meas locals]
    The percentage number expression denotes a quantifier over degrees of proportion (Solt 2018) but it takes scope over a propositional meaning. Specifically, ⟦40%⟧g = λD.max{d : D(d)} = 40%. It has the type (d → t) → t (Heim 2000; Hackl 2000; Kennedy 2015; a.o.). Therefore, the derivation of the conservative reading also involves scope taking of a degree quantifier, as shown below.
      1. (ii)
      1. [ Λ1 [[DP [-prop] Λ2 [DP t2-Meas locals]] Λ3 [s Huawei hired t3]]]
    Consequently, in an RM construction with a conservative reading, there is a degree quantifier that may interact with another scope-bearing element c-commanding the RM phrase. Returning to (54), the fraction expression one third must first take scope above the exaclty-DP to generate the wide scope reading of the RM phrase.
      1. (iii)
      1. [[one third] Λ1 [exactly two students read [[t1-prop]-Meas novels]]]
    This LF is illegitimate and ruled out because the quantificational DP cannot intervene between the degree quantifier denoted by one and its trace. As a result, the remnant of the RM phrase cannot take scope. However, this analysis under-generates. It cannot explain why a ‘conservative’ RM phrase can take scope over negation, given that a negative item is also prevented from intervening between a degree quantifier and its trace. [^]
  22. As pointed out by a reviewer, in addition to the parallel scope-taking patterns, RM phrases and modified numerals in Mandarin exhibit a structural similarity. In these two kinds of quantity expressions, the linker de can always occur between the number expressions and the NP complements, for instance, shí-duō běn de shū ‘more than 10 books’ and sānfēnzhīyī de shū ‘One third of the books’. These similarities indicate that there may be some more essential commonalities between RM phrases and modified numerals. However, de cannot intervene in all kinds of numeral expressions. As noticed in Cheng & Sybesma (1999), de is not allowed to occur between a count-classifier and an NP, such as *sān gè de rén ‘three people’. Although the distribution of de in numeral expressions is indeed significant, it is beyond the scope of this paper and is left for future research. [^]
  23. Note that the non-conservative reading in (67) would not be licensed even if the dislocated demonstrative phrase bears an accent. [^]
  24. A reviewer doubts if locating an RM phrase in a PP adjunct blocks the relevant non-conservative reading. They consider the non-conservative reading of (i) perfect.
      1. (i)
      1. Gōngsī
      2. company
      1. [gěi
      2. to
      1. 40%
      2. 40%
      1. de
      2. lnk
      1. běndì
      2. local
      1. yuángōng,
      2. employees
      1. 60%
      2. 60%
      1. de
      2. lnk
      1. fēi-běndì
      2. not-local
      1. yuángōng]
      2. employees
      1. quán
      2. all
      1. dōu
      2. dist
      1. jiā-le
      2. increase-prf
      1. xīn.
      2. salary
      1.  
      1. a.
      1. ‘The company has increased the salary for 40% of the local employees and 60% of the non-local ones.’
      1.  
      1. b.
      1. ‘60% of the people that the company has increased the salary for are local employees; 40% of the people that the company has increased the salary for are non-local employees.’
    However, my informants and I still prefer the conservative reading. The individual variation might be related to the fact that Mandarin prepositions have many verbal properties. For example, gěi can also be used as a main verb. Therefore, if a native speaker treats gěi as a verb, they would think that the RM phrase in (78) or (i) is also in a post-verbal position. [^]

Supplementary files

The supplementary file for this paper can be found as follows: https://doi.org/10.16995/glossa.5787.s1

Acknowledgements

I wish to thank Anna Szabolcsi, Lucas Champollion, Chris Barker, Simon Charlow, Uli Sauerland, Jess Law, Mingming Liu, two anonymous reviewers, and the editors Uli Sauerland and Robert Pasternak for their helpful comments and suggestions. I also thank the audiences at CLS 52 (Chicago) and SuB 22 (Edinburgh).

Funding information

This paper received support from GDUFS Research Grant 299-GK20G116.

Competing interests

The author has no competing interests to declare.

References

Ahn, Dorothy & Sauerland, Uli. 2015a. The grammar of relative measurement. In D’Antonio, Sarah & Moroney, Mary & Little, Carol Rose (eds.), Proceedings of Semantics and Linguistic Theory 25. 125–142. Stanford, CA: Stanford University. DOI:  http://doi.org/10.3765/salt.v25i0.3062

Ahn, Dorothy & Sauerland, Uli. 2015b. Non-conservative quantification with proportional quantifiers: Crosslinguistic data. In Bui, Thuy & Ozyildiz, Deniz (eds.), Proceedings of NELS 45. 1–11. Amherst, MA: GLSA.

Ahn, Dorothy & Sauerland, Uli. 2017. Measure constructions with relative measures: Towards a syntax of non-conservative construals. The Linguistic Review 34. 1–34. DOI:  http://doi.org/10.1515/tlr-2017-0001

Aoun, Joseph & Li, Audrey Yen-Hui. 1989. Scope and constituency. Linguistic Inquiry 20. 141–172.

Barker, Chris. 2007. Parasitic scope. Linguistics and Philosophy 30. 407–444. DOI:  http://doi.org/10.1007/s10988-007-9021-y

Barker, Chris. 2021. Rethinking scope islands. Linguistic Inquiry. DOI:  http://doi.org/10.1162/ling_a_00419

Barwise, John & Cooper, Robin. 1981. Generalized quantifiers and natural language. Linguistics and Philosophy 4. 159–219. DOI:  http://doi.org/10.1007/BF00350139

Beck, Sigrid. 2010. Quantifiers in than-clauses. Semantics & Pragmatics 3. 1–72. DOI:  http://doi.org/10.3765/sp.3.1

Beghelli, Filippo. 1995. The phrase structure of quantifier scope. Los Angeles: UCLA dissertation.

Beghelli, Filippo & Ben-Shalom, Dorit & Szabolcsi, Anna. 1997. Variation, distributivity, and the illusion of branching. In Ways of Scope Taking, 29–69. Kluwer Academic Press. DOI:  http://doi.org/10.1007/978-94-011-5814-5_2

Beghelli, Filippo & Stowell, Timothy. 1997. Distributivity and negation: The syntax of each and every. In Szabolcsi, Anna (ed.), Ways of taking scope, 71–107. Kluwer. DOI:  http://doi.org/10.1007/978-94-011-5814-5_3

Bumford, Dylan. 2017. Split-scope definites: Relative superlatives and haddock descriptions. Linguistics and Philosophy 40. 549–593. DOI:  http://doi.org/10.1007/s10988-017-9210-2

Cheng, Lisa Lai-Shen & Sybesma, Rint. 1999. Bare and not-so-bare nouns and the structure of NP. Linguistic Inquiry 30(4). 509–542. DOI:  http://doi.org/10.1162/002438999554192

Diesing, Molly. 1992. Indefinites. Cambridge, Massachusetts: MIT Press.

Dotlačil, Jakub & Nouwen, Rick. 2016. The comparative and degree pluralities. Natural Language Semantics 24. 45–78. DOI:  http://doi.org/10.1007/s11050-015-9119-7

Drubig, Hans Bernhard. 1994. Island constraints and the syntactic nature of focus and association with focus. Arbeitspapiere des Sonderforschungsbereichs 340.

Erlewine, Michael Y. & Kotek, Hadas. 2017. Focus association by movement: Evidence from tanglewood. Linguistic Inquiry. DOI:  http://doi.org/10.1162/ling_a_00263

Erteschik-Shir, Nomi. 1977. On the nature of island constraints: Massachusetts Institute of Technology dissertation.

Gan, Tian & Tsai, C.-Y. Edwin. 2020. The syntax of mandarin dative alternation: An argument from quantifier scope interpretation. International Journal of Chinese Linguistics 7(2). 187–222. DOI:  http://doi.org/10.1075/ijchl.20006.gan

Hackl, Martin. 2000. Comparative quantifiers: Massachusetts Institute of Technology dissertation.

Hackl, Martin. 2009. On the grammar and processing of proportional quantifiers: most versus more than half. Natural Language Semantics 17(1). 63–98. DOI:  http://doi.org/10.1007/s11050-008-9039-x

Heim, Irene. 1982. The semantics of definite and indefinite Noun Phrases: University of Massachusetts at Amherst dissertation.

Heim, Irene. 2000. Degree operators and scope. In Jackson, Brendan & Matthews, Tanya (eds.), Proceedings of SALT X, 40–64. Cornell University, Ithaca, NY: CLC Publications. DOI:  http://doi.org/10.3765/salt.v10i0.3102

Heim, Irene. 2006. Remarks on comparative clauses as generalized quantifiers. Manuscript. MIT.

Herburger, Elena. 1997. Focus and weak noun phrases. Natural Language Semantics 5(1). 53–78. DOI:  http://doi.org/10.1023/A:1008222204053

Herburger, Elena. 2000. What counts: focus and quantification. Cambridge, Massachusetts: MIT Press. DOI:  http://doi.org/10.7551/mitpress/7201.001.0001

Hsieh, I. T. Chris. 2017. The scope of reciprocal degree operators and degree pluralities. In Burgdorf, Dan & Collard, Jacob & Maspong, Sireemas & Stefánsdóttir, Brynhildur (eds.), Proceedings of Semantics and Linguistic Theory 27. 620–635. DOI:  http://doi.org/10.3765/salt.v27i0.4150

Huang, C.-T. James. 1982. Logical relations in Chinese and the theory of grammar: Massachusetts Institute of Technology dissertation.

Ioup, Georgette. 1975. The treatment of quantifier scope in a transformational grammar. New York, NY: The City University of New York dissertation.

Jin, Jing. 2015. The partitive construction in Mandarin Chinese. International Journal of Chinese Linguistics 2(1). 85–120. DOI:  http://doi.org/10.1075/ijchl.2.1.04jin

Kayne, Richard. 2005. A note on the syntax of quantity in English. In Movement and silence, 176–214. Oxford: Oxford University Press. DOI:  http://doi.org/10.1093/acprof:oso/9780195179163.003.0008

Keenan, E. L. & Stavi, Jonathan. 1986. A semantic characterization of natural language determiners. Linguistics and Philosophy 9. 253–326. DOI:  http://doi.org/10.1007/BF00630273

Kennedy, Christopher. 1997. Projecting the adjective: The syntax and semantics of gradability and comparison. Santa Cruz: University of California, Santa Cruz dissertation.

Kennedy, Christopher. 2015. A “de-Fregean” semantics (and neo-gricean pragmatics) for modified and unmodified numerals. Semantics & Pragmaticss 8. 1–44. DOI:  http://doi.org/10.3765/sp.8.10

Krantz, David H. & Luce, R. Duncan & Suppes, Patrick & Tversky, Amos. 1971. Foundations of measurement. New York and London: Academic Press. DOI:  http://doi.org/10.1016/B978-0-12-425401-5.50011-8

Krifka, Manfred. 2006. Association with focus phrases. In Molnár, V. & Winkler, Susanne (eds.), The architecture of focus, vol. 82 (Studies in Generative Grammar), 105–135. Mouton de Gruyter. DOI:  http://doi.org/10.1515/9783110922011.105

Lassiter, Daniel. 2012. Quantificational and modal interveners in degree constructions. In Chereches, Anca (ed.), Proceedings of Semantics and Linguistic Theory 22. 565–583. DOI:  http://doi.org/10.3765/salt.v22i0.2649

Lee, Thomas H.-T. 1986. Studies on quantification in chinese: University of California at Los Angeles Ph.d.

Lee, Youngjoo. 2005. Exhaustivity as Agreement: The case of Korean Man ‘only’. Natural Language Semantics 13(2). 169–200. DOI:  http://doi.org/10.1007/s11050-004-6410-4

Liu, Feng-Hsi. 1990. Scope dependency in English and Chinese. Los Angeles: University of California dissertation.

Partee, Barbara H. 1991. Topic, focus and quantification. In Moore, Steven & Wyner, Adam Zachary (eds.), Proceedings of the first semantics and linguistic theory conference, 159–188. Cornell University: Cornell University Working Papers in Linguistics. DOI:  http://doi.org/10.3765/salt.v1i0.2918

Pasternak, Robert & Sauerland, Uli. to appear. German measurement structures: Casemarking and non-conservativity. The Journal of Comparative Germanic Linguistics.

Rooth, Mats. 1985. Association with focus: University of Massachusetts at Amherst dissertation.

Rooth, Mats. 1992. A theory of focus interpretation. Natural Language Semantics 1(1). 117–121. DOI:  http://doi.org/10.1007/BF02342617

Sauerland, Uli. 1998. The meaning of chains. Cambridge, Massachusetts: Massachusetts Institute of Technology dissertation.

Sauerland, Uli. 2014. Surface non-conservatitiy in German. In Pinon, Christopher (ed.), Empirical issues in syntax and semantics, vol. 8, CSSP.

Schwarzschild, Roger. 1996. Pluralities. Dordrecht; Boston: Kluwer Academic. DOI:  http://doi.org/10.1007/978-94-017-2704-4

Solt, Stephanie. 2015. Q-adjectives and the semantics of quantity. Journal of Semantics 32. 221–273. DOI:  http://doi.org/10.1093/jos/fft018

Solt, Stephanie. 2018. Proportional comparatoves and relative scales. In Truswell, Robert & Cummins, Chris & Heycock, Caroline & Rabern, Brian & Rohde, Hannah (eds.), Proceedings Sinn und Bedeutung 21. 1123–1140. Edinburgh.

Stateva, Penka. 2004. Beck effects in the comparative. In Meier, Cécile & Weisgerber, Matthias (eds.), Proceedings of Sinn und Bedeutung 8. 283–300.

Szabolcsi, Anna. 1986. Comparative superlatives. In Fukui, Naoki & Rapoport, Tova & Sagey, Elizabeth (eds.), MIT Working Papers in Linguistics 8. 245–266.

Szabolcsi, Anna. 1997. Strategies for scope taking. In Szabolcsi, Anna (ed.), Ways of Scope Taking, 109–154. Dordrecht: Kluwer Academic Publishers. DOI:  http://doi.org/10.1007/978-94-011-5814-5_4

Szabolcsi, Anna & Zwarts, Frans. 1992. Weak islands and an algebraic semantics for scope taking. Natural Language Semantics 1(3). 235–284. DOI:  http://doi.org/10.1007/BF00263545

Takahashi, Shoichi. 2006. More than two quantifiers. Natural Language Semantics 14(1). 57–101. DOI:  http://doi.org/10.1007/s11050-005-4534-9

Tang, C.-C. Jane. 1990. Chinese phrase structure and the extended x’-theory: Cornell University dissertation.

Tomaszewicz, Barbara. 2015. Superlative ambiguities: A comparative perspective. Los Angeles, CA: University of Southern California dissertation.

Tsai, Wei-Tien Dylan. 2001. On subject specificity and theory of syntax-semnatics interface. Journal of East Asian Linguistics 10(2). 129–168. DOI:  http://doi.org/10.1023/A:1008321327978

Tsai, Wei-Tien Dylan. 2011. Rethinking formal licensing. Presented at GLOW in Asia Workshop for Young Scholars, Mie University.

von Fintel, Kai. 1994. Restrictions on quantifier domains: University of Massachusetts-Amherst dissertation.

Wagner, Michael. 2006. Association by movement: evidence from NPI-licensing. Natural Language Semantics 14(4). 297–324. DOI:  http://doi.org/10.1007/s11050-007-9005-z

Wellwood, Alexis. 2015. On the semantics of comparison across categories. Linguistics and Philosophy 38. 67–101. DOI:  http://doi.org/10.1007/s10988-015-9165-0

Westerstahl, Dag. 1985. Logical constants in quantifier languages. Linguistics and Philosophy 8. 387–413. DOI:  http://doi.org/10.1007/BF00637410

Xu, Liejiong. 1996. Limitation on subjecthood of numerically quantified noun phrases: A pragmatic approach. Ms. City University of Hong Kong.