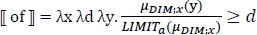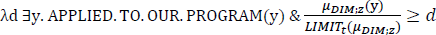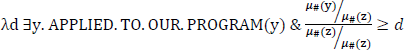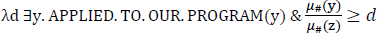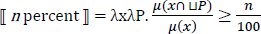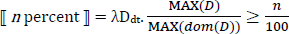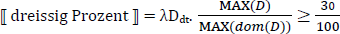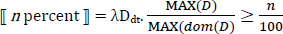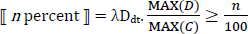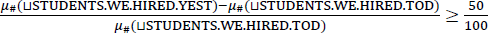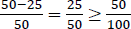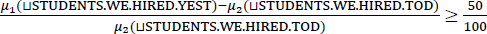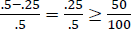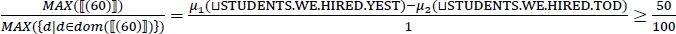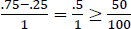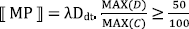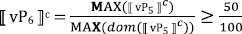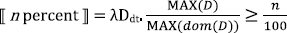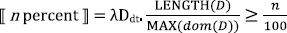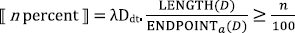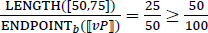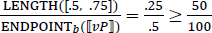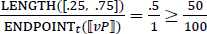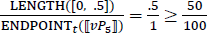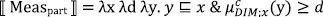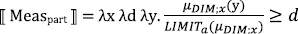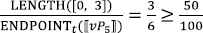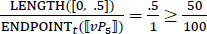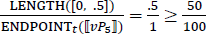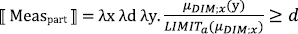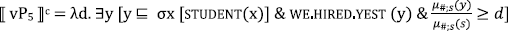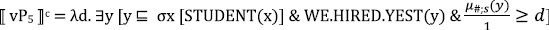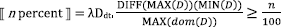1 Introduction
This paper investigates the distribution of proportional readings in nominal measurement structures in Greek. Proportional readings specify the proportional relation of two measurements. In the cases we are mostly interested in in this paper the relation is expressly specified by a percentage, i.e. a phrase of the form n percent in English or n tis ekato ‘n percent’ in Greek (where n a number). The first structure under investigation is the case of comparatives where percentages appear as differential measure phrases, as in (1). We will show that (1) is three-way ambiguous. Next to a reading in which the percentage specifies the proportional relation of two cardinalities, it also supports two additional readings in which the underlying measures are themselves proportional.
- (1)
- Exthes
- yesterday
- proslavame
- hired.1pl
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- perisoterus
- more.pl.acc
- fitites
- student.pl.acc
- apo
- from
- oti
- rel
- simera.
- today
- ‘We hired fifty percent more students yesterday than we did today.’
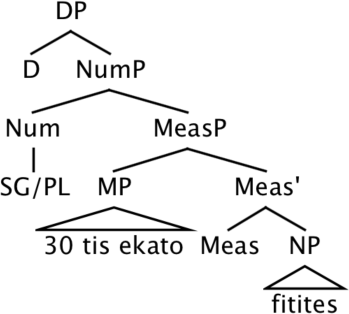
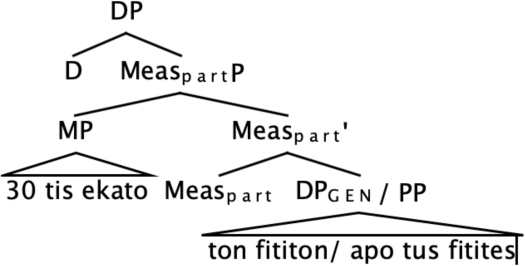
Next, we will move to juxtaposed nominal measurement structures, as in (2), and partitive measurement structures, as in (3). The structures in (2) and (3) differ on the types of proportional readings they exhibit, a difference that is morpho-syntactically conditioned. As described first for the German equivalents of (2) and (3) in Ahn & Sauerland (2015; 2017), whereas the juxtaposed structure in (2) supports a reverse proportional reading according to which the percentage specifies the proportional relation of the number of students we hired to the total number of people we hired, the partitive structure in (3) only gives rise to a forward proportional readings which specifies the proportional relation between the number of students we hired to the total number of students.
- (2)
- Exthes
- yesterday
- proslavame
- hired.1pl
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- fitites.
- students.acc
- ‘Thirty percent of the people we hired yesterday were students.’
- (3)
- Exthes
- yesterday
- proslavame
- hired.1pl
- (to)
- the
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- ton
- the.gen
- fititon /
- students.gen
- apo
- from
- tus
- the
- fitites.
- students.acc
- ‘We hired thirty percent of the students yesterday.’
This paper asks the question to what extent it is possible to unify the analyses of not only the data in (1)–(3), but also with structures that do not contain proportional modifiers like percentages. The crucial ingredient of the analyses we consider pertains to the locus of proportionality in the grammar of nominal measurement structures. An obvious candidate for the locus of proportionality in (1)–(3) is the percentage itself. Indeed, Ahn & Sauerland (2015; 2017) and, more recently, Pasternak and Sauerland (2022) propose analyses of juxtaposed and partitive structures in which proportionality only comes into play via the meaning of the proportional modifier. Based on recent work in Solt (2018), Bale & Schwarz (2020), and Bale (2022), we argue that the best candidate for a unified analysis of proportionality in nominal measurement is a proportional μ-based analysis, i.e. an analysis that (also) locates proportionality in the specification of the underlying measures. We argue that differential comparatives like (1) provide novel evidence for the necessity of such an analysis and extend this type of analysis to juxtaposed and partitive structures. The need for such a reanalysis of juxtaposed and partitive structures does not only stem from a desire for analytical parsimony, however. Next to other considerations, we show that the availability of reverse proportional readings correlates with the availability of some of the readings of the corresponding differential comparatives, a correlation that follows naturally if proportionality in the two structures has the same origin (i.e. is located in the measures themselves) and the typology of proportional measure functions is taken into consideration. We notice, however, that our first attempt at such an analysis leads to an over-generation problem. We argue that the cause of this problem does not lie with the proportional μ-based analysis, but rather with the entry for percentages we have been assuming to this point. We propose a modification of the analysis of differential comparatives that solves the overgeneration problem, captures the observed correlation between readings, and allows us to assume a single entry for proportional modifiers in all cases.
The paper is organized as follows. Section 2 presents an overview of existing literature on proportionality in the nominal domain. Section 3 presents the different readings of percentages in differential comparatives and proposes an analysis based on proportional measure functions. Section 4 presents Greek juxtaposed measurement structures and proposes an analysis in terms of proportional measure functions. Section 5 does the same for partitive measurement structures. Section 6 concludes.
2 Proportionality in the nominal domain
This section presents a short excursion of the literature on proportionality in nominal measurement structures. We do not aim to provide an exhaustive overview of all relevant data and the analyses that have been proposed. Rather, we focus on the data that are more directly linked to the cases that are the main interest of the paper. In doing so, we present (a) the available analytical options as it pertains to the locus of proportionality in the grammar of nominal measurement, (b) the basic ingredients that any analysis must include, and (c) the existing alternatives that we pitch our own analysis against.
2.1 Forward and reverse proportionality
Proportional readings in the nominal domain have mainly been discussed in the literature on the basis of examples with many and few. It is known since at least Westerståhl (1985a) that next to a cardinal reading, as in, e.g., (4a) (Partee 1989), which requires that the cardinality of the faculty children who attended the party is below a contextually determined standard, few (and many) can give rise to a proportional reading, as in, e.g., (4b) (Partee 1989), according to which the ratio of the cardinality of egg-laying mammals who suckle their young to the cardinality of all egg-laying mammals is below a contextually determined standard. Next to this forward proportional reading, however, proportional uses are also known to give rise to a reverse proportional reading (Westerståhl 1985b), as in, e.g., (4c) (Herburger 1997) according to which the proportion of the cardinality of cooks who applied to the cardinality of all applicants lies below a contextual standard.
- (4)
- a.
- b.
- c.
- There were few faculty children at the 1980 picnic.
- Few egg-laying mammals suckle their young.
- Few cooks applied.
- cardinal
- forward proportional
- reverse proportional
The simplest way to capture the various uses of few/many is to assume a three-way lexical ambiguity, as in (5) and (6), where n is a contextually determined cardinality and p a contextually determined proportion. The difference between forward and reverse proportional readings, then, depends on whether it is the restrictor or the scope of few/many that appears in the denominator of the fraction.
- (5)
- a.
- ⟦ fewCARD ⟧ = λRet λSet. |R ∩S| < n
- b.
- ⟦ fewF_PROP ⟧ = λRet λSet. |R ∩S|⁄|R|< p
- c.
- ⟦ fewR_PROP ⟧ = λRet λSet. |R ∩S|⁄|S|< p
- (6)
- a.
- ⟦ manyCARD ⟧ = λRet λSet. |R ∩S| > n
- b.
- ⟦ manyF_PROP ⟧ = λRet λSet. |R ∩S|⁄|R|> p
- c.
- ⟦ manyR_PROP ⟧ = λRet λSet. |R ∩S|⁄|S|> p
Many attempts have been made to reduce the number of entries and avoid lexical ambiguity as much as possible. Such analyses have particularly focused on deriving reverse proportional readings on the basis of manyCARD/fewCARD or manyF_PROP/fewF_PROP, since the entries in (5c) and (6c) seems to be counterexamples to the Conservativity Hypothesis of Keenan & Stavi (1986). One strategy that has been used to that effect is to drop the assumption that the locus of proportionality is the quantifier itself and assume that (reverse) proportionality is the result of manipulating the contextual standard. As pointed out by Westerståhl (1985b) (cf. Bale & Schwarz 2020) proportional readings can then be derived on the basis of the cardinal entries in (5a)/(6a) as shown in (7) and (8).
- (7)
- a.
- ⟦ few ⟧ = λRet λSet. |R ∩S|< n where n ≔ p × |R|
- b.
- ⟦ few ⟧ = λRet λSet. |R ∩S|< n where n ≔ p × |S|
- (8)
- a.
- ⟦ many ⟧ = λRet λSet. |R ∩S|> n where n ≔ p × |R|
- b.
- ⟦ many ⟧ = λRet λSet. |R ∩S|> n where n ≔ p × |S|
Another possibility has recently been proposed in Bale & Schwarz (2020), one that places proportionality in the meaning of measure functions. In degree semantics, the job of relating individuals to their measurement in some dimension is done by measure functions (Cresswell 1976; von Stechow 1984; a.o.), which map entities in the domain of individuals to degrees in some dimension of measurement DIM. The entries for few/many can be rewritten as in (9), where the measure function μ measures the supremum of the intersection of the two sets in some dimension of measurement. Crucially, the value of the measure function is not constant, but is rather determined by context. In the case of cardinal readings, the function measures cardinality, i.e. it counts the number of atoms in a given set by counting the atomic parts of the supremum of the set.
- (9)
- a.
- ⟦ few ⟧c = λd λRet λSet. μc(⊔ (R ∩S) ≤ d
- b.
- ⟦ many ⟧c = λd λRet λSet. μc(⊔(R ∩S) ≥ d
- (10)
- μ = λx. |x|
To derive proportional readings, proportionality is built in the measure function itself (cf. Solt 2018). Degrees in the scope of a proportional measure function represent the ratio of two measurements, as in (11) (Bale 2022, based on Bale & Schwarz 2020).1,2 The measured individual in the numerator is always the argument of the measure function.
- (11)
- Given a non-proportional measure μ that maps a domain E into the dimension DIM, and given a contextually determined degree d* that is a member of DIM, there is an associated proportional measure such that for any .
Forward and reverse readings differ on what is measured in the denominator. The forward proportional reading of (4b) is derived by setting the degree d*to the cardinality of the sum of egg-laying mammals, as in (12a), and the reverse proportional reading of (4c) by setting the degree d*to the cardinality of the sum of applicants, as in (12b).3
- (12)
- a.
- μ = λx. |x|⁄|⊔ EGG-LAYING.MAMMALS|
- b.
- μ = λx. |x|⁄|⊔ APPLICANTS|
As Bale & Schwarz’s (2020) show the account can be straightforwardly extended to proportional readings of other measurement constructions, as in, e.g., proportional readings in comparatives. For example, (13) has a proportional reading according to which what is compared are two proportions; the proportion of the number of cooks that applied to our program to the total number of applicants in our program and the proportion of the number of cooks that applied to your program to the total number of applicants in your program.4
- (13)
- More cooks applied to our program than to yours.
Since the comparative obviously does not have a standard-related interpretation, an analysis along the lines of (7)/(8) is unavailable. Whereas (13) can be analyzed using both a lexical analysis along the lines of (5)/(6), or an analysis based on proportional measure functions, Bale & Schwarz (2020) use examples like (14) in order to exclude a lexical analysis. Next to a cardinal reading, (14), also supports a reading in which what is compared is the density of road signs in the two routes. If so, (14) can be true even if the number of road signs on Rte 101 is less than the number of road signs on Rte 104.
- (14)
- There are more road signs on Rte 101 than on Rte 104.
Bale & Schwarz (2020) propose to capture this reading by means of the proportional measure functions in (15), where the value in the denominators represent the number of miles that constitute the length of the two routes. The crucial point here is that the degrees in the denominators in (15) are not retrievable from the sentence in (14), excluding a lexical analysis. An analysis in terms of proportional measure functions is thus shown to be independently necessary and can be extended to (13), assuming that the relevant proportional measures are as in (16).
- (15)
- a.
- μ1 = λx. |x|⁄|MILES.OF.RTE.101|
- b.
- μ2 = λx. |x|⁄|MILES.OF.RTE.104|
- (16)
- a.
- μ1 = λx. |x|⁄|APPLICANTS.TO.OUR.PROGRAM|
- b.
- μ2 = λx. |x|⁄|APPLICANTS.TO.YOUR.PROGRAM|
As discussed initially in Solt (2018), an analysis in terms of proportional measure functions can also be extended to capture known differences between the proportional readings generated by different nominal measurement structures. As known since at least Partee (1989), the presence of partitive of affects the available readings. Consider, for example, the examples in (17), which, as Bale & Schwarz (2020) and Bale (2022) show, lack the proportional reading available in (13) and (14). As discussed above, e.g., (13) can give rise to a proportional reading which measures the proportion of cooks that applied to the total number of applicants. With the addition of partitive of in (17a), however, this reading disappears. The only available reading is what we will call a partitive proportional reading, which measures the proportion of cooks that applied to the sum of some plurality of cooks. Similarly, in (17b), the comparative can only be taken to compare the number of the road signs on the two routes, not their density.
- (17)
- a.
- More of the cooks applied to our program than to yours.
- b.
- More of the road signs appear on Rte 101 than on Rte 104.
One might think that to derive the available readings of (17), it is enough that partitive of introduces the an underspecified measure function and requires that the measured entity is a sub-aggregate of the denotation of its nominal complement, as in (18). This entry is, indeed, capable of deriving readings with simple non-proportional measures, like cardinality. The problem, however, is that non-partitive proportional readings can sneak in if the measure function in (18) is resolved to proportional measure functions like the ones in (15) and (16).
- (18)
- ⟦ of ⟧ = λx λd λy. y ≤ x & μc (y) ≥ d
To solve this issue, Bale (2022), building on Solt (2018), proposes that a key ingredient in deriving the distribution of readings is to assume that partitivity is encoded in the measure function itself. This is achieved by restricting partitive measurement to domain-restricted measure functions, defined in (19) (Bale 2022: (12), based on Solt 2018). This ensures that the measure functions in partitives will have a maximum degree in their range, which is equal to the measure of the nominal complement in the relevant dimension.
- (19)
- For all entities x and y, all measure functions μ, and all dimensions DIM, μDIM;x is defined if and only if y ≤ x. When defined, μDIM;x(y) = μDIM(y) (i.e., the same value as the unrestricted version of the measure function).
The key step in eliminating the effects of proportional measure functions is to furthermore assume that partitive of also encodes a type of proportionality, as in (20) (Bale 2022: (14)). Partitives encode the proportion of the degree of the measured individual to the maximum or minimum degree in the range of the relevant measure function. LIMITa is function from measure functions to degrees that can be set to either LIMITt, in which case it returns the greatest degree in the range of measure function, or to LIMITb, in which case it returns the least degree in the range of the measure function.
- (20)
As Bale (2022) shows this entry nullifies the effects of proportional measure functions. It would take us to far to show this for every possible combination of measure function and LIMIT function. To illustrate, consider the main clause in example (17a), assuming that μ is resolved to the function in (16a) and the LIMIT function is set to LIMITt.5 If so, the degree predicate denoted by the main clause of the comparative in (17a) is the one in (21), where z the applicants to our program.
- (21)
The measure in the denominator is only defined if the cooks who applied to our program are a sub-aggregate of the applicants, which is true. By the definition of domain-restricted functions, this measure is equivalent to the non-restricted measure μDIM(y). Given the choice of proportional measure, this measure equals . Moving to the denominator, LIMITt returns the maximum degree in the range of μDIM;z. Since we are dealing with a restricted function, this is equal to μDIM;z(z), which, in turn, given the choice of proportional measure function, is equal to . (21) can thus be rewritten as in (22).
- (22)
By factoring out the denominator values, (22) is equivalent to (23), which is nothing more than a regular partitive proportional meaning based on a non-proportional measure. Bale (2022) shows how this result generalizes to all proportional measure functions.
- (23)
What we have seen so far is that there exist, in principle, at least three possible analytical options when it comes to the grammar of proportionality and its interaction with the grammar of measurement. One possibility is to locate proportionality in the meaning of a certain functional element, the same one that also introduces measurement. We will refer to this as a lexical analysis. A second option, available for at least examples with standard-related interpretations, is to introduce proportionality by manipulating a contextual standard in a certain way. We will refer to this as a standard-based analysis. The third option, the one argued in Bale & Schwarz (2020) to be able to be extended in all cases discussed here, is to link proportionality not simply with the functional element introducing measures, but with the measures themselves; whereas the meaning of the measure-introducing functional element remains constant, proportional readings are available because the measures themselves can be proportional. We will refer to this as a proportional μ-based analysis.
2.2 Proportionality with percentages
More recently proportional readings have also been discussed on the basis of nominal measurement structures with relative modifiers. Ahn & Sauerland (2015, 2017) identify another case of a reverse proportional reading in cases with explicitly relative/proportional modifiers like percentages. The German example in (24) receives a reverse proportional reading according to which the proportion of students who work here to the total number of workers equals thirty percent. The availability of the reading is morpho-syntactically conditioned. Whereas reverse proportionality is available with the juxtaposed nominal structure in (24), it is not available with the proper partitive in (25). The example in (25) can only give rise to a forward/partitive proportional reading.
- (24)
- Dreißig
- thirty
- Prozent
- percent
- Studierende
- students.nom
- arbeiten
- work
- hier.
- here
- ‘Thirty percent of the workers here are students.’
- (25)
- Dreißig
- thirty
- Prozent
- percent
- der
- the.gen
- Studierenden
- students.gen
- arbeiten
- work
- hier.
- here
- ‘Thirty percent of the students work here.’
Ahn & Sauerland provide an account of these cases that places proportionality solely in the meaning of the relative modifier, as in (26). The difference between (24) and (25) is driven by the different syntax of the relevant measurement constructions and independent properties of the relevant measurement constructions. In the most recent and more thorough investigation of these data, Pasternak & Sauerland (2022), treat the relative modifier n percent as a degree quantifier, as in (27). Whereas MAX(D) returns the maximal degree for which the degree predicate is true, MAX(dom(D)) returns the maximal degree for which the predicate returns a defined value (true or false).6
- (26)
- (27)
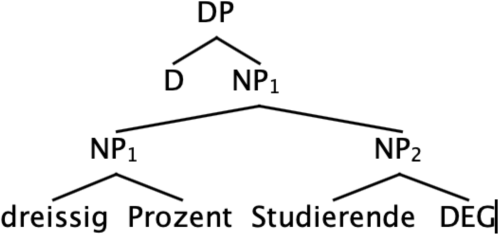
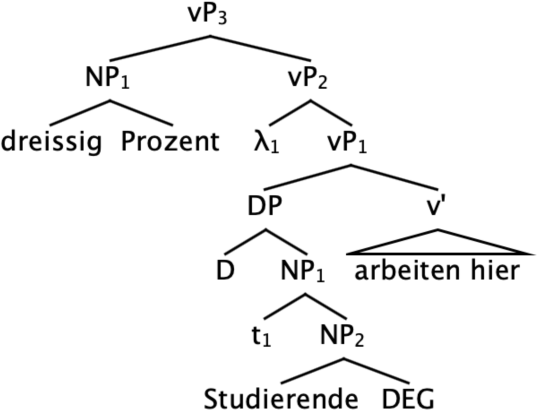
Importantly for current purposes, the modifier is the only place where proportionality comes into place in these analyses. We will refer to this type of analysis as a modifier-based analysis. Let us briefly present the modifier-based analysis of Pasternak & Sauerland (2022). We start with what Pasternak & Sauerland (2022) calls the juxtaposed structure in (24), for which they assume the syntactic structure in (28). As in much relevant literature (starting with Schwarzschild 2006), a functional element, here DEG, is taken to be responsible for combining bare nominals with degree heads, by introducing an underspecified measure function. The determiner that heads the DP is interpreted as an existential quantifier. The assumption throughout is that μc is resolved to the cardinality function.
- (28)
- (29)
- ⟦ DEG ⟧c = λPet λd λx. P(x) & μc(x) ≥ d
- (30)
- ⟦ NP2 ⟧c = λd λx. STUDENTS(x) & μc(x) ≥ d
- (31)
- (32)
- ⟦ ∃ ⟧c = λPet λQet. ∃x [P(x) & Q(x)]
To resolve the type-mismatch between the meanings of NP1 and NP2, NP1 undergoes Quantifier Raising, as in (33). The percentage now composes with the degree predicate in (34). But this raises a different problem, since MAX(dom(D)) is not defined for this predicate, since there is no maximal degree of cardinality.
- (33)
- (34)
- ⟦ vP2 ⟧c = λd ∃x. STUDENTS.WHO.WORK.HERE(x) & μc(x) ≥ d
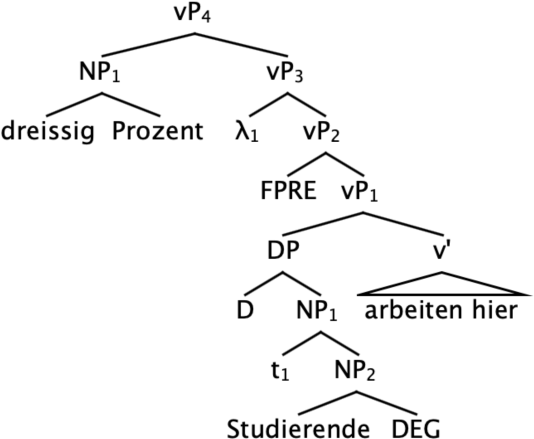
This is where focus comes in. Assuming that NP1 is focused, simultaneously achieves two things: (a) MAX(dom(D)) is now defined due to the presuppositions introduced by focus, and (b) MAX(dom(D)) returns exactly the right degree required to get a reverse proportional reading; i.e. the cardinality of the individuals who work here. While focus on NP1 retains the same ordinary interpretation in (34), it generates the focus semantic value in (36), where P ranges over predicates of individuals. Focus is also taken to introduce the presupposition that at least one of the focus alternatives is true. This presupposition is introduced by the head FPRE, which presupposes the truth of the grand disjunction of the focus value of the propositional constituent it attaches to, as in (37) (Pasternak & Sauerland 2022: (85), based on Abusch 2010). Assuming that among the alternatives to StudierendeF is a very weak predicate which is vacuously true (like human or animate), the presupposition of the degree predicate vP3 is as in (38) (introduced as a definedness condition). This presupposition renders MAX(dom(D)) defined, since the maximal degree for which the degree predicate is defined will be the cardinality of the individuals who work here. Feeding this predicate to the percentage will generate the required reading, since it will equate the ratio of the cardinality of students who work here to the cardinality of people who work here to thirty percent.
- (35)
- (36)
- ⟦ vP3 ⟧F = { λd ∃x. P(x) & WORK.HERE(x) & μc(x) ≥ d }
- (37)
- ⟦ FPRE X ⟧ is defined only if ⋁⟦ X ⟧F is true.
- Where defined, ⟦ FPRE X ⟧ = ⟦ X ⟧.
- (38)
- ⟦ vP2 ⟧c = λd: ∃x. INDIVIDUAL(x) & WORK.HERE(x) & μc(x) ≥
- d. ∃x. STUDENTS(x) & WORK.HERE(x) & μc(x) ≥ d
Notice that in this analysis focus is necessary to generate the right reading. Pasternak & Sauerland (2022) claim that this is an empirically desirable result. Not only is focus on NP1 claimed to be necessary to generate the reverse proportional reading in German, but different focus structures are claimed to have truth-conditional effects. So, whereas the sentence in (39), with broad focus on NP has the same reading as (24) (with the addition of the contribution of westfälische in the ordinary meaning), narrow focus on the adjective, as in (40), affects the value of the denominator.
- (39)
- Dreißig
- thirty
- Prozent
- percent
- [westfälische
- westphalian.nom
- Studierende]F
- students.nom
- arbeiten
- work
- hier.
- here
- ‘Thirty percent of the workers here are Westphalian students.’
- (40)
- Dreißig
- thirty
- Prozent
- percent
- [westfälische]F
- westphalian.nom
- Studierende
- students.nom
- arbeiten
- work
- hier.
- here
- ‘Thirty percent of the students who work here are Westphalian.’
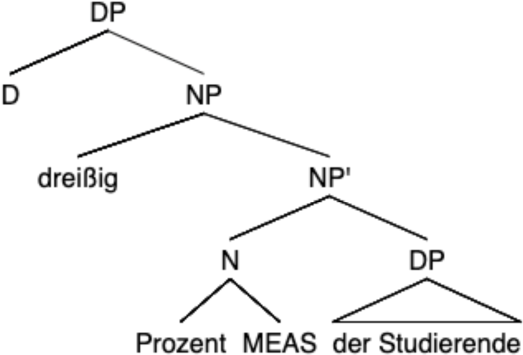
We move next, briefly, to what Pasternak and Sauerland call the genitive structure in (25), which is assigned the syntactic structure in (41). The structure is essentially treated as a partitive, with the quirk that Pasternak & Sauerland prefer having the relevant partitive functional head shift the interpretation of Prozent from a quantifier over degrees to something that measures individuals. The key component of the meaning of MEAS for current purposes is that it requires (a) the measured individual to be a sub-aggregate of the denotation of the nominal complement of Prozent MEAS and (b) the relevant measure function to be domain-restricted.7 This will ensure that MAX(dom(D)) is the cardinality of the plurality of the students as required (assuming again that μ is resolved to the cardinality function).
- (41)
- (42)
- ⟦ MEAS ⟧c = λMdt,t λx λn λy. y ≤ x & M(n)( )
- where μx[y] = λd: μ(x) ≥ d. μ(y) ≥ d
- (43)
- ⟦ Prozent MEAS ⟧c=λx λn λy. y ≤ x & MAX( )⁄MAX(dom( )) ≥ n⁄100
- = λx λn λy. y ≤ x & μc(y)⁄μc(x) ≥ n⁄100
As we have just seen a key component of existing analyses is to explain differences in the distribution of available proportional readings to the properties of different nominal structures. Particularly, partitives are taken to restrict the range of available proportional readings by imposing some additional restrictions. At the same time, however, seemingly very similar readings (the reverse proportional reading of many, the proportional reading of comparatives like (13) and the reverse proportional reading of juxtaposed structures with percentages) have been analyzed in very different ways, at least regarding the key question of the locus of proportionality in nominal measurement. The rest of this paper discusses to what extent these facts can be given a unified explanation by exploring how prima facie proportional modifiers like percentages interact with other potential sources of proportionality. Notice that a proportional analysis of percentages can, in principle, be combined with any one of the other analyses we have seen so far, multiplying the available analytical options. In this paper we will focus on two empirical domains. First, we look at a case, which, as far we know, has not been investigated before, the use of percentages in differential comparatives. Next, we move to the Greek equivalents of the German facts in (24) and (25). Since the structures we are primarily interested in are not sensitive to contextual standards, standards-based analyses will not be discussed any further. Lexical analyses will also not feature prominently in what follows, since Bale & Schwarz (2020) have already shown that they cannot capture the full range of available proportional readings, as discussed above. Our attention, thus, will focus on how the proportional measure functions of proportional μ-based analyses interact with proportional modifiers like percentages.
For the remainder of this paper, we change the language of investigation from English and German to Greek. By focusing on the Greek facts, we are not only expanding the relevant empirical landscape, but we also motivate a revision of the analysis in Pasternak & Sauerland (2022), particularly in the syntactic structures assumed for juxtaposed and partitive structures and the reliance to focus to generate reverse proportional readings. Before we move to this point, we will first consider the case of comparatives in some more detail. We argue that to account for the full range of available readings of percentages acting as differential measure phrases, a proportional μ-based analysis is necessary, even in the presence of a proportional modifier.
3 Percentages in differential comparatives
This section provides an analysis of percentages in comparatives, as in (44). Comparatives with percentages as differential measure phrases are three-way ambiguous, as they can be true in all the contexts in (44a–c). We will call the reading that makes (44) true in Context A, a relative cardinal reading, the reading that makes (44) true in Context B, a relative proportional reading, and the reading that makes (44) true in Context C, an absolute proportional reading.
- (44)
- Exthes
- yesterday
- proslavame
- hired.1pl
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- perisoterus
- more.pl.acc
- fitites
- student.pl.acc
- apo
- from
- oti
- rel
- simera.
- today
- ‘We hired fifty percent more students yesterday than we did today.’
- a.
- Context A: We hired 75 students yesterday and 50 students today.
- b.
- Context B: We hired 75 students out of 100 hirees yesterday (i.e.75%) and 100 students out of 200 hirees today (i.e. 50%).
- c.
- Context C: We hired 75 students out of 100 hirees yesterday (i.e.75%) and 100 students out of 400 hirees today (i.e. 25%).
We argue that all three readings necessitate a revision of the entry for n percent in (27) and that relative and absolute proportional readings require a proportional μ-based analysis. To account for the distribution of absolute proportional readings, we make use of a crucial distinction between proportional measure functions, domain-restricted proportional measure functions, as in Solt (2018), and non-restricted proportional measure functions. We first discuss differential comparatives with absolute differential measure phrases to present our basic assumptions about the interpretation of differential comparatives, and then move to discuss each of the readings of (44) in return turn.
3.1 Differential comparatives
Consider first a regular differential comparative as in (45).8 (45) is true in a context in which we hired 10 students yesterday and 7 today.
- (45)
- Exthes
- yesterday
- proslavame
- hired.1pl
- tris
- three
- perisoterus
- more.pl.acc
- fitites
- student.pl.acc
- apo
- from
- oti
- rel
- simera.
- today
- ‘We hired three more students yesterday than we did today.’
Following Alexiadou et al. (2021), we adopt a decompositional analysis of Greek comparatives according to which perisoteri ‘more’ is decomposed into the comparative morpheme -ter- ‘-er’ and periso- ‘many’.9 The comparative specifies a relation between sets of degrees, as in (46). We choose the variable names T and M to stand as mnemonics for ‘than-clause’ and ‘main-clause’, respectively. periso- ‘many’ introduces a measure function as in (47). In this case, the function measures cardinality, cf. Makri (2018; 2020).
- (46)
- ⟦ -ter- ⟧c = λd λTdt λMdt. MAX(M) = d + MAX(T)
- (47)
- ⟦ periso- ⟧c = λd λRet λSet. μc(⊔ (R ∩S) ≥ d
The than-clause and the main clause provide the two relevant sets of degrees, after predicate abstraction in the than-clause and after Quantifier Raising (Heim & Kratzer 1998) the degree phrase formed by the comparative morpheme and the than-clause, as in (48). The numeral tris ‘three’, which we take to name an individual degree in a scale of cardinality, provides the differential argument.
- (48)
- [[[tris -ter-]
- λd [ simera proslavame d-periso- fitites ]]
- λd [ exthes proslavame d-periso- fitites ]]
The meaning of (45) comes out as in (49), i.e. it is true if the number of students we hired yesterday exceeds the number of students we hired today by three. The differential measure phrase then simply specifies the difference between two degrees.
- (49)
- ⟦ (42) ⟧c = MAX(λd. ∃x[STUDENTS.WE.HIRED.YEST(x) & μ#(x) ≥ d])
- = 3 + MAX(λd. ∃x[STUDENTS.WE.HIRED.YEST(x) & μ#(x) ≥ d])
3.2 Differential comparatives with percentages
With this background we can now proceed to consider comparatives with percentages as differential measure phrases, repeated in (50). We observe that such examples are three-way ambiguous. In its first and most prominent reading, which we called the relative cardinal reading, the differential measure phrase represents the ratio of the difference between two cardinalities to the cardinality provided by the than-clause. Under this interpretation, (50) says that the positive difference between the number of people we hired yesterday and today equals 50 percent of the people we hired today. (50) is thus true in the context of (51a). In its second reading, which we called the relative proportional reading, (50) receives a proportional interpretation like the one discussed for (13) above. It compares the proportion of students we hired today (relative to today’s hirees) to the proportion of students we hired yesterday (relative to yesterday’s hirees). The differential measure phrase, in this case, represents the ratio of the difference between two proportions to the proportion provided by the than-clause. Under this interpretation, (50) says that the positive difference between the proportion of students we hired yesterday and today equals 50 percent of the proportion of students we hired today. (50) is thus true in the context of (51b). The third reading, which we called the absolute proportional reading, is also based on the same underlying proportional reading. In this case, however, the percentage appears to behave more like a regular, non-proportional differential measure phrase; it does not represent a ratio, but simply the difference between two proportions. Under this interpretation, (50) says that the positive difference between the proportion of students we hired yesterday and today equals 50 percent and is, thus, true in the context of (51c).10
- (50)
- Exthes
- yesterday
- proslavame
- hired.1pl
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- perisoterus
- more.pl.acc
- fitites
- student.pl.acc
- apo
- from
- oti
- rel
- simera.
- today
- ‘We hired fifty percent more students yesterday than we did today.’
- (51)
- a.
- Context A: We hired 75 students yesterday and 50 students today.
- b.
- Context B: We hired 75 students out of 100 hirees yesterday (i.e.75%) and 100 students out of 200 hirees today (i.e. 50%).
- c.
- Context C: We hired 75 students out of 100 hirees yesterday (i.e.75%) and 100 students out of 400 hirees today (i.e. 25%).
3.2.1. The relative cardinal reading
We begin by considering an analysis that deviates minimally from the analysis of differential comparatives in the previous section; i.e. we assume that the percentage functions as a regular differential measure phrase and that the LF of (50) is identical to that of other differential comparatives, as in (52). Assuming a quantificational analysis of percentages as in Pasternak & Sauerland’s entry in (27), repeated here in (53), the percentage undergoes Quantifier Raising, interpreted here in the usual way.
- (52)
- [ [peninta tis ekato] [ λ1 [[ [t1 -ter-] [ λd [ simera proslavame d-periso- fitites ]] ]
- [ λd [ exthes proslavame d-periso- fitites ]] ]] ]
- (53)
Informally, the relative cardinal reading of (50) should represent the ratio in (54). But as is immediately obvious, whereas the degree predicate in the numerator correctly represents the difference between the two cardinalities, as required, the denominator is not the maximal degree in the domain of this degree predicate (there is no such degree), but the cardinality provided by the than-clause. The entry in (53), then, needs to be revised.
- (54)
As a first attempt (to be revised in section 4.3.2), we will assume the quantificational entry in (55). (55) replaces MAX(dom(D)) in the denominator with the maximal degree of a contextually supplied predicate of degrees, MAX(C). If so, context sensitivity is introduced in two places, the variable over measure functions in the meaning of periso ‘many’ and the variable C over sets of degrees in the meaning of the percentage. The different readings of (50) will be generated by different choices in the resolution of these variables.
- (55)
The cardinal reading is generated when μ is resolved to the function measuring cardinality and C to the set of degrees introduced by the than-clause. We end up with the meaning in (56), which is verified for the context in (51a) in (57).
- (56)
- (57)
3.2.2 The relative proportional reading
The relative proportional reading can be accounted for by resolving the measure functions to proportional measure functions, as in (58). Crucially in this case, the variables over measure functions in the main clause and than-clause are resolved to different functions. If, as in the relative cardinal reading, C is resolved to the degree predicate provided by the than-clause, we end up with the meaning in (59). This correctly predicts that (50) is true in the context of (51b), as verified in (60).
- (58)
- a.
- μ1 = λx. |x|⁄|⊔ HIREES.YEST|
- b.
- μ2 =λx. |x|⁄|⊔HIREES.TOD|
- (59)
- (60)
3.2.3. The absolute proportional reading
Finally, we turn to the absolute proportional reading. In this case the percentage appears to act more like absolute measure phrases and simply specify the difference between two proportional degrees. The issue here is that, given the ingredients we have specified so far (the predicates of degrees provided by the main and the than-clauses and the measure functions in (58)), there is no obvious choice for the variable C that would give us the right result. In fact, what we need to achieve is to nullify the effects of the percentage itself, as in (61); i.e. give substance to the underlying intuition that the percentage in this case specifies a degree in the domain of the relevant proportional measure functions.11
- (61)
- μ1(⊔ STUDENTS.WE.HIRED.YEST) – μ2 (⊔ STUDENTS.WE.HIRED.TOD) ≥ 50%
To achieve this we claim that the measure functions relevant for the absolute (and relevant) proportional reading are not the ones in (58), but the domain-restricted versions of them in (62).
- (62)
- a.
- μ1 = λx :x ⊑ ⊔ HIREES.YEST. |x|⁄|⊔ HIREES.YEST|
- b.
- μ2 = λx :x ⊑ ⊔ HIREES.TOD. |x|⁄|⊔ HIREES.TOD|
The crucial difference between the functions in (58) and the ones in (62) is that only the latter have a maximal degree in their range, the degree whose value is and , namely 1. The degree predicate that composes with the percentage, which we will call the differential predicate, is given in (63).
- (63)
- λd. d = μ1 (⊔ STUDENTS.WE.HIRED.YEST)-μ2 (⊔ STUDENTS.WE.HIRED.TOD)
Assuming, as in our Context C, that we hired 75% students yesterday and 25% students today, the predicate in (63) will contain the unique degree that corresponds to the difference between the two proportions, namely 0.5. Crucially, since we are dealing with degrees of domain-restricted proportionality, the maximal degree in the domain of the differential predicate is the maximal degree in a scale of domain-restricted proportionality, namely 1. If so, the result of applying the differential predicate to the percentage and resolving the variable C to the set of degrees in the domain of (63), as in (64), is (65), the correct result.
- (64)
- C = {d|d ∈dom(⟦(60)⟧)}
- (65)
- (66)
More generally, the analysis predicts that only domain-restricted proportional measure functions will give rise to absolute proportional readings. Solt (2018) is the first work to define such functions. Like non-proportional domain-restricted functions, they are restricted to only measure parts of an individual and return degrees that encode the proportion they represent of the totality in some dimension of measurement, as in the definition in (67) (Bale 2022: (8), based on Solt 2018).12 The measure functions in (62) are domain-restricted measures based on cardinality measures whose restrictions are the sum of people we hired yesterday and today, respectively.
- (67)
- For any measure function μ into a non-proportional dimension DIM and for any restriction x, there is a domain-restricted proportional measure associated with μ, symbolized as μDIM%;x, such that for any y in the domain of , which is equal to if y ≤ x.
Importantly not all the proportional measures we have seen so far can be re-written as domain-restricted measures.13 Consider, for example, the comparative in (68), whose intended reading is based on the functions in (69), so that (65) compares the density of road signs on the two Routes. There exists no domain-restricted version of the functions in (69), as any such functions would necessarily measure miles in the numerator, not road signs, as required.
- (68)
- There are more road signs on Rte 101 than on Rte 104.
- (69)
- a.
- μ1 = λx. |x|⁄|miles of Rte 101|
- b.
- μ2 = λx. |x|⁄|miles of Rte 101|
The analysis correctly predicts then that differential percentages will not give rise to absolute proportional readings in this case, since the functions in (69) do not have maximal degrees in their range (and the corresponding predicates of degrees have no maximal degrees in their domains). Indeed, (70) is felicitous in the contexts A and B in (71), but not in context C (or any other context).
- (70)
- Afti
- this
- i
- the
- leoforos
- highway
- exi
- has.3sg
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- perisotera
- more.pl.acc
- simata
- road.sign.pl.acc
- apo
- from
- ekini.
- that
- ‘This highway has 50 percent more road signs than that one.’
- (71)
- a.
- Context A: There are 75 road signs in this highway and 50 in that one.
- b.
- Context B: There are 75 road signs per mile in this highway and 50 road signs per mile in that one.
- c.
- Context C: There are 75 road signs per mile in this highway and 25 road signs per mile in that one.
Before moving on let us briefly discuss an alternative to our analysis of absolute proportional readings, based on the idea that percentages do not denote degree quantifiers, but rather individual degrees in the range of domain-restricted proportional measure functions, as in Solt (2018).
- (72)
- ⟦ n percent ⟧ = n%
If so, percentages can directly saturate the differential argument of -ter- ‘-er’ when we are dealing with domain-restricted proportional measure functions. This entry derives absolute proportional readings, since the differential percentage will correspond directly to the difference between the two measurements; percentages are expected to behave exactly like any non-relative differential measure phrases, which is the right result for absolute proportional readings. But here also lies the limitation of this approach. By eliminating the variable C in the denotation of the percentage, it is now not possible to derive the relative readings of differential percentages. For these readings the quantificational entry in (55) is still required. We cannot at this point exclude such an ambiguity analysis of percentages. However, since our aim is to explore to what extent we can achieve unified accounts of the relevant phenomena, we put this option aside.14
We have argued that differential percentages provide further evidence for a proportional μ-based analysis of proportionality in nominal measurement. We have shown that even in the presence of a relative modifier proportional measure functions are necessary to derive the full range of available readings. Once we also pay attention to differences between two types of proportional measure phrases (domain-restricted and non-restricted functions) we can also correctly predict the distribution of absolute proportional readings. In what follows we proceed to apply a proportional μ-based analysis to Greek juxtaposed and partitive measurement structures.
4 Reverse proportional readings in juxtaposed measurement structures
This section provides an analysis of reverse proportional readings that arise by use of percentages in juxtaposed measurement constructions, as in (73). As in the German example discussed briefly in section 2.2, (73) only gives rise to reverse proportional readings and is thus true in a context in which we hired 10 people half of which were students. We first argue that the phrase peninta tis ekato fitites ‘fifty percent students’ is indeed an instance of a nominal measurement structure. In order to do so we compare it with a case of absolute measurement, as in (74). We then take a closer look at the availability of reverse proportional readings in juxtaposed measurement. We show that the availability of such readings correlates with the availability of absolute proportional readings in the corresponding comparatives. This provides a first motivation to pursue a proportional μ-based analysis. We provide further motivation by showing that the modifier-based analysis of Pasternak & Sauerland (2022), which crucially relies on focus to generate reverse proportionality, under-generates. We proceed with our own analysis which generates reverse proportional readings in juxtaposed measurement in the same way that we generated absolute proportional readings in comparatives. To achieve a unified analysis of relative modifiers, however, we need to rethink our analysis of differential comparatives.
- (73)
- Exthes
- yesterday
- proslavame
- hired.1pl
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- fitites.
- students.pl.acc
- ‘Thirty percent of the people we hired yesterday were students.’
- (74)
- Exthes
- yesterday
- faghame
- ate.1pl
- tria
- three
- kila
- kilo.pl.acc
- mila.
- apple.pl.acc
- ‘We ate three kilos of apples yesterday.’
4.1 Juxtaposed nominal measurement
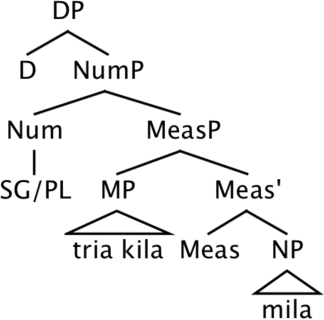
Juxtaposed measurement structures with absolute measures, as in (74), are comprised of a substance noun, a measure noun, and a numeral. The substance noun and the absolute measure noun, which inflect for case and number, bear the same case. Relative measures like tis ekato ‘percent’ do not inflect for case or any phi-features. In fact, tis ekato ‘percent’ has itself the form of a DP as it is built out of the definite determiner in its plural dative form tis and the numeral ekato ‘hundred’. Morphological dative has been replaced in Modern Greek by the genitive, so we are dealing with a fixed expression.15 Case is determined by the position of the nominal construction in the sentence. For example, the substance and measure noun bear nominative when in subject position, as in (75) and (76).16 We conclude that the juxtaposed measurement structure is a Determiner Phrase which is an argument of the verb and case-marked by it, see Alexiadou et al. (2007) for an overview.
- (75)
- Exthes
- yesterday
- katanalothikan
- consumed.pass.3pl
- tria
- three
- kila
- kilo.pl.nom
- mila.
- apple.pl.nom
- ‘Thirty percent of what was consumed yesterday was apples.’
- (76)
- Exthes
- yesterday
- etreksan
- ran.3pl
- ston
- in.the
- marathonio
- marathon
- trianta
- thirty
- tis
- the.dat
- ekato
- hundred.dat
- fitites.
- student.pl.nom
- ‘Thirty percent of the people that ran the marathon yesterday were students.’
Notice that Greek allows a range of word-orders, usually conditioned by information structure. In (75) and (76) above, we used post-verbal subjects. Reverse proportional readings seem to require that the juxtaposed structure appears in post-verbal position. In the presence of multiple arguments, reverse proportional readings require the nominal construction to appear in sentence-final position, as in (77). There is significant controversy in the literature on the distribution and analysis of different word-orders in Greek, see Oikonomou & Alexiadou (2021) for a recent summary. At this point, we cannot offer a more concrete proposal about the interaction of reverse proportionality with the usually subtle information structural effects that condition word-order variation in Greek.
- (77)
- Exthes
- yesterday
- dhosame
- gave.1pl
- afksisi
- raise
- se
- to
- trianta
- thirty
- tis
- the.dat
- ekato
- hundred.dat
- fitites
- student.pl.acc
- ‘Thirty percent of the people we gave a raise to yesterday were students.’
Nominal constructions in adjunct positions also allow reverse proportional readings, as in (78).
- (78)
- Exthes
- yesterday
- taksidhepsame
- travelled.1pl
- me
- with
- trianta
- thirty
- tis
- the.dat
- ekato
- hundred.dat
- fitites.
- student.pl.acc
- ‘Thirty percent of the people we travelled with yesterday were students.’
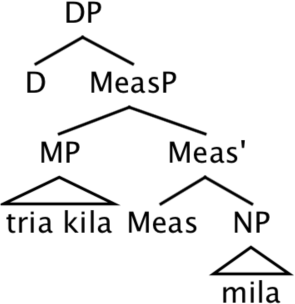
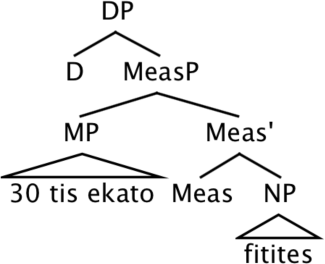
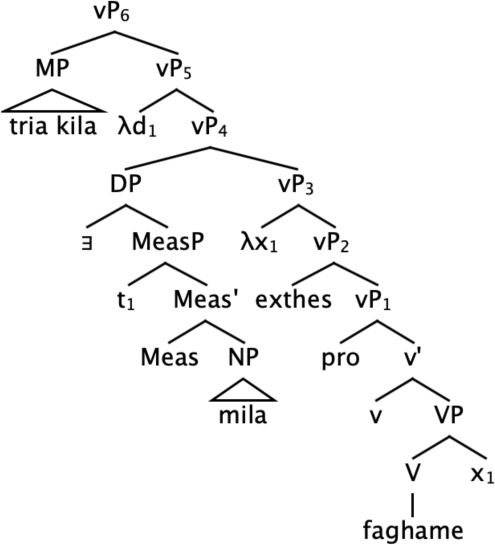
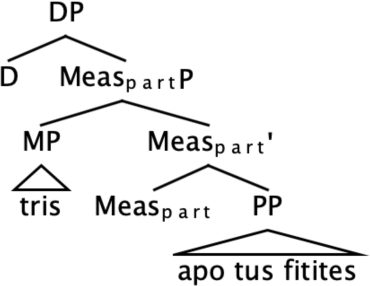
The internal constituency of juxtaposed absolute measurement has been an issue of considerable debate in the literature (Alexiadou et al. 2007 for overview).17 We assume a structure as in (79), where the absolute measure tria kila ‘three kilos’ forms a constituent (labelled MP, Measure Phrase) and is introduced in the specifier of a functional head Meas in the extended projection of the substance NP mila ‘apples’. We extent this analysis to juxtaposed relative measures with percentages in (80). Following Pasternak and Sauerland (2022) we assume that the Determiner Phrase is headed by a covert existential quantifier.18
- (79)
- (80)
The structure we adopt is mono-projectional in the sense that a single nominal is projected (see Stavrou 2003, Alexiadou & Stavrou 2020 for arguments in favor of a mono-projectional analysis of Greek absolute juxtaposed measurement.) We assume that semi-lexical nouns like kilo ‘kilo’ acquire case via agreement with the substance NP. We have assumed here that the numeral and the semi-lexical noun form a constituent. This analysis explains the fact that both the MP and the substance noun can be left-dislocated in Greek. This is so for both absolute and relative measurement, as shown in (81) and (82), respectively.19
- (81)
- a.
- Fitites
- student.pl.acc
- proslavame
- hired.1pl
- exthes
- yesterday
- trianta
- thirty
- tis
- the.dat
- ekato.
- hundred.dat
- ‘Thirty percent of the people we hired yesterday were students.’
- b.
- Trianta
- thirty
- tis
- the.dat
- ekato
- hundred.dat
- proslavame
- hired.1pl
- exthes
- yesterday
- fitites.
- student.pl.acc
- ‘Thirty percent of the people we hired yesterday were students.’
- (82)
- a.
- Mila
- apple.pl.acc
- faghame
- ate.1pl
- exthes
- yesterday
- tria
- three
- kila.
- kilo.pl.acc
- ‘We ate three kilos of apples yesterday.’
- b.
- Tria
- three
- kila
- kilo.pl.acc
- faghame
- ate.1pl
- exthes
- yesterday
- mila.
- apple.pl.acc
- ‘We ate three kilos of apples yesterday.’
One area where the absolute and relative measures differ in their behavior is verbal agreement. In the case of absolute measurement, verbal agreement in number depends on the number of the measurement construction, which itself depends on the number of the semi-lexical number, as shown in (83) and (84). In the case of relative measurement, however, number on the verb is always plural, as shown in (85). We will provide an analysis of these agreement patterns in section 4.4.
- (83)
- Exthes
- yesterday
- katanalothike
- consumed.pass.3sg
- ena
- one
- kilo
- kilo.sg.nom
- mila.
- apple.pl.nom
- ‘One kilo of apples was consumed yesterday.’
- (84)
- Exthes
- yesterday
- katanalothikan
- consumed.pass.3pl
- tria
- three
- kila
- kilo.pl.nom
- mila.
- apple.pl.nom
- ‘Three kilos of apples were consumed yesterday.’
- (85)
- Exthes
- yesterday
- *proslifthike/
- hired.pass.3sg
- proslifthisan
- hired.pass.3pl
- ena/
- one
- trianta
- thirty
- tis
- the.dat
- ekato
- hundred.dat
- fitites.
- student.pl.acc
- ‘One/Thirty percent of the people that were hired yesterday were students.’
Before moving on, we should mention that reverse proportional readings in Greek can also be generated with an adverbial strategy, as in (86), where the percentage appears as part of an adverbial PP, headed by kata ‘by’. An analysis of adverbial reverse proportional readings lies outside the scope of this paper. The existence of this strategy does raise the possibility, however, that the structures we have considered so far also involve adverbial percentages. In this case it would in principle even be possible to assume that the adverbial percentage attaches to the DP projected by the substance noun, explaining the fact that the whole phrase trianta tis ekato fitites ‘thirty percent students’ has the properties and distribution of a DP.
- (86)
- Exthes
- yesterday
- proslavame
- hired.1pl
- kata
- by
- trianta
- thirty
- tis
- the.dat
- ekato
- hundred.dat
- fitites.
- student.pl.acc
- ‘Thirty percent of the people we hired yesterday were students.’
The main reason to reject such an extension of the adverbial strategy has to do with the fact that PP percentages and bare percentages do not have the same distribution. Recall that juxtaposed relative measurement constructions can appear inside PPs, as we saw in (87) and (88) above, giving rise to a reverse proportional reading. PP-percentages, on the other hand, are ungrammatical in these positions.
- (87)
- *Exthes
- yesterday
- dhosame
- gave.1pl
- afksisi
- raise
- se
- to
- kata
- by
- trianta
- thirty
- tis
- the.dat
- ekato
- hundred.dat
- fitites.
- student.pl.acc
- ‘Thirty percent of the people we gave a raise to yesterday were students.’
- (88)
- *Exthes
- yesterday
- taksidhepsame
- travelled.1pl
- me
- with
- kata
- by
- trianta
- thirty
- tis
- the.dat
- ekato
- hundred.dat
- fitites.
- student.pl.acc
- ‘Thirty percent of the people we travelled with yesterday were students.’
Moreover, PP-percentages can appear in more positions within the clause than bare percentages. So, whereas PP-percentages can appear pre-verbally, as in (89), bare percentages cannot, as shown in (90). The same is true of the clause-final position in (91) and (92). We thus reject an adverbial analysis of percentages in juxtaposed measurement structures.
- (89)
- Exthes
- yesterday
- kata
- by
- trianta
- thirty
- tis
- the.dat
- ekato
- hundred.dat
- proslavame
- hired.1pl
- fitites.
- student.pl.acc
- ‘Thirty percent of the people we hired yesterday were students.’
- (90)
- *Exthes
- yesterday
- trianta
- thirty
- tis
- the.dat
- ekato
- hundred.dat
- proslavame
- hired.1pl
- fitites.
- student.pl.acc
- ‘Thirty percent of the people we hired yesterday were students.’
- (91)
- Exthes
- yesterday
- proslavame
- hired.1pl
- fitites
- student.pl.acc
- kata
- by
- trianta
- thirty
- tis
- the.dat
- ekato.
- hundred.dat
- ‘Thirty percent of the people we hired yesterday were students.’
- (92)
- *Exthes
- yesterday
- proslavame
- hired.1pl
- fitites
- student.pl.acc
- trianta
- thirty
- tis
- the.dat
- ekato.
- hundred.dat
- ‘Thirty percent of the people we hired yesterday were students.’
4.2 The distribution of reverse proportionality
Before moving to our analysis, we present further motivation for seeking an alternative to a modifier-based analysis. We first observe a correlation between the availability of juxtaposed measurement structures with percentages and the absolute proportional readings of the corresponding comparatives. We then turn to the issue of focus-sensitivity.
We have seen that whereas readings based on domain-restricted measure functions, as in (93), give rise to absolute proportional readings of differential percentages, readings based on non-restricted measure functions, as in (94), do not.
- (93)
- Context C: We hired 75 students out of 100 hirees yesterday (i.e.75%) and 100 students out of 400 hirees today (i.e. 25%).
- Exthes
- yesterday
- proslavame
- hired.1pl
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- perisoterus
- more.pl.acc
- fitites
- student.pl.acc
- apo
- from
- oti
- rel
- simera.
- today
- ‘We hired fifty percent more students yesterday than we did today.’
- (94)
- Context C: There are 75 road signs per mile in this highway and 25 road signs per mile in that one.
- #Afti
- this
- i
- the
- leoforos
- highway
- exi
- has.3sg
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- perisotera
- more.pl.acc
- simata
- road.sign.pl.acc
- apo
- from
- ekini.
- that
- ‘This highway has 50 percent more road signs than that one.’
We observe that this contrast carries over to the availability of proportional readings with percentages in juxtaposed measurement structures. Whereas, as we have seen, (95) is available, it is not possible for (96) to have a reading based on the density of road signs in the highway.20
- (95)
- Exthes
- yesterday
- proslavame
- hired.1pl
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- fitites.
- student.pl.acc
- ‘Thirty percent of the people we hired yesterday were students.’
- (96)
- #Afti
- this
- i
- the
- leoforos
- highway
- exi
- has.3sg
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- simata.
- road.sign.pl.acc
- ‘This highway has fifty percent road signs.’
This pattern generalizes to all non-restricted proportional measures. To give one more example, consider the proportional reading of the comparative in (97) based on the proportional measures in (98). Such measures cannot support an absolute proportional reading, as shown in (99), and neither is it available in the juxtaposed measurement structure in (100). As in the case of absolute proportional readings in comparatives the intuition is that the percentage will only be felicitous in juxtaposed measurement if it can be taken to directly specify a degree in the dimension of the underlying proportional measure function.
- (97)
- I
- the
- Athina
- Athens
- exi
- has.3sg
- perisotera
- more.pl.acc
- aftokinita
- car.pl.acc
- apo
- from
- ti
- the
- Nea
- New
- Iorki.
- York
- ‘Athens has more cars than New York.’
- (98)
- a.
- μ1 = λx. |x|⁄|people in Athens|
- b.
- μ2 = λx. |x|⁄|people in New York|
- (99)
- Context: There are 75 cars per 100 inhabitants in Athens and 25 cars per 100 inhabitants in New York.
- #I
- the
- Athina
- Athens
- exi
- has.3sg
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- perisotera
- more.pl.acc
- aftokinita
- car.pl.acc
- apo
- from
- ti
- the
- Nea
- New
- Iorki.
- York
- ‘Athens has fifty percent more cars than New York.’
- (100)
- #I
- the
- Athina
- Athens
- exi
- has.3sg
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- aftokinita.
- car.pl.acc
- ‘Athens has fifty percent cars.’
Our claim is not that modifier-based analyses cannot account for the unavailability of (96) and (100). For the reading of, e.g., (100), to be generated in such an account, the denominator of the percentage would have to measure the cardinality of the inhabitants of Athens. But recall that since in the account of Pasternak & Sauerland (2022) the denominator is strictly determined by grammatical means, i.e. the landing site of the QR-ed nominal and the focus structure of its sister constituent, there is simply no way to generate the intended meaning. Since, however, such an analysis has nothing to say about the derivation of absolute proportional readings in comparatives, the observed correlation will have to be coincidental. On the other hand, if, as we will propose in the next section, the proportional readings of juxtaposed measurement structures require the presence of a domain-restricted proportional measure function, just like we have argued for the absolute proportional readings of differential comparatives, the correlation follows naturally.
Consider next the issue of focus-sensitivity, which in the account of Pasternak & Sauerland (2022) is necessary to generate the reverse proportional reading of juxtaposed structures. Indeed, the nominals that head juxtaposed measurement structures do receive the main stress of the sentence. Recall, however, that, as we have seen in (76)–(78), there is a strong preference for the nominals to appear in sentence-final position. In this case, it is not clear whether main stress is the result of default stress assignment or the result of F-marking the nominal. More informative are examples where default stress assignment and F-marking produce different stress patterns, like the German example in (40). The moment we move to such examples, however, the empirical picture becomes much murkier. An example like (101) sounds perfectly grammatical to native speakers, but it is almost impossible to figure out what it actually means.
- (101)
- ??Exthes
- yesterday
- proslavame
- hired.1pl
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- ITALUS
- Italian.pl.acc
- fitites.
- student.pl.acc
- ‘Intended: Fifty percent of the students we hired yesterday were Italian.’
The most natural way to convey the intended meaning is to use a hanging topic, as in (102). Hanging topics in Greek (Anagnostopoulou 1994) are base-generated in their sentence-initial position and receive widest scope. This is confirmed by examples like (103), where the topicalized nominal cannot possibly be linked to any position lower in the structure. Yet (103) has a proportional reading where the percentage specifies the proportional relation of the number of students we hired to the number of waiters we hired.
- (102)
- Oso
- as
- ja
- for
- fitites,
- student.pl.acc
- exthes
- yesterday
- proslavame
- hired.1pl
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- ITALUS.
- Italian.pl.acc
- ‘Thirty percent of the students we hired yesterday were Italian.’
- (103)
- Oso
- as
- ja
- for
- servitorus,
- waiter.pl.acc
- exthes
- yesterday
- proslavame
- hired.1pl
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- FITITES.
- student.pl.acc
- ‘Thirty percent of the waiters we hired yesterday were student.’
One cannot simply claim that the structures in (102) and (103) are necessary because F-marked constituents in Greek have to appear in sentence final position. For one thing, there is no such requirement in the language. For example, mono ‘only’ can associate with the adjectival modifier in (104), even if this does not appear in sentence-final position.
- (104)
- Exthes
- yesterday
- proslavame
- hired.1pl
- mono
- only
- ITALUS
- Italian.pl.acc
- fitites.
- student.pl.acc
- ‘We only hired ITALIAN students yesterday.’
Moreover, the analysis in Pasternak & Sauerland (2022) simply cannot generate the observed proportional readings of (102) and (103) even if we do assume that Italus and fitites are F-marked. Take for example (103). For the observed meaning to be generated the denominator should specify the number of waiters we hired. But there is no possible landing site for the QR-ed phrase that would provide the right argument to the percentage. At best, the account generates a reading, where the percentage specifies the relation of the number of students we hired to the total number of people (rather than waiters) we hired. It might be possible to save the account by alluding to the known fact that focus-alternatives simply restrict rather than fully determine the domain of quantification of focus-sensitive quantifiers. But this is not how focus-sensitivity works in Pasternak & Sauerland (2022), where the focus value of the constituent the percentage composes with only enters the truth-conditional meaning via the effects of the focus presupposition on the domain of the degree predicate. There is no space in the account for context sensitivity in its current form.21 We will argue in the next section that an analysis that allows context sensitivity to enter the derivation of these readings solely via the contextually supplied proportional measure function faces no similar issues.
4.3 Analysis
We can now proceed to present our analysis of proportional readings in juxtaposed measurement structures. As discussed above, the analysis should (a) explain the correlation between these readings and absolute proportional readings in comparatives, (b) allow enough context sensitivity to derive examples like (102) and (103) where the measures involved cannot be derived solely by grammatical means, (c) but not in a way that sneaks in unwanted readings, like the ones based on non-restricted proportional measure functions in (100). The key ingredient of the analysis that helps us derive objectives (a) and (b) are domain-restricted proportional measure functions. In section 4.3.1 we provide an analysis based on domain-restricted measure functions that also assumes the entry for percentages which we argued is necessary to derive all readings of percentages in differential comparatives. As we will see, however, the context sensitivity introduced in the meaning of percentages leads to an over-generation problem. To solve this issue and still achieve a unified treatment of percentages in both juxtaposed structures and differential comparatives, we will need to revise both the meaning of percentages and the meaning of differential comparatives. We make a concrete proposal to this end in section 4.3.2.
4.3.1 Reverse proportionality with domain-restricted proportional measure functions
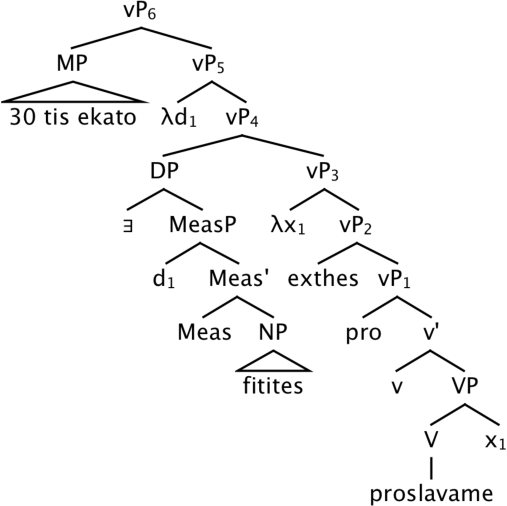
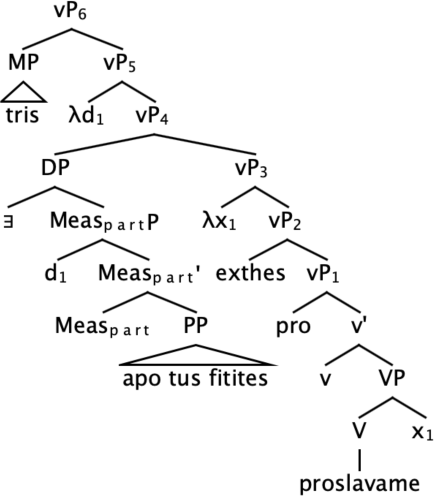
Recall the syntax we assume for juxtaposed measurement structures like (73) in (105). A head Meas introduces measures and mediates the relationship between the bare noun and the percentage. The whole DP, which has the type of a generalized quantifier, since the head D is assumed to be an existential quantifier, undergoes QR to a propositional node, vP, in the partial derivation provided below. In the quantificational analysis of percentages, we have been assuming, the percentage will also QR out of the DP. In order to derive reverse proportional readings, we simply need to assume that the contextually supplied measure function is the domain-restricted proportional measure function in (111). If so, the percentage specifies the relation between the proportion of students we hired yesterday (relative to the total number of hirees) to MAX(C). Given that the underlying function is domain-restricted, MAX(C) will be 1 if the variable C is resolved to the set of degrees in the domain of the degree predicate in vP5. The result is verified in (113) for a context in which we hired 10 people, five of who are students.
- (105)
- (106)
- ⟦ Meas ⟧c = λPet λd λx. P(x) & μc(x) ≥ d
- (107)
- ⟦ ∃ ⟧c = λPet λQet. ∃x [P(x) & Q(x)]
- (108)
- ⟦ DP ⟧c = λQet. ∃x [STUDENT(x) & Q(x) & μc(x) ≥ d1]
- (109)
- ⟦ vP5 ⟧c = λd. ∃(x) [STUDENTS.WE.HIRED.YEST(x) & μc(x) ≥ d]
- (110)
- (111)
- μ = λx :x ⊑ ⊔ WE.HIRED.YEST. |x|⁄|⊔ WE.HIRED.YEST|
- (112)
- (113)
The derivation of reverse proportional readings is exactly parallel to that of absolute proportional readings in comparatives. The only difference is the measurement in the numerator of the percentage. The account predicts, then, that non-restricted measures (and non-proportional measures like cardinality) will not be licensed because their domain does not include a maximal degree.22
Notice that there are two sources of context sensitivity in the proposed analysis; the contextually resolved measure function μc in the meaning of Meas, and the variable C over sets of degrees in the meaning of the percentage. Each of these raise issues of overgeneration. Consider first μc. Although the account can successfully exclude non-restricted proportional measure functions as values of μc, it still might permit one too many domain-restricted functions. Nothing we have said so far prevents μc to be resolved to the function in (114). Based on this function the percentage in examples like (73) could end up specifying the proportional relation of the number of students we hired to the total number of students. This reading is identical to the forward proportional reading of partitive measurement structures. Since, we believe that it is not possible to exclude functions like (144) without at the same time excluding the ones that generate reverse proportional readings, we want to suggest that the source of the marginality of readings based on (114) is the availability of the corresponding partitive measurement structure. One possible reason for partitive measurement to be preferred in this case is that in partitive measurement the sum of students is introduced with a definite DP. The choice of structure, then, could be guided by Maximize Presupposition (Heim 1991), the principle which, everything else being equal, favors expressions with stronger presuppositions. Since the definite phrase ton fititon ‘the students’ in partitive measurement carries uniqueness and familiarity presuppositions, while the bare plural fitites ‘students’ in juxtaposed measurement doesn’t carry any presuppositions, the partitive will be favored. Although we do not provide a full implementation of this idea at this point, we see no reason why it cannot be worked out in detail without affecting the core of our proposal.
- (114)
- μ = λx :x ⊑ ⊔ STUDENTS. |x|⁄|⊔ STUDENTS|
The second source of context sensitivity, however, raises a more serious challenge. Assume that μc is resolved to a non-proportional measure function like cardinality. The resulting reading will then depend on the choice of C. In the case of example (73), this derivation will generate a reverse proportional reading if C is resolved to the set of degrees in (115). The percentage will specify the proportional relation of the number of students we hired to the total number of people we hired. This is of course unproblematic. But, again, the same derivation will generate a forward proportional reading if C is resolved to the degree predicate in (116).
- (115)
- C = {d|μ#(⊔HIREES) ≥ d}
- (116)
- C = {d|μ#(⊔STUDENTS) ≥ d}
More than that, in the case of examples like (73), nothing prevents C to be resolved to the degree predicate in (117) giving rise to a density reading in which the percentage specifies the proportional relation of the number of road signs in the highway to the number of miles that represent the length of the highway.
- (117)
- C = {d|μ#(⊔ MILES.OF.HIGHWAY) ≥ d}
One way to exclude the offending readings would be to assume that Meas restricts the possible values of μc to domain-restricted proportional measure functions. This would in essence be a version of a lexical analysis of proportionality that would treat the proportional readings of juxtaposed measurement structures in a crucially different way than the proportional readings of other measurement structures, like comparatives with and without percentages, since for these cases it wouldn’t be possible to restrict the meaning of the functional head introducing measures in the same way. Since this approach goes against the spirit of unification that we are pursuing in this paper, we will put it aside. The option we will pursue instead is to eliminate the offending source of contextual sensitivity in the meaning of the percentage. In fact, it is not difficult to come up with an entry for percentages that would give us the right result. For example, using the entry assumed by Pastern & Sauerland (2021) repeated in (118) would do just that.
- (118)
The issue that arises, however, is that contextual sensitivity in the meaning of the percentage was crucial in our analysis of the three readings of percentages in differential comparatives. The question, then, is whether we can come up with an entry for percentages that at the same time (a) does not include a variable over degree predicates and (b) generates all readings of differential percentages. We argue in the next section that this is possible, but only once we revise our analysis of differential comparatives.
4.3.2 Percentages without context sensitivity
Let us take the entry in (118) as our starting point and consider why it cannot account for all readings of percentages in differential comparatives under our current assumptions. Recall that in relative cardinal readings the percentage specified the relation of two cardinalities, the one representing the difference between the measurements in the main- and than-clauses and the one representing the measurement in the than-clause. In the relative proportional reading, it specified the relation of two proportions, the one representing the difference between the two proportions and the one representing the measurement in the than-clause. Finally, in the absolute proportional reading the percentage specifies again the relation of two proportions, the one representing the difference between the two proportions and the one representing the maximal value in the underlying dimension of measurement. The problem with the entry in (118), as it stands, is that the entry requires that the degree in the denominator is a maximal degree in the domain of the relevant degree predicate. Yet this only appears to be the case for absolute proportional readings. In the case of relative cardinal and proportional readings, the degree in the denominator is the maximal degree of the degree predicate supplied by the than-clause, not the maximal degree of the degree predicate that appears in the numerator (i.e. the one representing the difference between the two measurements).
To solve this problem in a unified way we need the differential degree predicate to simultaneously be able to provide (a) the difference between the two measurements (since this is what appear in the numerator in all readings), (b) the measurement associated with the than-clause (for both non-proportional and proportional measures, since this appears in the denominator in the case of relative cardinal and proportional readings), and (c) the maximal degree in the range of a domain-restricted proportional measure function (if one is chosen, as has to be the case for absolute proportional readings). The differential degree predicate in our analysis simply does not provide enough information.
In that direction, we propose to revise the meaning of the differential comparative morpheme, as in (119).23
- (119)
- ⟦ -ter- ⟧c = λd: d ≥ MAX(T). λTdt λMdt. d ≥ MAX(M)
Crucially, we will also assume that all differential measure phrases (both absolute and relative ones) denote degree quantifiers and undergo QR. The LF of an example with an absolute measure phrase, like (120), will, thus, be as in (121).
- (120)
- Exthes
- yesterday
- proslavame
- hired.1pl
- tris
- three
- perisoterus
- more.pl.acc
- fitites
- student.pl.acc
- apo
- from
- oti
- rel
- simera.
- today
- ‘We hired three more students yesterday than we did today.’
- (121)
- [ [MP tris] [vP λ1 [[ [t1 -ter-] [ λd [ simera proslavame d-periso- fitites ]] ]
- [ λd [ exthes proslavame d-periso- fitites ]] ]] ]
Since the function of the than-clause in this analysis is to restrict the domain of the differential predicate, the vP denotes the degree predicate in (122). This predicate picks out the degrees that are greater or equal to the number of students we hired today and less or equal than the number of students we hired yesterday. In a context in which we hired 10 students yesterday and 7 students today, (122) picks out the set of degrees of cardinality in (123), or the interval in (124).
- (122)
- ⟦ vP ⟧c = λd: d ≥ MAX(λd.∃x[STUDENTS.HIRED.TOD(x) & μ#(x) ≥ d]).
- d ≤ MAX(λd.∃x[STUDENTS.HIRED.YEST(x) & μ#(x) ≥ d]).
- (123)
- {7, 8, 9, 10}
- (124)
- [7,10]
To get the intended interpretation we now relegate the job of extracting the difference between the two measurements to the differential measure phrase itself. There are different ways to achieve this.24 We assume that an absolute measure has the denotation in (125), where DIM# is the set of degrees measuring cardinality and length takes the measure of an interval, as in (126).25
- (125)
- ⟦ tris ⟧c = λDdt: dom(D) ⊆DIM#. LENGTH(D) = 3
- (126)
- The LENGTH of an interval I, LENGTH(I), with endpoints a, b is b – a if I is bounded and ∞ if I is unbounded.
The presupposition in (125) makes sure that the measure phrase and the predicate of degrees it takes as an argument deal in the same dimension. Since the maximal degree in (122) is the number of students we hired yesterday (i.e. the maximal degree of the predicate provided by the main clause) and the minimal degree is the number of students we hired today (i.e. the maximal degree of the predicate provided by the than-clause), the two degrees specify the endpoints of the relevant interval and the absolute measure phrase correctly ends up specifying the difference between the two degrees, as required.
- (127)
- LENGTH([7,10]) = 3
We can now revise the entry of n percent as in (128). This will ensure that in comparatives the value in the numerator will always represent a difference, as required.
- (128)
A problem persists, however. The entry in (128) will always pick out the maximal degree in the domain of the differential predicate as the value of the denominator. To account for the full range of readings of differential percentages (particularly the relative cardinal and proportional readings), we need to allow ourselves more leeway in the choice of denominator. Taking a hint from Bale’s (2022) entry for partitive of in section 2.1, we revise the entry of n percent, as in (129). ENDPOINTa is a contextually set function from degree predicates to degrees that can be set to either ENDPOINTt, in which case it returns the maximal degree in the domain of the degree predicate, or to ENDPOINTb, in which case it returns the minimal degree in the domain of the degree predicate.
- (129)
With the entry in (129) and the revised entry for the differential comparative morpheme in (119) we have the ingredients to generate all the readings of differential percentages. We repeat our example in (130) and its LF in (131).
- (130)
- Exthes
- yesterday
- proslavame
- hired.1pl
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- perisoterus
- more.pl.acc
- fitites
- students.pl.acc
- apo
- from
- oti
- rel
- simera.
- today
- ‘We hired (thirty percent) more students yesterday than we did today.’
- (131)
- [ [peninta tis ekato] [vP λ1 [[ [t1 -ter-] [ λd [ simera proslavame d-periso- fitites ]] ]
- [ λd [ exthes proslavame d-periso- fitites ]] ]] ]
There are two points of choice in calculating the meaning of (131); the choice of measure function and the choice of ENDPOINT function. The type of measure function will determine whether we are dealing with a cardinal or a proportional reading. The choice of ENDPOINT function will determine whether we are dealing with a relative or an absolute reading. Consider first relative cardinal readings in the context in (132).
- (132)
- Context A: We hired 75 students yesterday and 50 students today.
To generate cardinal readings we assume, of course, that the measure function is resolved to the cardinality function. If so, the differential predicate is as in (133). In the context of (132), this predicate specifies the interval in (134). The length of this interval will be the value of the numerator in the meaning of the percentage.
- (133)
- ⟦ vP ⟧c = λd: d ≥ MAX(λd.∃x[STUDENTS.HIRED.YEST(x) & μ#(x) ≥ d]).
- d ≤ MAX(λd.∃x[STUDENTS.HIRED.TOD(x) & μ#(x) ≥ d])
- (134)
- [50, 75]
Consider next the ENDPOINT function. Since the measure in the differential predicate is cardinality, which has no maximal degree in its range, the domain of the degree predicate in (133) also contains no maximal degree. ENDPOINTt is therefore not an available option. Since, however, the degree predicate is domain-restricted, ENDPOINTb is available. ENDPOINTb picks out the minimal degree in the domain of (133), which is the maximal degree in the degree predicate denoted by the than-clause. We thus end up with the required values in the numerator and denominator to generate a cardinal relative reading. This is verified for the context in (132) in (135).
- (135)
We move next to relative and absolute proportional readings, licensed in the contexts in (136a) and (136b) respectively.
- (136)
- a.
- Context B: We hired 75 students out of 100 hirees yesterday (i.e.75%) and 100 students out of 200 hirees today (i.e. 50%).
- b.
- Context C: We hired 75 students out of 100 hirees yesterday (i.e.75%) and 100 students out of 400 hirees today (i.e. 25%).
We assume that the measure functions in the main- and than-clause are resolved in the domain-restricted proportional measure functions in (137). If so, the differential predicate comes out as in (138). In the context of (136b), this predicate specifies the interval in (139). The length of this interval will again be the value of the numerator in the meaning of the percentage.
- (137)
- a.
- μ1 = λx :x ⊑ ⊔HIREES.YEST.|x|⁄|⊔ HIREES.YEST|
- b.
- μ2 = λx :x ⊑ ⊔ HIREES.TOD.|x|⁄|⊔HIREES.TOD|
- (138)
- ⟦ vP ⟧c = λd: d ≥ MAX(λd.∃x[STUDENTS.HIRED.YEST(x) & μ1(x) ≥ d]).
- d ≤ MAX(λd.∃x[STUDENTS.HIRED.TOD(x) & μ2(x) ≥ d])
- (139)
- [.5, .75]
Consider next the ENDPOINT function. Since the measure in the degree predicate is domain-restricted, the differential predicate has both minimal and maximal degrees in its domain. Both ENDPOINTt and ENDPOINTb are thus available options. ENDPOINTb is responsible for the relative proportional reading; it picks out the minimal degree in the domain of (138), which is the maximal degree in the degree predicate denoted by the than-clause. We thus end up with the required values in the numerator and denominator to generate a relative proportional reading, as verified for the context in (136a) in (140).
- (140)
ENDPOINTt, on the other hand, is responsible for the absolute proportional reading; it picks out the maximal degree in the domain of (138), i.e. 1. We thus end up with the required values in the numerator and denominator to generate an absolute proportional reading, as verified for the context in (136b) in (141).
- (141)
Finally, we return to juxtaposed measurement structures, as in (142), and show that the revised entry for n percent is compatible with the proportional μ-based analysis of the previous section. We refer to the syntactic structure in (105).
- (142)
- Exthes
- yesterday
- proslavame
- hired.1pl
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- fitites.
- student.pl.acc
- ‘Thirty percent of the people we hired yesterday were students.’
In the case of juxtaposed measurement, n percent will compose with the predicate in (143). In a context where we hired 50 students out a total number of 100 hirees, the degree predicate in (143) will pick out the interval in (145), assuming that the measure function is resolved to the familiar domain-restricted proportional measure function in (144). The length of this interval will figure in the numerator of the fraction in the percentage.
- (143)
- ⟦ vP5 ⟧c = λd. ∃x[STUDENTS.WE.HIRED.YEST(x) & μ1(x) ≥ d]
- (144)
- μ1 = λx :x ⊑ ⊔ HIREES.YEST.|x|⁄|⊔HIREES.YEST|
- (145)
- [0, .5]
The denominator will again depend on the choice of ENDPOINT function. Since ENDPOINTb picks out zero, which leads to undefinedness, ENDPOINTt, which picks out 1, is the only available option. The analysis thus derives a reverse proportional reading exactly as we saw in the previous section.
- (146)
More generally, the same reasoning leads us to conclude that only degree predicates with a maximal degree in their domain can be arguments of percentages. If there is no such maximal degree, ENDPOINTt is not an option. At the same time, since all the measure functions we are dealing with are built on ratio scales, the degree predicates will always have zero as the minimal degree in their domain; ENDPOINTb will, thus, also not be an option. This excludes measures like cardinality as a choice for μc, but also all non-restricted proportional measures. At the same time, having eliminated the variable C over degree predicates in the meaning of n percent, there is no way to ‘sneak-in’ any offending readings.
4.4 Absolute juxtaposed measurement constructions
To complete the analysis of juxtaposed measurement, we consider next juxtaposed structures with absolute measures, as in (147). Nothing special needs to be said. The head Meas is the same as in the case of relative MPs. Assuming that the measure function is resolved to a function measuring weight in kilograms, the degree predicate that is the argument of the MP specifies the interval in (152). The MP will specify the value of the length of this interval, as in (153), which is equivalent to saying that the weight of the apples we ate yesterday is 3 kilos.
- (147)
- Exthes
- yesterday
- faghame
- ate.1pl
- tria
- three
- kila
- kilo.pl.acc
- mila.
- apple.pl.acc
- ‘We ate three kilos of apples yesterday.’
- (148)
- (149)
- ⟦ Meas ⟧c = λPet λd λx. P(x) & μc(x) ≥ d
- (150)
- ⟦ tria kila ⟧c = λDdt: dom(D) ⊆DIMkg. LENGTH(D) = 3
- (151)
- ⟦ vP5 ⟧c = λd ∃(x) [APPLES.WE.ATE.YEST(x) & μkg(x) ≥ d]
- (152)
- [0,3]
- (153)
- LENGTH([0,3]) = 3
Before moving to partitive measurement constructions, we show that our analysis can provide an explanation of the observed verbal agreement patterns in number. As we will see, the analysis of these patterns provides some additional evidence in favor of a quantificational analysis of n percent. Recall that this was a major difference between absolute and relative measures in juxtaposed measurement; whereas in the case of absolute measurement, the number on the verb depends on the number of the unit noun, the number of the verb is always plural in the case of relative measurement.
- (154)
- Exthes
- yesterday
- katanalothike
- consumed.pass.3sg
- ena
- one
- kilo
- kilo.sg.nom
- mila.
- apple.pl.nom
- ‘One kilo of apples was consumed yesterday.’
- (155)
- Exthes
- yesterday
- katanalothikan
- consumed.pass.3pl
- tria
- three
- kila
- kilo.pl.nom
- mila.
- apple.pl.nom
- ‘Three kilos of apples were consumed yesterday.’
- (156)
- Exthes
- yesterday
- *proslifthike/
- hired.pass.3sg
- proslifthisan
- hired.pass.3pl
- ena/
- one
- trianta
- thirty
- tis
- the.dat
- ekato
- hundred.dat
- fitites.
- student.pl.nom
- ‘One/Thirty percent of the people that were hired yesterday were students.’
We begin with the assumption that the number of the verb depends on the number of DP via agreement. Moreover, we assume that the number of the measurement construction is determined at the level of a functional projection Num in the extended functional projection of the noun. We assume that Num is located above the unit noun (see Stavrou 2003; Alexiadou & Stavrou 2020 for Greek), as in (157) and (158). For ease of exposition, we treat the absolute MP as denoting an individual degree in a dimension of degrees of weight measured in kilos. Nothing changes when we move to the quantification analysis above.
- (157)
- (158)
To provide a concrete implementation, we adopt Scontras’ (2014) analysis of number, according to which the singularity presupposition of the singular feature SG is relativized to a measurement, as in (159). SG carries a one-ness presupposition, so that “every member of a predicate denotation must measure 1” (Scontras 2014: 22).26 The plural feature PL, on the other hand, is semantically vacuous, as in (160). The analysis thus replicates the familiar asymmetry of SG and PL. In contexts where both SG and PL can in principle be inserted, their distribution is regulated by Maximize Presupposition, which favors the derivation with the strictest presupposition, in this case the one with SG.
- (159)
- ⟦ SG ⟧c = λPet: ∀x ∈P [μ(x) = 1]. P
- (160)
- ⟦ PL ⟧c = λPet. P
The singularity presupposition checks whether the degree of every member in the predicate denoted by MeasP in some dimension of measurement equals one. For this analysis to go through, the measure introduced by SG and the measure introduced by Meas are identified. Consider first the case of absolute measurement. In the case of (154), MeasP denotes the predicate in (161). The presupposition of SG is satisfied, so SG is favored over PL. By subject-verb agreement, the number feature of the verb is singular. In the case of (155), on the other hand, MeasP denotes the predicate in (162). The presupposition of SG is not satisfied, so PL is the only option. By subject-verb agreement, the number feature of the verb is plural.
- (161)
- ⟦ MeasP ⟧c = λx. APPLE(x) & μweight.kg(x) ≥ 1
- (162)
- ⟦ MeasP ⟧c = λx. APPLE(x) & μweight.kg(x) ≥ 3
We move next to relative measurement, where number on the verb is always plural. We will see that both analyses with and without proportional measure functions make the right prediction. However, analyses that treat percentages as individual degrees do not. The crucial case is the one with the relative modifier ena tis ekato ‘one percent’ in (156). Why is singular agreement unavailable in this case? Consider first an analysis without proportional measure functions, where proportionality is solely contributed by the percentage. Since the measure function contributed by Meas in this case measures cardinality, the presupposition of SG requires that the cardinality of the students that were hired is one. All we know about this cardinality, however, is that it equals 1% of some other cardinality, the cardinality of the people that were hired. Similar considerations apply in the case of an analysis with proportional measure functions. In that case the presupposition of SG requires that the proportion of the students that were hired to the total number of hirees equals one (or 100%), which, by assertion, is not the case. In an analysis which treats percentages as individual degrees, on the other hand, the presupposition of SG is indeed satisfied, since, in this case, it requires that the proportion of the students that were hired to the total number of hirees equals 1%, which is the case. Such an analysis, then, makes the wrong prediction that singular agreement should be licensed with the relative modifier ena tis ekato ‘one percent’.
5 Forward proportional readings in partitive measurement structures
This section discusses the forward proportional readings that arise by use of percentages in partitive measurement structures, as in (163). We will first discuss some of the morpho-syntactic properties of partitive measurement. We show that cases like (163) are distinct from the juxtaposed structures we discussed previously and should be discussed on a par with absolute partitive measurement, as in (164). We will see, however, that some important differences between relative and absolute measurement do arise. We, then, present the range of proportional and non-proportional readings that partitives give rise to, discuss the analytical challenges that emerge from this picture, and present our current approach.
- (163)
- Exthes
- yesterday
- proslavame
- hired.1pl
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- ton
- the.gen
- fititon /
- students.gen
- apo
- from
- tus
- the
- fitites.
- students.acc
- ‘We hired fifty percent of the students yesterday’
- (164)
- a.
- Exthes
- yesterday
- proslavame
- hired.1pl
- tris
- three
- apo
- from
- tus
- the
- fitites.
- student.pl.acc
- ‘We hired three of the students yesterday.’
- b.
- Exthes
- yesterday
- faghame
- ate.1pl
- tria
- three
- kila
- kilo.pl.acc
- apo
- from
- ta
- the
- mila.
- apple.pl.acc
- ‘We ate three kilos of the apples yesterday.’
5.1 Absolute and relative partitives
Partitives differ from juxtaposed measurement in some obvious ways. First of all, we are clearly dealing with two DP projections, since the inner nominal is definite and projects its own D layer. Moreover, the two nominals, the inner nominal and the measure noun, as seen in the absolute partitive in (164), do not share case. Whereas the case of the measure noun is determined by the syntactic position of the partitive, the inner nominal receives accusative case by the preposition apo ‘from’. An overt PP can also appear in the case of relative measurement. Most frequently, however, the inner nominal appears in genitive case. Notice that genitive did have a partitive function in the diachrony of Greek and can still be found with absolute measurement in some more archaic and formal registers.
Unlike relative juxtaposed measurement, where a definite determiner can only appear under certain conditions and only in the case of absolute measurement, a definite determiner can readily head the partitive, as in (165) and (166), without any apparent difference in meaning. But whereas the number on the definite determiner is always SG with relative measures, in the case of absolute measures, its number value depends on the number of the measure noun.
- (165)
- Exthes
- yesterday
- proslavame
- hired.1pl
- to
- the.sg.acc
- ena/trianta
- one thirty
- tis
- the.dat
- ekato
- hundred.dat
- ton
- the.gen
- fititon /
- students.gen
- apo
- from
- tus
- the
- fitites.
- student.pl.acc
- ‘We hired one/thirty percent of the students yesterday.’
- (166)
- a.
- Exthes
- yesterday
- faghame
- ate.1pl
- to
- the.sg.acc
- ena
- three
- kilo
- kilo.sg.acc
- apo
- from
- ta
- the
- mila.
- apples.pl.acc
- ‘We ate one kilo of the apples yesterday.’
- b.
- Exthes
- yesterday
- faghame
- ate.1pl
- ta
- the.pl.acc
- tria
- three
- kila
- kilo.pl.acc
- apo
- from
- ta
- the
- mila.
- apple.pl.acc
- ‘We ate three kilos of the apples yesterday.’
As in juxtaposed measurement, an overt indefinite determiner is only possible with relative measures and functions as an approximator.
- (167)
- Exthes
- yesterday
- proslavame
- hired.1pl
- ena
- one
- trianta
- thirty
- tis
- the.dat
- ekato
- hundred.dat
- ton
- the.gen
- fititon /
- students.gen
- apo
- from
- tus
- the
- fitites.
- students.pl.acc
- ‘We hired approximately thirty percent of the students yesterday.’
- (168)
- *Exthes
- yesterday
- faghame
- ate.1pl
- ena
- one
- tria
- three
- kila
- kilo.pl.acc
- apo
- from
- ta
- the
- mila.
- apple.pl.acc
- ‘Intended: We ate approximately three kilos of the apples yesterday.’
Partitives also differ from juxtaposed measurement with regard to verbal agreement patterns. Recall that in juxtaposed measurement, relative measures only licensed plural number on the verb, whereas absolute measures licensed both singular and plural, depending on the number of the measure noun. Partitives show the same pattern in the case of absolute measurement, as shown in (169) and (170). In the case of relative measurement, on the other hand, the pattern is reversed. Relative measures only license singular number, as shown in (171). Notice, however, that in positions where the partitive controls agreement on the verb the presence of an overt definite determiner (which, as we saw above, is always SG with relative measures) is strongly preferred.
- (169)
- Exthes
- yesterday
- katanalothike
- consumed.pass.3sg
- ena
- one
- kilo
- kilo.sg.nom
- apo
- from
- ta
- the
- mila.
- apple.pl.nom
- ‘A kilo of the apples was consumed yesterday.’
- (170)
- Exthes
- yesterday
- katanalothikan
- consumed.pass.3pl
- tria
- three
- kila
- kilo.pl.nom
- apo
- from
- ta
- the
- mila.
- apple.pl.acc
- ‘Three kilos of apples were consumed yesterday.’
- (171)
- Exthes
- yesterday
- proslifthike/
- hired.pass.3sg
- *proslifthisan
- hired.pass.3pl
- ??(to)
- the.sg.acc
- ena/trianta
- one thirty
- tis
- the.dat
- ekato
- hundred.dat
- ton
- the.gen
- fititon.
- students.gen
- ‘One/Thirty percent of the people that were hired yesterday were students.’
Notice finally that partitives behave like juxtaposed structures in terms of left-dislocation. The PP/genitive DP can be left-dislocated, as shown in (172a) and (173a). Moreover, the numeral and the semi-lexical/measure noun form a constituent that can be left-dislocated, as shown in (173b) and (173b) for relative and absolute measures, respectively.27
- (172)
- a.
- Apo
- from
- tus
- the
- fitites
- student.pl.acc
- proslavame
- hired.1pl
- exthes
- yesterday
- trianta
- thirty
- tis
- the.dat
- ekato.
- hundred.dat
- ‘We hired thirty percent of the students yesterday.’
- b.
- ?Trianta
- thirty
- tis
- the.dat
- ekato
- hundred.dat
- proslavame
- hired.1pl
- exthes
- yesterday
- apo
- from
- tus
- the
- fitites.
- student.pl.acc
- ‘We hired thirty percent of the students yesterday.’
- (173)
- a.
- Apo
- from
- ta
- the
- mila
- apple.pl.acc
- faghame
- ate.1pl
- exthes
- yesterday
- tria
- three
- kila.
- kilo.pl.acc
- ‘We ate three kilos of the apples yesterday.’
- b.
- ?Tria
- three
- kila
- kilo.pl.acc
- faghame
- ate.1pl
- exthes
- yesterday
- apo
- from
- ta
- the
- mila.
- apple.pl.acc
- ‘We ate three kilos of the apples yesterday.’
It goes beyond the scope of this paper to provide an analysis of partitives that captures all the properties we have observed. In the case of relative partitive structures, a particular challenge that arises is the analysis of structures with overt definite articles.28 Since our current focus is on a different issue, i.e. the locus of proportionality and the interaction of proportionality with partitivity, we put such cases to the side. To be able the to highlight the relevant differences with juxtaposed measurement structures in what follows, we will focus on cases without overt determiners and assume a structure that is minimally different from that assumed for juxtaposed measurement, as in (174) and (175).
- (174)
- (175)
As in juxtaposed structures, the covert head D is taken to be an existential quantifier. We assume that semantic partitivity is located in the meaning of the Measpart head and that the presence of the preposition apo ‘from’ or genitive case is a morpho-syntactic effect with no semantic import. We also assume a mereological account of plurality and adopt a treatment of the definite determiner in terms of the summation operator σ (Link 1983), so that the DPGen/PP phrase containing NP will always have the meaning in (176).29
- (176)
- ⟦ DPGen ⟧c = σx [⟦ NP ⟧c (x)]
Given the quantificational meaning of D and the quantificational analysis of MPs we have adopted, there are two instances of QR, as shown in (177) and (178).
- (177)
- (178)
5.2 Proportional and non-proportional readings of partitive measurement
Following Solt (2018), Bale (2022), and Pasternak & Sauerland (2022) we will introduce partitivity in the meaning of Measpart by restricting the measure functions introduced by Measpart to domain-restricted functions. The question we want to consider is whether we can stick to a non-lexical analysis, where Measpart does not introduce proportionality, as in (179), or we need to move to the entry in (180), as proposed in Bale (2022).
- (179)
- (180)
Let us start by considering the entry in (179). What readings does this entry license? Obviously, resolving μc to a simple non-proportional measure, like cardinality or weight, the entry will derive the readings of examples with absolute MPs like tris ‘three’ and tria kila ‘three kilos’ in (173). In this case the degree predicate that will be the argument of the measure phrase will be the one in (181) for, e.g., cardinality, where s is the sum of students. Assuming we hired three out of 6 students, (181) specifies the interval in (182). The absolute measure phrase tris ‘three’ correctly specifies the length of this interval.
- (181)
- ⟦ vP5 ⟧c = λd. ∃y [y ⊑ σx [STUDENT(x)] & WE.HIRED.YEST(y) & μ#;s(y) ≥ d]
- (182)
- LENGTH([0,3]) = 3
The same resolution of μc can also generate forward/partitive proportional readings, when (181) is the argument of a percentage. Since the function is domain-restricted, the maximal degree in the domain of (181) is the cardinality of the sum of students. Setting the denominator to ENDPOINTt (the only option, since ENDPOINTb picks out zero), the percentage specifies the proportional relation of the cardinality of the students we hired to the cardinality of the sum of students.
- (183)
The entry in (179) also makes successful predictions in case μc is resolved to proportional measure functions. Recall that we wish to derive the fact that an example like (163) only allows for forward/partitive proportional readings, not any other proportional readings. Consider first the proportional measure function in (185). Due to partitivity, the function is actually domain-restricted, as in (186). In a context where we hired 3 out of 6 students, the degree predicate in (184) will pick out the interval [0, .5]. The maximal degree in the domain of the predicate is the maximal degree in the range of μ1;s, , which equals 1. The percentage, thus, specifies correctly the proportional relation of the number of the students we hired to the total number of students.
- (184)
- ⟦ vP5 ⟧c = λd. ∃y [y ⊑ σx [STUDENT(x)] & WE.HIRED.YEST(y) & μ2;s(y) ≥ d]
- (185)
- μ2 = λx. |x|⁄|⊔ STUDENTS|
- (186)
- μ2;s = λx: x ⊑ ⊔STUDENTS. |x|⁄|⊔ STUDENTS|
- (187)
Assume next that μc is resolved to the function in (189), the one that has been responsible for generating reverse proportional readings. Due to partitivity, the function is domain-restricted, as in (190). Crucially, since the domain-restriction is determined grammatically by Measpart, the domain of the function is restricted to sub-aggregates of the sum of students (not the sum of hirees, as before). In a context where we hired 6 people, 3 of whom are students, the degree predicate in (188) will pick out the interval [0, .5]. The maximal degree in the domain of the predicate is the maximal degree in the range of . What is its value? (191) will only be true in contexts in which the cardinality of the sum of students is equal to the cardinality of the sum of people we hired. Then the value will be 1 and the percentage will provide the right proportional specification of the relation of the two proportions. In this context, however, the forward proportional reading also comes out true since . More generally, given the grammatically determined domain-restriction on the measure function and the fact that the only available choice for the denominator in the percentage is ENDPOINTt, any context in which (163) is true under the measure function in (190) will also be a context in which (163) is true under the measure function in (186). The same is true regardless of the choice of proportional measure function, they are all rendered invisible and identical to a measure in which the denominator is identical to the measure of the plural individual denoted by the nominal complement of Measpart.
- (188)
- ⟦ vP5 ⟧c = λd. ∃y [y ⊑ σx [STUDENT(x)] & WE.HIRED.YEST(y) & μ1;s(y) ≥ d]
- (189)
- μ1 = λx. |x|⁄|⊔ HIREES.YEST|
- (190)
- μ1 = λx :x ⊑ ⊔STUDENTS. |x|⁄|⊔ HIREES.YEST|
- (191)
The account achieves, in the presence of percentages, the same result that Bale’s (2022) entry in (180) achieves for partitives in all measurement constructions (and in much the same way). The advantage of Bale’s entry, as we discussed in section 2.1., is that it correctly predicts that partitive measurement prohibits non-partitive proportional readings across the board. For example, we saw that (the English version of) (192) only gives to partitive/forward proportional readings.
- (192)
- Exthes
- yesterday
- proslavame
- hired.1pl
- perisoterus
- more.pl.acc
- apo
- from
- tus
- the
- fitites
- student.pl.acc
- apo
- from
- oti
- rel
- simera.
- today
- ‘We hired more of the students yesterday than today.’
As we will see, however, there is an issue with simply adopting Bale’s entry instead of the one in (179). The issue does not have to do with the distribution of proportional readings, but with how the entry derives non-proportional readings of partitives.
- (193)
Let us first reassure ourselves that we can unproblematically combine Bale’s entry in (193) with the proposed semantics of n percent. Consider, again, the example in (163). Under Bale’s analysis, the degree predicate in (194) is the same regardless of the choice of measure function since the denominators in the specification of all proportional measure functions are factored out. Assuming that the LIMIT function is set to LIMITt, this predicate is exactly identical to the one in (184), except that the proportional measure is grammatically derived. Feeding (194) to a percentage, then, will lead to exactly the same result, a partitive/forward proportional reading.
- (194)
- (195)
Bale claims that the same entry can derive simple cardinal readings when LIMIT is set to LIMITb. He assumes that the minimal degree in the range of a domain-restricted measure function μDIM;x is 1, the measure of the atoms that are a part of x. If so, the meaning of vP5 comes out as in (196); it picks out non-proportional degrees of cardinality.
- (196)
The same setting of LIMIT is said to derive cardinal readings of comparatives like (192). Following Solt (2018), Bale argues that the English version of (192) also has a simple cardinal reading; it can be true in a scenario in which we hired 10 out 20 students yesterday and 8 out of 10 students today. Notice that the proportional partitive reading is false in this scenario.
The first thing to note is that it is not possible to derive cardinal readings in this way under our own assumptions. Since we have been assuming that all the relevant measure functions (domain-restricted ones included) define ratio scales, all the functions discussed here will have a zero degree in their range (even if no individual in the domain of the function is mapped on zero.)30 Setting LIMIT to LIMITb, then, will never be an option in the relevant cases above since this will lead to undefinedness. There is at least one reason to think that this is not an unwelcome result. Contra the judgements reported in Bale (2022), and Solt (2018) for English, we do not detect a simple cardinal reading for the comparative in (192). Indeed, we judge (192) false in the scenario above.31 The problem is, however, that we still need to be able to derive non-proportional readings to handle partitive measurement with absolute measure phrases like tris ‘three’ and tria kila ‘three kilos’. Under current assumptions, only the entry in (179) can derive non-proportional readings.
To summarize, the entry in (179) generates non-proportional readings, but it over-generates proportional readings in comparatives. Adopting Bale’s entry in (180), on the other hand, derives the right proportional readings across the board, but under-generates non-proportional readings. At this point we have not been able to solve this puzzle by defining a single entry for Measpart that at the same time (a) only generates the right proportional readings and (b) only generates non-proportional readings in the presence of absolute MPs. Although this issue does not affect the core empirical domain of interest in this paper (i.e. the interpretation of partitive measurement with relative measures), it affects every analysis of partitive measurement the moment proportional measure functions are admitted (as we have argued is necessary in the previous sections). For the time being, we will assume an ambiguity account, according to which both options are available. Bale’s entry is the default entry for Measpart and the entry in (179) only becomes available as a last resort in the presence of absolute measure phrases. A more principled account awaits to be formulated.
6 Conclusions
This paper addressed a key issue in the grammar of nominal measurement, namely the source of proportionality in relative readings of nominal measurement structures. We identified four available analytical options employed in previous literature. A lexical analysis places proportionality in the meaning of a functional element that introduces measures. A standard-based analysis introduces proportionality via manipulating a contextual standard. A proportional μ-based analysis introduces proportionality via contextually introduced proportional measure functions. Finally, in a modifier-based analysis, proportionality enters the truth-conditions solely via the meaning of a relative modifier. The question is whether nominal measurement structures are (or can be) in some sense inherently proportional (in which case they would be subject to a lexical analysis of some sort or other) or whether proportionality comes into the meaning of proportional measurement via some external factor, like the manipulation of a contextual standard, the choice of a proportional measure function, or the presence of a relative modifier.
We investigated this question focusing in three non-standard-sensitive constructions with relative modifiers in Greek, namely comparatives with differential percentages, reverse proportional readings of juxtaposed nominal measurement structures, and forward proportional readings of percentages of partitives. We argued that the different readings of comparatives with differential percentages provide novel evidence in favor of proportional μ-based analyses. Interestingly, this is so even in the presence of an additional source of proportionality, the meaning of the percentage itself. We additionally provided several reasons to revise modifier-based analyses of proportionality in juxtaposed and partitive measurement structures, at least for the language under investigation, Greek. In the case of juxtaposed measurement, we argued that a proportional μ-based analysis is both sufficient and necessary to derive the distribution of proportional readings we observed. In doing so, it was essential to make use of a difference between two types of proportional measure functions, domain-restricted and non-restricted measure functions. Moreover, in our quest to provide an analysis of percentages that can simultaneously (a) handle their uses in all structures under investigation and (b) solve an over-generation problem faced by our proportional μ-based analysis, we proposed an alternative analysis of differential comparatives and (differential) measure phrases, in which measure phrases do not denote individual degrees but rather measure the lengths of degree predicates. Partitive measurement structures proved to be the most inconclusive case regarding the locus of proportionality and the only one of the cases under investigation for which inherent/lexical proportionality might be required.
Notes
- As shown in Bale & Schwarz (2020), proportional measure functions satisfy known constraints on contextually resolved measure functions, like the Monotonicity constraint (Schwarzschild 2006). [^]
- Like all the measure functions discussed in this paper, proportional measure functions are what in Measurement Theory are called ratio functions (or scales). As such, they have a non-arbitrary zero value in their range (even if no individual in their domain is mapped to zero) and operations like multiplication, division, addition, and subtraction are all meaningful. See Sassoon (2010), Lassiter (2017) for detailed discussion. To confirm that statements about the ratios of proportions are felicitous consider, for example, the examples in (i) under their proportional interpretations.
- (i)
- a.
- Twice as many cooks applied this year as last year.
[^]- b.
- Two times more cooks applied this year than last year.
- Here and throughout, we use small capitals to abbreviate predicates of individuals. [^]
- Similar examples can be constructed with fewer. For reasons of space, we only discuss more in what follows. [^]
- LIMITt is the only available option in these cases, since LIMITb would return zero and lead to undefinedness. We deviate from Bale (2022) on this point. See section 5.2. for discussion. [^]
- This captures the familiar constraint from the adjectival domain (see Kennedy & McNally 2005 and references therein) that percentages and other relative modifiers are only felicitous with closed scale adjectives, as shown in (i).
- (i)
- a.
- The glass is 75% full.
[^]- b.
- #John is 75% tall.
- Pasternak & Sauerland (2022) does not discuss MEAS in relation to Solt’s domain-restricted measure functions. They achieve the same result in a slightly different way, but the desired effect is essentially the same. [^]
- Our treatment of comparatives is based on that in Bale and Schwarz (2020) extended straightforwardly to cover differentials. Many of the details of this analysis are not crucial for our main argument. Our choice is directed by facilitating comparison with the most relevant literature. [^]
- Next to the synthetic form of the comparative, an analytic form, as in (i), also exists. Like the synthetic form, the analytic form is also three-way ambiguous, and will not be discussed further here. See Makri (2018, 2020) and Alexiadou et al. (2021) for discussion of the similarities and differences between the two forms.
[^]
- (i)
- Exthes
- yesterday
- proslavame
- hired.1pl
- peninta
- fifty
- tis
- the.dat
- ekato
- hundred.dat
- pio
- COMP
- polus
- many.pl.acc
- fitites
- students.pl.acc
- apo
- from
- oti
- rel
- simera.
- today
- ‘We hired fifty percent more students yesterday than we did today.’
- Dan Lassiter (p.c.) points out that closed scale adjectives, as in (ii), also show the same type of ambiguity. Example (i) is true if the red glass is 75% full and the blue glass 50% full, but also if the red glass is 75% full and the blue glass 25% full. For another case of an absolute proportional reading see also (ii) from Klecha (2014), which is true if the odds increased from 50% to 60%.
- (i)
- The red glass is 50% fuller than the blue glass.
[^]- (ii)
- The odds increased 10%.
- Just like the measure phrase 2 cm is a degree of height in Mary is 2 cm taller than John. [^]
- Domain-restricted proportional measure functions map their domain to the unit interval [0, 1]. [^]
- This is exactly what motivates Bale & Schwarz (2020) and Bale (2021) to adopt the broader definition of proportional measures in (11), in response to Solt (2018) who supposes that all proportional measures are domain-restricted measures. [^]
- See also the discussion in section 4.4. [^]
- In more colloquial speech the dative tis is often replaced with the plural accusative form of the neuter definite determiner ta, as in ta ekato ‘percent’. [^]
- We restrict our attention to absolute measure phrases with pure measure nouns, like kilo ‘kilo’. The structures discussed here are clearly related to similar cases with container nouns, as in (i), which have usually been discussed in the literature under the rubric of pseudo-partitivity. These cases are famously ambiguous between quantity and container readings. We submit that in their quantity readings container nouns can be treated exactly like the pure measure nouns discussed here and throughout the paper, as also manifested by the fact that they can function as differential measure phrases, as in (ii). In these cases, the measure phrases have regular degree readings, where the degrees represent measures in some non-established unit. We leave aside the important question of the differences between container and quantity readings, since, as far as we can see, it has no bearing on our main point, but see Alexiadou et al. 2007, Alexiadou (2014) and Borer (2005) and references therein for arguments that container and quantity readings should receive distinct syntactic representations.
- (i)
- Ipia/
- drank.1sg
- Espasa
- broke.1sg
- dhio
- two
- potiria
- glass.pl.acc
- krasi
- wine.sg.acc
- ‘I drank/broke two glasses wine.’
[^]- (ii)
- Ipia
- drank.1pl
- dhio
- two
- potiria
- glass.pl.acc
- perisotero
- more.sg.acc
- krasi
- wine.sg.acc
- apo
- from
- esena
- you
- ‘I drank two glasses more wine than you did.’
- A lot of the discussion centers around the proper treatment of the ‘semi-lexicality/-functionality’ of the measure and container nouns that appear in juxtaposed structures, i.e. the fact that they do not appear to project as full-fledged nominals. In the structure we propose, the measure nouns are part of the measure phrase and not part of the functional spine of the DP. Alternatively, semi-lexical nouns like unit nouns (or even tis ekato ‘percent’) can be taken to be heads (perhaps identified with the Meas head in (79) and (80)) in the functional projection of the substance noun. Although such analyses are possible and in principle compatible with all analyses of proportionality considered in this paper, they would need to do more work to explain both the facts in (81) and (82) and the use of phrases like tria kila ‘three kilos’ and trianta tis ekato ‘thirty percent’ as differential measure phrases in comparatives. Things might be different in the case of the container readings mentioned in footnote 16. See Stavrou (2003), Alexiadou et al. (2007) and Klockmann (2017) for extensive discussion on semi-lexicality. [^]
- An overt indefinite determiner, which is homophonous with the numeral one, is available for relative measures, but, in this case, it acts as an approximator, as in (i). The indefinite determiner kapjos ‘some’, on the other hand, which cannot give rise to approximation, is ruled out. We currently have no account of the approximative use of ena ‘one/some’ and its distribution.
[^]
- (i)
- Exthes
- yesterday
- proslavame
- hired.1pl
- ena /
- one
- *kapjo
- some
- trianta
- thirty
- tis
- the.dat
- ekato
- hundred.dat
- fitites.
- student.pl.acc
- ‘Approximately thirty percent of the people we hired yesterday were students.’
- Notice that the examples with fronted MPs in (81b) and (81b) are somewhat more degraded if judged out of context. We believe this is because the fronted position is a topicalized position and MPs are harder to conceive as discourse topics. Both examples are perfectly felicitous if they are answers to questions like ‘What did you hire thirty percent of yesterday?’ and ‘What did you eat three kilos of yesterday?’. [^]
- The only (marginally) available reading of (96) is one in which the percentage specifies the proportional relation of the number of road signs to the total number of items that the highway has/is related to. This of course would be a reading based on a domain-restricted proportional measure. [^]
- To revise the account in a way that allows context sensitivity to determine the value of the denominator, one would minimally need to introduce a variable C over sets of degree predicates in the meaning of the percentage and assume a theory of focus as in Rooth (1992). It is unclear to us at this point whether such an approach can successfully be implemented in this case. Ahn and Sauerland (2015, 2017) pursue this strategy, albeit in an analysis of percentages in which they measure individual rather than quantify over degrees. Pasternak & Sauerland (2022) identify several compositionality problems in the execution of this strategy in Ahn & Sauerland (2015; 2017). As far as we can see these problems would carry over in a degree-based account. Notice, moreover, that any such account would have to explain why focus sensitivity is necessary in the case of juxtaposed structures but not in other measurement structures with percentages, like, e.g., differential percentages in comparatives. [^]
- The observed readings of examples (102) and (103), on the other hand, are predicted to be available if the measure function is resolved to the ones in (i) and (ii), respectively.
- (i)
- μ = λx∶x ⊑ ⊔ STUDENTS.WE.HIRED.YEST. |x| ⁄ |⊔ STUDENTS.WE.HIRED.YEST|
[^]- (ii)
- μ=λx∶x ⊑ ⊔ WAITERS.WE.HIRED.YEST.|x| ⁄ |⊔ WAITERS.WE.HIRED.YEST|
- This proposal has much in common with the analysis of comparatives in vector-based (Faller 2000) and segment-based (Schwarzschild 2012) analyses of comparatives, or the analysis in terms of difference functions in Kennedy & McNally (2005). We have favored an implementation that requires no modification to our underlying assumptions about the ontology of degrees and the syntax-semantics of comparison. Other implementations might be possible. [^]
- Alternatively, we can use a function, which returns the difference between two degrees, as in (i) (cf. Kennedy & McNally 2005).
[^]
- (i)
- The denotation in (125) is a version of the quantificational approach to absolute MPs in von Stechow (2005), in which the numeral picks out the maximal degree of the degree predicate, rather than specify its length. [^]
- Other analyses of nominal number might also be suitable. A comparison between different analyses of nominal number lies beyond the scope of this paper. [^]
- Examples (172b) and (173b) are somewhat degraded out-of-the-blue since MPs are not the best candidates for discourse topics. [^]
- Falco & Zamparelli (2019), discussing similar patterns in Italian, suggest that the definite article in this structure is akin to the definite article that appears in generic predication in these languages, as in (i) for Greek.
[^]
- (i)
- I
- the.pl.nom
- elefantes
- elephants.pl.nom
- exun
- have.3pl
- provoskides.
- trunks
- ‘Elephants have trunks.’
- Alternatively, apo ‘from’ can be identified with Measpart. Nothing really hinges on this choice in what follows. [^]
- As Bale (2022) notes, his account of non-proportional readings also requires that the domains of mass nouns have atomic elements. This is needed in order to account for the non-proportional readings of examples with mass nouns as in (i).
[^]
- (i)
- I removed more of the red paint that was on my left boot than the blue paint that was on my right boot.
- One possible explanation for the discrepancy is that some speakers might take the definite descriptions the students in the main- and than-clause of the comparative to refer to the same sum of students, the sum of all relevant students. A partitive proportional reading then is true in a scenario in which we hired 10 out 20 students yesterday and 8 out of 10 students today, since the proportions that are actually compared are 10/30 and 8/30. [^]
Abbreviations
pl = plural, sg = singular, nom = nominative, gen = genitive, acc = accusative, dat = dative, 1 = first person, 3 = third person, pass = passive, f = focus, comp = comparative, rel = relative pronoun
Funding information
This work has been funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation), Grant AL554/12-1 (#387623969).
Acknowledgements
We are thankful to Stephanie Solt, Dan Lassiter, Rob Pasternak, and Uli Sauerland for helpful discussions, and to Stavroula Alexandropoulou, Nikos Angelopoulos, Maria Barouni, Margarita Makri, and Dimitris Michelioudakis for their judgements. We also wish to thank two anonymous reviewers for their valuable feedback.
Competing interests
The authors have no competing interests to declare.
References
Abusch, Dorit. 2010. Presupposition triggering from alternatives. Journal of Semantics 27(1). 37–80. DOI: http://doi.org/10.1093/jos/ffp009
Ahn, Dorothy & Sauerland, Uli. 2015. The grammar of relative measurement. In D’Antonio, Sarah & Moroney, Mary & Little, Carol Rose (eds.), Semantics and Linguistic Theory (SALT) 25. 125–142. Ithaca, NY: CLC Publications, Cornell University. DOI: http://doi.org/10.3765/salt.v25i0.3062
Ahn, Dorothy & Sauerland, Uli. 2017. Measure constructions with relative measures: Towards a syntax of non-conservative construals. The Linguistic Review 34(2). 215–248. DOI: http://doi.org/10.1515/tlr-2017-0001
Alexiadou, Artemis. 2014. Multiple Determiners and the Structure of DPs. Amsterdam: John Benjamins. DOI: http://doi.org/10.1075/la.211
Alexiadou, Artemis & Haegeman, Liliane & Stavrou, Melita. 2007. Noun Phrase in the Generative Perspective. Berlin, Germany: Mouton de Gruyter. DOI: http://doi.org/10.1515/9783110207491
Alexiadou, Artemis, & Oikonomou, Despoina & Karkaletsou, Fenia. 2021. Double comparatives: structural complexity and evaluativity. Talk presented at the 12th International Conference of Nordic and General Linguistics, Oslo, June 16, 2021.
Alexiadou, Artemis & Stavrou, Melita. 2020. Partitives, pseudopartitives, and the preposition apo in Greek. Linguistics 58(3). 713–743. DOI: http://doi.org/10.1515/ling-2020-0082
Anagnostopoulou, Elena 1994. Clitic Dependencies in Modern Greek. Salzburg: University of Salzburg dissertation.
Bale, Alan. 2022. Partitives, Comparatives and Proportional Measurement. In Gotzner, Nicole & Sauerland, Uli (eds.), Measurements, Numerals and Scales, 11–34. Palgrave Studies in Pragmatics, Language and Cognition. Palgrave Macmillan, Cham. DOI: http://doi.org/10.1007/978-3-030-73323-0_2
Bale, Alan & Schwarz, Bernhard. 2020. Proportional readings of many and few: the case for an underspecified measure function. Linguistics and Philosophy 43. 673–699. DOI: http://doi.org/10.1007/s10988-019-09284-5
Borer, Hagit. 2005. In Name Only. Oxford: Oxford University Press.
Cresswell, Maxwell J. 1976. The semantics of degree. In Partee, Barbara H. (ed.), Montague grammar, 261–292. New York: Academic Press. DOI: http://doi.org/10.1016/B978-0-12-545850-4.50015-7
Falco, Michelangelo & Zamparelli, Roberto. 2019. Partitives and Partitivity. Glossa: a journal of general linguistics 4(1): 111. 1–49. DOI: http://doi.org/10.5334/gjgl.642
Faller, Martina. 2000. Dimensional adjectives and measure phrases in vector space semantics. In Faller, Martina & Kaufmann, Stefan & Pauly, Marc (eds.), Formalizing the Dynamics of Information, 151–170. CSLI Publications, Stanford.
Heim, Irene. 1991. Artikel und Definitheit. In von Stechow, Arnim & Wunderlich, Dieter (eds.), Semantik: Ein internationales Handbuch der zeitgenössischen Forschung, 487–535. Berlin: de Gruyter. DOI: http://doi.org/10.1515/9783110126969.7.487
Heim, Irene & Kratzer, Angelika. 1998. Semantics in Generative Grammar. Wiley-Blackwell.
Herburger, Elena. 1997. Focus and weak noun phrases. Natural Language Semantics 5(1). 53. DOI: http://doi.org/10.1023/A:1008222204053
Keenan, Edward L. & Stavi, Jonathan. 1986. A semantic characterization of natural language determiners. Linguistics and Philosophy 9(3). 253–326. DOI: http://doi.org/10.1007/BF00630273
Kennedy, Chris & McNally, Louise. 2005. Scale structure and the semantic typology of gradable predicates. Language 81(2). 345–381. DOI: http://doi.org/10.1353/lan.2005.0071
Klecha, Peter. 2014. Bridging the divide: Scalarity and modality. Chicago: University of Chicago dissertation.
Klockmann, Heidi. 2017. The design of semi-lexicality: Evidence from case and agreement in the nominal domain. Utrecht: Utrecht University dissertation.
Lassiter, Dan. 2017. Graded modality: Qualitative and quantitative perspectives. Oxford: Oxford University Press. DOI: http://doi.org/10.1093/oso/9780198701347.001.0001
Link, Godehard. 1983. The logical analysis of plurals and mass terms. In Bauerle, Rainer & Shwarze, Christoph & von Stechow, Arnim (eds.), Meaning, use, and interpretation of language, 302–323. Walter de Gruyter. DOI: http://doi.org/10.1515/9783110852820.302
Makri, Margarita. 2018. Aspects of comparative constructions. York: University of York dissertation.
Makri, Margarita. 2020. How many more?. In Markopoulos, Theodore (ed.), Proceedings of International Conference of Greek Linguistics 14. Patras, Greece: University of Patras.
Oikonomou, Despoina & Alexiadou, Artemis. 2021. Preverbal subjects, CLLD and inverse scope in Greek: an experimental study. In Sougari, Areti-Maria & Bardzokas Valandis (eds.), 24th International Symposium on Theoretical and Applied Linguistics – Selected Papers, 683–702. Thessaloniki: School of English, Aristotle University of Thessaloniki.
Partee, Barbara. 1989. Many quantifiers. In Powers, Joyce & de Jong, Kenneth (eds.), Proceedings of the fifth Eastern States Conference on Linguistics, 383–402. Columbus: The Ohio State University.
Pasternak, Robert & Sauerland, Uli. 2022. German measurement structures: case-marking and non-conservativity. Journal of Comparative German Linguistics 25. 221–272. DOI: http://doi.org/10.1007/s10828-022-09134-y
Rooth, Mats. 1992. A theory of focus interpretation. Natural Language Semantics 1. 75–116. DOI: http://doi.org/10.1007/BF02342617
Sassoon, Galit. 2010. Measurement theory in linguistics. Synthese 174(1). 151–180. DOI: http://doi.org/10.1007/s11229-009-9687-5
Schwarzschild, Roger. 2006. The role of dimensions in the syntax of noun phrases. Syntax 9(1). 67–110. DOI: http://doi.org/10.1111/j.1467-9612.2006.00083.x
Schwarzschild, Roger. 2012. Directed scale segments. In Chereches, Anca (ed.), Proceedings of the 22nd Semantics and Linguistic Theory Conference, 65–82. Chicago: University of Chicago. DOI: http://doi.org/10.3765/salt.v22i0.2634
Scontras, Gregory. 2014. The semantics of measurement. Cambridge, MA: Harvard University dissertation.
Solt, Stephanie. 2018. Proportional comparatives and relative scales. In Truswell, Robert & Cummins, Chris & Heycock, Caroline & Rabern, Brian & Rohde, Hannah (eds.). Proceedings of Sinn und Bedeutung 21, 1123–1140. Edinburgh: University of Edinburgh.
Stavrou, Melita. 2003. Semi-lexical nouns, classifiers, and the interpretation(s) of the pseudopartitive construction. In Coene, Martine & D’Hulst, Yves (eds.), From NP to DP. Vol. I: The syntax and semantics of noun phrases, 329–354. Amsterdam: John Benjamins. DOI: http://doi.org/10.1075/la.55.15sta
von Stechow, Arnim. 1984. Comparing semantic theories of comparison. Journal of Semantics 3. 1–77. DOI: http://doi.org/10.1093/jos/3.1-2.1
von Stechow, Arnim. 2005. Different approaches to the semantics of comparison. Ms. University of Tübingen.
Westerståhl, Dag. 1985a. Determiners and context sets. In van Benthem, Johan & ter Meulen, Alice (eds.), Generalized quantifiers in natural language, 45–71. Dordrecht: Foris Publications. DOI: http://doi.org/10.1515/9783110867909.45
Westerståhl, Dag. 1985b. Logical constants in quantifier languages. Linguistics and Philosophy 8(4). 387–413. DOI: http://doi.org/10.1007/BF00637410