1 Introduction
1.1 Overview
Understanding how learners overcome the pervasive ambiguity inherent to the language acquisition process is a foundational question of linguistics, and cognitive science more generally. In this paper, we focus on a type of structural ambiguity sometimes referred to as the Credit Problem (Dresher 1999). While this term is best known from learnability work in the Principles and Parameters framework (P&P; Chomsky 1981), the Credit Problem is inherent to any linguistic theory in which distinct structural analyses may underlie the same observed linguistic form in different contexts or languages. The Credit Problem arises when the learning data are compatible with multiple structural analyses (e.g., [kalàmatána] can be analyzed as (kalà)(matá)na or ka(làma)(tána)), and the learner must decide which analysis – and which corresponding constraint or rule in the grammar – the observed data should reinforce (e.g., Foot=Trochee or Foot=Iamb); see also Clark (1989; 1992) for early work on these concepts in P&P. There have been many proposals for how learners tackle the Credit Problem. One approach emphasizes specialized parsing mechanisms and data forms that remove or reduce ambiguity, an example of which is the well-known idea of triggers (Gibson & Wexler 1994; Berwick & Niyogi 1996; Lightfoot 1999). This approach has primarily been explored in the context of P&P syntax (Fodor 1998; Sakas & Fodor 2001; Pearl 2007; Pearl & Lidz 2009; see Sakas 2016 for an overview), although one strand of this approach – relying on domain-specific mechanisms to reduce ambiguity – has also been explored in P&P phonology (Dresher & Kaye 1990; Pearl 2007; 2011). Another approach to the Credit Problem exploits the structure of the grammatical framework, as in the classic Optimality Theoretic (OT; Prince & Smolensky 1993/2004) solution to learning rankings using Error-Driven Constraint Demotion (Tesar 1995; see also Tesar 2013 for an approach relying on the structure of Output-Driven Maps). This OT-specific approach relies on the ranking logic of winner-preferring and loser-preferring constraints and has been applied extensively in phonology (e.g., Tesar & Smolensky 1998; 2000; Pater 2010) in addition to applications in various other domains (e.g., pragmatics: Blutner & Zeevat 2004; syntax: Rodríguez-Mondoñedo 2008). A third general approach combines domain-general statistical learning strategies with theories of universal grammar. This approach has been applied extensively to constraint-based learning of hidden phonological structure (Boersma 2003; Apoussidou 2007; Jarosz 2006; 2013a; 2015; Boersma & Pater 2016; see Jarosz 2016; 2019 for overviews), and to a lesser extent in the domain of P&P syntax (Yang 2002; Straus 2008; Gould 2015). Clark’s (1989; 1992) work on genetic algorithms may also be classified under this general approach.
1.2 Domain specificity and the Credit Problem in parametric stress learning
The Principles and Parameters (P&P) approach to language typology and acquisition (Chomsky 1981) has provided important insights in both phonological and syntactic theory. In phonology, parametric models exist in the domains of word stress (Halle & Vergnaud 1987; Dresher & Kaye 1990; Dresher 1999; Hayes 1995), consonant assimilation (Archangeli & Pulleyblank 1994; Cho 1999), and syllable structure (Blevins 1995). In syntax, parametric models have been proposed for phenomena like phrase headedness, null subjects, null topics, wh-movement, nonconfigurationality, polysynthesis, X-bar phrase structure, and compounding; see Van Oostendorp (2015) and Huang & Roberts (2017) and references therein. In all of these models (except perhaps the consonant assimilation models), the parameters control hidden structure: depending on the parameter settings, different structures may be assigned to the same overt data points.
Within phonology, the Credit Problem is particularly clear in the domain of metrical stress. To succeed, the P&P learner must discover the language-specific settings of stress parameters, such as footing directionality and headedness, which are not directly observable in the language input. In this context, the Credit Problem refers to the learner’s uncertainty about which parameter setting to “credit” for a successful prediction and which to “blame” for an unsuccessful prediction. As mentioned above, to deal with the Credit Problem, existing work on stress parameter learning (Dresher & Kaye 1990; Pearl 2007; 2011) posits domain-specific learning mechanisms (see also Gibson & Wexler 1994; Berwick & Niyogi 1996; Lightfoot 1999). These are learning mechanisms that reference the contents of Universal Grammar (UG), such as feet and syllables, and thus must be specified innately as part of the language endowment. This contrasts with learning approaches in OT, where existing models rely overwhelmingly on domain-general learning strategies outside of the language endowment (see, e.g., Tesar 1995; Boersma 1997; Tesar & Smolensky 2000; Boersma & Hayes 2001; Jarosz 2013a; b; 2015; Boersma & Pater 2016).1
Contra Dresher & Kaye (1990) and Pearl (2007; 2011), we argue that a domain-general learner can successfully address the Credit Problem in parametric stress as long as it is equipped with mechanisms for performing analysis on incoming data. We propose a learning model, the Expectation Driven Parameter Learner (EDPL), that tackles the Credit Problem directly using probabilistic inference: the EDPL’s learning updates formalize “credit” as a probabilistic expression. We demonstrate that these updates can be efficiently implemented in an online, incremental learner. An “online” learner sees one data point at a time, as opposed to a “batch” learner, which sees all data simultaneously. An “incremental” learner makes small adjustments to its current hypothesis at every iteration instead of switching between radically different ones. We present systematic tests evaluating the performance of both the EDPL and a simpler learning model, the Naïve Parameter Learner (NPL; Yang 2002), on the complete typology of 302 stress systems defined by Dresher & Kaye’s 11 parameters, the first systematic tests of either model on a complete stress typology.
Our results indicate that the NPL does not possess the necessary mechanisms to cope with the pervasive ambiguity inherent to parametric stress, while the EDPL does. We conclude that domain-general learning of parametric stress remains a viable hypothesis but only if it incorporates mechanisms that directly address the Credit Problem. These conclusions have implications about the nature and content of Universal Grammar (UG), but they also complement theoretical work within and across frameworks by enriching our understanding of various theoretical frameworks’ computational properties. While our focus is on the P&P approach to metrical phonology, the learning models we examine are broadly applicable to P&P theories in phonology and beyond, and connect to current approaches to learning in Optimality Theory (OT; Prince & Smolensky 1993/2004). By contributing to the development of explicit learning models in competing frameworks, such as P&P and OT, we construct tools to help uncover differences in predictions. Conversely, computational analyses of theoretical frameworks can also uncover deep similarities between divergent approaches (for an overview of such results in phonology, see Heinz 2011a; b). Our contributions also include an in-depth discussion of how ambiguity influences learning outcomes and how that ambiguity is linked to the representational assumptions specific to each linguistic theory. The paper concludes with a discussion of how making explicit connections between learning and representational assumptions promises to yield novel empirical sources of evidence to differentiate linguistic theories.
The rest of this paper is structured as follows. We present a detailed overview of the Credit Problem in Dresher & Kaye’s (1990) word stress P&P framework (§2) and discuss the challenges it raises for existing approaches (§3). After this, the learners are discussed: the NPL, in §4 and the EDPL, in §5. In §6 we present the first systematic typological tests of both the NPL and EDPL in the stress domain, while §7 presents an in-depth analysis of the learning outcomes. Concluding remarks are offered in §8.
2 Challenges in learning parametric stress
2.1 Global and local ambiguity
Dresher & Kaye (D&K; 1990) define a set of 11 parameters of stress assignment that cover a range of typologically varied stress systems. We choose their parametric system as a concrete test case to examine the broader learning challenges posed by stress parameter setting – it is also the most concretely implementable of the available stress parameter systems (see §1). The parameters proposed by D&K and our shorthand notation (to be used henceforth) are presented in (1) below. Like most generative linguistic systems of any complexity, this system of 11 parameters results in surface patterns with widespread ambiguity, as discussed by D&K.
| (1) | i. | The word-tree is strong on [Left/Right] (Main=Left/Right) |
| ii. | Feet are [Binary/Unbounded] (Bounded=On/Off) | |
| iii. | Feet are built from the [Left/Right] (Dir=L-to-R/R-to-L) | |
| iv. | Feet are strong on the [Left/Right] (Foot=Trochee/Iamb)2 | |
| v. | Feet are quantity sensitive (QS) [Yes/No] (QS=On/Off) | |
| vi. | Feet are QS to the [Rime/Nucleus] (CVC=Light/Heavy) | |
| vii. | A strong branch of a foot must itself branch [No/Yes] (HeavyHead=On/Off) | |
| viii. | There is an extrametrical syllable [No/Yes] (XM=On/Off) | |
| ix. | It is extrametrical on the [Left/Right] (XMdir=Left/Right) | |
| x. | Feet consisting of a single light syllable are removed [No/Yes] (Degenerate=On/Off) | |
| xi. | Feet are noniterative [No/Yes] (SecStress=On/Off) |
For D&K, bounded feet can have the shapes {(L), (LL), (H), (HL), (LH)}. Feet of the shape ( L) are allowed (contra Hayes 1995). Parameter (1vi) only matters if QS=On; if QS=Off, all syllables are treated as light, even when CVC=Heavy. Similarly, parameter (1ix) only matters if XM=On; if XM=Off, the setting of XMdir does not matter.2
L) are allowed (contra Hayes 1995). Parameter (1vi) only matters if QS=On; if QS=Off, all syllables are treated as light, even when CVC=Heavy. Similarly, parameter (1ix) only matters if XM=On; if XM=Off, the setting of XMdir does not matter.2
When HeavyHead=On, then after feet are constructed, all feet with light syllable heads are deleted, as in LLHLH → (ĹL)( L)(
L)( ) → LL(
) → LL( L)(
L)( ). In a quantity-insensitive language, all syllables are light, and thus, all feet are deleted. When Degenerate=On, all feet consisting of one light syllable are deleted; in this, we follow Dresher (1999); D&K’s original formulation of (1x) is slightly different and somewhat underspecified: “A weak foot is defooted in clash”. Secondary stress feet are always constructed, but when SecStress=Off, the heads of non-main feet do not project stress (D&K’s original name for this parameter, Noniterativity, is somewhat misleading). This means that when SecStress=On, all feet have stress.
). In a quantity-insensitive language, all syllables are light, and thus, all feet are deleted. When Degenerate=On, all feet consisting of one light syllable are deleted; in this, we follow Dresher (1999); D&K’s original formulation of (1x) is slightly different and somewhat underspecified: “A weak foot is defooted in clash”. Secondary stress feet are always constructed, but when SecStress=Off, the heads of non-main feet do not project stress (D&K’s original name for this parameter, Noniterativity, is somewhat misleading). This means that when SecStress=On, all feet have stress.
The most ambiguous stress pattern in D&K’s framework is initial/final stress. A form with initial stress, as in (2), could be attributed to settings of completely unrelated parameters, corresponding to distinct assignments of hidden structure, as illustrated in (2a–c). In (2a), binary trochees are built throughout the word, of which the leftmost receives main stress, with no overt stress projected from the other trochees. In (2b), a single unbounded trochee is built over the entire word, and it receives main stress; note that this is consistent with Main = Left or Main = Right. In (2c), no feet are built because HeavyHead=On requires that all foot heads be heavy, while all available syllables are light because of QS=Off. Since Main=Left, the leftmost element (here, the leftmost syllable) is assigned main stress. This example involves global ambiguity: no further data from the same stress system will disambiguate between the various hypotheses in (2) since they all predict initial stress for words of any length and syllable structure. Acquiring any of these three settings may be considered as correctly acquiring the language.
| (2) | a. | (σ́σ)(σσ)(σσ) |
| Foot=Trochee, Main=Left, SecStress=Off | ||
| b. | (σ́σσσσσ) | |
| Foot=Trochee, Bounded=Off | ||
| c. | σ́σσσσσ | |
| Main=Left, QS=Off, HeavyHead=On |
In (2), the three sets of parameter settings are compatible with one another: combining any of these three settings will also yield initial stress. In other cases, structural analyses of the same overt stress pattern can be mutually incompatible. The pattern with penultimate main stress and alternating secondary stress provides an example, as shown in (3) for odd-syllable words and (4) for even-syllable words. In the iambic parses in (3a) and (4a), Right-to-Left iambic feet are built with right extrametricality such that degenerate feet are allowed, and the rightmost foot receives main stress. In (3b) and (4b), Right-to-Left trochaic feet are built without extrametricality and degenerate feet are disallowed. This is also global ambiguity since both types of parses yield the same stress patterns for all words. However, here the learner must find a consistent combination of several interdependent parameters to produce the right stress pattern. If the learner chooses trochees, it must also posit no extrametricality and no degenerate feet; if it chooses iambs, it must also posit right extrametricality and permit degenerate feet.
| (3) | a. | (σσ̀)(σσ́)<σ> |
| Foot=Iamb, Dir=R-to-L, XM=On, Degenerate=On | ||
| b. | σ(σ̀σ)(σ́σ) | |
| Foot=Trochee, Dir=R-to-L, XM=Off, Degenerate=Off |
| (4) | a. | (σ̀)(σσ̀)(σσ́)<σ> |
| Foot=Iamb, Dir=R-to-L, XM=On, Degenerate=On | ||
| b. | (σ̀σ)(σ̀σ)(σ́σ) | |
| Foot=Trochee, Dir=R-to-L, XM=Off, Degenerate=Off |
Such cases of global ambiguity require learners to be sensitive to the interdependence between parameters: the learning data will never provide unambiguous information about the settings of some parameters. In (3–4), both odd- and even-parity words are compatible with trochees and iambs: there is no learning data that will unambiguously require one or the other foot type. The same holds for the extrametricality, directionality and degenerate foot parameters.
In addition to global ambiguity, the learner must also cope with local ambiguity – ambiguity in the analysis of a particular data point that must be resolved, but requires reference to other data points. Many data points are uninformative for setting a particular parameter. For instance, words consisting only of light syllables are compatible with all four possible settings of the quantity-sensitivity parameters. Similarly, words with an even number of (non-extrametrical) syllables are consistent with both Left-to-Right and Right-to-Left footing.
The learner must be able to combine information across multiple data forms to arrive at a grammar that accounts for all observed stress patterns. For example, a language with antepenultimate main stress and alternating leftward secondary stresses (e.g., [ta.mà.na.pò.la.tú.ti.la]) must be analysed with Right-to-Left trochees and right extrametricality. However, each individual word has an alternative analysis with Left-to-Right trochees. For even-parity words like <na>(pò.la)(tú.ti)la, this Left-to-Right analysis requires left extrametricality, whereas odd-parity words like (mà.na)(pò.la)(tú.ti)la require no left extrametricality. It is only by comparing even-parity and odd-parity words that the learner can conclude that the correct analysis is indeed Right-to-Left. Note, this conclusion also requires sensitivity to the interdependence between parameters since it depends on identifying a consistent setting of the extrametricality parameters which, in combination with the directionality setting, produces the correct stress pattern across all forms.
Thus, learning parametric stress requires facing ambiguity resulting from two types of interdependence: interdependence between parameters and interdependence between word forms. The data may be globally ambiguous and require the learner to commit to a combination of interdependent parameter settings to specify a working grammar. Moreover, a given learning datum may be locally ambiguous and require the learner to cope with interdependence between data forms to set crucial parameter settings. This results in a difficult computational challenge since the learner cannot solve the problem by considering parameters or data points in isolation. Such ambiguities, especially the one in (3), are also relevant in other frameworks like Hayes (1995) or OT approaches like Tesar & Smolensky (2000), but we use D&K’s framework as a case study.
2.2 The Credit Problem
Interdependencies like these are a challenge for an incremental learner. When the learner’s current hypothesis correctly generates the stress pattern for an observed word, the learner faces the Credit Problem: it is unclear which parameter setting to credit with this correctness. For example, if the learner’s current grammar generates (σσ̀)(σσ́) with Right-to-Left iambs, matching the observed pattern σσ̀σσ́, the learner does not know whether it is iambic footing or Right-to-Left directionality that should get credit for this match. The same problem occurs when the model fails to generate the correct stress pattern. For example, if the observed pattern is σσ̀σσ́ and the learner’s current grammar produces the mismatching <σ>(σ́σ)σ, it is not immediately obvious whether left extrametricality, the presence of extrametricality, the trochaic foot, or the lack of degenerate feet led to the mismatch between the observed and the predicted stress pattern. Simply observing that a combination of parameter settings leads to a match or mismatch does not mean that all parameter settings should share credit or blame equally.
To address the Credit Problem, the learner must have a way to gauge which parameters are the most relevant to and responsible for a given data point. Not only must the learner resolve this ambiguity and ultimately succeed in reaching the target grammar, it must do so using a computationally feasible learning procedure. In addition to considering learning success, in this paper we consider two fundamental measures of computational complexity. Processing complexity refers to time spent computing a learning update for an individual datum and data complexity refers to the number of data forms needed to reach the target grammar. Both must be feasible for the overall learning process to be feasible. In the next section, we review some possible strategies for coping with the Credit Problem and dealing with the interdependencies inherent to learning parameter settings discussed above.
3 Strategies for coping with ambiguity and the Credit Problem
Given the preceding discussion, it should be clear that brute-force approaches cannot cope with the computational challenges inherent to learning parameter settings from structurally ambiguous data, as has been discussed extensively in previous work (D&K 1990; Fodor 1998; Dresher 1999; Yang 2002; Pearl 2011; Gould 2015). For example, Fodor (1998) discusses a strategy in which the learner considers all combinations of all parameter settings for each learning datum to discover all successful analyses of the datum. The parameters that have a consistent setting across all successful analyses are crucial to that datum, and the learner sets those parameters in their grammar. Data points that provide crucial evidence for the setting of some parameter – because they are consistent with only one setting – are called triggers for that parameter (Gibson & Wexler 1994; Berwick & Niyogi 1996; Lightfoot 1999). With this capacity to identify triggers, this learner could gradually accumulate evidence about individual parameter settings, gathering whatever information each individual datum provides. It would therefore provide a way to cope with some cases of local ambiguity.
Unfortunately, this strategy has two fatal flaws. First, as Fodor points out, explicitly enumerating all combinations of all parameter settings for each datum is computationally intractable: the processing complexity grows exponentially with the number of parameters. Second, this strategy would fail to learn a complete grammar in cases of global ambiguity like examples (2–4). There, successful analyses of the learning data vary on all settings of numerous parameters: no single parameter setting is shared between them, and no datum in the language can help this learner break out of the ambiguity. In other words, the data are not guaranteed to contain triggers for every parameter. For extensive discussion of this issue in the domain of syntactic parameters, see Gibson & Wexler (1994). Examples (2–4) highlight the point that lack of triggers is not an issue specific to syntax, but rather a general challenge for learning parameter settings. Thus, this strategy fails to cope with interdependencies between parameters.
In the domain of stress, several learning models for parameter setting have been proposed and can be broadly classified either as domain-specific or domain-general. Both domain-specific and domain-general learning approaches assume UG is available to the learner: the learner has access to the universal set of parameters, their possible settings, and the system that generates linguistic structures based on specified parameter settings. They differ, however, in whether the posited learning mechanisms are domain-specific themselves.
Domain-specific learners for parameters may have prior knowledge of ambiguities that arise for linguistic data for a particular set of parameters, the best order in which to set these parameters, and/or default settings of these parameters (Pearl 2007). These mechanisms do not generalise beyond the specified grammatical system – they are intrinsically tied to particular parameters.
In contrast, domain-general learners, while having access to UG and being able to manipulate parameters, have learning strategies that do not depend on the content or identity of any specific parameter (domain-specific knowledge). Crucially, a domain-general learner cannot rely on the identity of a parameter to make inferences about its setting or connect it to data. Domain-general learners rely on mechanisms that generalise beyond a given system or linguistic domain.
3.1 Domain-specific hypotheses
In the domain of stress, one well-known domain-specific learning approach relies on cues to parameter setting (D&K 1990; Pearl 2011). Cues are overt data patterns that identify triggers for a particular parameter setting or group of parameter settings. Each parameter is hypothesised to be associated with a cue for at least one setting, and one setting may be specified as default.
Cues tell the learner which data points are informative for a given parameter setting. For instance, if we again consider the example of ambiguity in initial-stress words like σ́σσσσσ (see (2) in §2.1), cues can tell the learner that this data point is uninformative for many different parameters. D&K (1990) propose that QS=Off by default and is only overturned if the learning data contain a pair of words with the same length in syllables but different stress patterns.3 D&K specify that QS=Off is incompatible with Bounded=On and HeavyHead=On, which means that if there is no evidence for QS=On, these parameters will be set to Bounded=Off and HeavyHead=Off, respectively.4 However, if QS=On, the learner assumes that Bounded=Off until it encounters a stressed light syllable away from the word edge. Similarly, if QS=On, the learner presumes HeavyHead =On until it sees a stressed light syllable away from the word edge or a light syllable with secondary stress. Finally, the learner presumes that SecStress=Off until it encounters a data point with secondary stress. Word-initial stress in σ́σσσσσ does not fit the cues for QS or SecStress. If all words in this language have initial stress, the learner will decide that this language is quantity-insensitive (QI) with bounded feet, HeavyHead=Off, and no overt secondary stress, as in (2a). The combination of default settings and cues lets the learner circumvent the interdependencies between parameters and between data points discussed above. Notably, this learning strategy commits the learner to a particular analysis of a globally ambiguous pattern. Although the parametric system can represent the other analyses, they will never be selected by a learner with these cues and defaults. In contrast, the domain-general learners explored in §§4–7 must cope with all analyses of such patterns.
In addition to cues for each parameter, D&K specify an order in which parameters should be acquired.5 This is another way in which domain-specific learners can cope with interdependencies between parameters. For instance, the cue for Bounded=On is the presence of stressed non-peripheral light syllables. To determine whether a syllable is light and non-peripheral, the learner first needs to know which syllables are heavy in the language (determined by the two QS parameters) as well as which syllables are peripheral (determined by the two extrametricality parameters). For this reason, D&K posit that the acquisition of foot (un)boundedness occurs after the acquisition of quantity-(in)sensitivity and (non-)extrametricality.
Gillis et al. (1995) tested D&K’s learner on all 216 parameter specifications with Degenerate=Off permitted in D&K’s original framework and found that 173 (80.1%) of these were correctly learned. Gillis et al. only considered words of 2–4 syllables; Dresher (1999: 40fn11) hypothesizes that considering longer words will lead to a greater success rate; however, effectiveness comparisons between D&K’s learner and domain-general strategies do not yet exist.
More recently, Pearl (2007) examines both domain-general and domain-specific strategies for learning English stress. She shows that only some parameter orders lead to successful learning of stress parameters in English, assuming a parameter is set when more data points unambiguously support that setting compared to the opposing setting. Pearl concludes from this that either cues or a pre-determined order of setting parameters are necessary for acquiring English stress. Pearl (2011) also shows that several versions of the domain-general Naïve Parameter Learner (NPL; Yang 2002) overwhelmingly fail to find the desired analysis of English stress. Based on these considerations, she argues domain-specific mechanisms are essential.
Thus, Pearl’s arguments are based on a direct comparison of domain-specific and domain-general learning strategies, but the argument focuses on one analysis of one language. D&K propose a parametric system and a detailed domain-specific learning model for that system, but they do not explore alternative models with weaker assumptions. This is the question we undertake in this paper by systematically evaluating two domain-general learning models on D&K’s typology.
3.2 Domain-general hypotheses
Domain-general approaches have not been extensively explored in the domain of stress parameter learning. Beyond our own proposal, the only application of domain-general learning models to parametric stress is the series of studies by Pearl (2007; 2011) discussed above examining the learning of English stress using the NPL (Yang 2002).
The NPL is an online, incremental learning algorithm for probabilistic P&P grammars, the details of which are presented in §4. The algorithm is naïve in the sense that no attempt is made to address the Credit Problem directly. No analysis of the learning data is performed: no attempt is made to determine which parameters are crucial, which are incompatible, nor which are irrelevant for the observed data. As acknowledged by Yang (2002), this can lead to incorrect updates and inconsistencies during learning.
Pearl (2011) proposes a variant of the NPL (based on a similar proposal in Yang 2002), which we call “pseudo-batch” here, which is described in §4.3 and aims to limit the potential harmful effects of such inconsistencies. A conceptually similar method of smoothing is to use a Bayesian update rule (Pearl 2007; 2011; Gould 2015), where previous data points’ propensity towards a particular parameter setting increases or decreases the influence that the current data point’s preference for a parameter setting has on the grammar. Pearl finds some improvement in performance using the pseudo-batch variant of the NPL, but ultimately concludes that neither adding pseudo-batch learning, nor adding a Bayesian update rule (nor both) is sufficient to consistently learn English stress. In the simulation results presented in §6.2, we show that, while pseudo-batch learning increases the success rate of the NPL, it still does so in a very limited fashion.
3.3 Discussion
To summarise, the most prominent and extensively studied approaches to the Credit Problem in stress parameter learning rely on domain-specific learning mechanisms. Existing work on domain-general learning of stress (Pearl 2011) is limited to one language (English) and one learning model (NPL).
Domain-specific approaches have a number of drawbacks. One is the strong assumptions made about the genetic endowment, since they assume domain-specific knowledge beyond the knowledge of UG itself. Tesar & Smolensky (1998: 255–257) discuss several additional challenges for the domain-specific approach. The learning model proposed by D&K is entirely specific to their parameters. The learning model cannot be applied to any other stress parameter system or linguistic domain, let alone to another cognitive domain. This also means the predictions of the learning model are entirely dependent on the particular linguistic analysis made possible by this parametric system. It is therefore not possible to compare learning of two parametric systems, or two analyses of the same phenomena, with the same domain-specific learning model. Since the theory of grammar and of learning are inextricably linked, learning cannot provide independent evidence for or against theoretical choices.
Domain-general approaches do not share these disadvantages. The assumptions about the genetic endowment are more modest, and a domain-general model tested on one parametric system can be applied without modification to any other parametric system, whether that be an alternative theory of stress parameters or a parametric system in another domain, such as syntax.
In the rest of this paper, we show the possibilities of domain-general learning in D&K’s parametric stress framework. Before presenting our novel approach in §5, we first explain how the NPL works, with which our proposal shares all but one aspect of its inner workings.
4 The Naïve Parameter Learner (Yang 2002)
Yang (2002) proposes a domain-general statistical learner for parameter systems, the Naïve Parameter Learner (NPL), based on criteria of minimal cognitive load and gradualness: the property of incrementally transitioning from one grammar state to the other. This approach has been held as a benchmark of learning parameter grammars (Sakas 2016) and has a proof of convergence that holds under certain strict conditions (Straus 2008).
The novel proposal in the current paper, the Expectation Driven Parameter Learner (EDPL, see §5), shares the majority of its machinery with the NPL: the probabilistic parameter grammar framework and the linear update rule, which will be discussed in §4.1 and §4.2, respectively. The difference between the learners lies in how the reward/penalty value in the update rule is calculated. The NPL’s method for doing so is covered in §4.2 (see §5 for the EDPL’s method). Then, a pseudo-batch modification to the NPL is presented in §4.3, while §4.4 presents some crucial challenges for the NPL.
4.1 Probabilistic parameter grammars
Yang defines a probabilistic parameter grammar in terms of a set of independent Bernoulli distributions, one for each (binary) parameter in UG, as exemplified in (5). The probability of a parameter setting stands for how often this setting will be chosen at a given instance of the grammar’s use. The probabilities of the settings for each parameter sum to 1, and there is no relationship between the probabilities of settings of different parameters.
| (5) |
When a grammar is used to generate an output for a given input (in our case, a stress pattern given a sequence of syllables), each parameter is given a categorical setting sampled from that parameter’s probability distribution. An output is then generated based on the parameter specification generated in this way (cf. (6)).
When learning, this predicted output is compared to an observed output, resulting in a stress match or mismatch. In (6), two parameter specifications are generated from the grammar in (5). In (6a), rightmost main stress and L-to-R feet are selected, while in (6b), leftmost main stress and R-to-L feet are selected. Because of the probabilities in the grammar, the specification in (6b) is more likely to be chosen than the one in (6a). In both cases, feet are bounded, since this option has a probability of 1 in the grammar. In terms of production and comparison to the hypothetical observed forms, the specification in (6a) leads to a match between the predicted and the observed stress pattern, while the specification (6b) leads to a mismatch.
| (6) | a. | Sample parameter specification 1: Main=Right, Bounded=On, Dir=L-to-R, … | ||
| probability: 0.4 × 1 × 0.3 = 0.12 | ||||
| (kàla)(máta)na | observed: [kàlamátana] | match=TRUE | ||
| b. | Sample parameter specification 2: Main=Left, Bounded=On, Dir=R-to-L, … | |||
| probability: 0.6 × 1 × 0.7 = 0.42 | ||||
| ka(láma)(tàna) | observed: [kàlamátana] | match=FALSE | ||
Both the NPL and the EDPL represent their knowledge of language in terms of Yang-style grammars. If the stress system of a language is categorical, with no variation between or within words, this can be represented by a grammar where all crucial parameter settings have a probability of 1. However, if a language does exhibit variation, it is possible to represent this by giving parameter settings probabilities between 0 and 1. In this paper, we only consider categorical systems as targets of learning, but patterns with variation are an important intermediate stage, and target patterns with variation are an important test case for future work.
4.2 Linear update rule
Both the NPL and EDPL use the Linear Reward-Penalty Scheme (LRPS; Bush & Mosteller 1951), see our formulation in (7), to update grammars in the course of learning. This online update rule uses what we call a Reward value, a value between 0 and 1, to adjust each parameter setting’s probability higher or lower. The LRPS simply takes a weighted average of this Reward value and the old probability of a specific parameter setting, π = υ, to compute a new probability for that setting.
| (7) |
Where:
P(π = υ │Gt) is the parameter setting’s probability in the grammar at time t
R(π = υ)∈[0,1] is the parameter setting’s current Reward value
λ∈[0,1] is the learning rate
For the NPL, each parameter’s Reward value is either 0 or 1, with no intermediate values. This value is determined based on a single parameter specification sample, St, selected at time t from the current grammar to generate an output to compare against the current data point’s stress pattern, as in (8). A parameter setting’s Reward value is 1 if that setting is in the specification and the specification results in a match, or if the setting is not in the specification while the specification results in a mismatch. Otherwise, the Reward value is 0.
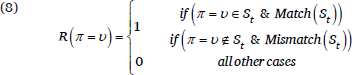
For example, consider scenario (6a). Main=Right is in specification St={Main=Right,Bounded=On,Dir=L-to-R,…} and St matches [kàlamátana], so according to the first clause in (8), R(Main=Right)=1. Main=Left is not in St, but St does yield a match, so neither condition for a reward value of 1 applies, meaning that R(Main=Left)=0. Assuming a learning rate of 0.1, the updated probability of Main=Right would be P(Main=Right)=0.1 × R(Main=Right) + 0.9 × 0.4 = 0.46, increasing from 0.4 to 0.46. All the parameters in the grammar would be similarly updated based on this match – for instance, Bounded=On would be rewarded (in St and match so R=1) and Bounded=Off would be penalized (not in St and match so R=0). When there is a mismatch, as in (6b), the sampled parameter settings receive R=0 (e.g. Main=Left), while the opposite settings receive R=1 (e.g. Main=Right).
The NPL fares exceedingly well on processing complexity. For each data point, it takes one sample for each parameter, and uses the resulting match or mismatch to compute which settings get rewarded and which get penalised. The time complexity grows linearly with the number of parameters: each additional parameter in the grammar requires a constant amount of additional computation for the processing of one data form. In §6, we present tests that investigate the NPL’s data complexity and success rates.
4.3 Pseudo-batch learning
As discussed earlier, Pearl (2011) reformulates Yang’s “batch” NPL variant, positing an algorithm to help smooth out learning across data points. This is not an actual batch learning algorithm, but a modification of the online update procedure of NPL, which is why we call it “pseudo-batch”. The probability of a particular parameter setting is updated only once recent data points preferring this setting outnumber those preferring the opposite setting by a prespecified threshold. To do this, the learner keeps a counter for each parameter setting, initialized to zero. If the counter reaches the positive threshold, this parameter setting’s probability in the grammar is updated with a Reward value of 1, and if it reaches the negative threshold, that parameter setting’s probability is updated with a Reward value of 0. After each update, the counter for this parameter setting is reset to 0. The counters for all other parameters remain unaffected.
The result of this pseudo-batch procedure is that parameter settings that work for certain words but not others are less likely to be rewarded, since their successes may be offset with immediately following failures, leading to a counter vacillating around 0. On the other hand, parameter settings that are crucial for the target language are more likely to be successful in succession, leading to a rapidly rising counter and a Reward value of 1 in many cases. However, this does not guarantee finding all crucial parameter settings due to the accomplice scenario explained in §4.4.
We examine the effect of pseudo-batch learning in the simulations in §6, comparing the NPL with and without pseudo-batch learning side-by-side.
4.4 Challenges for the NPL
Yang (2002) acknowledges that the NPL does not attempt to address the Credit Problem directly and names two specific ways in which the Credit Problem can manifest itself in the NPL: hitchhikers and accomplices. Yang (2002: 43) explains that the “hope” behind NPL is that the gradual, statistical nature of the learning process will allow the learner to smooth over these inconsistencies while allowing the crucial parameter settings to rise to dominance over time; however, our results in §6 show that is not the case for the stress parameter setting problem.
In the hitchhiker scenario, parameter settings are rewarded despite having no responsibility for a match. For example, suppose the learner observes the data point [kàlamátana] (cf. (6)) and generates its output using a parameter specification that contains the crucial setting Main=Right as well as a setting that is irrelevant to this data point, like QS=On (irrelevant since there are no heavy syllables). The combination of these parameter settings leads to a match to the observed stress. Since the NPL rewards every parameter setting involved in generating a match, the crucial setting, Main=Right, is rewarded, and the irrelevant setting, QS=On, “hitchhikes” along and also receives a reward of the same magnitude, even though QS=On has no role in creating the current stress match and may be inconsistent with the data set at large.
In the accomplice scenario, parameter settings are penalised despite not being responsible for a mismatch. Consider again the data point [kàlamátana], and suppose the learner samples a parameter specification from their grammar with the crucial setting Main=Right and the incompatible setting Bounded=Off, which is incompatible since an unbounded foot over light syllables yields only one stress. This results in a mismatch: the secondary stress in [kàlamátana] is not generated. Because the NPL penalises all parameter settings in a specification that results in a mismatch, it not only penalises the incompatible setting Bounded=Off, but also the crucial setting Main=Right, which is an “accomplice” in creating an incorrect stress form. This is problematic, because Main=Right is needed to obtain the correct stress for this datum, so it should have been rewarded rather than punished.
Because of the widespread ambiguity in stress setting discussed earlier, hitchhikers and accomplices can lead to serious challenges for the model. The same parameter setting can be rewarded by accident for one data point and penalised by accident for the next data point. These spurious updates create substantial noise that disrupts the learning process. As discussed above, the pseudo-batch strategy may smooth over some of this noise, and we consider its effects on the performance of the model in §6.
More problematic than random noise is the general failure of the model to cope with interdependence between parameters, which is the underlying source of accomplices and hitchhikers in NPL. A crucial parameter setting only leads to a match with the data if all other crucial parameters for that data point are set appropriately for the target language. Unless the learner’s grammar is already very close to the target grammar, sampling the correct combination of all crucial parameter settings is a statistically rare occurrence. This means that the vast majority of updates are mismatches involving spurious penalties for crucial parameter settings (accomplices), causing the learner to make no progress, vacillating endlessly until they happen to sample a correct combination of all crucial parameter settings to reward (in which case they are at risk of rewarding hitchhikers). However, it is possible to design a domain-general learner that overcomes these challenges, as shown in §5, where we propose the Expectation Driven Parameter Learner, which addresses the Credit Problem directly in the formulation of the Reward value.
5 Proposal: The Expectation Driven Parameter Learner
The EDPL model proposed here extends Jarosz’s (2015) Expectation Driven Learning proposal developed for probabilistic OT. It maintains the same type of probabilistic grammar as the NPL without using any additional memory, it uses the same online update rule (LRPS, see (7)) after each data point presented to the learner, and, like the NPL, its processing complexity grows slowly with the number of parameters. The difference between the two models lies in the Reward values computed. The EDPL gives each parameter setting a separate Reward value proportional to its responsibility in generating the current data point. For instance, for [kàlamátana] (cf. (6)), Main=Right is a crucial setting, QS=On is an irrelevant setting, and Bounded=Off is an incompatible setting, all of which are rewarded differently by the EDPL. This avoids hitchhikers and accomplices: irrelevant QS=On is not rewarded for co-occurring with Main=Right, whereas the latter is not punished for co-occurring with Bounded=Off.
Formally, the Reward is defined as the expected value of a parameter setting given the current grammar and the data point currently under examination. Computing this value relies on two crucial steps (Jarosz 2015): estimating the probability of the current data point given each parameter setting using constrained sampling, and then converting this probability into the Reward value using Bayes’ Rule. The following subsections walk through these steps in detail.
5.1 Defining the Reward
Rather than updating all parameters equally, the EDPL defines the Reward value R(π = υ) for parameter setting π = υ as the probability of that parameter setting given the current data point and the current grammar, (9a). Intuitively, this quantity represents that parameter setting’s responsibility in generating the observed stress pattern – the probability of finding that parameter setting among the successful parses of the observed learning datum. Once the reward value is computed, it is plugged into the same update rule used by NPL, repeated in (9b).
| (9) | a. | |
| b. |
Rather than computing the probability in (9a) directly using parsing, we follow Jarosz (2015) in decomposing this expression using Bayes’ Rule into three quantities (10a) that can be easily estimated using the production grammar. The first term, P(match|π = υ,Gt), is the conditional likelihood that a given parameter setting leads to a match with the current data point and can be estimated efficiently using constrained sampling from the production grammar, as described in §5.2. The second term, P(π = υ|Gt), is simply the probability of that parameter setting in the current grammar and can be looked up directly. Once these quantities are computed for both settings of a parameter, the denominator can be computed by plugging these quantities into the marginalization formula in (10b): the probability of a match given this parameter is a weighted sum of the match probabilities of both of its settings.67
| (10) | a. | |
| b. |
Defining the Reward value this way yields an online, sampling-based approximation to Expectation Maximization (EM; Dempster et al. 1977): instead of setting the new probabilities of parameter settings to their expected values given the entire data set, which would be the classic EM approach, the process here is broken up into smaller and more local calculations computed incrementally on each incoming data point, just like in the NPL. The EDPL update rule moves the probability of π = υ closer to its expected value given the current data point.
5.2 Sampling: correct stress given parameter setting
We use constrained sampling from the production grammar to estimate the conditional likelihood P(match|π = υ,Gt) following Jarosz (2015). To perform this sampling, the current parameter grammar, Gt, is temporarily modified by replacing the probability of parameter setting π = υ with 1 and replacing the probability of the opposing setting of the same parameter with 0. This temporary grammar in which every production is guaranteed to choose parameter setting π = υ provides an estimate of π = υ’s contribution to matching the current data point. For this estimate, a fixed number r of samples is taken by repeatedly generating an output for the current data point with that temporary grammar, and assessing the number of matches that result. P(match|π = υ,Gt) is then estimated by dividing the number of matches by the number of samples, see (11). The analogous computation is then performed for the other setting of that parameter: π = ¬υ (cf. the second term of (10b)).
| (11) |
During this process, the probabilities for the other parameters are left untouched. This makes it possible to isolate the effects of manipulating a single parameter. At the same time, using the full production grammar ensures that the consequences of any interactions with other parameters are taken into account.
To summarise, the EDPL computes a separate Reward value for each parameter setting (e.g., for the grammar in (5): Main=Left/Right, Bounded=On/Off, Dir=L-to-R/R-to-L) given a data point (e.g., [kàlamátana]). This involves creating two temporary grammars, one for each setting of the parameter (e.g., when looking at Main, we have temporary grammars Gt,Main=Left={P(Main=Left)=1, P(Bounded=On)=1, P(Dir=L-to-R)=0.3} and Gt,Main=Right={P(Main=Left)=0, P(Bounded=On)=1, P(Dir=L-to-R)=0.3}), sampling from each a fixed number of times (e.g., if r=5, Gt,Main=Left might generate {kálamàtana,kalámatàna, kalámatàna,kálamàtana,kalámatàna} and Gt,Main=Right might generate {kàlamátana,kalàmatána,kalàmatána,kàlamátana,kalàmatána}), and calculating the probability of a match according to (11) (0/5=0 for Main=Left, 2/5=0.4 for Main=Right). These values are then plugged into (10ab): R(Main=Left)=P(Main=Left|match,Gt)=0/(0+0.4)=0, R(Main=Right) =P(Main=Right|match,Gt)=0.4/(0 + 0.4) = 1.8 The processing complexity for the EDPL is greater than the NPL: the grammar is sampled 2r times per parameter rather than once. This means the overall processing complexity grows quadratically with the number of parameters: each grammar sample requires walking through all the parameters, and this must be done a fixed number of times for each parameter. However, quadratic processing time is still very efficient and certainly much more efficient than exhaustive search as the number of parameters increases. We examine data complexity of both the EDPL and the NPL in more detail in §6.
5.3 EDPL approach to the Credit Problem
The EDPL provides a principled solution to the Credit Problem without domain-specific mechanisms. It distinguishes necessary, incompatible, and irrelevant parameter settings by computing Reward values separately for each parameter setting, where Reward values are defined as the degree to which each parameter setting is responsible for each data point.
A parameter setting necessary for data point d (e.g., Main=Right for [kàlamátana] in (6)) will always have a Reward value of 1 since the probability of generating the data point with the opposing parameter setting is 0, as shown in (12a), even if the necessary parameter setting sometimes yields mismatches (e.g., Main=Right is compatible with [kalàmatána]): see footnote 8. The numerator and denominator simplify to the same value, yielding 1. The update rule will thus always give a crucial parameter setting a maximal increase in probability when that data point is processed.
Conversely, a parameter setting that is incompatible with data point d (e.g., Bounded=Off for [kàlamátana]) will always have a Reward value of 0, as in (12b), since the probability of generating a match using an incompatible parameter setting is 0, making the numerator 0. The update rule will thus always give an incompatible parameter setting a maximal decrease in probability.
Finally, for a parameter setting irrelevant to data point d (e.g., QS=On for [kàlamátana]), its Reward value will be roughly equal to its probability in the grammar. Such a parameter setting has no effect on generating a match: either setting of this parameter will on average produce the same proportion p of matches with the data point. As shown in (12c), replacing the conditional likelihoods for both parameter settings with p results in an expression that simplifies to the probability of the irrelevant parameter setting in the current grammar. In this case, the update rule in (9b) produces no change to the parameter’s probability. This means that whenever the model encounters a parameter setting that is irrelevant to the current data point, the grammar remains unaffected by this data point. In all three cases, this is the desired behaviour: crucial parameter settings should be consistently rewarded, incompatible parameter settings should be consistently penalised, and irrelevant parameter settings should remain unchanged.
| (12) | a. | Parameter setting crucial for data point d: |
| b. | Parameter setting incompatible with data point d: | |
| c. | Parameter setting irrelevant to data point d: | |
It must be stressed that the three updated scenarios discussed above are only the edge cases. As discussed in §2, stress parameters are often ambiguous: multiple parameter settings are potentially compatible with the same data point. It is in such cases that EDPL Reward values other than 1, 0, or P(π = υ) are found.
The EDPL relies on the learner’s current knowledge of one parameter to make inferences about settings of other, interdependent parameters to deal with such ambiguous cases. For example, suppose the learner’s current grammar has P(Dir=R-to-L)=0.7 and P(XM=On)=0.5: that is, the learner is completely uncertain about extrametricality, but it believes Right-to-Left directionality is more likely than Left-to-Right. If the learner then observes [kàlamátana], a data point that is ambiguous in terms of both extrametricality and directionality, it will be able to use its current knowledge of directionality to make inferences about extrametricality from this ambiguous data point: it will reward XM=On. This occurs because the sampling procedure is sensitive to the other settings in the grammar. Left-to-Right is compatible with either setting of extrametricality, but because this grammar selects Right-to-Left more often, and Right-to-Left only generates the correct pattern when extrametricality is on, XM=On will be more successful than XM=Off. This example demonstrates the EDPL’s capacity to deal with local ambiguity not only in the categorical edge cases, but also in contexts where previously accumulated knowledge about one parameter gradiently affects the learner’s inferences about another.
6 Typological test of the NPL and EDPL
In this section, we will present systematic evaluations of the NPL and the EDPL on a diverse range of stress systems, constituting the first systematic typological test for these learners in the stress domain. Our primary goal is to gauge how well these models cope with the Credit Problem and the kinds of interdependencies that are inherent to parametric stress systems. By considering both models’ performance on the full typology proposed by D&K (1990), we get the most complete picture possible regarding their capacities to deal with hidden structure in a complex stress parameter system. This kind of evaluation is analogous to Tesar & Smolensky’s (2000) typological tests of their hidden structure learner on a set of 124 stress systems, a varied subset of the languages generated by their constraint set, which was later used by Boersma (2003); Boersma & Pater (2016); and Jarosz (2013a; b) to evaluate other learning models. We present two quantitative measures of performance, discussed in more detail below, which provide a first step in determining the viability of these learning models on complex stress parameter learning. To evaluate the capacity of these models to succeed at learning, we report success rates on the full typology, and to assess the models’ data complexity, we report time-to-convergence statistics. Additionally, these typological tests allow us to analyse the properties of stress systems that are particularly challenging and particularly straightforward for the models to learn, leading to a deeper understanding of the general predictions these models make for learning beyond this particular framework.
6.1 Structure of the typology
The 11 stress parameters defined by D&K together define 211 = 2048 unique parameter specifications. To complement the discussion of ambiguity in §2, here we introduce a quantitative measure of ambiguity and use it to examine the rate and distribution of ambiguity in the typological space defined by these parameters. This measure provides a richer characterization of the types of ambiguities present in parametric systems, as exemplified by D&K’s system.
The 2048 combinations in D&K’s system yield just 302 unique stress systems on overt forms of up to 7 syllables. Long words were included to avoid collapsing differences between systems that arise only in long words (Stanton 2016 finds that some patterns are distinguished by 6-syllable words and considers words of up to 7 syllables).9 This means that there is extensive global ambiguity in this system: on average, there are 7 distinct parameter specifications for each dataset.10 This ambiguity, however, is distributed quite unequally: the median number of specifications per stress system is only 2, while the range of specifications per stress system is 1 to 330. We refer to the number of specifications per stress system as its P(arameter setting)-volume, by analogy to Riggle’s (2008) R-volume, the number of constraint rankings per system. Table 1 shows the distribution of P-volumes among the stress systems in D&K’s parametric system. Each P-volume value is coupled with the number of stress systems that have this P-volume.
P-volume distribution in the stress systems defined by D&K (1990).
| P-volume | 330 | 118 | 32 | 16 | 8 | 6 | 4 | 3 | 2 | 1 |
| # systems | 2 | 2 | 8 | 16 | 4 | 16 | 42 | 8 | 116 | 88 |
As can be seen in Table 1, there are 4 stress systems with a P-volume over 32. The systems with a P-volume of 330 are word-initial and word-final stress. The next highest P-volume of 118 belongs to the systems with peninitial or penultimate stress.11 At the same time, 204 of 302 stress systems (67.5%) have a P-volume of at most 2, and 254 (84.1%) have a P-volume of at most 4. Thus, only a few stress systems are highly ambiguous as to the underlying parameter settings, while the great majority shows very limited global ambiguity. See §7.3 for information on the attestation of these systems.
P-volume provides a way to assess how the learner responds to global ambiguity. On the one hand, systems with high P-volume should be easier to find by pure chance so a learner that relies substantially on luck to find the target language may be expected to fare better on high P-volume systems on average. On the other hand, systems with high P-volume are highly globally ambiguous and often involve interdependencies between parameters that must be disentangled to settle on a complete specification for a target language. From this perspective, high P-volume languages may pose a challenge to a learning model that must incrementally commit to parameter settings, without clear or consistent evidence for crucial settings.
6.2 Simulations and results
The 302 unique stress systems described in §6.1 were presented to the learners as datafiles consisting of strings of CV, CVV, and CVC syllables with corresponding stress patterns and likelihoods of occurrence (e.g., CVV.CV.CV.CV.CV σ̀σσ́σσ 0.0003, CV.CV.CVC.CV σ̀σσ́σ 0.0003). Strings with a length of 1–7 syllables were used, and all possible combinations of the 3 syllable types of these lengths were included, yielding a total of 3 + 32 + … + 37 = 3,279 pseudowords for each stress system. During learning, a pseudoword was sampled at each iteration. Here, we assumed equal likelihood for each pseudoword.
Both the NPL and the EDPL were tested on these datasets. For the NPL, three settings for batch size were used: no pseudo-batch learning (henceforth: NPL0), pseudo-batch learning with b = 5 (henceforth: NPL5), and pseudo-batch learning with b = 10 (henceforth: NPL10). These latter values were two representative settings of the pseudo-batch size examined by Pearl (2011) (she used b = {2,5,7,10,15,20}). For the EDPL, r = 50 was used for the sample size. In total, this yields 4 learners, each of which used a learning rate of λ = 0.1.
To better evaluate these four learners, we also ran a random baseline (brute force) model as a sanity check. Checking performance against a simple baseline is standard practice in computational linguistics and important to ensure that the proposed learning mechanisms compare favourably to random search and other brute-force strategies. It provides a way to gauge whether learning models’ performance on relatively simple learning tasks have the potential to scale to the full problem of language learning.
The random baseline model encounters one data point at a time, just like the other models, but instead of gradually updating a probabilistic parameter grammar, it simply samples a random parameter specification from a uniform distribution at the first iteration and whenever a stress mismatch occurs. Since the space of categorical grammars is finite, and all the languages in D&K’s typology are categorical, this baseline model will eventually reach any target system. Because it only considers a finite space of stress systems and can flip parameters categorically, this baseline is quite strict with respect to the NPL and EDPL, which are designed to search an infinite space of probabilistic target grammars and can only update their parameter settings gradually.
Crucially, this baseline is not a serious proposal for learning stress parameters. As discussed earlier, the learning time for random search grows exponentially with the number of parameters, quickly becoming intractable as the language learning problem grows. Only learning strategies that can cope with the learning data more efficiently than random search have a chance of solving the actual language learning problem faced by children. In addition, while simulations involving variable stress are beyond the scope of the current paper, both the NPL and EDPL can in principle cope with non-determinism, while this baseline cannot. Finally, the random baseline cannot model the kind of incremental acquisition of stress seen in children, while the NPL and EDPL can. Thus, the baseline provides a benchmark for interpreting the data complexity results, but we do not consider it to be a competing model of language acquisition.
Each model was run 10 times on each of the 302 stress patterns, yielding 3020 runs per model. For the three versions of the NPL and the random baseline, each run was allowed up to 10,000,000 iterations, where an iteration is the processing of one data point in the system. Pearl (2011) estimates that children acquire a final stress pattern after about 1,666,667 data points, so this is extremely generous, but we wanted to ensure our simulations gave these models every chance to succeed. Because preliminary tests revealed fewer iterations are sufficient for convergence for the EDPL, the EDPL was given a maximum of 200,000 iterations per run.
For all learners, the simulation was stopped once the convergence criterion (at least 99% accuracy on each word in the corpus) was reached. Accuracy was assessed by sampling 100 parameter specifications from the current grammar, computing the resulting stress patterns for all words, and, for each word, counting how many specifications led to a stress match for each word; if even one word had more than 1 mismatch out of 100, there was no convergence. For globally ambiguous stress systems, this means that any grammar that leads to the desired stress assignment is accepted (see §2.1). Since assessing convergence is the most computationally intensive component of running the models, this was only done every 100 iterations (for the NPL and the random baseline, accuracy was checked even less often between 20,000 and 9,999,900 iterations: it was checked every 10,000 iterations between 20,000 and 100,000, every 100,000 iterations between 100,000 and 1,000,000, and afterwards every 1,000,000 iterations until 9,999,900 and 10,000,000).
Table 2 shows the success rates and data complexity statistics for each learner as well as the random baseline. We evaluated each of these on how many of 3020 runs reached the convergence criterion, how many of 302 stress systems converged on some run, how many stress systems converged on all runs, and how many iterations the learner required to converge (assuming it reached convergence).
Success rates and data complexity results (λ = 0.1 for all EDPL and NPL runs).
| EDPL | NPL0 | NPL5 | NPL10 | Random baseline | |
|---|---|---|---|---|---|
| # of runs that converge (% of 3020) | 2765 (91.6%) | 20 (0.7%) | 143 (4.7%) | 143 (4.7%) | 3020 (100%) |
| # of stress systems that converge on ≥1 run (% of 3020) | 281 (93.0%) | 2 (0.7%) | 28 (9.3%) | 24 (7.9%) | 302 (100%) |
| # of stress systems that converge on all 10 runs (% of 320) | 269 (89.1%) | 2 (0.7%) | 8 (2.6%) | 9 (3.0%) | 302 (100%) |
| Median (maximum) # of iterations/data points till convergence | 200 (66,200) | 200,000 (700,000) | 6,300 (9,999,900) | 3,400 (9,999,900) | 800 (30,000) |
As can be seen in Table 2, the EDPL performs well both in terms of its success rates and its data complexity. It learns 93% of the systems in the typology at least some of the time, while 89.1% of the systems are learned on all runs. The random baseline learns all 302 stress systems, but not all of these are attested (§7.3). See §7.3 for an analysis of which (attested) systems were learned by the EDPL and NPL. Moreover, the 91.6% of runs that reach the convergence criterion do so quickly: the median number of iterations needed to find the solution is just 200 iterations. These data complexity numbers are well below Pearl’s (2011) estimated 1,666,667 data forms a human child requires, and they improve over the random baseline, which requires a median of 800 iterations (the maxima for the random baseline and the EDPL are in the same general range, as well).12 Thus, on all metrics, the EDPL meets the goals we outlined for the learning models.
The NPL, on the other hand, fares poorly: it is unable to learn the typology, and if it does converge, it does so considerably slower than guessing at random. NPL0 learns less than 1% of the typology, and for the successful 0.7% of runs, the median number of data points required is much higher than for the random baseline (200,000 vs. 800). The NPL with pseudo-batch learning fares slightly better, but still fails to learn more than 90% of stress systems, and the median number of iterations is still considerably greater than for the random baseline on the small proportion of runs that are successful. This level of performance falls short of the goals we set out for the learning models and below a minimal standard required for successful language learning.
6.3 Interim Discussion
The simulation results reveal a marked difference between the NPL and the EDPL. While the EDPL learns almost all stress systems and does so faster than random guessing, the NPL learns only a few stress systems, and does so slower than random guessing. We conclude that the NPL is not a viable model of stress parameter learning, at least not for complex stress systems with the sorts of ambiguities that are present in D&K’s typology.
Beyond establishing extensive quantitative evaluations for both learning models, these results also undermine the argument for domain-specific mechanisms. Pearl’s (2011) comparison between domain-general and domain-specific learning mechanisms relied on a domain-general learning model (the NPL) that cannot cope with the sorts of ambiguities typical to stress parameter systems. The present results show that the NPL’s failure to learn English stress should not be taken as evidence against domain-general learning generally: we demonstrate that there exist domain-general learning strategies that are much more effective than the NPL.
The encouraging results of the EDPL on D&K’s full typology show that the domain-specific learning mechanisms D&K posit for their parametric system are likely unnecessary. The EDPL, a domain-general learner, succeeds in efficiently learning 93% of stress systems in this typology without the use of cues, parameter ordering, or defaults. As mentioned earlier, Gillis et al. report a 80% success rate on a similar experiment with D&K’s domain-specific learner, which does not surpass the EDPL’s performance. To better understand how to interpret our quantitative results, we present in §7 an in-depth analysis of the NPL’s and EDPL’s learning outcomes.
7 General discussion: analysis of learning outcomes
7.1 Global ambiguity and the NPL
The few stress systems that NPL learns successfully tend to be those with very high global ambiguity. As shown in Table 3, all variants of the NPL show a high positive Somers’ D rank correlation between successful convergence on a run and the P-volume (§6) of the target stress system on that run.13 Indeed, NPL0 even has a perfect rank correlation. As discussed in §4.4, the NPL’s learning process involves a great deal of random and disruptive noise. Occasionally, the random noise lands the learner close to the target system, which is more likely to occur for systems with high P-volume, since there are more distinct parameter specifications that correspond to the target system. Thus, this correlation indicates NPL’s successes are strongly driven by random chance.
Somers’ D rank correlation: successful convergence dependent on P-volume.
| EDPL | NPL0 | NPL5 | NPL10 | |
|---|---|---|---|---|
| Somers’ D | .03 | 1 | .75 | .77 |
In contrast, the EDPL’s successes shows virtually no correlation with P-volume. This confirms that the EDPL is not driven by random chance. The only randomness to its updates comes from the sampling used to estimate the Reward value and the random order in which data are presented to the learner. Since the EDPL offers a principled solution to the Credit Problem, global ambiguity does not necessarily make learning easier. It can be helpful in cases where high P-volume corresponds to a stress system with many mutually compatible analyses and few crucial parameter settings. However, as discussed in §2.1, high P-volume can also correspond to cases where there are many mutually incompatible analyses, and a learner sensitive to the Credit Problem must disentangle this confusing evidence. The next section takes a closer look at how this affects learning for the EDPL.
7.2 Local ambiguity and the EDPL
For the EDPL, learning success depends on the extent to which learning data unambiguously supports crucial parameter settings. See Hucklebridge (2020) for an in-depth analysis of how ambiguity about crucial parameter settings affects EDPL’s learning curves in the syntactic domain. The most challenging stress systems are those that crucially require foot structure for which there is only highly ambiguous evidence. To illustrate this, in (13) we have classified the stress systems in the typology into four types based on the degree of unambiguous evidence for hidden structure. Using this classification, we show that the challenging cases for the EDPL are those where hidden structure is signalled by very little information in the data. The EDPL’s performance on each class is shown in Table 4. The NPL’s performance on these classes is shown for reference only.
Success on learning stress systems split up by secondary stress and foot shape.
| Type A | Type B | Type C | Type D | |
|---|---|---|---|---|
| Number of stress systems (runs) | 196 (1960) | 40 (400) | 36 (360) | 30 (300) |
| EDPL successful runs (%) | 1932 (98.6%) | 400 (100%) | 320 (88.9%) | 113 (37.7%) |
| NPL0 successful runs (%) | 0 (0%) | 20 (5.0%) | 0 (0%) | 0 (0%) |
| NPL5 successful runs (%) | 0 (0%) | 112 (28.0%) | 25 (6.9%) | 6 (2.0%) |
| NPL10 successful runs (%) | 0 (0%) | 123 (30.8%) | 24 (6.7%) | 0 (0%) |
| (13) | 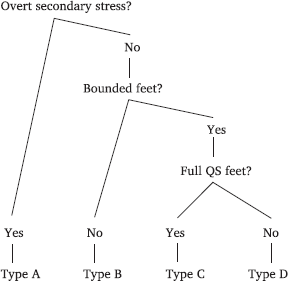 |
As indicated in (13), Type A stress systems are those with overt secondary stress. Type B stress systems have no overt secondary stress and are compatible with unbounded feet. Type B includes systems with fixed initial, peninitial, penultimate, and final stress.14 Type C and D stress systems also lack overt secondary stress, but require bounded feet to be constructed throughout the word. The difference between types C and D lies in the type of bounded foot that is required: Type C stress systems can be accounted for with “full” (i.e., non-degenerate) quantity-sensitive feet, e.g., stress the rightmost L-to-R non-degenerate QS trochaic foot: ka(laːda)(máta)na, while Type D stress systems require either quantity-insensitive feet, e.g., stress the rightmost L-to-R QI trochaic foot (kalaː)(dama)(tána) or degenerate feet, e.g., stress the rightmost L-to-R QS potentially degenerate trochaic foot: (ka)(laːda)(mata)(ná).
Overt secondary stress (Type A) guarantees that the head of each foot is expressed as a stress mark, which means that the number of feet and the approximate location of foot boundaries (always adjacent to a stressed syllable) can be read off the overt form. This gives Type A stress systems a relatively unambiguous relationship between overt form and foot structure.
The absence of overt secondary stress in the data (Types B/C/D) introduces additional ambiguity: there could be multiple feet even though there is just one stress. However, for unbounded feet (Type B), the division of the word into feet is still signalled by the segmental makeup of the word: foot boundaries are either at the word boundary (modulo extrametricality) or just before/after a heavy syllable: consider (ka)(láːdamatana)<bi> for Foot=Trochee and (kalaː)(damataná)<bi> for Foot=Iamb. This means that, once the learner has seen sufficient evidence for unbounded feet (for instance, main stress on the 4th syllable of a 7-syllable word), there are only a handful of different foot structures available for a given word.
Type C and D lack secondary stress and require bounded feet: they require multiple feet in (longer) words, but only the head foot gets stress. Such systems have one stress mark that fluctuates between one or two positions in the word (e.g., penult vs. final): this minimal information is the only evidence of the existence and details of an iterative bounded footing system, e.g., if stress falls on the rightmost L-to-R QI non-degenerate trochee, its location varies between the penultimate and antepenultimate syllable depending on the length of the word: (kala)(máta), (kala)(máta)na.
Among the patterns with bounded feet, the Type C systems, which can be represented with full QS feet, provide the most information to finding silent bounded feet: heavy syllables provide landmarks for the location of feet, while a restriction to full (non-degenerate) feet severely limits the possible locations of feet relative to stress position: initial stress on a light syllable only works with trochees – and final stress on a light syllable only works with iambs – if degenerate feet are prohibited. For instance, this is the case in Creek (Hayes 1995; D&K:177–8), where stress falls on the rightmost L-to-R (QS non-degenerate) iamb: (apa)(taká) ‘pancake’. Stress always falls an even number of syllables from the rightmost heavy syllable: (taːs)(hokí)ta ‘to jump (dual subj.)’; and there is never stress on a light initial syllable or light syllable following a heavy syllable because this would require a word-initial degenerate iamb: *(í)fa instead of (ifá) ‘dog’, *(ic)(kí) instead of (íc)ki ‘mother’.
The remaining stress systems (Type D) provide the greatest hidden structure challenge. These systems lack secondary stress, but require bounded feet that are either quantity-insensitive or (optionally) degenerate. In a quantity-insensitive system, the only landmarks for the location of bounded feet are the word edges and the location of main stress, meaning that the foot boundaries between unstressed syllables are not overtly cued – consider the case where stress falls on the rightmost L-to-R QI non-degenerate iamb: (kala)(maːta)(nabí); in this case, the boundary la)(maː is only signalled by the location of primary stress on [bi], while foot boundaries are also signalled by heavy syllables in Type C Creek. If degenerate feet are necessary to account for the stress pattern, evidence for foot headedness can be unclear: for instance, there might be initial stress in a crucially iambic system – consider the case where stress falls on the leftmost R-to-L potentially degenerate iamb: (ká)(lama)(tana). Compare this to Type C Creek, where there can be final but not initial stress, which cues iambs. As discussed in §7.3, Type D systems are unattested except for fixed antepenultimate stress (where stress falls on the rightmost L-to-R QI trochee with right extrametricality and silent secondary stress).
Table 4 shows that successful convergence of the EDPL follows this difficulty gradient: Type A and B stress systems are learned in practically all cases,15 Type C systems are learned approximately 90% of the time (the 10% non-convergence is due to 2 specific stress systems discussed in §7.3), and Type D systems, approximately 40% of the time. This distribution of success rates confirms that the EDPL only has trouble learning stress systems when little evidence for the necessary foot structure exists. All systems have hidden foot structure, but it is only when the data are highly ambiguous about which analysis (setting of parameters) is right that the EDPL has trouble learning the target settings.
A further significant division in terms of ambiguity among Type C/D stress systems is whether they ever assign stress more than 1 syllable away from the word edge. Let “1-in” stress systems be those that have stress at most 1 syllable from the edge (initial, peninitial, penultimate, or final) and “2-in” stress systems be those that can have stress 2 syllables from the edge (post-peninitial or antepenultimate). Examples: Type C 1-in: stress rightmost L-to-R QS non-degenerate iamb, no extrametricality: (kala)(matá)na, (kala)(matá), (kaː)(lamá)ta; Type C 2-in: like Type C 1-in, but with right extrametricality: (kala)(matá)<na>, (kalá)ma<ta>, (kaː)(lamá)<ta>; Type D 1-in: stress rightmost L-to-R QI potentially degenerate trochee, no extrametricality: (kala)(mata)(ná), (kala)(máta); Type D 2-in: like Type D 1-in, but with right extrametricality: (kala)(matá)<na>, (kalá)ma<ta>.
In “1-in” stress systems, none of the individual data points require bounded feet, while the stress system as a whole does: final/initial stress and penult/peninitial stress are all consistent with unbounded feet (see (2,3) in §2.1). Bounded feet are only strictly necessary to represent post-penititial or antepenultimate stress data points: <σ>(σσ́)… or …(σ́σ)<σ>. This gives “2-in” stress systems an advantage: they feature data points with unambiguous evidence for bounded feet.
As shown in Table 5, the “2-in” vs. “1-in” division corresponds to marked differences in the EDPL’s performance. “2-in” Type C systems provide evidence for bounded feet and provide relatively unambiguous cues to foot location/shape (full QS feet): these show perfect learning by the EDPL. The EDPL is still successful over 70% of the time on systems that include just one of these sources of ambiguity: the “1-in” Type C systems and “2-in” Type D systems. “1-in” Type D systems have maximal ambiguity: there is no secondary stress, and bounded feet are necessary, but none of the overt forms provide incontrovertible evidence for bounded feet, and there are no clear cues to foot location or shape. The EDPL’s performance is poor only for these systems where many different sources of ambiguity coincide.
Success on learning Type C/D systems split by stress-to-word edge distance.
| Type C | Type D | ||||
|---|---|---|---|---|---|
| 2-in | 1-in | 2-in | 1-in | ||
| Number of stress systems (runs) | 20 (200) | 16 (160) | 14 (140) | 16 (160) | |
| EDPL successful runs (%) | 200 (100%) | 120 (75.0%) | 100 (71.4%) | 13 (8.1%) | |
| NPL0 successful runs (%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | |
| NPL5 successful runs (%) | 1 (0.5%) | 24 (15.0%) | 0 (0%) | 6 (3.8%) | |
| NPL10 successful runs (%) | 15 (7.5%) | 9 (5.6%) | 0 (0%) | 0 (0%) | |
Our analysis indicates that, in general, learning data that provide highly ambiguous or contradictory support for settings of crucial parameters are particularly difficult for the EDPL. It is not the presence of hidden structure per se that creates challenges for the learner; rather, challenges arise when hidden structure creates ambiguity about crucial parameter settings. Sensitivity to this sort of ambiguity is therefore a general prediction of the EDPL that extends beyond D&K’s framework. However, the relative learning difficulty of each stress system also depends on the grammatical framework assumed, which determines what analytical options are available to the learner. This connection between theory and learning has potential to provide novel predictions to differentiate linguistic theories. We return to this topic in the conclusion.
7.3 Relationship between EDPL’s success rates and attestedness
A rich body of experimental and computational work supports the hypothesis that soft biases outside of the grammatical system play an important role in shaping linguistic typology (see Culbertson 2012; Moreton & Pater 2012a; b; Jarosz 2019 for overviews). Recent computational work has supported one possible source of such a bias: learning biases inherent to statistical learning. This line of research shows that when statistical learning models are applied to computational implementations of linguistic theories, learning outcomes often mirror typological skews (Pater 2012; Jarosz 2016; Stanton 2016; Staubs 2016; O’Hara 2017; Breteler 2018; Hughto 2018; Prickett 2019; Hucklebridge 2020). From this perspective, linguistic theory provides more options and representations than are fully realized in typology. Some combinations of options, while in principle available to learners, may be un- or under-represented because they pose particularly difficult learning challenges. If this is the case, the linguistic framework is expected to overgenerate, with some unattested languages allowed by UG being particularly challenging from a learning perspective. In this section, we present the results of a preliminary typological survey examining the correspondence between the attestation of languages in D&K’s framework and their learning outcomes for the EDPL.
While we believe these results are encouraging, we wish to emphasize several limitations of these findings. First, as discussed above, the relative learning difficulty of each stress system depends crucially on the D&K framework. Second, the simulations here make the simplifying assumption that all syllable type sequences are equally frequent in the input: learning outcomes could change with different input statistics. Third, classifying stress systems as attested or not is not entirely trivial. Our analysis relies on a manual search of StressTyp2 (Goedemans et al. 2015), a large-scale typological database of stress systems, for patterns that match the predictions of the theory. We find that 48 of D&K’s predicted stress systems correspond to at least one language in the database – in the following discussion, we refer to these patterns as attested. Of course, it is important to keep in mind that the database may be missing some attested languages.
Table 6 presents results by Types (§7.2). Nearly all the attested stress systems fall into the A, B, and C Types from Table 4. Only one system of Type D is attested: fixed antepenultimate stress (which requires bounded QI feet without overt secondary stress). This system is consistently learned by the EDPL on all runs. Thus, while the EDPL’s lowest performance is on stress systems of Type D, none of these problematic cases are attested in StressTyp2.
Attested stress systems broken down by Type.
| Type A | Type B | Type C | Type D | |
|---|---|---|---|---|
| Attested languages | 23 | 16 | 8 | 1 |
| Convergent runs | 228/230 (99.1%) | 160/160 (100%) | 60/80 (75%) | 10/10 (100%) |
In fact, there are just two attested stress systems that are consistently not learned by the EDPL.16 These are Type C systems in which CVC syllables are light. One system stresses the rightmost R-to-L QS non-degenerate trochee: ( L), (ĹL), (H)(
L), (ĹL), (H)( ), L(
), L( ) (French (phrasal-level stress): Martinet 1969; Selkirk 1978; Hayes 1995;17 Sorbian: Bethin 1998; in both cases, only schwa counts as short), and the other is its exact mirror image: (L
) (French (phrasal-level stress): Martinet 1969; Selkirk 1978; Hayes 1995;17 Sorbian: Bethin 1998; in both cases, only schwa counts as short), and the other is its exact mirror image: (L ), (LĹ), (
), (LĹ), ( )(H), (
)(H), ( )L (Iron Ossetic, Abaev 1964; Borise & Erschler 2020; phrasal-level stress, only reduced vowels count as short). Interestingly, the two stress systems identical to these except that CVCs are treated as heavy are consistently learned by the EDPL. This is because when CVCs are heavy, two thirds of the syllables in the learning data have potential to cue quantity sensitivity, while when CVCs are light, only one third of the syllables, those with long vowels, have that opportunity. This suggests that the EDPL’s learning outcomes can depend on the prevalence of heavy syllables in the learning data.18 Recent results by Zuiderwijk (2020) do indeed confirm this: if the proportion of CVV syllables is increased to two-thirds of the dataset, these two stress systems are consistently learned. It is a question for further work what the EDPL predicts for learning based on the actual statistical distribution of segmental and stress patterns in these languages.
)L (Iron Ossetic, Abaev 1964; Borise & Erschler 2020; phrasal-level stress, only reduced vowels count as short). Interestingly, the two stress systems identical to these except that CVCs are treated as heavy are consistently learned by the EDPL. This is because when CVCs are heavy, two thirds of the syllables in the learning data have potential to cue quantity sensitivity, while when CVCs are light, only one third of the syllables, those with long vowels, have that opportunity. This suggests that the EDPL’s learning outcomes can depend on the prevalence of heavy syllables in the learning data.18 Recent results by Zuiderwijk (2020) do indeed confirm this: if the proportion of CVV syllables is increased to two-thirds of the dataset, these two stress systems are consistently learned. It is a question for further work what the EDPL predicts for learning based on the actual statistical distribution of segmental and stress patterns in these languages.
We tentatively conclude there is an intriguing correspondence between patterns that pose difficulty for the EDPL and patterns that appear to be unattested typologically. The two exceptions discussed above show that much further work, beyond the scope of this paper, is needed before firm conclusions about the connections between learning and typology can be made. This work will require examining how distributional properties of the data – in particular, the distribution of word lengths (Stanton 2016) and heavy syllables (Apoussidou 2007) – affect learning and how predictions for learning vary when different theoretical assumptions are made.
8 Conclusion
In this paper, we introduce a novel domain-general learning model for P&P grammars. We show how the proposed learning model provides a mathematically principled solution to the Credit Problem. The solution relies on probabilistic inference to formalise and quantify each parameter setting’s relative responsibility for each data point. We show that these learning updates can be computed efficiently and incrementally without the need for any specialized parsing mechanisms. The proposed learning algorithm, the EDPL, can be viewed as an extension of the NPL wherein the parameter-specific, continuously-valued responsibility replaces the global, binary reward value used by the NPL.
We present the first systematic tests of both the NPL and EDPL on a full stress typology, namely, the one predicted by Dresher & Kaye’s (D&K; 1990) framework. Our findings indicate that the NPL fails to cope with the ambiguity present in this typological system, learning fewer than 5% of the languages. In contrast, the EDPL learns over 90% of the languages in D&K’s framework, and over 94% of the languages in their framework that are also attested in StressTyp2. The only difference between the EDPL and the NPL is in the definition of the Reward values: the NPL does not attempt to address the Credit Problem, while the Reward values in the EDPL are mathematically defined as the share of credit attributable to each parameter setting. This minimal contrast together with the dramatic differences in performance between the NPL and EDPL support our claim that mechanisms for performing analysis on incoming data are essential for successful, domain-general learning of metrical stress.
These results have further implications for P&P frameworks of stress and phonological theory more generally. Since the EDPL is a domain-general learning model, its high performance undermines arguments made in previous work for the necessity of domain-specific learning mechanisms. We provide the first results to suggest that combining a P&P theory of universal grammar with general statistical learning mechanisms may be sufficient to account for successful learning of stress. This brings learning results for P&P closer in line with those of OT, where a number of existing domain-general learning models have been demonstrated to have similar levels of performance on metrical stress systems (Jarosz 2013a; 2015; Boersma & Pater 2016). Indeed, some of these results are for the Expectation Driven Learning model for OT (Jarosz 2015), which the EDPL is based on, making it possible for the first time to directly compare the learning predictions of OT and P&P theories of stress within the context of the same learning theory. The EDPL can also be readily applied in its current form to other P&P theories of stress (e.g., Halle & Vergnaud 1987; Hayes 1995).
Our findings have broader implications beyond P&P and beyond the domain of stress. The EDPL has already been applied outside phonology to the domain of syntax with promising results (Hucklebridge 2020; Prickett et al. 2020). Future work should further examine the EDPL in this context and compare its performance and computational properties to existing models of syntactic learning (e.g., Sakas & Fodor 2001; Yang 2002; Gould 2015). This work is also part of a broader effort to develop deeper and more explicit connections between learning and linguistic theory. In the previous section, we presented an in-depth analysis of how local ambiguity presents learning challenges for the EDPL and where learning difficulties may line up with typological attestation. While the analysis is necessarily specific to this stress system and the typological correspondence is preliminary for the reasons discussed earlier, the results are encouraging and provide support for pursuing these connections further. As Hucklebridge (2020) finds for the domain of syntax, we find that the EDPL’s learning difficulty in the stress domain depends on the quantity and quality of evidence supporting target settings of crucial parameters. Different theories make distinct representational assumptions and therefore predict learning challenges should arise in different contexts and for different patterns. Typological skews are one place where predictions of different frameworks may diverge, and we have taken the first steps toward exploring such predictions for the D&K system here.
Abbreviations
D&K – Dresher and Kaye
EM – Expectation Maximization
EDPL – Expectation Driven Parameter Learner
LRPS – Linear Reward-Penalty Scheme
NPL – Naïve Parameter Learner
OT – Optimality Theory/Theoretic
P&P – Principles and Parameters
QI – Quantity-Insensitive
QS – Quantity-Sensitive
UG – Universal Grammar
Notes
- Although the Markedness-over-Faithfulness bias (Prince & Tesar 2004) is a domain-specific addition to a domain-general strategy. [^]
- We use “trochee”/“iamb” as a shorthand for “left-headed”/“right-headed” even when feet are longer than two syllables. [^]
- D&K acknowledge that this cue would also be triggered by morphological/lexical influences on stress. Dresher (2016) underscores the importance of contrast in distinguishing these factors. Morphological/lexical factors are beyond the scope of this paper, but see Jarosz (2015) for applications of Expectation Driven Learning (the algorithm that the EDPL is based on, see §5) to lexical stress in the OT framework. [^]
- In our simulations, we disregard such built-in dependencies between parameters since they make the model more complex and do not affect which stress patterns the model generates. [^]
- The proposed order is QS – CVC – SecStress – XM/XMdir – Bounded –Main – HeavyHead – Dir/Foot. Degenerate is not included in this order because D&K consider it to be in a separate phonological module. [^]
- We present the algorithm using binary parameters here, but the algorithm can be straightforwardly extended to n-ary parameters: for a n-ary parameter there would simply be n terms in P(match|Gt). [^]
- To avoid division by zero, we added a very small number (10–250) to the number of matches for each parameter setting, which results in no update to the grammar when P(match|Gt) would otherwise evaluate to zero. [^]
- The Reward value of Main=Right equals 1 even if Main=Right yields a match just 40% of the time: because Main=Left always yields a mismatch, Main=Right is the only viable option. [^]
- We also considered including 8- and 9-syllable words, but these do not lead to any additional unique stress systems. [^]
- As an anonymous reviewer points out, this global ambiguity may be greatly reduced if foot-conditioned segmental phonological processes provide additional evidence for foot boundaries. [^]
- An anonymous reviewer points out that these high P-volumes will be drastically lower if primary stress is assigned non-metrically (van der Hulst 1996; 1997). However, the learning implications of such a model would have to be evaluated separately. [^]
- Unlike the baseline, the EDPL’s and NPL’s speed of learning depends on the learning rate. Since the EDPL outperformed the baseline with this learning rate, we did not investigate even larger learning rates, which would be expected to result in faster learning. [^]
- This was computed using SomersDelta() in the DescTools package for R (Signorell 2019). [^]
- As opposed to D&K’s (1990) original proposal, we did consider unbounded QI feet in our simulations; see footnote 4. [^]
- The EDPL needs slightly more iterations to learn Type B QS systems (median=300, maximum=800) than it does for the Type B QI systems (median=200, maximum=500). [^]
- One other system not learned by the EDPL resembles Cairene Arabic to some extent (Hayes 1995). However, the actual Cairene Arabic stress pattern cannot be modelled in the D&K framework because moraic trochees and segment extrametricality are not available. [^]
- See, e.g., Jun & Fougeron (2000); Post (2000) for non-stress analyses of prominence in French. [^]
- See Apoussidou (2007:106–107) for a similar influence of preponderance of heavy syllables on learning. [^]
Acknowledgements
We would like to thank Adam Albright, Gašper Beguš, Elan Dresher, Naomi Feldman, Edward Flemming, Isaac Gould, Bruce Hayes, Mark Johnson, Michael Kenstowicz, Andrew Lamont, Armin Mester, Erin Olson, Joe Pater, Lisa Pearl, Ezer Rasin, Juliet Stanton, Kristine Yu, Sam Zukoff, the students in LING 730 in the Fall of 2020 at UMass Amherst, and audiences at UMass Amherst, MIT, USC, Warsaw University, NECPhon 10, AMP 2017, the LSA 2017 Annual Meeting, and SCIL 2019 for their feedback that has greatly benefited this work. We would also like to thank John Iyalla Alamina for his help with technical issues. All errors remain our own.
Competing interests
The authors have no competing interests to declare.
References
Abaev, Vasilii Ivanovich. 1964. A grammatical sketch of Ossetic. Bloomington, IN: Indiana University Center in Anthropology, Folklore and Linguistics.
Apoussidou, Diana. 2007. The learnability of metrical phonology. Amsterdam: University of Amsterdam dissertation.
Archangeli, Diana & Douglas Pulleyblank. 1994. Grounded phonology. Cambridge, MA: MIT Press.
Berwick, Robert & Partha Niyogi. 1996. Learning from triggers. Linguistic Inquiry 27(4). 605–622.
Bethin, Christina. 1998. Slavic prosody: Language change and phonological theory (Cambridge Studies in Linguistics 86). Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/CBO9780511519765
Blevins, Juliette. 1995. The syllable in phonological theory. In John Goldsmith (ed.), The handbook of phonological theory, 206–244. Oxford: Basil Blackwell. DOI: http://doi.org/10.1111/b.9780631201267.1996.00008.x
Blutner, Reinhart & Henk Zeevat. 2004. Editors’ introduction: Pragmatics in Optimality Theory. In Reinhart Blutner & Henk Zeevat (eds.), Optimality Theory and pragmatics, 1–24. Houndmills, Basingstoke, Hampshire: Palgrave/Macmillan. DOI: http://doi.org/10.1057/9780230501409
Boersma, Paul. 1997. How we learn variation, optionality, and probability. IFA Proceedings 21. 43–58.
Boersma, Paul. 2003. Review of Tesar & Smolensky (2000): Learnability in Optimality Theory. Phonology 20(3). 436–446. DOI: http://doi.org/10.1017/S0952675704230111
Boersma, Paul & Bruce Hayes. 2001. Empirical tests of the Gradual Learning Algorithm. Linguistic Inquiry 32. 45–86. DOI: http://doi.org/10.1162/002438901554586
Boersma, Paul & Joe Pater. 2016. Convergence properties of a Gradual Learning Algorithm for Harmonic Grammar. In John McCarthy & Joe Pater (eds.), Harmonic Grammar and Harmonic Serialism, 389–434. London: Equinox Press.
Borise, Lena & David Erschler. 2020. Verb height indeed determines prosodic phrasing: Evidence from Iron Ossetic. Talk given at University of California Santa Cruz.
Breteler, Jeroen. 2018. A foot-based typology of tonal reassociation: Perspectives from synchrony and learnability. Amsterdam: University of Amsterdam dissertation.
Bush, Robert & Frederick Mosteller. 1951. A mathematical model for simple learning. Psychological Review 58. 313–323. DOI: http://doi.org/10.1037/h0054388
Cho, Young-mee Yu. 1999. Parameters of consonantal assimilation. München: LINCOM Europa.
Chomsky, Noam. 1981. Lectures on government and binding. Dordrecht: Foris.
Clark, Robin. 1989. On the relationship between the input data and parameter setting. Proceedings of the North Eeast Linguistic Society 19(1). 48–62.
Clark, Robin. 1992. The selection of syntactic knowledge. Language Acquisition 2(2). 83–149. DOI: http://doi.org/10.1207/s15327817la0202_1
Culbertson, Jennifer. 2012. Typological universals as reflections of biased learning: Evidence from artificial language learning. Language and Linguistics Compass 6(5). 310–329. DOI: http://doi.org/10.1002/lnc3.338
Dempster, Arthur, Nan Laird & Donald Rubin. 1977. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society. Series B (Methodological) 39(1). 1–38. DOI: http://doi.org/10.1111/j.2517-6161.1977.tb01600.x
Dresher, B. Elan. 1999. Charting the learning path: Cues to parameter setting. Linguistic Inquiry 30. 27–67. DOI: http://doi.org/10.1162/002438999553959
Dresher, B. Elan. 2016. Covert representations, contrast, and the acquisition of lexical accent. In Jeffrey Heinz, Rob Goedemans & Harry van der Hulst (eds.), Dimensions of phonological stress, 231–262. Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/9781316212745.009
Dresher, B. Elan & Jonathan Kaye. 1990. A computational learning model for metrical phonology. Cognition 34. 137–195. DOI: http://doi.org/10.1016/0010-0277(90)90042-IFodor
Fodor, Janet. 1998. Parsing to learn. Journal of Psycholinguistic Research 27(3). 339–374. DOI: http://doi.org/10.1023/A:1023255705029
Gibson, Edward & Kenneth Wexler. 1994. Triggers. Linguistic Inquiry 25(3). 407–454.
Gillis, Steven, Gert Durieux & Walter Daelemans. 1995. A Computational model of P&P: Dresher & Kaye (1990) revisited. In Frank Wijnen & Maaike Verrip (eds.), ASCLD 4: Approaches to parameter setting, 135–173. Amsterdam: Vakgroep Algemene Taalwetenschap, Universiteit van Amsterdam.
Goedemans, Rob, Jeffrey Heinz & Harry van der Hulst. 2015. StressTyp2, version 1. (http://st2.ullet.net)
Gould, Isaac. 2015. Syntactic learning from ambiguous evidence: Errors and end-states. Cambridge, MA: MIT dissertation.
Halle, Morris & Jean-Roger Vergnaud. 1987. An essay on stress. Cambridge, MA: MIT Press.
Hayes, Bruce. 1995. Metrical stress theory: Principles and case studies. Chicago, IL: The University of Chicago Press.
Heinz, Jeffrey. 2011a. Computational phonology – Part I: Foundations. Language and Linguistics Compass 5(4). 140–152. DOI: http://doi.org/10.1111/j.1749-818X.2011.00269.x
Heinz, Jeffrey. 2011b. Computational phonology – Part II: Grammars, learning, and the future. Language and Linguistics Compass 5(4). 153–168. DOI: http://doi.org/10.1111/j.1749-818X.2011.00268.x
Huang, C.-T. James & Ian Roberts. 2017. Principles and Parameters of Universal Grammar. In Ian Roberts (ed.), The Oxford Handbook of Universal Grammar. Oxford: Oxford University Press. DOI: http://doi.org/10.1093/oxfordhb/9780199573776.013.14
Hucklebridge, Shay. 2020. Learning and the typology of word order: A model of the Final-over-Final Condition. Ms., University of Massachusetts Amherst.
Hughto, Coral. 2018. Investigating the consequences of Iterated learning in phonological typology. Proceedings of the Society for Computation in Linguistics 1. 21. DOI: http://doi.org/10.7275/R5WH2N63
Jarosz, Gaja. 2006. Rich lexicons and restrictive grammars – Maximum Likelihood learning in Optimality Theory. Baltimore, MD: Johns Hopkins University dissertation.
Jarosz, Gaja. 2013a. Learning with hidden structure in Optimality Theory and Harmonic Grammar: Beyond Robust Interpretive Parsing. Phonology 30(1). 27–71. DOI: http://doi.org/10.1017/S0952675713000031
Jarosz, Gaja. 2013b. Naive parameter learning for Optimality Theory: The hidden structure problem. Proceedings of the North Eeast Linguistic Society 40(2). 1–14.
Jarosz, Gaja. 2015. Expectation driven learning of phonology. Ms., University of Massachusetts Amherst.
Jarosz, Gaja. 2016. Investigating the efficiency of parsing strategies for the Gradual Learning Algorithm. In Jeffrey Heinz, Rob Goedemans & Harry van der Hulst (eds.), Dimensions of phonological stress, 201–230. Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/9781316212745.008
Jarosz, Gaja. 2019. Computational modeling of phonological learning. Annual Review of Linguistics 5. 67–90. DOI: http://doi.org/10.1146/annurev-linguistics-011718-011832
Jun, Sun-Ah & Cécile Fougeron. 2000. A phonological model of French intonation. In Antonis Botinis (ed.), Intonation: Text, Speech, and Language Technology, 209–242. New York, NY: Springer. DOI: http://doi.org/10.1007/978-94-011-4317-2_10
Lightfoot, David. 1999. The development of language: Acquisition, change, and evolution. Oxford: Blackwell.
Martinet, André. 1969. Langue et fonction. Paris: Gonthier.
Moreton, Elliott & Joe Pater. 2012a. Structure and substance in artificial-phonology learning, Part I: Structure. Language and Linguistics Compass 6(11). 686–701. DOI: http://doi.org/10.1002/lnc3.363
Moreton, Elliott & Joe Pater. 2012b. Structure and substance in artificial-phonology learning, Part II: Substance. Language and Linguistics Compass 6(11). 702–718. DOI: http://doi.org/10.1002/lnc3.366
O’Hara, Charlie. 2017. How abstract is more abstract? Learning abstract underlying representations. Phonology 34(2). 325–345. DOI: http://doi.org/10.1017/S0952675717000161
Pater, Joe. 2010. Morpheme-specific phonology: Constraint indexation and inconsistency resolution. In Steven Parker (ed.), Phonological argumentation: Essays on evidence and motivation, 123–154. London: Equinox.
Pater, Joe. 2012. Emergent systemic simplicity (and complexity). McGill Working Papers in Linguistics 22(1).
Pearl, Lisa. 2007. Necessary bias in natural language learning. College Park, MD: University of Maryland dissertation.
Pearl, Lisa. 2011. When unbiased probabilistic learning is not enough: Acquiring a parametric system of metrical phonology. Language Acquisition 18(2). 87–120. DOI: http://doi.org/10.1080/10489223.2011.554261
Pearl, Lisa & Jeffrey Lidz. 2009. When domain-general learning fails and when it succeeds: Identifying the contribution of domain specificity. Language Learning and Development 5(4). 235–265. DOI: http://doi.org/10.1080/15475440902979907
Post, Brechtje. 2000. Tonal and phrasal structures in French intonation. Nijmegen: Catholic University Nijmegen dissertation.
Prickett, Brandon. 2019. Learning biases in opaque interactions. Phonology 36(4). 627–653. DOI: http://doi.org/10.1017/S0952675719000320
Prickett, Brandon, Kaden Holladay, Shay Hucklebridge, Max Nelson, Rajesh Bhatt, Gaja Jarosz, Kyle Johnson, Aleksei Nazarov & Joe Pater. 2020. Learning syntactic parameters without triggers by assigning credit and blame. Chicago Linguistic Society 55.
Prince, Alan & Bruce Tesar. 2004. Learning phonotactic distributions. In René Kager, Joe Pater & Wim Zonneveld (eds.), Constraints in phonological acquisition, 245–291. Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/CBO9780511486418.009
Prince, Alan & Paul Smolensky. 1993/2004. Optimality Theory: Constraint interaction in generative grammar. Malden, MA: Blackwell. DOI: http://doi.org/10.1002/9780470759400
Riggle, Jason. 2008. Counting rankings. Columbus, OH: Tenth Meeting of the ACL Special Interest Group on Computational Morphology and Phonology. DOI: http://doi.org/10.3115/1626324.1626329
Rodríguez-Mondoñedo, Miguel. 2008. The acquisition of Differential Object Marking in Spanish. Probus 20(1). 111–145. DOI: http://doi.org/10.1515/PROBUS.2008.004
Sakas, William. 2016. Computational approaches to learning parameter settings. In Jeffrey Lidz, William Snyder & Joe Pater (eds.), Oxford Handbook of Developmental Linguistics, 696–724. Oxford: Oxford University Press. DOI: http://doi.org/10.1093/oxfordhb/9780199601264.001.0001
Sakas, William & Janet Fodor. 2001. The structural triggers learner. In Stefano Bertolo (ed.), Language Acquisition and Learnability, 172–233. Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/CBO9780511554360.006
Selkirk, Elizabeth. 1978. The French foot: On the status of mute e. Studies in French Linguistics 1(2). 141–150.
Signorell, Andri. 2019. Package “DescTools”. (https://cran.r-project.org/web/packages/DescTools/DescTools.pdf).
Stanton, Juliet. 2016. Learnability shapes typology: The case of the midpoint pathology. Language 92(4). 753–791. DOI: http://doi.org/10.1353/lan.2016.0071
Staubs, Robert D. 2016. Computational modeling of learning biases in stress typology. Amherst, MA: University of Massachusetts dissertation.
Straus, Kenneth. 2008. Validations of a probabilistic model of language learning. Boston, MA: Northeastern University dissertation.
Tesar, Bruce. 1995. Computational Optimality Theory. Boulder, CO: University of Colorado Boulder dissertation.
Tesar, Bruce. 2013. Output-Driven Phonology. Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/CBO9780511740039
Tesar, Bruce & Paul Smolensky. 1998. Learnability in Optimality Theory. Linguistic Inquiry 29(2). 229–268. DOI: http://doi.org/10.1162/002438998553734
Tesar, Bruce & Paul Smolensky. 2000. Learnability in Optimality Theory. Cambridge, MA: MIT Press. DOI: http://doi.org/10.7551/mitpress/4159.001.0001
van der Hulst, Harry. 1996. Separating primary accent and secondary accent. In Rob Goedemans, Harry van der Hulst & Ellis Visch (eds.), Stress patterns of the world, 1–26. The Hague: Holland Academic Graphics.
van der Hulst, Harry. 1997. Primary accent is non-metrical. Rivista di Linguistica 9. 99–127.
Van Oostendorp, Marc. 2015. Parameters in phonological analysis: Stress. In Antonio Fabregas, Jaume Mateu & Michael Putnam (eds.), Contemporary Linguistic Parameters, 234–258. Contemporary Studies in Linguistics. London: Bloomsbury.
Yang, Charles. 2002. Knowledge and learning in natural language. Oxford: Oxford University Press.
Zuiderwijk, Jos. 2020. De invloed van de frequentie van zware lettergrepen op de leerbaarheid in domeinalgemene leerders van bepaalde kwantiteitssensitieve klemtoonsystemen [The influence of heavy syllables’ frequency on learnability in domain-general learners of certain quantity sensitive stress systems]. Utrecht: Utrecht University BSc thesis.

