1. Introduction
The universal quantifier phrase headed by every can be modified by various scalar modifiers:
- (1)
- a.
- b.
- c.
- Almost everybody was there.
- Absolutely everybody was there.
- Nowhere near everybody was there.
Other expressions that fall in the same class as almost include: just about, nearly practically, essentially, virtually, close to, damn near, pretty much, somewhere around. Other negative modifiers include: not nearly, far from, not quite, and nothing like. I will not investigate these other expressions here.
Such expressions can be used with other kinds of quantifier phrases as well:
- (2)
- a.
- b.
- c.
- Almost all the students were there.
- Absolutely all the students were there.
- Nowhere near all the students were there.
- (3)
- a.
- b.
- c.
- Almost no students were there.
- Absolutely no students were there.
- ?Nowhere near no students were there.
In this paper, I present a compositional semantics for such scalar modifiers, on analogy with the cross-categorial semantics of negation presented in Collins and Postal 2014.
Section 2 presents the framework for the syntax and semantics of negation in Collins and Postal 2014 and the basic proposal for scalar modifiers. Section 3 shows how generalized quantifiers can be arranged on scales (positive and negative). Section 4 discusses scalar modification of negative quantifier phrases. Section 5 discusses the complex scalar modifier nowhere near. Section 6 presents a summary of a survey of acceptability judgments on various complex scalar modifiers. Section 7 discusses absolutely. Section 8 discusses the distribution of negative polarity items in modified quantifier phrases. Section 9 explains why scalar modifiers cannot modify existential quantifier phrases. Section 10 is the conclusion.
2. Proposal
I follow Collins and Postal 2014 in adopting the following semantic value of negation:
- (4)
- If X has a semantic type ending in <…, t>, then
- NEG takes X with semantic value: λP1….λPn […]
- And returns Y with semantic value: λP1…λPn ¬[…]
For propositional variables p (no predicate abstraction), the negation is simply ¬p. On this view, negation can combine with constituents of various different types, parallel to the analysis of conjunction given in Partee and Rooth (1983). One way to think of it is that the function negation denotes depends on the type of its argument (where the different types partition the domain of the negation function).
Consider the following example:
- (5)
- Not everybody was there.
Collins and Postal 2014 assume that in (5), not everybody is a constituent, and that negation modifies the DP everybody, in other words, the structure is [NEG [DP everybody]] (see also Collins 2016). There is clear evidence for Collins and Postal’s constituent structure assumption. [not every N] phrases trigger Negative Inversion:
- (6)
- Not every day do you hit three home runs in a postseason elimination game at Dodger Stadium.
- (https://www.latimes.com/sports/dodgers/story/2021-10-21/chris-taylor-three-home-runs-dodgers-win-braves-nlcs-game-5-mlb)
Following Haegeman 2012 and Collins and Postal 2014 Negative Inversion involves a negative phrase in Spec FocP. But if [not every day] occupies Spec FocP, then it is a constituent.
In the framework of (4), negation in (5) has the following semantic value in (7):
- (7)
- ⟦NEG⟧ = λQ.λP.¬[Q(P)]
In other words, NEG takes a generalized quantifier argument of type <<e,t>,t> and yields a generalized quantifier of type <<e,t>,t>.
On analogy with the proposals about the syntax and semantics of negation in Collins and Postal 2014, I propose that almost can modify a quantifier phrase with the structure [almost DP], and has the following semantic value (when it modifies a quantifier phrase):
- (8)
- ⟦almost⟧ = λQ.λP.∃X[near(X,Q) ∧ X(P)]
In both cases, not everybody and almost everybody involve modification of the DP everybody. Just as in the case of negation, almost takes a generalized quantifier of type <<e,t>,t> and yields a generalize quantifier of type <<e,t>,t>. To illustrate, here is the compositional analysis of almost everybody:
- (9)
- a.
- ⟦almost⟧ (⟦everybody⟧) =
- b.
- λQ.λP.∃X[near(X,Q) ∧ X(P)] (λR.∀x[person(x)
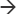 R(x)]) =
R(x)]) =
- c.
- λP.∃X[near(X, λR.∀x[person(x)
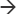 R(x)]) ∧ X(P)]
R(x)]) ∧ X(P)]
As (9c) shows, ⟦almost everybody⟧ takes an argument of type <e,t> (a predicate) and yields a truth value (of type <t>), and so ⟦almost everybody⟧ is a generalized quantifier of type <<e,t>, t>.
An analysis closely related to the one given in (8), also in the spirit of Collins and Postal 2014, is the following. Suppose that instead of the relation near in (8) we used a meta-language function distance which takes two quantifiers X and Q and yields the distance between them as a percentage. Then suppose that the maximum distance between two quantifiers consistent with almost was n (perhaps 5%). In other words, almost everybody would be 95% (of the cardinality of the restriction). Then the semantic value of almost could be stated as follows (on the notation iX see Heim and Kratzer 1998: 85):
- (10)
- ⟦almost⟧ = λQ.ιX[X < Q ∧ distance(X,Q) = n]
According to this definition, almost takes a generalized quantifier Q of type <<e,t>,t> and returns a generalized quantifier X of type <<e,t>,t> that is less than Q and at a distance of n from Q on the contextual scale. I have no data distinguishing (8) from (10), and I will adopt (8) for the rest of the paper.
In the next section I will discuss scales of generalized quantifiers and the definition of near in (8).
3. Scales
Following (Horn 1972: 75; 2001: 235), I assume that all monotonic generalized quantifiers are organized into two related scales, one for increasing quantifiers (the positive scale) and one for decreasing quantifiers (the negative scale):
- (11)
- a.
- b.
- some
- not every
- <
- <
- half
- less than half
- <
- <
- every
- no
- (positive)
- (negative)
All generalized quantifiers on a scale have the same NP restriction. In other words, each restriction (the denotation of NP) gives rise to two scales: a negative scale and a positive scale. The positive scale is defined by the smallest number of elements (satisfying the restriction) in each member set of a generalized quantifier. For example, for the DP [some boy], each member set of the generalized quantifier has one or more boys in it. The negative scale is defined by the greatest number of elements in each member set of the generalized quantifier.
The scales in (11) are model theoretic objects (each defined as a total ordering of generalized quantifiers), not conventionalized scales of lexical items (contra Horn 1972). There may be points on the scale that are lexicalized (e.g., every, no, some), but other points that are not lexicalized (e.g., not every). A particular generalized quantifier (of type <<e,t>,t>) with a particular restriction (a set of elements in the domain) will by its definition be part of either the negative or the positive generalized quantifier scale for that restriction. Below, I argue that it is possible to quantify over the generalized quantifiers which are members of scales defined in this sense.
For example, consider a quantifier phrase like every boy which denotes a set of sets (each containing every boy), where the cardinality of the set of boys is n (an integer greater than or equal to zero). The generalized quantifier denoted by every boy is the right endpoint of the positive scale in (11a).
From the standpoint of the scales in (11), negation and scalar modifiers have complementary functions. The function of negation is to move from one scale to another (e.g., when every boy on the positive scale is negated it becomes not every boy on the negative scale), and the function of the scalar modifiers is to move along a single scale.
In (8), near is a relation in the meta-language that evaluates the nearness of one generalized quantifier to another along a scale of generalized quantifiers (on the use of scales in the semantics of almost, see Hitzeman 1992). The appropriate generalized quantifier scale is contextually determined by the restriction of Q and whether Q is positive or negative. In (8) it would be more accurate to write nearS, where S is the contextually appropriate scale (with similar changes to (10)). But I leave out the scale subscript for brevity’s sake.
What counts as near depends on contextual factors (e.g., the goals and beliefs of the speaker and hearer). For example, suppose we have a party, and invite 100 people. If 95 of the people show up, we might be happy saying (12):
- (12)
- Almost everybody showed up.
(12) has the following truth conditions:
- (13)
- ƎX[near(X, ⟦everybody⟧) ∧ X(⟦showed up⟧)]
Translating into English: There is a generalized quantifier X that is near to ⟦everybody⟧ on the positive generalized quantifier scale such that X applied to ⟦showed up⟧ is true.
In this case, the generalized quantifier X can be taken as 95% of the people, so that (13) entails (14):
- (14)
- 95% of the people showed up.
A property of the analysis in (13) is that (15a) does not entail (15b).
- (15)
- a.
- b.
- c.
- Almost everybody was there.
- Not everybody was there.
- Everybody was there.
The reason why (15b) is not an entailment of (15a) is that (15a) and (15c) can be true at the same time (see (16) and (17) below for supporting evidence). Adding a negative entailment to the semantics of almost would be easy to do: λQ.λP.ƎX[near(X,Q) ∧ X(P) ∧ ¬Q(P)] (on such an analysis, see Crnič 2018: 743). But based on the examples in (16) and (17) below, I argue that no such addition is possible.
Rather, I claim that (15b) is a scalar conversational implicature of (15a) (see Sadock 1981). Since (15b) is a scalar conversational implicature of (15a), it can be cancelled in the right contexts. I do not take any position in this paper on how scalar implicatures are formally calculated (see Chierchia, Fox, Spector 2012 for discussion, and Spector 2014 for an analysis of almost involving an exhaustivity operator).
To show that almost does not give rise to a negative entailment (when modifying quantifier phrases), consider (16) (see Horn 2011:14 for non-quantifier uses of almost where the negative implication is cancellable, and Hitzeman 1992: 233 for discussion):
- (16)
- a.
- b.
- c.
- d.
- e.
- As long as you finish nearly/almost all of your vegetables, you can watch TV.
- Just about/almost everybody should be present, before we can vote.
- We should start as soon as almost everybody is here; in fact, everybody is here, so let’s start.
- Not only did almost everybody show up, (in fact) everybody did.
- If you want to pass the exam, you have to answer almost all questions correctly.
In (16a), if the child finishes eating all of the vegetables, they will not be stopped from watching TV. In (16b), if everybody is present, the vote will not thereby become invalid. (16c) and (16d) were suggested to me by Jack Hoeksema and Larry Horn respectively. (16e) is from Nouwen (2006: 165), who notes that (16e) “allows for exams being passed where all questions were answered correctly.” He ends up concluding: “…I offer the weak conclusion that the polar component of almost is not part of conventional meaning.”
Similarly, there is a clear difference between the following two sentences (personal communication, Paul Postal):
- (17)
- a.
- b.
- Almost everybody showed up. In fact, everybody did.
- Not quite everybody showed up. *In fact, everybody did.
In context, (17a) is acceptable (e.g., “Let’s start the meeting….”). But in any context, (17b) is a contradiction (indicated by the * before the second clause). The scalar modifier not quite clearly does have a negative entailment, and it cannot be cancelled (see Nouwen 2008 for more on the difference between almost and not quite). If almost had a negative entailment or presupposition, it is not clear how the contrast in (17) would be captured.
The sentences in (16) all involve almost modifying a quantifier phrase. Part of the debate about the negative implication of almost in the literature (see Horn 2011) may have to do with the fact that with other categories, the negative implication is not always cancellable. For example, the sentence [John almost died] seems false if in fact John died (for similar examples, see Penka 2011: 237, Jayez and Tovena 2008:14). I have nothing to contribute to this issue here, since my paper focuses uniquely on modification of quantifier phrases, where the facts in (16) and (17) show that the negative implication is cancellable in the right context (suggesting that there is no negative entailment or negative presupposition, although there definitely is a scalar conversational implicature).
Penka (2011: 237) proposes a treatment where: “…almost applied to a proposition p is true iff p is false in the actual world but an alternative proposition q close to p on the corresponding scale is true.” However, she assumes that syntactically at LF almost occupies a clause initial position and “…there is thus a discrepancy between the surface position of almost and the position where it is interpreted.” (pg. 243). See also Penka 2005, 2006.
My account has no such syntax/semantics discrepancy. The scalar modifiers are sisters of DP and compose semantically with their sisters. This is achieved by giving almost a semantic value that maps generalized quantifiers to generalized quantifiers, in the same way that negation maps generalized quantifier to generalized quantifiers in the framework of Collins and Postal 2014. My analysis avoids undesirable theoretical consequences of Penka’s approach. For example, Penka notes (pg. 244), “…for QR of a sentential operator to have any effect at all, its trace cannot be interpreted. That means that we would have to stipulate an unusual kind of movement that does not leave a trace.” My analysis does not suffer from any such issues.
4. The Negative Scale
Scalar modifiers also modify negative quantifier phrases (see Zanuttini 1991: 116–117 for a similar fact about n-words in Italian):
- (18)
- Almost nobody showed up.
(18) will have the following truth conditions:
- (19)
- ƎX[near(X, ⟦nobody⟧) ∧ X(⟦showed up⟧)]
Only quantifiers X near the right edge of the scale in (11b) will count as near to nobody. In the context of a party where 100 people were invited, depending on contextual factors, X might be defined as 5% of the people.
Now consider (20):
- (20)
- Almost half of the people were there.
This means a little less than half of the people were there, not that a little more than half of the people were there. So, the following condition on the meta-language relation near holds (for discussion of this property see Penka 2006 and Nouwen 2006):
- (21)
- near(X,Q) only if X is less than Q (on the contextual scale S)
A reviewer makes the interesting proposal that in the case of almost (21) could be related to the morphological form of almost, which seems to be based on most (not least). In other words, because of the presence of most in almost, (20) would entail ‘At most half of the people were there.’ I find this speculation to be plausible, but I do not pursue it here.
Examples where almost modifies generalized quantifiers on the negative scale (other than nobody) also exist on the internet, although they seem a bit marginal to me:
- (22)
- This means there are almost fewer than 1 million veterans remaining of the 16 million who served our nation in World War II.
- (http://www.southcoasttoday.com/article/20141209/OPINION/141209484)
- (23)
- At this point, we have fewer than 40 days of walking and almost fewer than 600 miles to go,
- (https://stormingjericho.com/saying-hi-ohio/)
In these examples the generalized quantifier X which is near Q is less than Q on the negative scale in (11b).
5. nowhere near
The semantic value in (8) involves existential quantification over generalized quantifiers. There are other scalar modifiers that are more transparently quantificational. Consider negative scalar modifiers, such as nowhere near, which seems to have a compositional interpretation (contra Morzycki 2001: 322). near is a relation between generalized quantifiers, and nowhere quantifies over points on the scale of generalized quantifiers. So, the expression in (24) has the truth conditions in (25):
- (24)
- Nowhere near everybody showed up.
- (25)
- ¬ƎX[near(X, ⟦everybody⟧) ∧ X(⟦showed up⟧)]
The question is what counts as near in (25). The use of the phrase nowhere near seems to push what counts as near to a lower threshold than the use of almost. If 80% or more counts as near, then anything less than 80% counts as nowhere near.
I will now show how to derive (25) compositionally given the analysis of scalar modifiers in this paper. I assume that nowhere near everybody has the following structure:
- (26)
- [DP [NEG SOME] [NP where [PP near everybody]]]
In other words, near everybody is a PP modifier of a noun where denoting the set of points on the positive scale of generalized quantifiers (each of which has as its restriction the set of people). On analyzing no as negation modifying SOME, see Collins and Postal 2014.
And I assume the following semantic values:
- (27)
- a.
- b.
- c.
- d.
- e.
- ⟦NEG⟧
- ⟦SOME⟧
- ⟦where⟧
- ⟦near⟧
- ⟦everybody⟧
- =
- =
- =
- =
- =
- λX.λQ.λP.¬X(Q)(P)
- λQ.λP.ƎX[Q(X) ∧ X(P)]
- λQ.positive-scale(Q)
- λQ.λX.near(X,Q)
- λP.∀x[person(x)
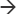 P(x)]
P(x)]
NEG in (27a) is the semantic value of negation, which directly modifies SOME (as opposed to negation in (5) which modifies the entire universal quantifier phrase, the distinction is not relevant to this paper). The first argument of SOME is a predicate of generalized quantifiers and the second argument is a predicate of individuals. where is a predicate of generalized quantifiers so its type is <<<e,t>,t>,t>. near is a relation between generalized quantifiers of type <<<e,t>,t>, <<<e,t>,t>,t>>.
The only semantic value that needs comment is (27b). Compare (27b) to the regular semantic value of some quantifying over individuals:
- (28)
- a.
- b.
- ⟦some⟧
- ⟦SOME⟧
- =
- =
- λQ.λP.Ǝx[Q(x) ∧ P(x)]
- λQ.λP.ƎX[Q(X) ∧ X(P)]
The reason for the difference is that English some quantifies over individuals, and those individuals satisfy the predicate P. SOME in (28b) quantifies over generalized quantifiers. And those generalized quantifiers must be satisfied by predicate P as their argument.
The compositional calculation is shown below:
- (29)
- a.
- b.
- c.
- d.
- e.
- ⟦near⟧(⟦everybody⟧)
- ⟦where⟧(⟦near everybody⟧
- ⟦NEG SOME⟧
- ⟦(26)⟧
- ⟦(24)⟧
- =
- =
- =
- =
- =
- λX.near(X, λP.∀x[person(x)
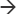 P(x)])
P(x)]) - λQ.[positive-scale(Q) ∧ near(Q, λP.∀x[person(x)
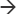 P(x)])
P(x)]) - λQ.λP.¬ƎX[Q(X) ∧ X(P)]
- λP.¬ƎX[positive-scale(X) ∧ near(X, λP.∀x[person(x)
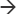 P(x)]) ∧ X(P)]
P(x)]) ∧ X(P)] - ¬ƎX[positive-scale(X) ∧ near(X, λP.∀x[person(x)
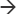 P(x)]) ∧ X(⟦showed up⟧)]
P(x)]) ∧ X(⟦showed up⟧)]
Alongside of nowhere near, as in (30a), there are also expressions like (30b):
- (30)
- a.
- b.
- I saw nowhere near every student.
- I didn’t see anywhere near every student.
Following Collins and Postal 2014, the structure of (30b) is:
- (31)
- I NEG1 see [[<NEG1> SOME] [where near every student]]
In this structure, <…> stands for an unpronounced occurrence. In this case NEG1 raises from a position modifying SOME to a post-auxiliary (post T) position. Examples like (30b) arise when NEG1 raises from the DP object, and SOME is spelled out as any (See Collins and Postal 2014 for details). (30a) and (30b) have the same interpretation since they both involve the same negative quantifier ([NEG SOME]) quantifying over the same set.
6. Survey
The analysis in section 5 of nowhere near everybody brings up the question of the range of similar complex scalar modifiers. To address this issue, I administered a survey to 15 people asking for acceptability judgments for various combinations of complex scalar modifiers with quantifier phrases. The people surveyed were all linguists. Of the 15 who took the survey, two failed to properly follow the instructions and so were excluded. Of the remaining, I only report below on the 12 who speak some variety of American English.
The instructions were the following: “This is an informal judgment survey about scalar modifiers of quantifier phrases. Please rate each sentence from 1 (unacceptable) to 5 (acceptable).” The survey was sent out to the individual people by e-mail, and the responses were received by e-mail.
In Figure 1, I give the actual ratings (anonymized) and the average of the ratings for each question. The notion 5[a] means that respondent [a] gives a rating of 5 to that particular sentence. Translating 4/5 as acceptable (OK) and 1/2 as unacceptable (*), I also present an idealized version of the results in the last column.
The survey in Figure 1 yielded the following minimal pair:
- (32)
- a.
- b.
- Nowhere near everybody will be at the party.
- *Somewhere near everybody will be at the party.
This contrast is surprising. One reason that the contrast is surprising is that I showed in section 5 that (32a) has a compositional interpretation, so we might expect such a compositional interpretation to extend to (32b). Another reason the contrast in (32) is surprising is that in the domain of physical location, both of the following are possible:
- (33)
- a.
- b.
- I parked nowhere near here.
- I parked somewhere near here.
I do not at the present time have any convincing analysis of the contrast in (32). But I note that a similar contrast applies in several other cases (personal communication, Richard Kayne and Paul Postal respectively):
- (34)
- a.
- b.
- John is nowhere near as smart as Bill.
- *John is somewhere near as smart as Bill.
- (35)
- a.
- b.
- He is nowhere near a .300 hitter.
- *He is somewhere near a .300 hitter.
The unacceptability of somewhere near everybody parallels the unacceptability of somewhere around everybody. I do not have an analysis of either at the time.
- (36)
- a.
- b.
- *Somewhere near everybody was at the party.
- *Somewhere around everybody was the party.
The survey shows that the following sentences involving nowhere around are all unacceptable:
- (37)
- a.
- b.
- c.
- *Nowhere around everybody will be at the party.
- *Nowhere around half of the people will be at the party.
- *Nowhere around nobody will be there.
These facts suggest that around is a positive polarity item that cannot be found in the scope of negation. Such an analysis is supported by the unacceptability of (38), which, uttered out of the blue, is degraded.
- (38)
- *I didn’t see around 10 rabbits.
In fact, (38) is only unacceptable on a low scope interpretation: “It is not the case that there were around 10 rabbits that I saw.” On a high scope interpretation, it is much better: “There were around 10 rabbits that I didn’t see.” These facts are consistent with around being a PPI.
In the survey, the following sentences involving half the people are acceptable:
- (39)
- a.
- b.
- c.
- Nowhere near half of the people will be at the party.
- Somewhere near half of the people will be at the party.
- Somewhere around half of the people will be at the party.
These facts generally support the analysis proposed here. For example, (39c) could be given a compositional analysis similar to the one given in (29) above.
- (40)
- a.
- b.
- Somewhere around half of the people showed up.
- ƎX[around(X, ⟦half of the people⟧) ∧ X(⟦showed up⟧)]
The difference between the metalanguage near and around is that around does not obey the condition in (21), so that (40a) is true if between 45% and 55% of the people showed up.
The following sentence involving a negative scalar modifier modifying a negative quantifier was rejected by the majority of respondents, but is predicted to be acceptable on my theory of scalar modifiers:
- (41)
- *Nowhere near nobody showed up.
The truth conditions should be:
- (42)
- ¬ƎX[near(X, ⟦nobody⟧) ∧ X(⟦showed up⟧)]
Suppose in this case that 20% or fewer counted as near. Then these truth conditions would be consistent with 21% or more of the people showing up.
Only three people rated the double negative in (41) to be 3 (on a scale of acceptability). However, one respondent commented on the importance of prosody. I suggest the problem with (41) is the presence of double negation. Even straightforward sentences like the following are not easy to judge out of the blue, because they involve double negation:
- (43)
- Nobody saw nobody.
- Intended: “Everybody saw somebody.”
Just like double negation is improved by context and prosody, the double negation in (41) seems to be improved by context and prosody. Consider the following dialogue between person A and person B (based on a suggestion by Larry Horn):
- (44)
- A:
- B:
- Nobody at all showed up at my party.
- Nowhere NEAR nobody showed up, the party was packed.
7. absolutely
Consider now absolutely as a scalar modifier:
- (45)
- Absolutely everybody showed up.
I propose that absolutely denotes the identity function:
- (46)
- ⟦absolutely⟧ = λQ.Q
However, this semantic value does not account for the following contrast:
- (47)
- a.
- b.
- c.
- d.
- absolutely everybody was there.
- absolutely nobody was there.
- *absolutely half of the people were there.
- *absolutely 75% of the people were there.
Such contrasts suggest that absolutely carries a presupposition that it only apply to endpoint quantifiers (see Horn 1972: 143; 2001: 237; 2005), where the notion of endpoint quantifier is defined with respect to the scales of generalized quantifiers in (11a,b):
- (48)
- An endpoint quantifier of S (a scale of generalized quantifiers) occupies the greatest position on the scale.
Given this definition, the semantic value of absolutely is (49a) (or more formally (49b)), where S is a contextually given scale of generalized quantifiers.
- (49)
- a.
- b.
- ⟦absolutely⟧
- ⟦absolutely⟧
- =
- =
- λQ:Q is the endpoint of S.Q
- λQ:∀X[X ε S
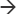 X ≤ Q].Q
X ≤ Q].Q
Paul Postal suggests that there is also an element of certainty of judgment in the semantics of absolutely, so that (45) implies that I am certain that everybody showed up. This implication is not captured in (49).
(49) predicts that combining almost and absolutely should be OK:
- (50)
- Almost absolutely everybody showed up.
In (50), absolutely everybody denotes the same generalized quantifier that everybody does, and so absolutely everybody can be modified by almost.
While the combination in (50) sounds a bit strained, there are actually a fair number of Google hits on the internet:
- (51)
- Almost absolutely everyone has their own website, be it a corporate website or a private web page.
- (https://universeinform.com/web-design-and-development-software/)
The reverse combination is much worse:
- (52)
- *Absolutely almost everybody showed up.
The unacceptability of (52) follows from the fact that almost everybody, as opposed to everybody, is not an endpoint quantifier.
The analysis in (49) also predicts that absolutely everybody can be modified by negation. Such examples are easy to find on the internet, and sound natural:
- (53)
- Strange as it may seem, not absolutely everybody is hunting for rare Pokémon on their phones right now
- (https://www.sciencealert.com/scientists-have-found-a-weird-glowing-purple-blob-on-the-ocean-floor)
- (54)
- But not absolutely everybody who voted Labour in Canterbury has mental health problems.
- (https://www.thesun.co.uk/news/3777032/if-the-tories-want-to-win-back-canterbury-they-should-wait-until-the-students-are-off-on-holiday/)
Once again, these sentences are OK because absolutely everybody has the same denotation as everybody, and everybody can be modified by negation (since it is a generalized quantifier of type <<e,t>,t>).
8. Negative Polarity Items
Universal quantifier phrases modified by almost license negative polarity items in their restriction:
- (55)
- a.
- b.
- Everybody who has ever been to France smokes.
- Almost everybody who has ever been to France smokes.
However, the restriction of the modified universal quantifier phrase does not allow downward entailing inferences. For example, (56a) does not entail (56b):
- (56)
- a.
- b.
- Almost everybody who owns a car is happy.
- Almost everybody who owns a Jaguar is happy.
If the number of Jaguar owners is small, it might be that there are hardly any happy Jaguar-owners, but still almost all the car owners are happy. The reason for this shift, on the theory presented in section 2, is that the scale of generalized quantifiers is calculated with respect to the restriction. The restriction in (56a) is the set of people who own a car, and the restriction in (56b) is the set of people who own a Jaguar (a much smaller set). Almost everybody who owns a car might be two billion people, but almost everybody who owns a Jaguar might be two thousand people. Even if every Jaguar owner was unhappy, it would not make much of dent in the number of happy car owners.
If the restriction of the modified quantifier phrase in (56) is not a downward entailing context, then why are NPIs licensed in (55b)? I propose that the answer can be found in the proposed structure of the modified quantifier phrases (see section 2 for proposal):
- (57)
- [almost [everybody who has ever been to France]]
Consider (57) from the point of view of the following condition (for discussion see Collins and Postal 2014: 72):
- (58)
- “A negative-polarity item is acceptable only if it is interpreted in the scope of a downward-entailing expression.” (from Ladusaw 2002: 467)
Crucially, this formulation makes no reference to whether the overall sentential context of the NPI is downward entailing or not. Therefore, since the restriction of a universal quantifier phrase is a downward entailing context, the negative polarity item is licensed (for related discussion, see Hoeksema 1986 and Homer 2020).
As discussed in Collins (2020) (see also Horn 1996), a similar issue arises for negated universal quantifier phrases:
- (59)
- a.
- b.
- c.
- Every professor who has ever been to France smokes.
- *Some professors who have ever been to France smoke.
- Not every professor who has ever been to France smokes.
Collins (2020: 239) argues that if the constituent structure of the negated quantifier phrases is [not [every professor who has ever been to France]], then the NPI is licensed since the NPI ever is in the restriction of the universal quantifier. “The calculation of the relevant DE-ness is not based on properties of the whole sentence.”
The distribution of NPIs in the restriction of modified quantifier phrases (modified by either negation or almost) confirms the basic syntactic and semantic proposals of this paper.
9. Existential Quantifier Phrases
As opposed to universal and negative quantifier phrases, existential quantifier phrases do not admit scalar modifiers (see Horn 2005):
- (60)
- a.
- b.
- c.
- *Almost some boy was there.
- *Absolutely some boy was there.
- *Nowhere near some boy was there.
- (61)
- a.
- b.
- c.
- *Almost some boys were there.
- *Absolutely some boys were there.
- *Nowhere near some boys were there.
- (62)
- a.
- b.
- c.
- *Almost some of the boys were there.
- *Absolutely some of the boys were there.
- *Nowhere near some of the boys were there.
- (63)
- a.
- b.
- c.
- *Almost a boy was there.
- *Absolutely a boy was there.
- *Nowhere near a boy was there.
- (64)
- a.
- b.
- c.
- *Almost boys were there.
- *Absolutely boys were there.
- *Nowhere near boys were there.
- (65)
- a.
- b.
- c.
- *Almost several boys were there.
- *Absolutely several boys were there.
- *Nowhere near several boys were there.
One possibility is that these examples are all unacceptable because indefinites are not quantificational (rather, indefinite DPs would be of type <e,t> denoting predicates). As predicates, they could not be modified by a scalar modifier defined for generalized quantifiers. However, I propose a different account based on the assumption that indefinite DPs denote generalized quantifiers.
Since absolutely can only modify endpoint quantifiers (defined as the highest point on the scale), data in the (b) sentences follows from the fact that existential generalized quantifiers are not endpoint quantifiers.
As for the (a) sentences, consider the following contrast:
- (66)
- a.
- b.
- c.
- *Almost one boy was there.
- ?Almost two boys were there.
- Almost ten boys were there.
(66c) is fine and would be true if eight or nine boys were there. (66b) seems acceptable, but odd because it implies that one boy was there (so one could have said one boy, instead of the awkward almost two boys). Now consider (66a). According to the condition in (21), near(X,Q) entails that X is less than Q on the positive scale. But there is no X less than the denotation of one boy on the positive scale.
In other words, scalar modification cannot yield a value that jumps between the two scales in (11), but only moves around on a single scale (see Hitzeman (1992: 231) for a similar analysis of facts like (60–65)). A similar explanation holds for all the (a) sentences in (60–64). In each case, almost is modifying the lowest element on the positive scale of generalized quantifiers.
I do not attempt to account for the unacceptability of almost many boys here (see Hitzeman 1992: 231). Unlike some, many is not the lowest element on the positive scale, so it cannot be excluded in the same way as (60–65).
The condition in (21) allows the following examples:
- (67)
- a.
- b.
- c.
- d.
- Almost half of the people were there.
- Almost 75% of the people were there.
- Nowhere near half of the people were there.
- Nowhere near 75% of the people were there.
In none of these cases does the quantifier phrase denote the lowest point on the relevant scale, and so it can be modified by almost.
Consider now the lowest element of the negative scale not everybody:
- (68)
- a.
- b.
- c.
- *Almost not every student was there.
- *Absolutely not every student was there.
- *Nowhere near not every student was there.
Once again, the unacceptability of (68b) follows from the fact that not everybody is not an endpoint generalized quantifier, and so it cannot be modified by absolutely.
According to the condition in (21), near(X,Q) entails that X is less than Q on the negative scale. But there is no X less than the denotation of not everybody on the negative scale. So (68a,c) are excluded.
Free choice any quite productively takes scalar modifiers:
- (69)
- a.
- b.
- c.
- Almost anybody should be able to do that.
- Absolutely anybody should be able to do that.
- *Nowhere near anybody should be able to do that.
(69b) strongly suggests that free choice anybody is an endpoint generalized quantifier on the positive scale (equivalent to everybody), but I do not pursue the issue here (see Horn 2005 for discussion). The unacceptability of (69c) is a mystery.
10. Conclusion
I have analyzed the syntax and semantics of scalar modifiers of quantifier phrases. The syntax is based on the structure [almost DP], analogous to the structure of negated quantifier phrases [not DP] in the framework of Collins and Postal 2014. The semantics is stated in terms of scales of generalized quantifiers.
A future topic will be to extend this kind of analysis to other modified elements. As noted by Morzycki (2001: 310): “Almost modifiers constitute a natural class distinguished by position and interpretation, whose members may occur in left peripheral positions across a range of syntactic categories.” Some examples are the following:
- (70)
- a.
- b.
- c.
- d.
- e.
- f.
- g.
- h.
- i.
- j.
- k.
- The cup is almost full.
- The cup is absolutely full.
- The cup is nowhere near full.
- Dinner is almost ready.
- John has almost finished his homework.
- He almost died.
- Paris is near Versailles.
- He is almost there.
- He is almost always late.
- He is almost never late.
- He is absolutely never late.
- (adjective)
- (adjective)
- (adjective)
- (adjective)
- (VP)
- (VP)
- (Locative)
- (Locative)
- (Adverb)
- (Adverb)
- (Adverb)
Morzycki proposes that one can account for cross-categorial almost in terms of intensional similarity (similarity of worlds). But no notion of intensional similarity was needed for scalar modification of quantifier phrases on my analysis. Rather, only the extensional notion of nearness on a scale of generalized quantifiers was needed. I leave to future work whether nearness on a scale will also account for the other uses of almost in (70).
Acknowledgements
I thank Richard Kayne, Larry Horn and Paul Postal for discussions of the issues in this paper. I also thank the respondents of my acceptability judgments survey. I am grateful to the editor Johan Rooryck and three reviewers who provided me with much useful feedback.
Competing interests
The author has no competing interests to declare.
References
Chierchia, Gennaro & Fox, Danny & Spector, Benjamin. 2012. Scalar Implicatures as a Grammatical Phenomenon. In Maienborn, Claudia & von Heusinger, Klaus & Portner, Paul (eds.), Semantics: An International Handbook of Natural Language Meaning, vol. 3, 2297–2331. Mouton de Gruyter.
Collins, Chris. 2016. Not even. Natural Language Semantics 24. 291–303. DOI: http://doi.org/10.1007/s11050-016-9124-5
Collins, Chris. 2020. Outer Negation of Universal Quantifier Phrases. Linguistics and Philosophy 43. 233–246. DOI: http://doi.org/10.1007/s10988-019-09269-4
Collins, Chris & Postal, Paul M. 2014. Classical NEG Raising. Cambridge: MIT Press. DOI: http://doi.org/10.7551/mitpress/9780262027311.001.0001
Crnič, Luka. 2018. A Note on Connected Exceptives and Approximatives. Journal of Semantics 35. 741–756. DOI: http://doi.org/10.1093/jos/ffy011
Haegeman, Liliane. 2012. Adverbial Clauses, Main Clause Phenomena, and the Composition of the Left Periphery. The Cartography of Syntactic Structures, Volume 8. Oxford: Oxford University Press. DOI: http://doi.org/10.1093/acprof:oso/9780199858774.001.0001
Heim, Irene & Kratzer, Angelika. 1998. Semantics in Generative Grammar. Oxford: Blackwell Publishers.
Hitzeman, Janet. 1992. The Selectional Properties and Entailments of ‘Almost’. In Canakis, Costas P. & Chan, Grace P. & Denton, Jeannette Marshall (eds.), Papers from the 28th Regional Meeting of the Chicago Linguistics Society.
Hoeksema, Jack. 1986. Monotonicity Phenomena in Natural Language. Linguistic Analysis 16. 25–40.
Homer, Vincent. 2020. Negative Polarity. In Gutzmann, Daniel & Matthewson, Lisa & Meier, Cécile & Rullmann, Hotze & Zimmermann, Thomas Ede (eds.), The Wiley Blackwell Companion to Semantics. John Wiley and Sons. DOI: http://doi.org/10.1002/9781118788516.sem057
Horn, Laurence. 1972. On the Semantic Properties of Logical Operators in English. UCLA Dissertation, UCLA.
Horn, Laurence. 1996. Exclusive Company: Only and the Dynamics of Vertical Inference. Journal of Semantics 13. 1–40. DOI: http://doi.org/10.1093/jos/13.1.1
Horn, Laurence. 2001. A Natural History of Negation. Stanford: CSLI.
Horn, Laurence. 2005. Airport 86’ Revisited: Toward a Unified Indefinite any. In Carlson, Greg & Pelletier, Francis Jeffrey (eds.), The Partee Effect, 179–205. Stanford: CLSI.
Horn, Laurence. 2011. Almost Forever. In Yuasa, Etsuyo & Bagchi, Tista & Beals, Katharine (eds.), Pragmatics and Autolexical Grammar: In Honor of Jerry Saddock. Amsterdam: John Benjamins. DOI: http://doi.org/10.1075/la.176.01hor
Jayez, Jacques & Tovena, Lucia M. 2008. Presque and almost: How Argumentation Derives from Comparative Meaning. In Bonami, Olivier & Cabredo Hofherr, Patricia (eds.), Empirical Issues in Syntax and Semantics, 1–20.
Morzycki, Marcin. 2001. Almost and its Kin, Across Categories. In Hastings, Rachel & Jackson, Brendan & Zvolensky, Zsófia (eds.), Semantics and Linguistic Theory XI, 306–325. DOI: http://doi.org/10.3765/salt.v11i0.2839
Nouwen, Rick. 2006. Remarks on the Polar Orientation of almost. Linguistics in the Netherlands 2006. 162–173. DOI: http://doi.org/10.1075/avt.23.17nou
Partee, Barbara & Rooth, Mats. 1983. Generalized Conjunction and Type Ambiguity. In Portner, Paul and Partee, Barbara H. (eds.), Formal Semantics: The Essential Readings, 334–356. Oxford: Blackwell Publishers. DOI: http://doi.org/10.1002/9780470758335.ch14
Penka, Doris. 2005. Almost: a Test? Dekker, Paul & Franke, Michael (eds.) Proceedings of the Fifteenth Amsterdam Colloquium, 179–184. Amsterdam: University of Amsterdam.
Penka, Doris. 2006. Almost There: The Meaning of almost. Proceedings of the Sinn and Bedeutung 10. 275–286. DOI: http://doi.org/10.21248/zaspil.44.2006.317
Penka, Doris. 2011. Negative Indefinites. Oxford: Oxford University Press. DOI: http://doi.org/10.1093/acprof:oso/9780199567263.001.0001
Sadock, Jerrold. 1981. Almost. In Cole, Peter (ed.), Radical Pragmatics, 257–271. New York NY: Academic Press.
Spector, Benjamin. 2014. Global Positive Polarity Items and Obligatory Exhausitivity. Semantics and Pragmatics 7. 1–61. DOI: http://doi.org/10.3765/sp.7.11
Zanuttini, Rafaella. 1991. Syntactic Properties of Sentential Negation: A Comparative Study of Romance Languages. Doctoral dissertation, University of Pennsylvania.


