1 Introduction
Reduplication is a common morphological process of copying, with a wide-ranging typology. In theoretical linguistics, reduplication has been formalized in multiple different ways (Inkelas & Downing 2015a; b). However, there is relatively little work on the computational or mathematical aspects of reduplication and reduplicative typology. There is even less work linking and evaluating the computational expressivity of reduplicative theories against the expressivity of the attested typology.
Formalizing theories of reduplication raises the issue of how theories represent the idea of not only copying segments, but also the sequencing of repeated segments within a reduplicative construction. These issues bear on the role of sequencing and repetition in cognition (Endress et al. 2007; Buzsáki & Tingley 2018; Moreton et al. 2021), as well as how machine learning methods infer these constructions (Dolatian & Heinz 2018a; Beguš 2021; Nelson et al. 2020; Prickett et al. 2022).
In this paper, we lay out the computational aspects of reduplication and reduplicative typology, and classify a wide array of reduplicative theories. The end result is that most of these theories are far more expressive than the typological phenomena require. This is unlike non-reduplicative phenomena and theories, both of which occupy similarly restricted computational function classes.
The organization of this paper follows our argument. §2 discusses how copying processes show a cline of computational expressivity based on a) the size of the copied substring, and b) whether the input contains explicit information on how many times to apply copying. We show that both of these dimensions reflect the distinction between properly regular or properly polyregular functions. This regular vs. polyregular division distinguishes the phenomenon of reduplication itself from many linguistic theories of reduplication. Using this landscape of function classes, we go over the computational and mathematical properties of natural language reduplication.
Having clarified the generative capacity of reduplication as a phenomenon, in §3 we classify the range of reduplicative theories to determine whether they are more computationally complex than needed, i.e. they treat reduplication as a more powerful function type than its inherent type. The key property is whether the input contains a countable number of reduplicative instructions (polyregular) or not (regular). This is because the theory involves counting the number of these instructions in order to know how many copies are generated. Such theories are more expressive than reduplication because they utilize counting. This includes item-and-arrangement theories like templatic reduction (Marantz 1982) and variants of Base-Reduplicant Correspondence (BRCT: McCarthy & Prince 1995). This reliance on counting is clearer for cases such as triplication. In contrast, some theories are properly regular because they do not utilize counting. This group includes item-and-process based theories whereby all counting is pre-compiled into the function, such as Word-Formation Rules (Aronoff 1976), Transformation Rules (Carrier 1979), and variants of BRCT. We then overview the representational issues in multiple reduplication in §4. Overall discussions are in §5. We conclude in §6.
From this paper, one might conclude that “Because theory X matches reduplication better, X is a superior theory to all other theories.” It is not the goal of this paper to draw such conclusions. Instead, this paper’s goal is to specify exactly how theories may differ. We want to showcase the insights gained by combining typological, mathematical, theoretical perspectives on natural language.
2 Generative capacity of reduplication
The generative capacity of a grammar indicates what types of patterns it can or cannot model. Similarly, the generative capacity of a pattern indicates what grammars can model it. In this section, we go over the generative capacity of reduplication, based on the size of the generated copies and the number of copies. We first set up our basic formal classes of functions in terms of finite state transducers. We then apply these functions to describe total reduplication (ia), partial reduplication (ib), and triplication (ic). We discuss the generative capacity of each phenomenon on its own.
- i.
- a.
- Indonesian (Cohn 1989: 308)
- buku→buku∼buku
- wanita→wanita∼wanita
- ‘book’→’books’
- ‘woman’→’women’
- b.
- Agta (Moravcsik 1978: 311)
- takki→tak∼takki
- ‘leg’→’legs’
- c.
- Taiwanese (Zhang & Lai 2007: 34)
- pʰoŋ21→pʰoŋ51∼pʰoŋ21
- pʰoŋ21→pʰoŋ51∼pʰoŋ51∼pʰoŋ21
- ‘blown-up’→’somewhat blown-up’
- ‘blown-up’→’very blown-up’
2.1 Functions and transducers
At the computational level, functions on words are defined by string-to-string transductions (also called mappings or transformations). Transductions have many characterizations, but in linguistics the most popular description is given using transducers. Informally, transducers are idealized machines that transform an input string to an output string. They extend automata (acceptors) with outputs on their transitions. They can be seen as Turing machines with a read-only input tape initially filled with the input word, and a write-only output tape on which to write the output word.
In this paper we will consider three important classes of transducers with a finite number of states: one-way transducers, two-way transducers, and two-way transducers with pebbles, summarized in Table 1. The table lists various formal properties that we will discuss and expand on throughout this section.
Classes of transducers, their functions, and their properties.
| Transducer type | Machine properties | Computed function | Function properties |
| pebble 2-way FST | input head moves left/right mark the input with pebbles | polyregular function | polynomial growth size |
| 2-way FST | input head moves left/right | regular function | linear growth size, non-order preserving |
| 1-way FST | input head moves right | rational function | linear growth size, order-preserving |
For each class, the output head is assumed to move only to the right. For the class of one-way transducer, the input head is also restricted to move to the right on the input tape; for the other classes, the input head can move left or right. These three classes of machines yield three classes of functions: rational, regular, and polyregular. The rational functions can model all attested morphological and phonological processes except for total reduplication (Kaplan & Kay 1994; Roark & Sproat 2007). The regular functions are strictly more expressive than the rational functions, and they can model total reduplication.1 And the most expressive is the class of polyregular functions, which has received more attention in recent years in computer science but not computational linguistics. These different functions display different formal properties that we discuss later.
Note that all the formal results in this section are from the literature on mathematical linguistics or theoretical computer science (Filiot & Reynier 2016; Dolatian & Heinz 2020; Dolatian et al. 2021). We do not provide formal proofs nor do we explain them in mathematical depth. We instead focus on synthesizing all these pre-known results into a single self-contained body on reduplication.
2.2 Total reduplication is a regular function
Consider total reduplication, as in the Indonesian example (ia) of buku∼buku ‘books’. Computationally, total reduplication involves making two copies of the input. The process creates exactly one extra copy of the input string. The input string can be of any size.
As a copying function, total reduplication introduces a single extra copy in the output. Such copying functions belong to the class of Regular functions. A regular function can copy a string of unbounded size but only a linearly bounded number of times. Given a string w, the process of generating one extra copy w → ww is a regular function. For a regular function, the size of the output string grows at most linearly with the size of the input string |w|, that is . For total reduplication of an input string w, the size of the output ww is exactly 2|w|. Mnemonically, total reduplication is a case of ‘unbounded fixed-n copying’ where we copy the word to create exactly n = 1 extra copy.
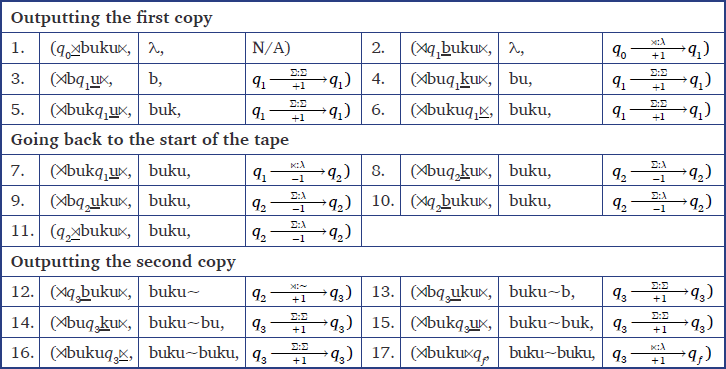
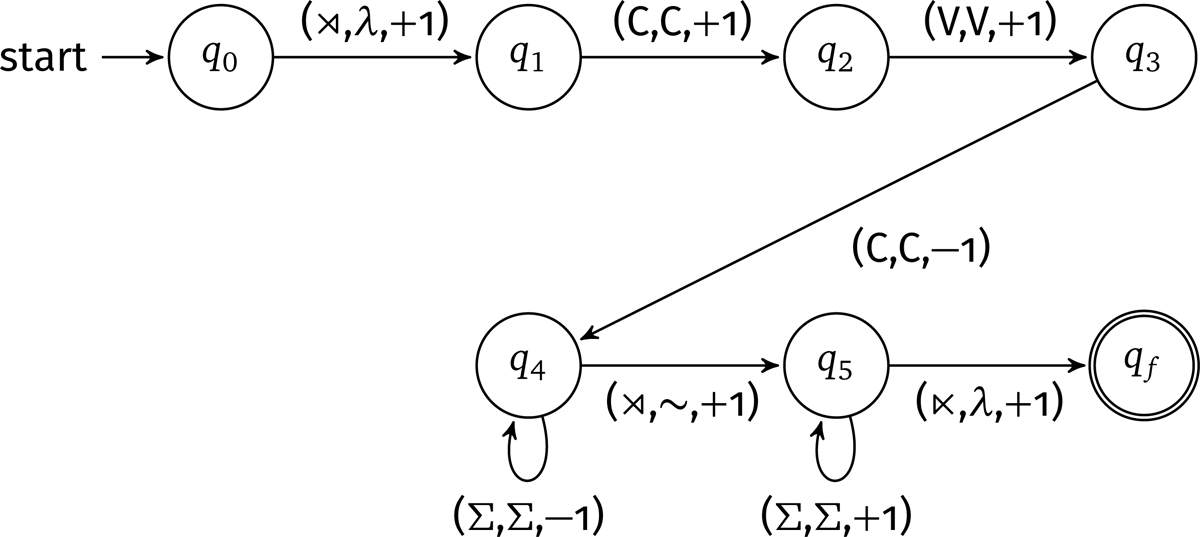
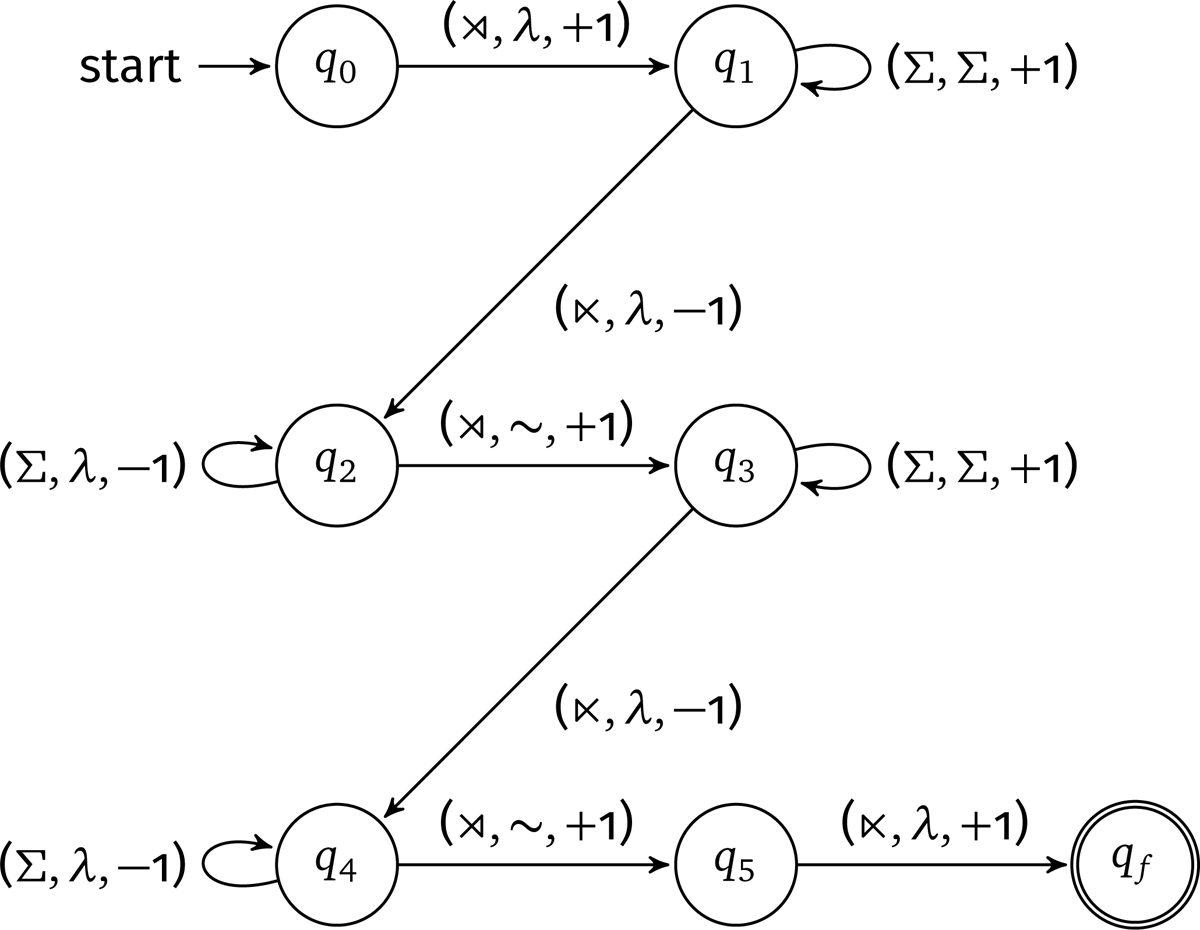
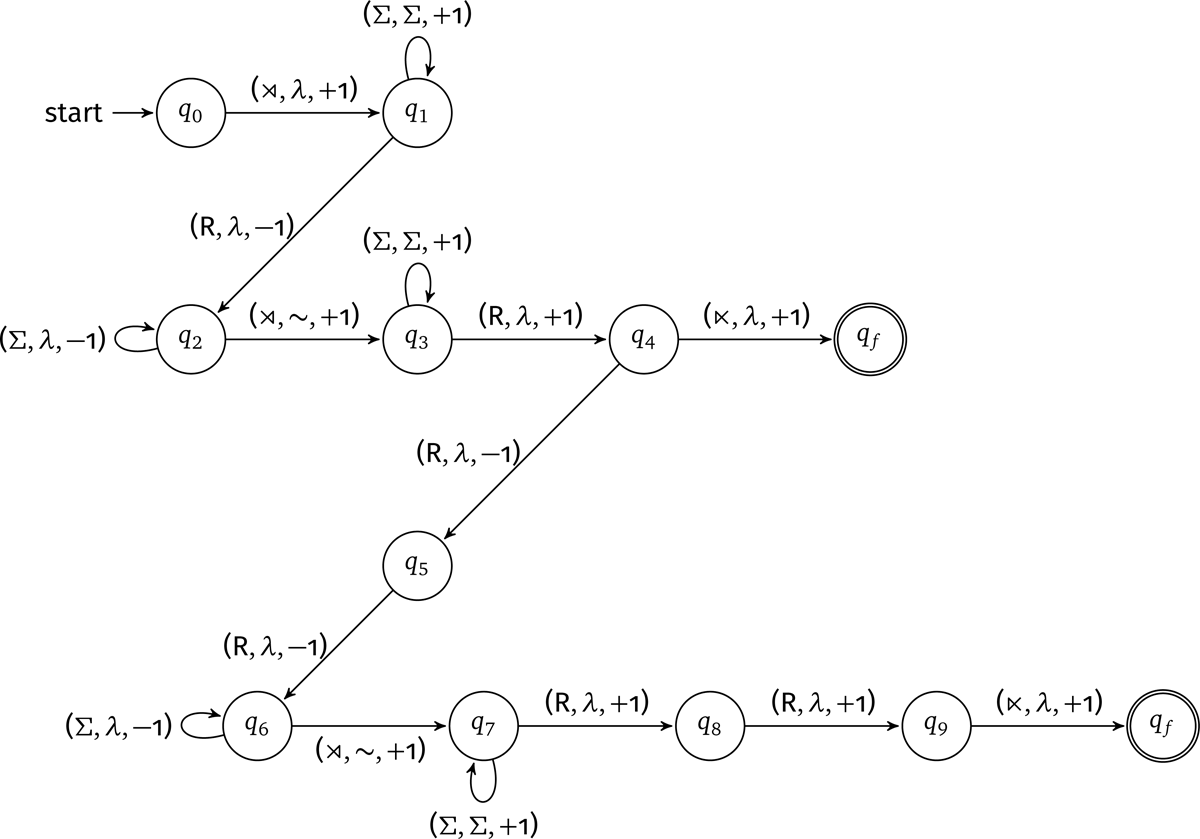
This property of linear-growth rate allows many equivalent characterizations of regular functions, in terms of logic, algebra, and automata (Engelfriet & Hoogeboom 2001; Filiot & Reynier 2016). The one most relevant for linguistics is that Regular functions are exactly the functions computed by deterministic 2-way FSTs (Hopcroft & Ullman 1969; Savitch 1982). The intuition is that each copy is made by the ability of a 2-way transducer to go back-and-forth over the input a bounded number of times while outputting. Figure 1 is a visual representation of a 2-way FST for total reduplication.
Before we demonstrate how this machine models total reduplication, consider the visual properties of the machine in Figure 1. Between any two nodes or states, there is a directed edge called the transition. For example, from state q0 to state q1, there is an edge labeled . The transition means that we read the symbol from the input, we generate an output symbol λ, and we move right (+1) on the input string. In this case, the symbol λ designates the empty string. Elsewhere in the graph, the symbol Σ designates any symbol in our input alphabet (that’s not a word boundary), and the symbol –1 designates moving leftward on the input string.
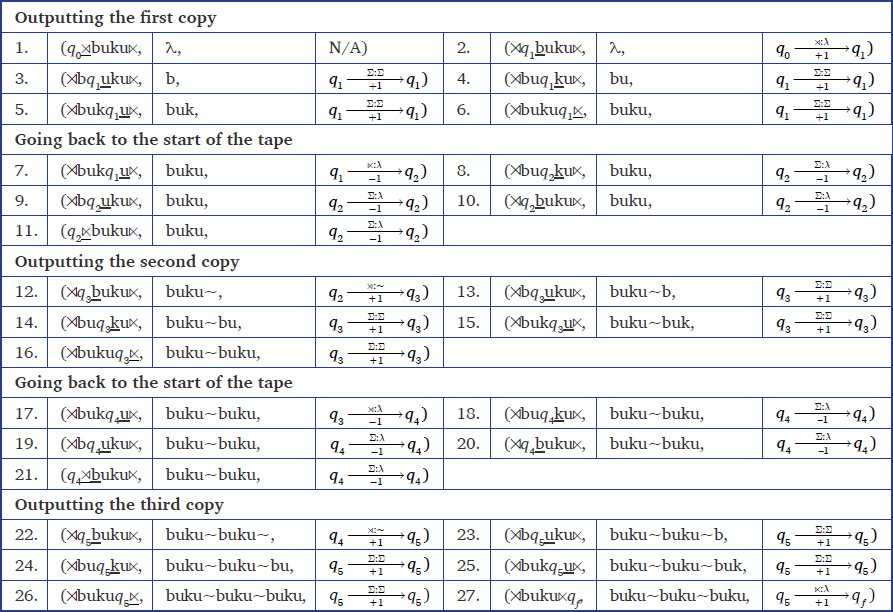
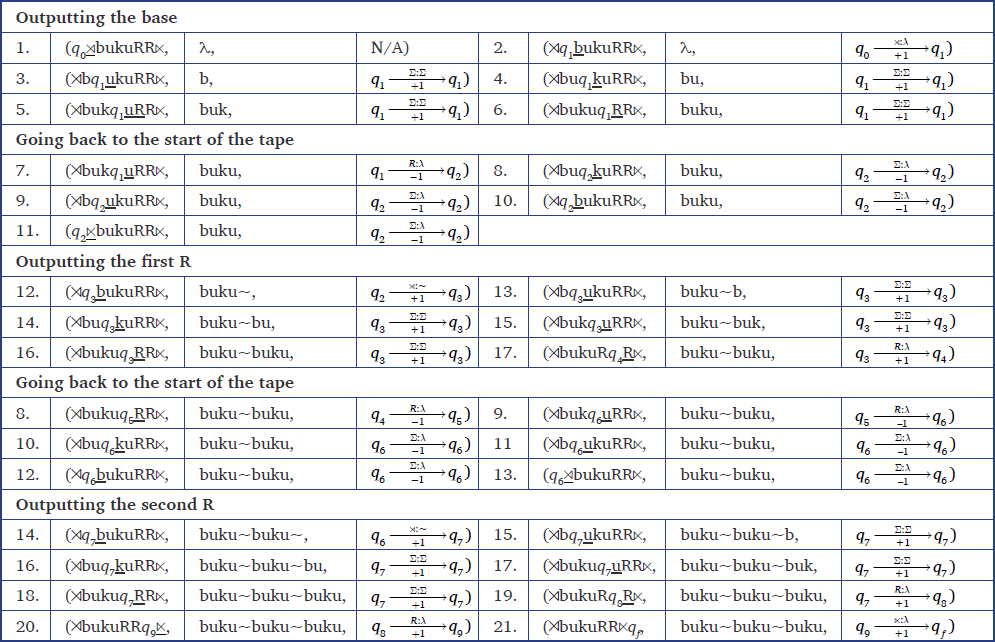
Let us see how this machine models total reduplication. Table 2 illustrates a derivation using this 2-way FST for the mapping buku→buku∼buku. The steps in our derivation tables have following format where the first element is the processed input string, the second is the current output string, and the third is the transition that was used to go from the previous step to the current step.
The input string is first padded with word boundaries . In step 1, the machine is in state q0. We use underlining to show what symbol is to be read next. The first symbol to read is . In step 2, we read , output nothing, move rightward on the input string, and then change to state q1. The next symbol to read is b. In steps 3–6, we iteratively move left-to-right (+1) on the input string, outputting any input symbol (Σ), and stay in state q1. This creates the first output copy. Then between step 6–7, we reach the end boundary , move to state q2, and we iteratively go right-to-left (–1) on the input string, outputting nothing until we reach the start boundary . At around steps 11–12, we read the state boundary , output the reduplicant boundary ∼, move to state q3, and then read the input string again from left-to-right (+1). Between steps 16–17, we reach the end boundary , output nothing, and we finish the transduction in the final state qf
Thus, total reduplication is a regular string-to-string function, requiring only the expressivity of a 2-way FST (Dolatian & Heinz 2018b; 2020).2
2.3 Partial reduplication is a regular function
Total reduplication is a regular function where we copy the entire input string exactly once. Now consider partial reduplication as in Agta initial-CVC reduplication: takki→tak∼takki (ib). In partial reduplication, a given morphological construction specifies the maximal size of the partial reduplicant. Although a cross-linguistic maximum is unclear, most attested cases of partial reduplication impose a bound that can vary from 1 to around 5 segments, or one to two syllables (Rubino 2013; Inkelas & Downing 2015b). For pluralization in Agta, this bound seems to be 3.
It is immediately clear that partial reduplication is also a regular function. Just like total reduplication, partial reduplication generates exactly one extra copy of the input string. This copy is however a substring of the input string.
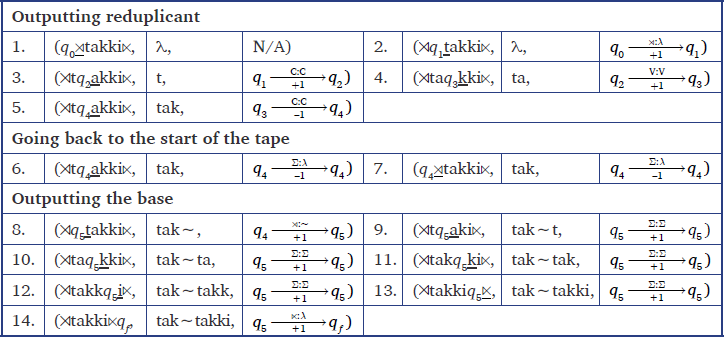
Figure 2 is a 2-way FST for partial reduplication with initial-CVC reduplication. The main difference between our 2-way FST for total (Figure 1) vs. partial reduplication (Figure 2) is the following. For total reduplication, the machine first reads and outputs the entire input string before returning to the start boundary . But for partial reduplication, the machine outputs the first CVC substring and then returns to the start boundary .
Table 3 illustrates a derivation using this 2-way FST for the mapping takki→tak∼takki. In steps 1–5, we output the first CVC substring (= the reduplicant). Steps 6–7 return to the start boundary . Finally, steps 8–14 output the input string (= the base).
Note that the above machines are for prefixal partial reduplication. Suffixal partial reduplication can also be modeled with such machines and functions. The difference would be the choice of directionality: do we read left-to-right up until the first CVC, or do we read right-to-left up until the final CVC.
Thus, like total reduplication, partial reduplication is a regular function. Furthermore, the bound on the size of the reduplicant means all partial reduplication types belong to a more restricted subclass of regular functions called rational functions. Rational functions can describe copying a substring of bounded size. Given a string w, the process of generating a copy w → uw where u is a fixed-size substring of w is a rational function. Given a string w of size |w|, the output string is at most the size 2|w|. For initial-CVC reduplication, the size of the output string is exactly |w|+3.
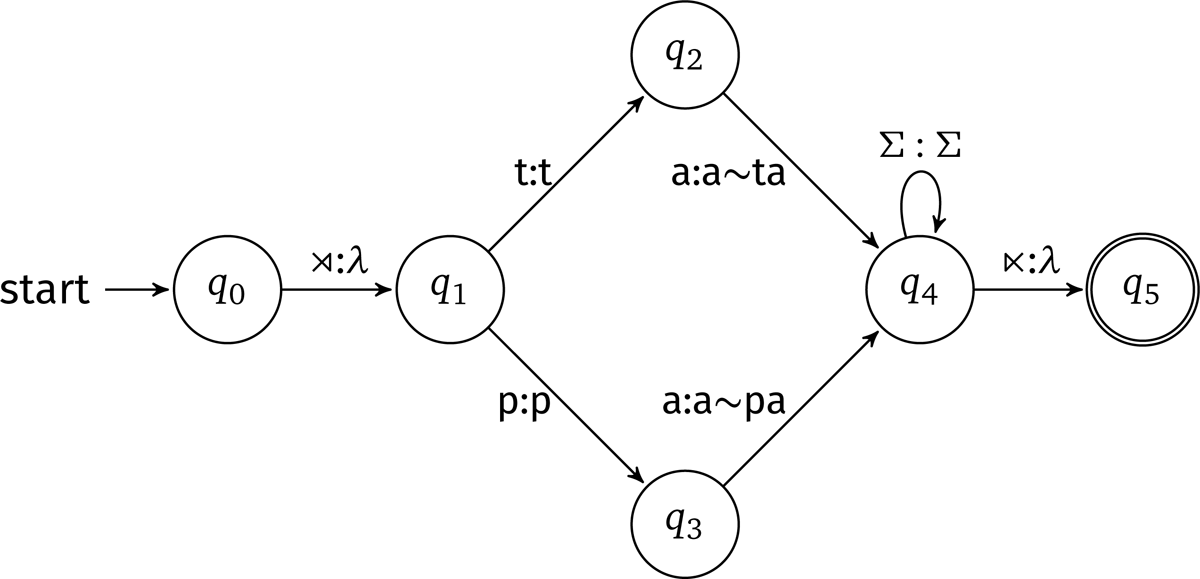
Rational functions are far more restricted than regular functions. They can be described by 1-way FSTs, among other logical and algebraic characterizations (Filiot & Reynier 2016). 1-way FSTs are a common tool enough so that that the prefix ‘1-way’ is usually omitted in publications in NLP and computational linguistics.3 For this reason, most computational work describes partial reduplication using 1-way FSTs (Roark & Sproat 2007; Chandlee & Heinz 2012). This situates partial reduplication alongside most other attested morphological and phonological processes (Johnson 1972; Koskenniemi 1983; Ritchie 1992; Kaplan & Kay 1994; Beesley & Karttunen 2003; Roark & Sproat 2007; Rogers & Pullum 2011; Heinz & Idsardi 2013; Rogers et al. 2013; Chandlee 2014; 2017; Chandlee & Heinz 2018; Chandlee et al. 2018). To illustrate, Figure 3 is a 1-way FST for partial reduplication with initial-CV reduplication, with a simple alphabet Σ = {p, t, a}. The machine works by reading the initial CV substring, memorizing it, and outputting twice. The machine cannot go back and forth on the input, but only move rightward.
Because partial reduplication requires that the copied substring has a fixed size (such as 2 for initial-CV, or 3 for initial-CVC), then partial reduplication is a rational function. Since every rational function is by definition a regular function, we stick to categorizing partial reduplication as a ‘regular function’ in order to clarify the connection between partial and total reduplication.4
2.4 Triplication is a regular function
So far, we discussed only reduplicative patterns where there is exactly one new copy that is generated. In spoken natural languages, most attested cases of reduplication involve adding only one copy, whether partial or total. For example, in the Indonesian case of total reduplication (ia), the additional copy is used to mark plurality. In some natural languages, a single morphosyntactic feature can instead be expressed by generating multiple copies (ii), such as adding two copies to mark intensity in Taiwanese.
- ii.
- a.
- Taiwanese (Zhang & Lai 2007: 34)
- pʰoŋ21→pʰoŋ51∼pʰoŋ21
- pʰoŋ21→pʰoŋ51∼pʰoŋ51∼pʰoŋ21
- ‘blown-up’→’somewhat blown-up’
- ‘blown-up’→’very blown-up’
- b.
- Mandarin (Zhang 1987: 308)
- ang→ang∼ang
- ang→ang∼ang∼ang
- ‘red’→’reddish’
- ‘red’→’extremely red’
Such cases of triplication are less common but attested in spoken natural languages, both as total copying as above or partial copying (Rai & Winter 1997; Rai et al. 2005).5 Triplication is very widespread in sign languages (Pfau & Steinbach 2006). It is used for pluralization, reciprocals, and various types of aspectual modification (Wilbur 2005).
Computationally, triplication of the entire input string is no more complex than total reduplication. As mentioned, given a string w, the process of generating one extra copy w → ww is a regular function. Likewise, the process of generating 2 extra copies w → www is a separate but still regular function.
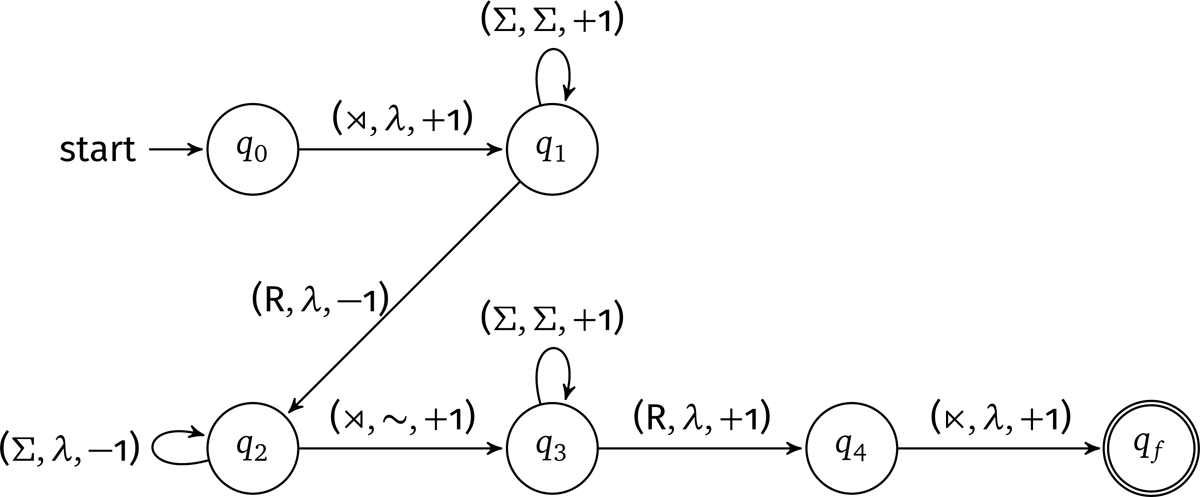
To illustrate, Figure 4 is a 2-way FST for triplication. This 2-way is larger than the one for total reduplication (Figure 1). The main difference is that we have an extra set of states q4, q5 that read the input string again for the third time in order to create an extra copy.
Table 4 illustrates a derivation using this 2-way FST for the hypothetical mapping buku→buku∼buku∼buku.
Although it may seem counter-intuitive, triplication is not more computationally complex than total reduplication. Informally, any function which generates n number of copies is regular as long the number of copies n is pre-determined and fixed.6 For triplication, the number of new copies (= 2) is still bounded for any particular process. In terms of output growth, triplication of a string w creates an output string of size 3|w|.
This is a crucial property for the computation of reduplicative morphology. If the function cannot predetermine the number of copies, i.e., we need to calculate and count how many copies to generate, then the function is not regular. For triplication, the relevant semantic feature is realized by a fixed number of multiple copies. However, there are few if any robust cases in spoken languages where a single feature (such as pluralization or continuativity) is realized by a variable number of copies without any difference in semantics, e.g., w → ww,www without a difference in meaning between ww and www. Recent corpus and elicitation data suggests that signers may variably mark plurals using two, three, or more copies in this way (van Boven 2021). Regardless, such a process is still a regular relation because there is a maximum bound. The difference between a function and a relation is that a function returns at most one output string, while a relation can return multiple, such as in the case of linguistic variation.
2.5 Polyregular computation and reduplication
As mentioned, the key property defining regular functions is that their output length may be at most a linear growth on the input (potentially even just a constant), such as 2|w| for total reduplication, 3+|w| for CVC partial reduplication, and 3|w| for triplication. In this section, we discuss more expressive functions that go beyond linear growth rates. These are polyregular functions. Crucially, reduplication is weaker than such functions.
For polyregular functions, the size of the output string can grow polynomially with respect to the size of the input string |w|, i.e. (|w|n) (Bojańczyk et al. 2019; Lhote 2020). The polynomial growth property enables many equivalent characterizations of polyregular functions, in terms of logic, algebra, and automata (Bojanczyk 2022). With respect to automata, polyregular functions are exactly the functions that can be computed by augmenting a 2-way FST with a set of “pebbles”, an analogous mechanism to a stack where some number k of markers are dropped and picked up along the input while it is being read. These pebbles are used as a type of memory device so that the machine can hop back and forth on the input tape, and remember its previous positions. Such “pebble transducers” exactly compute the polyregular functions.7
A type of copying function that is properly polyregular is what we call input-specified copying. Here, the input contains a string of instruction symbols R that determine how many copies of w will be generated. For these functions there is a dependency between the number of instructions R and the number of output copies.8
- iii.
- Unbounded input-specified copying
- wRn → wwn
- patipa r r →patipa∼patipa∼patipa
To illustrate why such input-specified copying is not a regular function, we provide example 2-way FSTs that approximate a polyregular function where one or two reduplication morphemes are input-specified. We formulate such functions below.
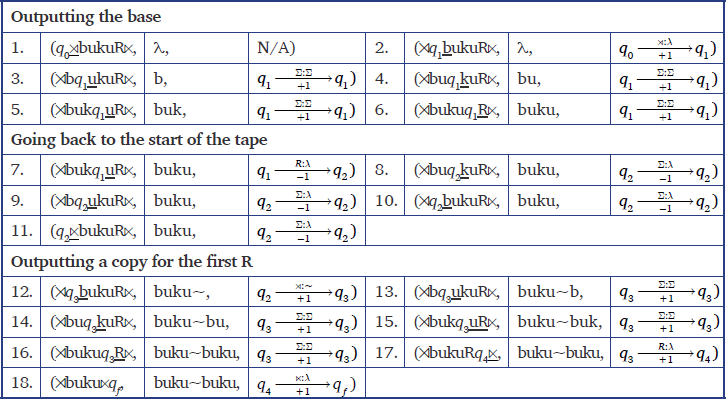
First, consider Figure 5 which is a 2-way FST for doing total reduplication for up to one reduplication instruction R. The way the machine works is that, as we read left to right, if we see a symbol R, then we are told to go back to the start of the input and create a copy. Table 5 illustrates a derivation using this 2-way FST.
The above FST is for reading an input string with exactly one instruction R. If we want to read an input string with one or two instructions, then we need a bigger FST. For example, Figure 6 is a 2-way FST for doing total reduplication for up to two reduplication morphemes.
Informally, if we read the first instruction R, then we go back to the beginning , generate a copy of the input string, and then pass over the first R. If we see a second R, then we again go back to the beginning, generate a new copy of the input string, and then pass over the first two R’s. Table 6 illustrates a derivation using this 2-way FST.
While these 2-way FSTs can sufficiently compute these particular reduplication examples, it is easy to see why allowing any number of input-specified reduplicative instructions is impossible for a regular function. One would either have to have a separate 2-way transducer for each reduplication number, or have one transducer whose state size is equal to the number of possible reduplicative input R morphs. Since this number can be infinite, one would need an infinite number of transducers or a single transducer of infinite size.
The above function is thus not regular, but polyregular. As mentioned, this means the size of the output string grows at a polynomial rate of the input. For example, for an input string wRn of input size |w|+|R| = |w|+n, the output string has a size n|w| where n is not a constant number like 2 for total reduplication or 3 for triplication. It is instead dependent by the number of R morphs in the input. For illustration and space, we only provide a growth-based description of polyregular functions and don’t illustrate with pebble FSTs (though see Bojanczyk (2022) for various descriptions).
Polyregular functions are a well-studied class, and provide a window into logically possible but naturally unattested types of reduplication. For example, one might imagine a type of input-specified copying where the number of reduplicants is based on the length of the input word, i.e. how many segments there are. Given a string w, the process of generating a copy w → w|w| is not a regular function. This is because the number of reduplicants grows polynomially with the length of the input. For example, with an input string ‘abcd’ with a length of 4, the output string contains 4 copies of 4 segments each, for a total of 16 segments. A word with 5 segments would have 25 output segments, and so on, i.e. quadratic growth. Alternately, one might imagine a “partial reduplication” variant of the above where all possible prefixes of a word are copied and concatenated, i.e. for an input word ‘abcd’ the output would be ‘a ab abc abcd’. It is easy to see that this is also properly polyregular.
2.6 Interim summary
The takeaway from this section is that there is a definite upper bound on the generative capacity of individual reduplicative processes.9 Table 7 summarizes the generative capacity of reduplication types. Computationally, attested cases of partial and total reduplication are both regular functions, since they can both be modeled with 2-way FSTs, and partial reduplication is a restricted subclass (rational functions) that can be modeled with 1-way FSTs. Such statuses are constant regardless of the number of generated copies, meaning that triplication and variable numbers of copying are likewise regular.
Generative capacity of reduplication based on number of generated copies for a single semantic feature.
| Input w ∈ Σ* and R ∉ Σ, where u is prefix of w, and n ∈ ℤ+. | |||
| Copying type | Characteristic function | Hypothetical word | Computational class |
| One partial copy (§2.3) | w → uw | patipa→pa∼patipa | Rational function |
| One total copy (§2.2) | w → ww | patipa→patipa∼patipa | Regular function |
| Multiple total copies (§2.4) | w → wwn | patipa→patipa∼patipa∼patipa | Regular function |
| Variable partial copies (§2.4) | w → u+w | patipa→pa(∼pa)*∼patipa | Rational relation |
| Variable total copies (§2.4) | w → ww+ | patipa→patipa (∼patipa)*∼patipa | Regular relation |
| Input-specified copying (§2.5) | wRn → wwn | patipa R R→patipa∼patipa∼patipa | Polyregular function |
| w → w|w| | patipa→patipa (∼patipa)4∼patipa | Polyregular function | |
Logically possible but unattested cases of reduplication inhabit a more expressive but natural extension of regular functions, namely polyregular functions. Studying classes of possible but unattested types of functions is important, because it allows a counterfactual in the presence of limited data. With this counterfactual, we can examine the expressivity of individual theories in a way that is well behaved but not restricted by just attested examples.
With these computational properties in place, the question now is how linguistic theories for reduplication lie with respect to this this regular/polyregular threshold. As we will show, theories which handle reduplication via direct transformations (functions) are regular. In contrast, theories that involve counting the number of reduplicative instructions are not regular but at least polyregular. A compromise between these two extremes of theories exists which is regular.
3 Generative capacity of reduplication theories
There are a large number of theories that have been developed for reduplication. In this section, we use the distinction between regular and polyregular computation to classify different theories. The relevant substantive distinction is based on how the theory determines the number of copies to generate in the output. We find that some theories have the generative capacity of regular functions, while others have the generative capacity of polyregular functions, meaning they treat the phenomenon as a type of computation it is not.
To clarify our narrative, we want to see how a theory operates in its own terms. For those theories which we label as polyregular, they can model regular functions like total reduplication, but they way they do so (their computational behavior) mimics the way a polyregular function operates. Such polyregular theories look ahead to the number of reduplicative instructions R in order to generate the right number of copies, while the regular theories have the number of copies pre-configured in their formulation. If we exploit this ability of the polyregular theories, then we find that polyregular theories can compute polyregular functions like wRn → wwn, while the regular theories cannot.
3.1 Typology of theories of reduplication
Since early seminal work on reduplication (Wilbur 1973; Moravcsik 1978), there have been many generative treatments of reduplication (Marantz 1982; McCarthy & Prince 1986; 1995; Steriade 1988; Raimy & Idsardi 1997; Raimy 2000; Struijke 2000; Inkelas & Zoll 2005; Kiparsky 2010). There are many overviews of developments in reduplication typology and theory (Hurch 2005; Urbanczyk 2007; 2011; Raimy 2011; Inkelas & Downing 2015a; b). Some of the most prominent theories include word-formation rules (Aronoff 1976), templatic reduplication (Marantz 1982), Base-Reduplicant Correspondence theory (BRCT: McCarthy & Prince 1995), and Precedence-Based Phonology (PBP: Raimy 2000).
However, most of these theories are not computationally explicit enough to clearly understand their generative capacity. A minority of theories like PBP do have explicit algorithms (Raimy 1999), and those are computationally very expressive (Dolatian & Raimy forthcoming).
In order to determine the generative capacity of these theories, we do two things. First, as a baseline, we focus on how these theories model the reduplication caused by a single morphosemantic feature (Table 7), not when multiple reduplicative processes are involved in generating a single word.10 Second, as a descriptive device, we classify these different theories of reduplication based on how reduplication is represented in the input: representational vs. non-representational. A theory is representational if it uses special symbols in the input to represent a reduplicative morph. A theory is non-representational if it does not utilize any such representations. We further divide representational theories into counting vs. non-counting theories.
Briefly, theories which create a dependence between the number of reduplicated copies and the number of input reduplicative morphs are not regular, but polyregular. Such theories are reducible to the polyregular input-specified copying functions from §2.5. Such theories explicitly count the number of reduplicative morphs, as a way to count the number of reduplication instructions. In contrast, theories which don’t do counting could be described with a regular function, assuming the theory’s other aspects can be regular too.11 Some of these non-counting are representational (Item-and-Arrangement) while some are not representational (Item-and-Process).
3.2 Non-representational theories can be regular
Non-representational theories include base-copying (Steriade 1988), word-formation rules (Aronoff 1976), and transformational rules (Carrier 1979; Lieber 1980). Here, the input undergoes either a special compounding construction or a readjustment rule. These theories are arguably item-and-process approaches to morphology (cf. Hockett 1942). In these theories, the process itself specifies how many copies to generate, whether one or two. Examples of total reduplication, triplication, and variable reduplication via rules are given below:
- iv.
- Word-formation rules for reduplication
- a.
- Reduplication rule
- X → X∼X
- b.
- Triplication rule
- X → X∼X∼X
- c.
- Variable reduplication rule
- X → X∼X(∼X)*
As explained in §2.4, generating a specific maximally bounded number of copies is regular since the output growth is linearly bounded. This means that if reduplication is implemented via a word-formation rule, then the theory is a regular function. It does not matter if the natural language consists of a large number of word-formation rules, each for generating a different number of copies (reduplication, triplication, quadruplication, etc.). As long as the set of word-formation rules is finite, then the finite union of these rules (and their regular transductions) is regular.
Additionally, for such regular theories, it is not obvious at all how we can create a word-formation rule for an input-specified copying function such as wRn → wwn. This is because such theories by definition don’t allow the input to have representational devices such as R, which would necessarily involve non-linear output growth.
3.3 Counting representational theories cannot be regular
In contrast to non-representational theories, representational theories of reduplication appear to be akin to item-and-arrangement style approaches. Here, the input must have a special symbol which triggers reduplication (see Table 8). Furthermore, based on our computational result, we further divide representational theories into counting-based vs. non-counting-based theories based on whether the input representation ‘counts’ the number of reduplicative morphs.
Classification of theories of reduplication.
| Non-Representational | Representational | |
| Non-counting | Non-counting | Counting |
| Word-formation rule | Variant of BRCT | Variant of BRCT |
| Templates | ||
| Precedence-Based | ||
| Regular | Polyregular | |
Some theories create a 1-to-1 correspondence between the number of reduplicative morphs and the number of copies to generate. This group of ‘counting theories’ include templatic reduplication (Marantz 1982; Kiparsky 2010; Saba Kirchner 2010; 2013; Paschen 2018) and Precedence-Based Phonology (PBP) (Raimy 2000; Papillon 2020). For example, to reduplicate the input kat into kat∼kat, templatic reduplication involves adding an empty prosodic word node in the input. This node is filled out in the output. Similarly, triplication involves adding two empty word nodes.12
- v.
- Templatic reduplication
- /kat + ω / → kat∼kat
- /kat + ω + ω / → kat∼kat∼kat
Computationally, counting theories of reduplication are not regular, but polyregular. The input is examined for the number of reduplicative morphemes/morphs. The number of generated copies will depend on the number of these reduplicative morphs. The size of the output necessarily depends polynomially on the size of the input, and is reducible to the input-specified copying functions in Table 7, meaning it is properly polyregular. For example, we can use template reduplication to model a polyregular function as such as wRn → wwn. The trick is that the prosodic word nodes like ω are our reduplicative instructions R.
PBP is like templatic reduplication in this regard. PBP treats words as graphical structures. It assumes that the input to reduplication contains a special edge making the relation intransitive, a back-loop. These back-loops are reduplicative instructions. To generate triplication, PBP simply adds an additional back-loop as seen below.
- vi.
- Precedence-Based Phonology
- a.
- Input for kat∼kat
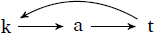
- b.
- Input for kat∼kat∼kat
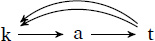
For PBP specifically, Dolatian & Raimy (forthcoming) provide a proof that PBP is not regular. Going beyond their result, we can specifically say that any counting representational theories like PBP are polyregular functions which can be computed with polyregular transducers (Bojańczyk 2018).
As a caveat, it is true that any point in time a natural language will have a finite number of reduplicative processes, such as one construction for total reduplication (wR → ww) and another construction for triplication (wRR → www). If we assume that the language can create only at most some specific number of reduplicative instructions (such as 2), then the language’s reduplication system is regular, though in a way which trivializes the very concept of reduplicative instructions. But, the fact remains that any complete counting-theory of reduplication is supra-regular. This is because the theory is expressive enough to allow the language to innovate and add a new reduplicative construction which uses an extra number of reduplicative instructions (wRn → wwn).
3.4 Non-counting representational theories could be regular
Finally, the third group of theories are representational non-counting theories. This class is much smaller. It only includes some variants of Base-Reduplicant Correspondence Theory (BRCT, McCarthy & Prince 1995).
BRCT is couched within Optimality Theory (OT, Prince & Smolensky 2004) and it is a popular approach. Depending on the exact analysis, BRCT is either a counting or non-counting representational theory. For simple reduplication, the input consists of a string kat and a special symbol Red. The existence of Red triggers segment copying.
- vii
- Base-Reduplicant Correspondence
- a.
- Input for reduplication
- /kat + Red/ → kat∼kat
- b.
- Input for triplication
- i.
- Counting
- /kat + Red + Red/ → kat∼kat∼kat
- ii.
- Non-counting
- /kat + Red2/ → kat∼kat∼kat
Although a BRCT analysis is straightforward for reduplication, to our knowledge there is no explicit BRCT treatment for triplication. In any case, a BRCT-based analysis for triplication could be either counting (vii(b)i) or non-counting (vii(b)ii). A counting analysis would posit two Red morphs for triplication. Here, the two Red symbols do not act as separate morphological constructions; the two symbols act as morphs which constitute a single grammatical construction. This analysis is similar to positing a circumfix as a combination of a prefix and suffix.
Hsiao (2011) sketches out a triplication analysis resembling a counting BRCT treatment. A counting BRCT analysis is polyregular by reduction to the input-specified copying function wRn → wwn. Essentially, such a theory in principle can allow an input with any number of reduplicative morphemes w+Redn.
In contrast, a non-counting BRCT treatment for triplication (vii(b)ii) would posit a single Red symbol. This symbol is diacritically specified to generate two copies, not one. This analysis is suggested in Blevins (1996). A similar analysis is proposed in Zukoff (2017). Based off of a similar analysis by Zuraw (2002), Zukoff (2017) argues that the Red morpheme triggers a constraint Redup which then creates a coupling relationship among multiple copies in the output. His constraint is only exemplified for simple reduplication, but we speculate that it can easily be redefined to allow triplication.
Abstractly, a non-counting representational theory of reduplication is a regular function. The input is examined for the presence of a special symbol Red. The symbol must carry a label that tells the grammar how many copies to generate. A natural language can specify that a morpheme Red1 maps to a single copy, while Red2 maps to two copies. It can specify as many Redx as logically possible. At any given time, the language will have a finite number of Redx morphemes in its lexicon or morphological rules.
In effect, a non-counting version of BRCT is like forcing a regular approximation of a polyregular function. Given a string w and a single reduplicative morph Red, the regular function checks that if that reduplicative morph is actually the reduplicative morph Red1, then it creates the word ww. If that morph is actually Red2, then it creates the word www. At any point in time, the language’s morphology will have a finite set of types of Red morphemes, such as {Red1,Red2,… Redx} for some constant x. Computationally, non-counting BRCT is a regular function that is a union of all possible mappings with these Redx symbols. The result is a big 2-way FST.
- viii.
- Formalization of non-counting BRCT where x is a pre-specified integer like 1, 2, 3, or higher
- w+Red1 → ww
- ∪
- w+Red2 → www
- ∪
- …
- w+Redx → wwx
Although counter-intuitive, such a theory is not polyregular but is regular. This theory cannot do a mapping of wRn to wwn where n is any possible integer. This is because for a specific language for a specific point of time, the function recognizes only a finite number of Red morphemes, not an unbounded number.
4 Polyregular computations for multiple reduplication
The above discussion concerns string languages where the output string contains one or more copies, but the total set of copies is used to mark a single morphosemantic feature. For such processes, the different numbers of copies does not affect the baseline generative capacity of the reduplicative function. Partial reduplication is still rational, and total reduplication is still regular, regardless of the number of copies. We discuss rarer cases where multiple reduplicants are present within the same word. Analysis of their computation is much less clear. The computation depends on whether there is a bound on how many copies are created, and whether the computation is treated as a single function or an (unbounded) sequence of functions.13
4.1 Computational vagueness of multiple reduplication
When a word contains multiple reduplicated copies, it’s common to find that the different copies belong to separate reduplicative processes. For example, a word can have multiple partial copies that designate different semantic features (Urbanczyk 1999; 2001; Fitzpatrick & Nevins 2004; Fitzpatrick 2006; Stonham 2007; Zimmermann 2021; Mellesmoen & Urbanczyk 2021). As long as the number of such partial reduplicants is bound, then the function is regular (in fact, rational).
Multiple reduplication is also found in total reduplication in Guébie (Sande 2017; 2021). One type of total reduplication is used to mark reciprocalization, abstractly as w → ww. A separate total reduplication process is used for nominalization, abstractly as w → ww. Each of these functions on their own is regular. When nominalization applies to the output of reciprocalization, we generate in total four copies: w → ww → wwww. The composition of these two regular functions is thus another regular function.
Much rarer are languages where the output can contain multiple copies such that each copy expresses the same semantic feature (called re-triplication in Friday-Otun 2021). For example in Tigre (Table 9), the syllable of the penultimate root consonant is reduplicated (underlined) to mark frequentativity (Rose 1997; 2003a; b). This partial reduplication can apply multiple times, with each generated copying adding an additional semantic level of frequency or attenuation.
Multiple partial reduplication in Tigre.
| dəgm-a: | ‘tell, relate’ |
| dəga:gəm-a: | ‘tell stories occasionally’ |
| dəga:ga:gəm-a: | ‘tell stories very occasionally’ |
| dəga:ga:ga:gəm-a: | ‘tell stories infrequently’ |
In terms of a function, we can conceptualize the generation of the output with four copies dəga:ga:ga:gəm-a: in one of two ways: factorized (cyclic) and unfactorized (non-cyclic). The factorized approach would iteratively apply the same partial reduplication function fcv four times, with each function fcv adding a copy: dəgm-a: → dəga:gəm-a: → dəga:ga:gəm-a: → dəga:ga:ga:gəm-a:. The unfactorized approach is to generate the four copies in one single swoop as a single function f4 which is specified to generate four copies: dəgm-a: → dəga:ga:ga:gəm-a:. Because this is partial reduplication and because the maximum number of copies is 4 (Rose 2003b: 124), both functions fcv and f4 would be rational functions.14
The Tigre example focuses on how the same feature F and its reduplicant can be repeated to add semantic nuances. The reduplicative pattern in Tigre is partial. There are other rare cases of natural language where the repeated reduplicative process is total reduplication. For example in Runyankore (Hyman 2020), frequentativity is marked by total reduplication of the root, abstractly as w → ww ‘to w a lot’. The root can reduplicate further and further to designate greater degrees of frequentativity: www*. The individual copies be segmentally identical or undergo some truncation. Each application of reduplication is regular. Besides Runyankore, another possible case is English contrastive reduplication (Ghomeshi et al. 2004).
For Runyankore, the computation depends on if a theory uses cyclicity, bounds on the number of copies, and how it represents the semantically-based input to reduplication. If factorized with cycles of the same function, then each cycle of a function would be regular. If we try to use a single collapsed function, then the computational expressivity depends on how many times a copy can be generated. If such a bound on the number of copies exists, then the finite composition of multiple total reduplication functions would be a single regular function. But if there is no bound, then regularity would depend on how the input string w looks like and how the mapping between semantic features F to the input works. If the input it treated as a word plus a sequence of identical frequentative features F, then this process is reduced to the polyregular input-specified copying: w Fn → wwn.
In sum, for repeated but bounded application of a reduplicative process, this process is rational for generating partial copies, regular for total copies. However, if there is no bound on the number of total copies, then we may be entering polyregular computation. The mathematical perspective shows that any answer to this question depends on a unified theory of how repeated reduplication is modeled in the input to the morphophonological derivation, meaning it should be a key focus of future research in reduplication.
4.2 Understanding the role of polyregularity
So far, we discussed how individual theories of reduplication are regular or polyregular. Individual reduplicative functions are regular, while the interaction among an unbounded number of reduplication functions might not be regular. Given this state of affairs, one can ask: Do regular theories then undergenerate, and do we now need polyregular theories The answer is somewhere between ‘no’ and ‘unclear’.
The main problem behind multiple reduplication is how we encode concepts like cyclicity and semantic features, and how composition can be integrated into our formal model of reduplication.
For the Guébie data, the two total reduplication functions are individually regular. The composition of a bounded, finite sequence of regular functions is at most regular. Thus the composition of these two regular reduplicative processes is thus also regular. Thus a regular theory can model the data.
But now consider Runyankore. Total reduplication on its own is still regular. But the language allows the unbounded application of the same regular function. But the composition of an unbounded sequence can be non-regular. In order to handle the data, we need to be more exact about how the morphology-phonology interface is formalized. One option is to combine a regular theory of reduplication (like word-formation rules) with cyclicity: w → ww → www → … → wwn. Another option is to combine a polyregular theory with a semantically-enriched input representation: w+Fn → wwn.
The choice between the two approaches cannot be settled based on just the empirical data behind reduplication. Instead, the choice is up to the analyst on how they conceptualize the morphology-phonology interface: with cyclicity or with semantically-enriched inputs?
5 Discussion
Having established the kinds of computation different theories must invoke, this section goes over larger takeaways from our paper. These results were focused on how reduplicative structures are generated. This task is computationally simpler than the task of recognizing reduplicative structure (§5.1). As for linguistic theory, this result highlights the problem of formal implicitness in reduplication, which does affect the computation (§5.2). Some polyregular models could potentially get reduced to regular computation by not incorporating tier conflation (§5.3). Finally, at least some theories of reduplication resist a simple formalization, such as Morphological Doubling Theory (§5.4). All of this is evidence that there is computational significance to how one represents or derive reduplicative structures.
5.1 String membership vs. string transformation
One takeaway from this and related work (Dolatian & Heinz 2020; Wang 2021a) is that making copies is computationally simpler than recognizing copies. Computational perspectives on reduplication, and copying more generally, have centered around the complexity of the “copy language”, which is the set of totally reduplicated strings: {ww | w ∈ Σ*}, which is not a regular language since there is no bound on the reduplicant size (Culy 1985), nor is it a context-free language for the same reason. Instead, more advanced types of acceptors are needed, such as context-sensitive grammars (Seki et al. 1991; Albro 2000; 2005; Stabler 2004; Clark & Yoshinaka 2014), a combination of an FSA with some queue mechanism (Gazdar & Pullum 1985; Wang 2021a; b), or other elaborate extensions (Manaster-Ramer 1986; Savitch 1989). However, when viewed as a transformation f(w) = ww, this copying function is a regular function.
If we step back and take a broader perspective, it is useful to compare what we know about functions which map strings to strings with what we know about functions which map real numbers to real numbers. The latter has been informed by hundreds of years of mathematical study and we are quite conversant in different classes of functions over the reals (linear, polynomial, trigonometric, logarithmic, etc.) and many of the properties of such functions. However, our knowledge of functions over strings is still, relatively speaking, in an early stage. It is our view that it behooves us – especially for those with a goal to better understand natural language – to better understand the different kinds of string-to-string functions and their properties. This paper takes a small step in that direction.
5.2 Refining reduplicative theories
One possible hypothesis from this paper is that, because reduplication on its own is computationally regular, then psychologically real models of reduplication should likewise be computationally regular. We are agnostic over this hypothesis, but we discuss it.
This hypothesis is a significant issue for BRCT. As explained, proposals on reduplication in BRCT are not specified enough to make a final determination of their computational power. There is wiggle room over whether the Red symbol acts as a single diacritic for reduplication processes (thus being regular) or as a sequence of instructions for each copy (thus being polyregular). This choice will fundamentally affect the models. The regular approach can be considered an Item-and-Process formulation. Such a formulation seems unlikely to be developed within BRCT because of the dependence on correspondence theory to compute the content of the Red morph. If the evaluation of the Red morph becomes a process, then either all of correspondence theory becomes a process or reduplication as a phenomenon is removed from phonology. Triplication as a phenomenon also lacks an explicit analysis in BRCT models. We are unaware of any active research on these topics.
As for templatic reduplication, all current models (McCarthy et al. 2012; Zimmermann 2013) are Item-and-Arrangement models that inherit the basic architecture from Marantz (1982). Empty prosodic structure is added and then filled by copying melodic structure. They would all still require polyregular computation. Again, there is an alternative possibility that reduplication is a process that is diacritically triggered by these empty nodes. But then this process alternative would nullify the main thrust of this line of research.
5.3 Tier conflation
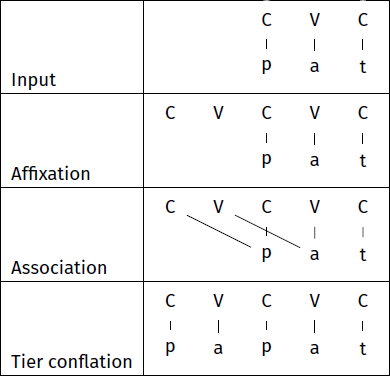
For the representational counting theories like PBP or templatic copying, the entire computation is polyregular. However, within the literature, these theories do consist of multiple derivational stages. To illustrate, consider a hypothetical example of initial-CV reduplication: pat→pa∼pat in Table 10. Assume a templatic approach to reduplication (Marantz 1982).
The input contains the segments connected to CV-timing slots. A reduplicative CV template is affixed; this template acts as the reduplicative instruction. The CV template is associated with the initial segments. This creates multiple crossing corresponding relations. In the last stage, these crossing relations are removed by copying the segments. This second stage has been called tier conflation (McCarthy 1986; Mester 1986; McCarthy & Prince 1995) for the templatic copying theories, and serialization or linearization for PBP (Raimy 1999).
Over string-to-string functions, this second stage of tier conflation is necessary in order to generate a string. Without tier conflation, there would not be a copying process at all. It is an open question if the polyregular computation can be avoided if these representational theories were instead treated as graph-to-graph functions, without any tier conflation.
This option without tier-conflation is an interesting option for PBP. As explained before, PBP uses graphical structures. It proposes that precedence structure in phonology is a directed graph with reduplication being a case that demonstrates that graphs in human language can have cycles. Papillon (2020) elaborates the possible graphs that would be involved in phonology and morphology. With tier conflation, converting these graphs is not MSO-definable (Dolatian & Raimy forthcoming). But alternatively without tier conflation, processing these graphical structures is similar to topological sorting (Höpfner 2011) with parallel edges and cycles (Papillon 2020; 2021), as opposed to using paths (Idsardi & Raimy 2013).
5.4 Morphological Doubling Theory
This paper tried to survey common or previously common approaches in modeling reduplication. We tried to catalog as many theories as we could in terms of whether the theory uses regular or polyregular computation. One theory that we haven’t discussed yet is Morphological Doubling Theory (MDT) (Inkelas & Zoll 2005). Unfortunately, current formulations of the theory are too vague to computationally formalize.
The main idea behind MDT is that reduplication is not a transformation like w+Red → ww. Instead, reduplication is about creating a compound of two strings, such that the two strings are identical (total reduplication) or near-identical (partial reduplication). For our computational purposes, the problem with this approach is that it reduces reduplication to recognizing a string language, and not a string-to-string function or transformation.
In our reading of Inkelas & Zoll (2005), we couldn’t find unambiguous examples of how MDT would model the transformation from an unreduplicated string w to a reduplicated string ww. The theory instead implies that the lexicon or the morphology of a natural language has something like a template or construction whereby words like ww are licit and have a specific semantic interpretation when compared to w. From this reading, MDT is not a theory about string-to-string mappings, but of string languages.15 This implicitness about MDT has been somewhat noticed in the previous literature (cf. Raimy 2006: 484ff). Thus, we a priori cannot apply concepts like ‘regular functions’ or ‘polyregular functions’ to MDT in the way that we did for others, simply because MDT is not defined as a transformation in the first place. Until such a theory is created, we cannot computationally compare MDT against the other theories, only against the prior work on reduplication as a language, as overviewed in §5.1.
5.5 Repetition in cognition
The formalization of reduplication theories raises the issue of how theories represent the idea of not only copying segments, but also the sequencing of repeated segments within a reduplicative construction. These issues have analogs to the role of sequencing and repetition in cognition (Endress et al. 2007; Moreton et al. 2021).
Cognitive neuroscience has provided evidence for the role that the hippocampus plays in navigation and episodic memory (Hasselmo 1999). Buzsáki & Tingley (2018) argue that the hippocampus is a generalized sequence generator. Words (or more properly morphemes) can be conceived of as sequences of phonological categories, thus some questions and findings from cognitive neuroscience can be relevant to our investigation of the nature of reduplication. Hasselmo (2011) identifies the question of how to deal with forks in overlapping sequences through activation levels associated with goal states. Hasselmo (2011) addresses loops in paths by proposing arc length cells that distinguish between the length of a sequence with or without the loop part. Analogously, these arc length cells (or the time cell equivalent: MacDonald & Tonegawa (2021)) would act as a counter for our polyregular models of reduplication. Coded trajectories in the hippocampus are more graph-like than string-like, and consequently further investigation into graph-to-graph functions seems warranted.
An interesting possibility is that reduplication is special when compared to morphology and phonology because it reflects the use of cognition-general mechanisms for sequences. Endress et al. (2007) argues that learning repeated sequences (i.e. reduplication) is different from learning ordinal sequences in an artificial grammar. If the hippocampus provides the general mechanism for sequences (Buzsáki & Tingley 2018) then recognizing and learning repetition could be a fundamental cognitive function and then learning additional relations among sequences, such as the ratios among notes in the Endress et al. (2007) study, is based on an additional elaborated learning mechanism.
6 Conclusion
This paper synthesized the different strands of work on the computation, mathematics, and theories of reduplication. Although reduplication is more powerful or expressive than the rest of morphology and phonology, we can better understand its generative capacity in terms of string-to-string functions. Specifically, unbounded fixed-n copying (f(w) = wn) is a regular function, but unbounded input-specified copying (f(wRn) = wwn) is a polyregular function.
We then surveyed reduplicative theories and found that many of them are polyregular. These theories need to count the number of reduplicative instructions in the input in order to determine how many copies to generate, exemplified by broader types of reduplication like triplication. Depending on the theory, these instructions can be graph-based loops, empty prosodic nodes, a string of Red morphs, among others.
In contrast, some theories treat reduplication as a function where the number of copies is pre-determined. This tends to be the case in theories which adopt word-formation rules and which view morphology in terms of “item-as-process” as opposed to “item-and-arrangement.” Interestingly, we also found that Base-Reduplicant Correspondence Theory is insufficiently well-defined to determine whether it is unambiguously polyregular or not. Some phonologists imply that it is and others imply that it is not.
Notes
- Table 1 cites order-preservation as a difference between rational and regular functions. We don’t discuss the difference between these two function classes in depth. See Dolatian et al. (2021) for discussion on some of these formal parameters. [^]
- There are many 1-way FST approximations of total reduplication (Walther 2000; Beesley & Karttunen 2000; 2003; Cohen-Sygal & Wintner 2006; Hulden & Bischoff 2009; Hulden 2009). However, these approximations are generally inadequate (Roark & Sproat 2007: 54). See Dolatian & Heinz (2020) for an overview. [^]
- They are called rational because they can be alternatively defined by the more general and classical notion of rational subsets of monoids. Kaplan & Kay (1994) depart from convention by calling the functions generated by 1-way FSTs as ‘regular functions.’ [^]
- While the weak generative capacity (the input-output pairs) of any partial reduplication type is sufficiently described by rational functions, the strong generative capacity (how the computation is carried out) of a 1-way FST does not necessarily match the intuition behind copying, that is, that the same element in the input has corresponding outputs in the output base and reduplicant. This is apparent in the 2-way and 1-way transducers encoding partial reduplication processes in Figure 2 and Figure 3, without vs. with memorization. For this reason it has been argued that the computational nature of partial reduplication is actually Regular, since the derivations more closely match the derivations given by 2-way transducers (Dolatian et al. 2021). [^]
- The above concerns where a single semantic feature is marked by triplicating a base word, schematically w → www. We call this ‘triplication’. However, some grammars or sources use the term ‘triplication’ is a looser way to mean whenever 3 copies of a base are found (Harrison 1973; Blust 2001; Smith 2016; Gates 2017; Terfa 2020) (see more in Austronesian: Blust 2013: ch6.11). For example, some w is reduplicated to mark some feature F1 w → ww, and this output is then the input to another reduplication function for a feature F2 ww → www, though F1 and F2 might be the same feature under some semantic analyses. We categorize these latter cases not as triplication but as multiple reduplication in §4; other labels that we’ve come across are ‘serial reduplication’ or ‘recursive reduplication’. [^]
- This is an informal restriction. For example, if the function copies consonant-initial words 2 times, while vowel-initial words 3 times, that is still regular. The trick is that the number of unboundedly-sized copies is decided before examining the entire input, and without recursively copying the previously generated copies. [^]
- The automata characterization makes it easy to see why regular functions are a special case of polyregular functions. They are the pebble transducers that have exactly 1 pebble, i.e. the read head, meaning the growth is at most (n1), i.e. linear. [^]
- One may think of these as pseudo-counting because this function does not necessarily need to have counting powers. It could recursively generate an output copy as it processes each instruction. For this function, the base case would be f(wR0) = w and the recursive case is f(wRn) = f(wRn-1)w. This means that the regular case of copying a bounded number of times n is simply input-specified copying with one argument saturated (n). So the regular function is an ‘instance’ of the polyregular function. This is related to the notion of currying functions. [^]
- We add the qualifier ‘individual’ because more data is needed to determine the generative capacity of attested natural languages with the unbounded application of reduplication. For example, if a reduplicative process can apply an unbounded number of times on itself, does it ever go into polyregular computation? Data is too limited to know. [^]
- When modeling multiple reduplicative reduplicative processes or iterated reduplication, the computation would likely need some sort of cyclic mechanism. Cyclic computation is however a Pandora’s Box for the computational linguist because we cannot guarantee that the composition of an infinite number of regular functions is a single regular function. See discussion in §4. [^]
- A non-counting theory might not be regular for other reasons, such as if the theory is couched in OT which is generally not finite-state definable (Hao 2019; Lamont 2021). [^]
- To illustrate, to model triplication and quadruplication in Chinese languages, Chiang (1994) uses empty syllable nodes. They use syllable nodes instead of word nodes because Chinese languages have a strong tendency to be monosyllabic. [^]
- We thank Larry Hyman and Andrew Lamont for discussion on this data. [^]
- We can replace f4 with a function fcv that just reduplicates the penultimate root consonant. To generate four copies, the input would be enriched with a sequence of features F to mark each reduplicant: /dəgm-a: + F+F+F/ → dəga:ga:ga:gəm-a:. This function is rational because we would just memorize the penultimate root and output one copy of it per F. [^]
- Such a string language for MDT would not be a regular language (cf. footnote 5.1). [^]
Funding Information
Eric Raimy is supported by the Marjorie and Lorin Tiefenthaler Chair in English
Competing interests
The authors have no competing interests to declare.
References
Albro, Daniel M. 2000. Taking Primitive Optimality Theory beyond the finite state. In Eisner, Jason & Karttunen, Lauri & Thériault, Alain (eds.), Finite-state phonology: Proceedings of the 5th workshop of SIGPHON, 57–67. Luxembourg.
Albro, Daniel M. 2005. Studies in computational Optimality Theory, with special reference to the phonological system of Malagasy. Los Angeles: University of California, Los Angeles dissertation.
Aronoff, Mark. 1976. Word formation in generative grammar (Linguistic Inquiry Monographs 1). Cambridge, MA: The MIT Press.
Beesley, Kenneth & Karttunen, Lauri. 2000. Finite-state non-concatenative morphotactics. In Proceedings of the 38th Annual Meeting on Association for Computational Linguistics (ACL ’00), 191–198. Hong Kong: Association for Computational Linguistics. DOI: http://doi.org/10.3115/1075218.1075243
Beesley, Kenneth & Karttunen, Lauri. 2003. Finite-state morphology: Xerox tools and techniques. Stanford, CA: CSLI Publications.
Beguš, Gašper. 2021. Identity-Based Patterns in Deep Convolutional Networks: Generative Adversarial Phonology and Reduplication. Transactions of the Association for Computational Linguistics 9. 1180–1196. DOI: http://doi.org/10.1162/tacl_a_00421
Blevins, Juliette. 1996. Mokilese reduplication. Linguistic Inquiry 27(3). 523–530. https://www.jstor.org/stable/4178949. DOI: http://doi.org/10.2307/3623444
Blust, Robert. 2001. Thao triplication. Oceanic Linguistics 40(2). 324–335. http://doi.org/10.2307/3623444
Blust, Robert. 2013. The Austronesian languages (Asia-Pacific Open-Access Monographs). Canberra: Asia-Pacific Linguistics. http://hdl.handle.net/1885/10191
Bojańczyk, Mikołaj. 2018. Polyregular functions. ArXiv preprint. https://arxiv.org/abs/1810.08760.
Bojańczyk, Mikołaj & Kiefer, Sandra & Lhote, Nathan. 2019. String-to-string interpretations with polynomial-size output. In Baier, Christel & Chatzigiannakis, Ioannis & Flocchini, Paola & Leonardi, Stefano (eds.), 46th international colloquium on automata, languages, and programming, icalp 2019, july 9–12, patras, greece. (lipics), vol. 132. 106:1–106:14. Schloss Dagstuhl – Leibniz-Zentrum fuer Informatik. http://doi.org/10.4230/LIPIcs.ICALP.2019.106
Bojanczyk, Mikolaj. 2022. Transducers of polynomial growth. In Proceedings of the 37th annual acm/ieee symposium on logic in computer science, 1–27. DOI: http://doi.org/10.1145/3531130.3533326
Buzsáki, György & Tingley, David. 2018. Space and time: The hippocampus as a sequence generator. Trends in cognitive sciences 22(10). 853–869. DOI: http://doi.org/10.1016/j.tics.2018.07.006
Carrier, Jill Louise. 1979. The interaction of morphological and phonological rules in Tagalog: a study in the relationship between rule components in grammar: Massachusetts Institute of Technology dissertation. http://hdl.handle.net/1721.1/16199.
Chandlee, Jane. 2014. Strictly local phonological processes. Newark, DE: University of Delaware dissertation.
Chandlee, Jane. 2017. Computational locality in morphological maps. Morphology 27(4). 1–43. DOI: http://doi.org/10.1007/s11525-017-9316-9
Chandlee, Jane & Heinz, Jeffrey. 2012. Bounded copying is subsequential: Implications for metathesis and reduplication. In Proceedings of the 12th Meeting of the ACL Special Interest Group on Computational Morphology and Phonology (SIGMORPHON’12), 42–51. Montreal, Canada: Association for Computational Linguistics.
Chandlee, Jane & Heinz, Jeffrey. 2018. Strict locality and phonological maps. Linguistic Inquiry 49(1). 23–60. DOI: http://doi.org/10.1162/LING_a_00265
Chandlee, Jane & Heinz, Jeffrey & Jardine, Adam. 2018. Input strictly local opaque maps. Phonology 35(2). 171–205. DOI: http://doi.org/10.1017/S0952675718000027
Chiang, Wen-yu. 1994. The prosodic morphology and phonology of affixation in Taiwanese and other Chinese languages. Newark, DE: University of Delaware dissertation.
Clark, Alexander & Yoshinaka, Ryo. 2014. Distributional learning of parallel multiple context-free grammars. Machine Learning 96(1–2). 5–31. DOI: http://doi.org/10.1007/s10994-013-5403-2
Cohen-Sygal, Yael & Wintner, Shuly. 2006. Finite-state registered automata for nonconcatenative morphology. Computational Linguistics 32(1). 49–82. DOI: http://doi.org/10.1162/coli.2006.32.1.49
Cohn, Abigail C. 1989. Stress in Indonesian and bracketing paradoxes. Natural language & linguistic theory 7(2). 167–216. DOI: http://doi.org/10.1007/BF00138076
Culy, Christopher. 1985. The complexity of the vocabulary of Bambara. Linguistics and Philosophy 8. 345–351. DOI: http://doi.org/10.1007/BF00630918
Dolatian, Hossep & Heinz, Jeffrey. 2018a. Learning reduplication with 2-way finitestate transducers. In Unold, Olgierd & Dyrka, Witold & Wieczorek, Wojciech (eds.), Proceedings of machine learning research: International Conference on Grammatical Inference, vol. 93 (Proceedings of Machine Learning Research), 67–80. Wroclaw, Poland. DOI: http://doi.org/10.18653/v1/W18-5807
Dolatian, Hossep & Heinz, Jeffrey. 2018b. Modeling reduplication with 2-way finitestate transducers. In Proceedings of the 15th SIGMORPHON Workshop on Computational Research in Phonetics, Phonology, and Morphology. Brussells, Belgium: Association for Computational Linguistics. DOI: http://doi.org/10.18653/v1/W18-5807
Dolatian, Hossep & Heinz, Jeffrey. 2020. Computing and classifying reduplication with 2-way finite-state transducers. Journal of Language Modeling 8. 79–250. DOI: http://doi.org/10.15398/jlm.v8i1.245
Dolatian, Hossep & Raimy, Eric. forthcoming. Evaluating precedence-based phonology: Logical structure of reduplication and linearization. In Dolatian, Hossep & Heinz, Jeffrey & Strother-Garcia, Kristina (eds.), Doing computational phonology. Oxford: Oxford University Press. https://lingbuzz.net/lingbuzz/005600.
Dolatian, Hossep & Rawski, Jonathan & Heinz, Jeffrey. 2021. Strong generative capacity of morphological processes. In Proceedings of the Society for Computation in Linguistics, vol. 4. 228–243. http://doi.org/10.7275/sckf-8f46
Endress, Ansgar D. & Dehaene-Lambertz, Ghislaine & Mehler, Jacques. 2007. Perceptual constraints and the learnability of simple grammars. Cognition 105(3). 577–614. DOI: http://doi.org/10.1016/j.cognition.2006.12.014
Engelfriet, Joost & Hoogeboom, Hendrik Jan. 2001. MSO definable string transductions and two-way finite-state transducers. Transactions of the Association for Computational Linguistics 2(2). 216–254. DOI: http://doi.org/10.1145/371316.371512
Filiot, Emmanuel & Reynier, Pierre-Alain. 2016. Transducers, logic and algebra for functions of finite words. ACM SIGLOG News 3(3). 4–19. DOI: http://doi.org/10.1145/2984450.2984453
Fitzpatrick, Justin. 2006. Sources of multiple reduplication in Salish and beyond. In Bischoff, Shannon T. & Butler, Lynnika & Norquest, Peter & Siddiqi, Daniel (eds.), MIT working papers on endangered and less familiar languages: Studies in salishan 7, 211–240.
Fitzpatrick, Justin & Nevins, Andrew. 2004. Linearizing nested and overlapping precedence in multiple reduplication. In University of Pennsylvania Working Papers in Linguistics, 75–88. https://repository.upenn.edu/pwpl/vol10/iss1/7.
Friday-Otun, Joseph Omoniyi. 2021. The study of reduplication and retriplication in the Yoruba language. Journal of Language and Literature 21(1). 198–211. DOI: http://doi.org/10.24071/joll.v21i1.2933
Gates, Jesse P. 2017. Verbal triplication morphology in Stau (Mazi dialect). Transactions of the Philological Society 115(1). 14–26. DOI: http://doi.org/10.1111/1467-968X.12083
Gazdar, Gerald & Pullum, Geoffrey K. 1985. Computationally relevant properties of natural languages and their grammars. New generation computing 3. 273–306. DOI: http://doi.org/10.1007/BF03037123
Ghomeshi, Jila & Jackendoff, Ray & Rosen, Nicole & Russell, Kevin. 2004. Contrastive focus reduplication in English (the salad-salad paper). Natural Language & Linguistic Theory 22(2). 307–357. DOI: http://doi.org/10.1023/B:NALA.0000015789.98638.f9
Hao, Yiding. 2019. Finite-state optimality theory: non-rationality of harmonic serialism. Journal of Language Modelling 7(2). 49–99. DOI: http://doi.org/10.15398/jlm.v7i2.210
Harrison, Sheldon P. 1973. Reduplication in micronesian languages. Oceanic Linguistics 12(1/2). 407–454. DOI: http://doi.org/10.2307/3622862
Hasselmo, Michael E. 1999. Neuromodulation and the hippocampus: memory function and dysfunction in a network simulation. Progress in Brain Research 121. 3–18. DOI: http://doi.org/10.1016/S0079-6123(08)63064-2
Hasselmo, Michael E. 2011. How we remember: Brain mechanisms of episodic memory. Cambridge, USA: MIT press. DOI: http://doi.org/10.7551/mitpress/9780262016353.001.0001
Heinz, Jeffrey & Idsardi, William. 2013. What complexity differences reveal about domains in language. Topics in Cognitive Science 5(1). 111–131. DOI: http://doi.org/10.1111/tops.12000
Hockett, Charles F. 1942. A system of descriptive phonology. Language 18. 3–21. DOI: http://doi.org/10.2307/409073
Hopcroft, John E & Ullman, Jeffrey D. 1969. Formal languages and their relation to automata. Boston, MA: Addison-Wesley Longman Publishing Co., Inc. https://dl.acm.org/doi/book/10.5555/1096945.
Höpfner, Hagen. 2011. Topological sorting-how should i begin to complete my to do list? In Vöcking, Berthold & Alt, Helmut & Dietzfelbinger, Martin & Reischuk, Rüdiger & Scheideler, Christian & Vollmer, Heribert & Wagner, Dorothea (eds.), Algorithms unplugged, 39–45. Heidelberg: Springer. DOI: http://doi.org/10.1007/978-3-642-15328-0_5
Hsiao, Yuchau E. 2011. Cross-anchoring of tones in Hoiliuk triplication. In Proceedings of the 23rd north american conference on chinese linguistics, vol. 2. 151–163. University of Oregon Eugene, OR. http://nccur.lib.nccu.edu.tw/handle/140.119/72380.
Hulden, Mans. 2009. Finite-state machine construction methods and algorithms for phonology and morphology. University of Arizona dissertation.
Hulden, Mans & Bischoff, Shannon T. 2009. A simple formalism for capturing reduplication in finite-state morphology. In Piskorski, Jakub & Watson, Bruce & Yli-Jyrä, Anssi (eds.), Proceedings of the 2009 Conference on Finite-State Methods and Natural Language Processing: Post-proceedings of the 7th International Workshop FSMNLP 2008, 207–214. Amsterdam: IOS Press.
Hurch, Bernhard (ed.). 2005. Studies on reduplication (Empirical Approaches to Language Typology 28). Berlin: Walter de Gruyter. DOI: http://doi.org/10.1515/9783110911466
Hyman, Larry. 2020. Tone in Runyankore verb stem reduplication. Stellenbosch Papers in Linguistics Plus 62. 51–80. DOI: http://doi.org/10.5842/62-2-901
Idsardi, William & Raimy, Eric. 2013. Three types of linearization and the temporal aspects of speech. In Biberauer, Theresa & Roberts, Ian (eds.), Challenges to linearization, 31–56. Mouton de Gruyter, Berlin. DOI: http://doi.org/10.1515/9781614512431.31
Inkelas, Sharon & Downing, Laura J. 2015a. What is reduplication? Typology and analysis part 1/2: The typology of reduplication. Language and Linguistics Compass 9(12). 502–515. DOI: http://doi.org/10.1111/lnc3.12166
Inkelas, Sharon & Downing, Laura J. 2015b. What is reduplication? Typology and analysis part 2/2: The analysis of reduplication. Language and Linguistics Compass 9(12). 516–528. DOI: http://doi.org/10.1111/lnc3.12152
Inkelas, Sharon & Zoll, Cheryl. 2005. Reduplication: Doubling in morphology. Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/CBO9780511627712
Johnson, C Douglas. 1972. Formal aspects of phonological description. The Hague: Mouton. DOI: http://doi.org/10.1515/9783110876000
Kaplan, Ronald M & Kay, Martin. 1994. Regular models of phonological rule systems. Computational linguistics 20(3). 331–378.
Kiparsky, Paul. 2010. Reduplication in stratal OT. In Uyechi, Linda Ann & Wee, Lian-Hee (eds.), Reality exploration and discovery: Pattern interaction in language & life, 125–142. Stanford: CSLI Press. https://web.stanford.edu/~kiparsky/Papers/reduplication.pdf.
Koskenniemi, Kimmo. 1983. Two-level morphology: A general computational model for word-form recognition and production. University of Helsinki dissertation. DOI: http://doi.org/10.3115/980431.980529
Lamont, Andrew. 2021. Optimizing over subsequences generates context-sensitive languages. Transactions of the Association for Computational Linguistics 9. 528–537. DOI: http://doi.org/10.1162/tacl_a_00382
Lhote, Nathan. 2020. Pebble minimization of polyregular functions. In Proceedings of the 35th annual acm/ieee symposium on logic in computer science, 703–712. DOI: http://doi.org/10.1145/3373718.3394804
Lieber, Rochelle. 1980. On the organization of the lexicon. Massachusetts Institute of Technology dissertation.
MacDonald, Christopher J. & Tonegawa, Susumu. 2021. Crucial role for CA2 inputs in the sequential organization of CA1 time cells supporting memory. Proceedings of the National Academy of Sciences 118(3). DOI: http://doi.org/10.1073/pnas.2020698118
Manaster-Ramer, Alexis. 1986. Copying in natural languages, context-freeness, and queue grammars. In Proceedings of the 24th Annual Meeting on Association for Computational Linguistics, 85–89. Association for Computational Linguistics. DOI: http://doi.org/10.3115/981131.981145
Marantz, Alec. 1982. Re reduplication. Linguistic Inquiry 13(3). 435–482. https://www.jstor.org/stable/4178287. DOI: http://doi.org/10.1007/s11525-012-9203-3
McCarthy, John J. 1986. OCP effects: Gemination and antigemination. Linguistic Inquiry 17(2). 207–263.
McCarthy, John J. & Kimper, Wendell & Mullin, Kevin. 2012. Reduplication in Harmonic Serialism. Morphology 22(2). 173–232. http://doi.org/10.1007/s11525-012-9203-3
McCarthy, John J. & Prince, Alan. 1986. Prosodic morphology. Unpublished manuscript.
McCarthy, John J. & Prince, Alan. 1995. Faithfulness and reduplicative identity. In Beckman, Jill N. & Dickey, Laura Walsh & Urbanczyk, Suzanne (eds.), Papers in optimality theory. Amherst, MA: Graduate Linguistic Student Association, University of Massachusetts.
Mellesmoen, Gloria & Urbanczyk, Suzanne. 2021. Binarity in prosodic morphology and elsewhere. In Proceedings of the Annual Meetings on Phonology, vol. 9. DOI: http://doi.org/10.3765/amp.v9i0.4924
Mester, R. Armin. 1986. Studies in tier structure. Amherst, MA: University of Massachusetts, Amherst dissertation. https://scholarworks.umass.edu/dissertations/AAI8701200.
Moravcsik, Edith. 1978. Reduplicative constructions. In Greenberg, Joseph (ed.), Universals of human language, vol. 1, 297–334. Stanford, California: Stanford University Press.
Moreton, Elliott & Prickett, Brandon & Pertsova, Katya & Fennell, Josh & Pater, Joe & Sanders, Lisa. 2021. Learning repetition, but not syllable reversal. In Proceedings of the Annual Meetings on Phonology, vol. 9. DOI: http://doi.org/10.3765/amp.v9i0.4912
Nelson, Max & Dolatian, Hossep & Rawski, Jonathan & Prickett, Brandon. 2020. Probing RNN encoder-decoder generalization of subregular functions using reduplication. In Proceedings of the Society for Computation in Linguistics, vol. 3. DOI: http://doi.org/10.7275/xd0r-pg04
Papillon, Maxime. 2020. Precedence and the lack thereof: Precedence-relation-oriented phonology: University of Maryland dissertation. http://hdl.handle.net/1903/26391.
Papillon, Maxime. 2021. The match-extend serialization algorithm in multiprecedence. In Proceedings of the 18th SIGMORPHON Workshop on Computational Research in Phonetics, Phonology, and Morphology, 23–31. Online: Association for Computational Linguistics. https://aclanthology.org/2021.sigmorphon-1.3. DOI: http://doi.org/10.18653/v1/2021.sigmorphon-1.3
Paschen, Ludger. 2018. The interaction of reduplication and segmental mutation: A phonological account. Universität Leipzig dissertation.
Pfau, Roland & Steinbach, Markus. 2006. Pluralization in sign and in speech: A crossmodal typological study. Linguistic Typology 10(2). 135–182. DOI: http://doi.org/10.1515/LINGTY.2006.006
Prickett, Brandon & Traylor, Aaron & Pater, Joe. 2022. Learning reduplication with a neural network that lacks explicit variables. Journal of Language Modelling 10(1). 1–38. DOI: http://doi.org/10.15398/jlm.v10i1.274
Prince, Alan & Smolensky, Paul. 2004. Optimality Theory: Constraint interaction in generative grammar. Oxford: Blackwell Publishing. DOI: http://doi.org/10.1002/9780470759400
Rai, Novel Kishore & Bickel, Balthasar & Gaenszle, Martin & Lieven, Elena & Paudyal, Netra P. & Rai, Ichchha Purna & Rai, Manoj & Stoll, Sabine & Yadava, Yogendra P. 2005. Triplication and ideophones in Chintang. In Yadava, Yogendra P. & Bhattarai, Govinda & Lohani, Ram Raj & Prasain, Balaram (eds.), Contemporary issues in nepalese linguistics, 205–209. Kathmandu: Linguistic Society of Nepal.
Rai, Novel Kishore & Winter, Werner. 1997. Triplicated verbal adjuncts in Bantawa. In Tibetoburman languages of the himalayas, 135–155. Canberra: Pacific Linguistics.
Raimy, Eric. 1999. Representing reduplication. Newark, DE: University of Delaware dissertation.
Raimy, Eric. 2000. The phonology and morphology of reduplication. Berlin: Mouton de Gruyter. DOI: http://doi.org/10.1515/9783110825831
Raimy, Eric. 2006. Review of Inkelas & Zoll 2005: Reduplication: Doubling in morphology. Journal of Linguistics 42(2). 478–486. https://www.jstor.org/stable/4177000. DOI: http://doi.org/10.1017/S0022226706284093
Raimy, Eric. 2011. Reduplication. In van Oostendorp, Marc & Ewen, Colin & Hume, Elizabeth & Rice, Keren (eds.), The Blackwell companion to phonology, vol. 4, 2383–2413. Malden, MA: Wiley-Blackwell. DOI: http://doi.org/10.1002/9781444335262
Raimy, Eric & Idsardi, William. 1997. A minimalist approach to reduplication in Optimality Theory. In Kusumoto, Kiyomi (ed.), Proceedings of north east linguistics society (nels) 27, vol. 27. 369–382. University of Massachusetts, Graduate Linguistic Student Association. https://scholarworks.umass.edu/nels/vol27/iss1/27.
Ritchie, Graeme. 1992. Languages generated by two-level morphological rules. Computational Linguistics 18(1). 41–59.
Roark, Brian & Sproat, Richard. 2007. Computational approaches to morphology and syntax. Oxford: Oxford University Press.
Rogers, James & Heinz, Jeffrey & Fero, Margaret & Hurst, Jeremy & Lambert, Dakotah & Wibel, Sean. 2013. Cognitive and sub-regular complexity. In Morrill, Glyn & Nederhof, Mark-Jan (eds.), Formal grammar, vol. 8036 (Lecture Notes in Computer Science). 90–108. Springer. DOI: http://doi.org/10.1007/978-3-642-39998-5_6
Rogers, James & Pullum, Geoffrey. 2011. Aural pattern recognition experiments and the subregular hierarchy. Journal of Logic, Language and Information 20. 329–342. DOI: http://doi.org/10.1007/s10849-011-9140-2
Rose, Sharon. 1997. Multiple correspondence in reduplication. In Proceedings of the twenty-third Annual Meeting of the berkeley linguistics society: General session and parasession on pragmatics and grammatical structure, 315–326. Berkeley: Berkeley Linguistics Society. DOI: http://doi.org/10.3765/bls.v23i1.1278
Rose, Sharon. 2003a. The formation of Ethiopian Semitic internal reduplication. In Shimron, Joseph (ed.), Language processing and acquisition in languages of semitic, rootbased, morphology, vol. 28, 79–97. Amsterdam & Philadelphia: John Benjamins. DOI: http://doi.org/10.1075/lald.28.04ros
Rose, Sharon. 2003b. Triple take: Tigre and the case of internal reduplication. In San diego linguistics papers, vol. 1, 109–128. San Diego: Department of Linguistics, University of California, San Diego. https://escholarship.org/uc/item/2jz957jm.
Rubino, Carl. 2013. Reduplication. Leipzig: Max Planck Institute for Evolutionary Anthropology. http://wals.info/chapter/27.
Saba Kirchner, Jesse. 2010. Minimal reduplication: University of California, Santa Cruz dissertation. DOI: http://doi.org/10.7282/T3VQ31K8
Saba Kirchner, Jesse. 2013. Minimal reduplication and reduplicative exponence. Morphology 23(2). 227–243. DOI: http://doi.org/10.1007/s11525-013-9225-5
Sande, Hannah. 2017. Distributing morphologically conditioned phonology: Three case studies from guébie. Berkeley, CA: University of California, Berkeley dissertation. https://escholarship.org/uc/item/6tn528r6.
Sande, Hannah. 2021. Morpheme-specific phonology in reduplication. In Proceedings of the Annual Meetings on Phonology, vol. 9. DOI: http://doi.org/10.3765/amp.v9i0.4882
Savitch, Walter J. 1982. Abstract machines and grammars. Boston: Little Brown and Company.
Savitch, Walter J. 1989. A formal model for context-free languages augmented with reduplication. Computational Linguistics 15(4). 250–261.
Seki, Hiroyuki & Matsumura, Takashi & Fujii, Mamoru & Kasami, Tadao. 1991. On multiple context-free grammars. Theoretical Computer Science 88(2). 191–229. DOI: http://doi.org/10.1016/0304-3975(91)90374-B
Smith, Ellen. 2016. Papapana re redu reduplicates: Multiple reduplication in an endangered Northwest Solomonic language. Oceanic Linguistics 55(2). 522–560. DOI: http://doi.org/10.1353/ol.2016.0024
Stabler, Edward P. 2004. Varieties of crossing dependencies: structure dependence and mild context sensitivity. Cognitive Science 28(5). 699–720. DOI: http://doi.org/10.1016/j.cogsci.2004.05.002
Steriade, Donca. 1988. Reduplication and syllable transfer in Sanskrit and elsewhere. Phonology 5(1). 73–155. DOI: http://doi.org/10.1017/S0952675700002190
Stonham, John T. 2007. Nuuchahnulth double reduplication and stratal optimality theory. The Canadian Journal of Linguistics/La revue canadienne de linguistique 52(1). 105–130. DOI: http://doi.org/10.1353/cjl.2008.0020
Struijke, Carolina Maria. 2000. Existential faithfulness: Reduplication, feature displacement, and existential faithfulness: University of Maryland, College Park dissertation.
Terfa, Aor. 2020. Reduplications in the Tiv grammar: Classifications and functions. Journal of Linguistics and Foreign Languages 1(2).
Urbanczyk, Suzanne. 1999. Double reduplications in parallel. In Kager, René & van der Hulst, Harry & Zonneveld, Wim (eds.), The prosody-morphology interface, 390–428. Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/CBO9780511627729.012
Urbanczyk, Suzanne. 2001. Patterns of reduplication in Lushootseed. New York: Garland. https://scholarworks.umass.edu/dissertations/AAI9639045.
Urbanczyk, Suzanne. 2007. Reduplication. In de Lacy, Paul (ed.), The cambridge handbook of phonology, 473–493. Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/CBO9780511486371.021
Urbanczyk, Suzanne. 2011. Reduplication. In Aronoff, Mark (ed.), Oxford bibliographies in linguistics. DOI: http://doi.org/10.1093/obo/9780199772810-0036
van Boven, Cindy. 2021. Phonological restrictions on nominal pluralization in sign language of the netherlands: evidence from corpus and elicited data. Folia Linguistica 55(2). 313–359. DOI: http://doi.org/10.1515/flin-2021-2039
Walther, Markus. 2000. Finite-state reduplication in one-level prosodic morphology. In Proceedings of the 1st north american chapter of the Association for Computational Linguistics conference (NAACL 2000). 296–302. Seattle, Washington: Association for Computational Linguistics.
Wang, Yang. 2021a. Recognizing reduplicated forms: Finite-state buffered machines. In Proceedings of the 18th SIGMORPHON Workshop on Computational Research in Phonetics, Phonology, and Morphology, 177–187. Online: Association for Computational Linguistics. DOI: http://doi.org/10.18653/v1/2021.sigmorphon-1.20
Wang, Yang. 2021b. Regular languages extended with reduplication: Formal models, proofs and illustrations. University of California, Los Angeles MA thesis.
Wilbur, Ronnie B. 2005. A reanalysis of reduplication in American Sign Language. In Hurch (2005) 595–623. DOI: http://doi.org/10.1515/9783110911466.595
Wilbur, Ronnie Bring. 1973. The phonology of reduplication. Bloomington, Indiana: University of Indiana dissertation.
Zhang, Jie & Lai, Yuwen. 2007. Two aspects of productivity in Taiwanese double reduplication. Kansas Working Papers in Linguistics 29. 33–47. DOI: http://doi.org/10.17161/KWPL.1808.1786
Zhang, Zheng-sheng. 1987. Reduplication as a type of operation. In 23rd annual regional meeting ofthe chicago linguistics society, 376–388.
Zimmermann, Eva. 2013. Non-concatenative allomorphy is generalized prosodic affixation: The case of Upriver Halkomelem. Lingua 134. 1–26. DOI: http://doi.org/10.1016/j.lingua.2013.06.001
Zimmermann, Eva. 2021. Faded copies: Reduplication as distribution of activity. Glossa: A journal of general linguistics 6(1). DOI: http://doi.org/10.5334/gjgl.1117
Zukoff, Sam. 2017. Indo-European reduplication: Synchrony, diachrony, and theory. Massachusetts Institute of Technology dissertation. https://dspace.mit.edu/handle/1721.1/113772.
Zuraw, Kie. 2002. Aggressive reduplication. Phonology 19(3). 395–439. DOI: http://doi.org/10.1017/S095267570300441X