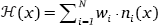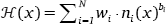1 Introduction
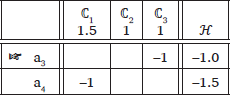
A gang effect has been traditionally defined as a cumulative constraint interaction in which two weaker constraints jointly beat another stronger constraint (Guy 1997; Pater 2009; Albright 2012; Shih 2017). Counter to traditional Optimality Theory (Smolensky & Prince 1993) where constraints are strictly ranked, Harmonic Grammar (Legendre et al. 1990) can capture gang effects without any stipulation, through linear interaction between weighted constraints. Consider the tableaux in (1). In (1)-a and (1)-b, the candidate that violates either ℂ2 or ℂ3 wins since violating ℂ1 is more fatal. In (1)-c, however, the candidate that violates both ℂ2 and ℂ3 loses because the summation of ℂ2 and ℂ3 outweighs ℂ1.
- (1)
- Gang effect
- a.
- w(ℂ1) > w(ℂ2)
- b.
- w(ℂ1) > w(ℂ3)
- c.
- w(ℂ2) + w(ℂ3) > w(ℂ1)
It was reported that the mere addition of constraint weights often cannot capture the cumulative effect correctly because forms with two marked structures occur even less in natural languages than what grammar predicts by multiplying the probabilities of two separate forms with one marked structure each (Albright 2012; Shih 2017; Breiss & Albright 2022). For example, Albright (2012) showed that some combinations of relatively marked structures are strongly underattested in both Lakhota and English. More specifically, singly marked structures are somewhat tolerated in the lexicon but doubly marked structures are not, appearing even more rarely than expected. This super-gang effect calls for an additional penalty for combinations of markedness on top of the sum penalty of dispreferred subparts (Albright 2012). Shih (2017) convincingly showed that super-gang effects can be captured by adding a weighted conjoined constraint in the grammar; the addition of the conjoined constraint significantly improves the grammar’s fit when modeling quantitative natural language patterns. Breiss & Albright (2022), through a series of artificial language experiments, investigated the relationship between the strength of an individual restriction and how it gangs up with other violations. They found that violations are more likely to super-gang up with each other if individual restrictions are weaker, or in other words, have more exceptions. They concluded that a MaxEnt grammar, although best fitting among the contemporary frameworks, can capture these super-gang effects only if very specific weighting conditions are met; the interacting constraints should be both low-weighted.
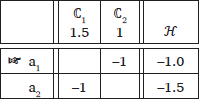
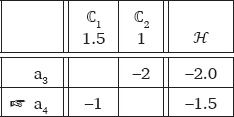
Jäger & Rosenbach (2006) distinguish two types of cumulativity. Ganging-up cumulativity is what most previous works refer to as “gang effects”. As described earlier in (1), it is characterized as a case in which two weaker constraints jointly overcome another stronger constraint. Counting cumulativity refers to cases where multiple violations of a single weaker constraint overpower a single violation of a stronger constraint. In (2)-a, the candidate which violates ℂ1 loses because violating ℂ1 is more severe than violating the weaker constraint ℂ2. However, in (2)-b, the candidate that incurs multiple violations of ℂ2 loses because a single violation of ℂ1 is outweighed by multiple violations of ℂ2.
- (2)
- Counting cumulativity
- a.
- w(ℂ1) > w(ℂ2)
- b.
- w(ℂ2) × 2 > w(ℂ1)
This paper focuses on the super-additive version of this counting cumulativity, which I call super-additive counting cumulativity; multiple violations of a weaker constraint overpower not only a single violation of a stronger constraint, but also go beyond what is predicted by simply multiplying the severity of a single violation of itself. For example, as I will show in §3, an OCP constraint against a pair of laryngeally marked consonants in Korean gangs up in a super-additive manner so that one violation is negligible whereas multiple violations are severe. Throughout the paper, I use the term super-additive cumulativity to refer only to this specific type of gang effect. I report two examples of super-additive counting cumulativity in natural language to show that these effects can be well captured using MaxEnt Harmonic Grammar (Hayes & Wilson 2008) if the penalty is scaled up by the number of violations (n), through a power function (f(n) = nb, where b > 1). I also provide a computational implementation of this framework, called the Power Function MaxEnt Learner, which automatically detects constraints that show super-additive counting cumulativity and learns the appropriate b value.
The remainder of the paper is organized as follows. Through an illustration of a toy example of a super-additive counting cumulativity in §2, I first show that these effects cannot be entirely captured in MaxEnt Harmonic Grammar (Hayes & Wilson 2008). I further show that the super-additivity is better predicted by a MaxEnt grammar provided that a power function is incorporated into the violation assessment method. I also introduce the Power Function MaxEnt Learner, which will be used later in the paper to fit the natural language patterns that show super-additive counting cumulativity. In §3, I investigate a super-additive cumulativity of laryngeally marked consonants in Korean compound tensification, a productive morphophonological process. I analyze the pattern by employing two OCP constraints that are sensitive to the position of a word boundary and to whether the marked structure is derived, and vary in counting cumulativity. In §4, I examine the effects of nasals on blocking Rendaku, a well-known compounding process in Japanese that is similar to Korean compound tensification. Various restrictions in the Rendaku process are attributed to gradient similarity-avoidance effects in Japanese, which are formally analyzed in the paper as a set of OCP constraints on different natural classes and with varying degrees of counting cumulativity. For each example in §3 and §4, I present learning simulations on the quantitative data acquired from a survey and dictionaries to show that the MaxEnt model detects super-additive constraints and learns appropriate parameters to successfully predict the frequency distributions of the data. I summarize the paper in §5.
2 Super-additive counting cumulativity
I start by defining terms that are used in the paper in §2.1. In §2.2, I present a toy dataset with super-additive counting cumulativity and compare three different violation assessment methods to see how each captures the data. I first analyze the toy data with a conventional penalty assessment method where the product of the constraint weight and the number of violations is summed over all the constraints. I show that super-additivity cannot be entirely captured in a conventional MaxEnt Grammar. In §2.3, I take an alternative approach, a constraint family model, and discuss how it fails to capture monotonicity of such patterns wherein more violations incur more severe penalties. In §2.4, I introduce the power function model in which the degree of penalty is scaled up according to the number of violations, through a power function. In §2.5, I introduce a MaxEnt implementation of the power function model, called the Power Function MaxEnt Learner, with a focus on how it differs from the conventional MaxEnt learner. I present two learning simulations to show the capacity of this learner. I first fit a dataset without super-additive counting cumulativity using the Power Function MaxEnt Learner; I show that the learner successfully lets all the b values stay at 1. Subsequently, I fit the super-additive data illustrated in §2.2, showing that the learner is able to detect the super-additive constraint and adjust the parameters accordingly, producing precise frequency matching. I conclude the section by explaining how the property of the power function guarantees a monotonic increase in weights with more violations.
2.1 Terminology
Various terms regarding the topic of constraint interaction have been used in the literature. In this section, I will introduce these terms and determine which of these will be used in the paper.
Ganging and cumulativity have been used interchangeably to refer to an existence of some interaction between multiple violations, either from one constraint or more. As opposed to traditional Optimality Theory (Smolensky & Prince 1993) in which constraints are strictly ranked, Harmonic Grammar (Legendre et al. 1990) and its variations assume that constraints can be ganging or cumulative with each other. I use the terms cumulative and cumulativity in this paper.
Linearity and additivity have both been used in the literature, to refer to types of cumulativity in constraint interaction. According to Breiss & Albright (2022), these terms regard the relationship between the actual probability of doubly-marked structures and the predicted probability of those that is computed by multiplying probabilities of two separate singly-marked structures. They also briefly comment on how linearity is only subtly different from additivity and choose to use the term linearity in keeping with previous literature. Linearity, super-linearity, and sub-linearity refer to cases where the observed probability is equal to, lower than, or higher than the predicted probability, respectively.
As mentioned in §1, this paper focuses on super-additive counting cumulativity, cases where multiple violations of a single constraint overpower a mere multiplication of one violation. As it will be explained in more detail in §2.5, in the conventional MaxEnt grammar, the probability of a certain phonological form x is computed by exponentiating its harmony, the weighted sum of x’s constraint violations (Goldwater et al. 2003; Hayes & Wilson 2008). Because of this exponentiating process, the linear increase in the harmony domain can affect probability in a super-linear manner; nevertheless, simply adding constraint violations is insufficient in some cases, as I will report in the paper. Thus, I use the terminology of additivity in the paper. Specifically, I use the term super-additivity to refer to cases where a monotonic increase in constraint violation cannot fully capture the amount of decrease in the probability domain.
2.2 Conventional MaxEnt Grammar
Tableau (3) illustrates an example that exhibits a super-additive counting cumulativity, motivated by a Korean dataset that will be introduced later in §2. The weights of the constraints and predicted probabilities are computed by the Maxent Grammar Tool (Hayes et al. 2009). Violation of ℂ1 will always be incurred by candidate (ii) and will be constant over the inputs. Violation of ℂ2 will always be incurred by candidate (i), with a monotonic increase. The Korean dataset in §3 will not include inputs like (d) because the majority of Korean native nouns are monosyllabic or disyllabic and therefore not long enough to incur three violations of ℂ2. Even if the word length allows, a co-occurrence of three laryngeally marked consonants is highly disfavored, reported in Park (2020) as phonotactic learning simulation results using the existing Korean native monomorphemic nouns. However, the input (d) is still included for the purpose of demonstration because the expected probability of nonce forms like (3)-d-i is most certainly zero.
- (3)
- Conventional MaxEnt grammar: bad fit
Comparing (3)-a and (3)-b, a single violation of ℂ2 lowers the observed frequency of the winner only marginally and does not reverse the choice of winner. Multiple violations of ℂ2 can reverse the winner, however, as seen in (3)-c and (3)-d. This is a clear case of counting cumulativity, where multiple violations of a weaker constraint ℂ2 overpower a single violation of the more powerful constraint ℂ1. The weighting condition for these two constraints is summarized in (4). The notation w(ℂ) refers to the weight of the constraint ℂ and n refers to the number of violations.
- (4)
- Weighting schema for the counting cumulativity of ℂ2
- w(ℂ2)×n > w(ℂ1) > w(ℂ2), where n ≥ 2
Taking a closer look at the observed probability distributions of (3)-c and (3)-d, the losing candidates with multiple violations of ℂ2 barely occur between the two possible outputs. This shows that ℂ2 is cumulative in a super-additive manner; multiple violations of ℂ2 surpass a mere multiplication of the severity of its single violation.
The weights of the constraints, computed by the Maxent Grammar Tool (Hayes et al. 2009), satisfy the weighting condition given in (4); one violation of ℂ2 (0.6) weighs less than one violation of ℂ1 (0.7), which in turn weighs less than two or three violations of ℂ2 (1.2, 1.8). However, the probabilities of the candidates predicted by the weighted constraints do not successfully match the input distributions. To reproduce the observed pattern of super-additivity, a grammar must satisfy the two following conditions. First, one violation of ℂ2 should weigh low enough to correctly capture the marginal frequency difference between the winners of (3)-a and (3)-b. Second, multiple violations of ℂ2 should weigh high enough to capture the extreme gang-effect in (3)-c and (3)-d. However, this weighted grammar meets neither of these conditions because w(ℂ2) is stuck in the middle; the candidate (3)-b-i was penalized too much for violating ℂ2 once (predicted 52%, while 60% observed) while (3)-c-i was not penalized enough for incurring multiple violations of ℂ2 (38% predicted, while 4% observed).
The simulation illustrates that there is no way for a traditional MaxEnt grammar to satisfy the two conditions: w(ℂ2)×1 being low enough while w(ℂ2)×2 and w(ℂ2)×3 high enough. This is because the disparity between one and multiple violations is wide, but w(ℂ2) is fixed and violations are assessed only linearly. Under this linear strategy, multiple violations are merely doubly or triply penalized, which is not enough to capture the super-additivity.
2.3 Alternative: constraint family
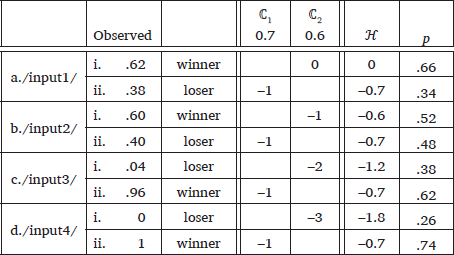
The observed pattern of super-additive counting cumulativity can be captured by a constraint family where a separate self-conjoined constraint is responsible for each number of violations. For the toy data, ℂ2 was replaced by a set of constraints in (5), whose weights were computed using the MaxEnt Grammar Tool (Hayes et al. 2009), as presented in (6).
- (5)
- (ℂ2)1: Penalize exactly one violation of ℂ2.
- (ℂ2)2: Penalize exactly two violations of ℂ2 (=ℂ2&ℂ2).
- (ℂ2)3: Penalize exactly three violations of ℂ2 (=ℂ2&ℂ2&ℂ2).
- (6)
- Constraint family model: good fit
The constraint family provides precise frequency matching, which is expected; there is a separate constraint responsible for every number of violations, and the weight can be adjusted to cater to each input and its candidate distribution.
In this approach, however, constraints that stand for greater numbers of violations are not guaranteed to have higher weight. For example, a constraint family can predict a language in which violating w(ℂ2)3 is less severe than w(ℂ2)1 but more severe than w(ℂ2)2, which is highly unnaturalistic and unattested (e.g., w(ℂ2)1 > w(ℂ2)3 > w(ℂ2)2). A de Lacian approach of stringency hierarchy (de Lacy 2002), where each constraint penalizes n or fewer marked structures, will not have this problem since candidates with one violation will also violate other constraints in the hierarchy such as *TwoOrFewer, *ThreeOrFewer, and so forth. Even this approach, however, only guarantees weak monotonicity; as Jäger & Rosenbach (2006) point out, a stringency hierarchy will predict a language where the probability of the candidates (6)-i is constant at 62% up to 3 violations of ℂ2, decreases to 60% at 4 violations, remains constant until 6 violations and approaches 0% with more. Thus, this line of approaches disregards the nature of super-additive counting cumulativity wherein more violations lead to the strictly lower probability of the offending candidate, as Zymet (2014) notes.
In the same vein, a constraint family also dismisses learners’ abilities to make predictions about larger violations that are not evidenced in the existing lexicon. For example, the Korean native lexicon has very few monomorphemic nouns with two marked consonants, as briefly mentioned in §2.2; however, they know that tensifying a compound formed with these nouns is extremely unlikely.
2.4 Power function
A power function is a function of the form f(a) = ab where the independent variable a is raised to a constant power b. I substitute the number of ℂ2 violations n(ℂ2) with n(ℂ2)b (b > 1) to scale-up the penalty, following Zymet (2014) (scaling of penalty was also used in Coetzee 2009; Pater 2009; Kimper 2011; McPherson & Hayes 2016; Hayes 2017). Here, note that the number of violations is still the same but its contribution to harmony is scaled up. For example, one violation will indicate a severity of 1b while two violations and three violations will indicate 2b and 3b, respectively. Since 1b always equals 1 for any b, application of the power function on the number of violations does not affect the severity of a single violation. If the b value is greater than 1, the penalty is enlarged for multiple violations. Thus, the parameter b is adjusted to serve different degrees of super-additivity; larger b can be used to capture more extreme super-additivity.
With a b value less than 1, the number of violations n is scaled down; nb = 1 when b = 0 and nb < 1 when b is a negative value. In fact, Zymet (2014) exploits a negative power function, in order to capture distance-based decay patterns where the weight of a single constraint is scaled down according to the distance between the interacting segments.
2.5 Power Function MaxEnt Learner
This section outlines the MaxEnt implementation that automatically learns parameters for the power function model introduced in §2.4. In the conventional MaxEnt grammar, harmony of a certain phonological form x is defined as the weighted sum of x’s constraint violations (Goldwater et al. 2003; Hayes & Wilson 2008), shown in (7). Here, N is the number of the constraints, wi is the weight of the ith constraint, ni(x) is the number of times that x violates the ith constraint.
- (7)
The learner of the power function model is crucially different in harmony calculation since the number of violations n(x) is exponentiated by b, as seen in (8). Here, bi is the exponent of the ith constraint. The other components of the learning algorithm remain unchanged from the standard MaxEnt learning algorithm (Hayes & Wilson 2008).
- (8)
The learner’s goal is to find the set of weights that minimizes the negative log likelihood of the training data. Therefore, I formalize learning as minimizing the standard loss function, the sum of the negative log likelihood. For optimization, batch gradient descent is used. The weights for all constraints are initialized at 0 and the b values for constraints are all initialized at 1. From there, each iteration, gradients of the loss function with respect to a given set of weights and b values are determined using the Python library Autograd, which efficiently computes partial derivatives of given functions. Constraint weights as well as the b values are updated based on these gradients, with a learning rate of 0.1 for weights and 0.01 for bs. Notably, with the current set up for bs, in which bs are initialized at 0 and incremented only slowly with a lower learning rate of 0.01, a more conservative assumption about the grammar can be made; that is, every constraint has a linear increase in penalty by default as in regular MaxEnt grammar and only small changes can be made from that initial assumption when the data evidences otherwise (e.g., the existence of super-additivity). If any b values go below 1 after an update, they are automatically reset as 1, because b must be above 1 in order to scale up the number of violation. Similarly, if any weights go below 0 after an update, they are reset as 0. After each update, the loss function is calculated again with the updated parameters. The learner is programmed to terminate whenever the loss function increases rather than decreases.
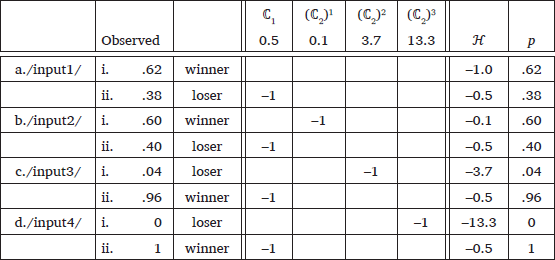
I first fit a dataset without super-additivity in which a linear increase in the number of violations results in a fairly gradual decrease in observed probabilities using the Power Function MaxEnt Learner. In (9), for each input, the observed probability of the candidate (i) gradually decreases with larger violations of ℂ2; the data portrays cases where the counting cumulativity of ℂ2 is no more than additive. The observed probabilities in this tableau are adjusted from (3) for demonstration but this type of gradual decrease/increase in probabilities that arises from violating a scalar constraint is well attested in linguistics (English genitive variation in Jäger & Rosenbach (2006), distance decay in Latin and other languages in Zymet (2014) and Stanton (2016), and Tommo So vowel harmony in McPherson & Hayes (2016)).
- (9)
- Counting cumulativity without super-additivity: good fit
The Power Function MaxEnt Learner converged after 815 iterations and was able to successfully detect that increasing the b for ℂ2 is not necessary; for both constraints, the b values stayed at 1, as shown in (9). Moreover, the learner was able to exactly replicate the weights and the predicted probabilities optimized by the MaxEnt Grammar Tool (Hayes et al. 2009).
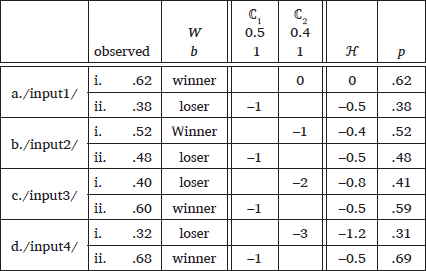
Subsequently, the dataset with super-additivity (3) was fitted using the Power Function MaxEnt Learner. The learner converged after 50,134 iterations. As seen in (10), only the exponent for ℂ2 increased to 4.5 whereas the exponent for ℂ1 stayed at 1, which shows that the learner is able to detect the super-additive constraint given the input data and let b rise only for that constraint. Crucially, it is necessary for the learner to see at least three different levels of scalar violations in the input data in order to determine whether the constraint is super-additive. For example, with (10), the difference between zero and one violation is compared to the difference between one and two violations; since the second step is steeper than the first step in reducing the probability, the learner can confirm that an increased b value of ℂ2 would be beneficial in this case. The parameters in (10) show that the power function approach enables the grammar to reflect the crucial aspects of the super-additive counting cumulativity; a single violation of ℂ2(0.2) is outweighed by a single violation of ℂ1(0.5), which in turn is outweighed by multiple violations of ℂ2(0.2 × 24.5 = 4.5).
- (10)
- Output of the Power Function MaxEnt Learner: good fit
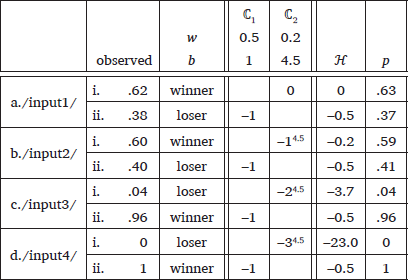
The power function model gives precise frequency matching with an addition of only one parameter on top of a single baseline constraint, which is more parsimonious than a family of constraints in §2.3. Moreover, by relying on the nature of the mathematical concept, the weight is guaranteed to monotonically and strictly increase as the number of violation increases (b > 1).
2.6 Summary
I illustrated a toy example of super-additive counting cumulativity and evaluated three different models: linear assessment, constraint family, and power function. In §2.2, it was shown that the conventional way of assessing violations cannot properly capture super-additivity. In §2.3, a set of self-conjoined constraints provided a good fit to the toy data; but these constraints can be arbitrarily weighted, in which case the observed monotonicity is not guaranteed. In §2.4 and §2.5, a grammar with exponentiated penalties showed a good fit to the toy example. With a slight modification to the traditional MaxEnt model, the Power Function MaxEnt Learner fits the parameters that are necessary for the power function model. More importantly, the mathematical nature of the power function guarantees more violations to be penalized more severely, when the exponent b is larger than 1.
3 Case study 1: laryngeally marked consonants in Korean compound tensification
As the first real-life example that exhibits a super-additive cumulativity, Korean compound tensifcation is investigated in this section. I introduce the phenomenon in §3.1. In §3.2, I analyze the observed pattern using a set of OCP constraints that are sensitive to the position of a word boundary and whether the offending structure is derived or not. The observed super-additivity is attributed to the counting cumulativity of a specific OCP constraint. In §3.3, I report a learning simulation using the Power Function MaxEnt Learner and show that the suggested method correctly captures the observed super-additive pattern.
3.1 Compound tensification and laryngeal OCP
Korean features a distinction between plain consonants (/p/, /t/, /s/, /c/, /k/) and laryngeally marked consonants, which include tense (/p’/, /t’/, /s’/, /c’/, /k’/) and aspirated (/ph/, /th/, /ch/, /kh/), for obstruents. In a compound composed of two nouns, WA and WB, if the initial onset of WB is a plain obstruent, it often undergoes tensification. Tensification is required for some compounds (/san/ ‘mountain’ + /pul/ ‘fire’ [sanp’ul] ‘wild fire’) while not allowed in others (/sil/ ‘thread’ + /panci/ ‘ring’ [silpanci] ‘thread ring’), and there are some compounds that are variably realized as either tensified or non-tensified form (/pul/ ‘fire’ + /kituŋ/ ‘pillar’ [pulkituŋ] ~ [pulk’ituŋ] ‘firestorm’). Zuraw (2010), Ito (2014), and Kim (2017) showed that the tensification probability of a given compound can be predicted by the interaction of various phonological and non-phonological factors, such as frequency, word length, branching structure, and etymology. These authors unanimously reported that tensification is less likely for a compound with a laryngeally marked consonant in it, as in /khoŋ/ ‘bean’ + /ki.rɯm/ ‘oil’ [khoŋ.ki.rɯm], *[khoŋ.k’i.rɯm] ‘soybean oil’ and /tol/ ‘stone’ + /to.k’i/ ‘ax’ [tol.to.k’i], *[tol.t’o.k’i] ‘stone ax’. Considering that the compounding process derives another laryngeally marked consonant in WB, the blocking effect of a laryngeally marked consonant arises from laryngeal co-occurrence restrictions (Ito 2014), or the OCP constraint on the acoustic feature [long VOT] (Gallagher 2011). Please refer to Gallagher (2011) in particular on the grouping of aspirated and tense consonants as a single natural class.
Examining phonological factors that contribute to the likelihood of tensification in Korean compounds, Kim (2017) collected a large-scale pronunciation data by conducting a survey on Seoul Korean speakers. The survey material consists of 304 native noun-noun compounds, whose WB initial onset is a lax obstruent, which are collected from the two data sources: Korean Usage Frequency (Kang & Kim 2009) and the major Korean dictionary (National Institute of Korean Language 1999). In the survey questionnaire, the two components of each compound were given in separate parentheses with the morpheme boundary symbol ‘+’ in between. For each compound, two possible pronunciation forms written in standard Korean orthography, one with and the other without tensification, were given as options. The link for the Google Docs document was sent to 21 participants, who were undergraduate or graduate students of two universities in Seoul (Seoul National University and Yonsei University). They were asked to choose their pronunciations of the word that can be compounded by the two given nouns. The survey generated 6,384 datapoints in total (21 * 304). The overall rate of compound tensification was 57% (3,644/6,384).
Kim (2017) showed that the laryngeal co-occurrence restrictions in compound tensification exhibit different patterns depending on the position (in WA or WB) and the number of laryngeally marked consonants, as summarized in Table 1.
Tensification rate according to the type/number of consonant in WA and WB.
| location | context consonants | tensification | |
| WB | plain/sonorant | .60 | 3,447/5,754 |
| one tense | .31 | 112/357 | |
| one aspirated | .31 | 85/273 | |
| WA | plain/sonorant | .58 | 2,809/4,830 |
| one tense | .62 | 521/840 | |
| one aspirated | .56 | 308/546 | |
| WA | two marked Cs | .04 | 6/168 |
First, the presence of a single laryngeally marked consonant in WB significantly lowers the tensification rate. Unlike the strong effect of a marked consonant in WB, there need to be two marked consonants in WA in order to exhibit sigificant OCP effects; the presence of a single laryngeally marked consonant is not significantly different from the complete absence of any marked consonant on tensification, whereas the presence of two marked consonant in WA lets the tensification rate plunge. If a laryngeally marked consonant is considered a tensification blocker, the effect of two in WA goes beyond doubling the effect of one in WA; two laryngeally marked consonants in WA gang up in a super-additive manner and block tensification.
Analyzing the significance of OCP effects, I constructed a mixed effects logistic regression model using the glmer function from the lme4 package (Bates et al. 2018) in R (Team et al. 2013). The dependent variable was the occurrence of tensification (binary: no tensification (ref), tensification) and the independent variables were the number of marked consonants in WB (backward difference coded: zero, one) and the number of marked consonants in WA (backward difference coded: zero, one, two). The model also included random slopes and random intercepts for participants and compounds. The model is shown in Table 2.
Regression model for the Korean survey results.
| β | SE(β) | z | P | |
| (Intercept) | –3.11 | 0.51 | –6.02 | <0.001 |
| 0 vs. 1 marked consonant in WB | –3.75 | 0.62 | –5.99 | <0.001 |
| 0 vs. 1 marked consonant in WA | 0.00 | 0.39 | 0.00 | 0.99 |
| 1 vs. 2 marked consonants in WA | –5.32 | 1.17 | –4.53 | <0.001 |
In the model reported in Table 2, the coefficients indicate how strongly each factor contributes to decreasing or increasing the likelihood of tensification. The model reflects all the observed OCP effects: (i) a single laryngeally marked consonant in WB significantly reduces the likelihood of tensification, (ii) the presence of one marked consonant in WA has no effect on tensification and is not significantly different from the absence of marked consonant, and (iii) the presence of two marked consonants in WA significantly dampens tensification. Moreover, model comparison using the anova() function revealed that the number of marked consonants in WA makes significant improvements (χ2(2) = 24.3, p < 0.001).
3.2 Analysis: word boundary and counting cumulativity
This section provides a formal analysis of Korean compound tensification. I first introduce constraints that are responsible for the occurrence of tensification. And then, I analyze the OCP pattern observed in §3.1: one laryngeally marked consonant in WB suffices to block tensification while more than one in WA is needed to clearly show the blocking effect. This is attributed to different markedness thresholds in different morphological domains: word and compound.
Traditionally, tensification in Korean compounds has been considered a way of helping a compound be perceived as consisting of two elements (Kim-Renaud 1974; Chung 1980; Ahn 1985). Tensification of the initial segment of WB has been formally described in the literature as an insertion of a stop segment such as /s/ or /t/ at the compound juncture, which would allow an automatic process of post-obstruent tensification, or an insertion of a floating feature that would allow tensification of the following segment, such as [constricted glottis] or [tense]. Among many, following the recent study of Ito (2014), I assume in the paper that a floating [tense] feature is inserted at the compound juncture. Regarding the realization of this [tense] feature, I adopt RealizeMorpheme (Kurisu 2001), which requires that the floating [tense] be realized on some segment. This [tense] feature cannot dock onto the WA final coda, because codas are unreleased and hence cannot be tensified in Korean (Kim-Renaud 1974); the [tense] feature docks onto the WB initial onset segment. While RealizeMorpheme encourages tensification, Id (tense) prevents WB initial onset segments from undergoing tensification, as demonstrated in (11). The weights in the tableau are computed by the MaxEnt Grammar Tool (Hayes et al. 2009).
- (11)
- Compound tensification triggered by RealMorph and blocked by Id (tense)

An offending structure (a co-occurrence of two laryngeally marked consonants) is treated differently depending on whether a word boundary intervenes or not. First, considering that the site of tensification is the initial onset of WB, the reason for the stronger OCP effect in WB is that a co-occurrence of two laryngeally marked consonants is significantly less preferred within a single morpheme. This strong OCP effect in WB can be captured by a trigram that penalizes an offending structure with a preceding word boundary, defined in (12). In the constraint definition, T represents a laryngeally marked consonant and + represents a boundary.
- (12)
- *+TT: Assign a violation mark for every subsequence of a word boundary followed by a laryngeally marked consonant followed by another laryngeally marked consonant.
On the other hand, a laryngeally marked consonant in WA cannot block tensification as strongly because a co-occurrence of two marked consonants is better tolerated in a compound. This can be captured by a similar trigram (13), which penalizes an offending structure with an intervening word boundary.
- (13)
- *T+T: Assign a violation mark for every subsequence of a laryngeally marked consonant followed by a word boundary followed by another laryngeally marked consonant.
The constraint *+TT should be weighted highly enough to capture the clear OCP effect in WB while *T+T should be weighted lowly enough to allow two marked consonants to still co-occur over a word boundary. The OCP pattern of Korean compound tensification corroborates the observation that some phonological restrictions that hold within a morpheme can be loosened or even lifted at morpheme boundaries (Martin 2011; Gallagher et al. 2019).
The tensification-blocking effect of two laryngeally marked consonants in WA is attributed to the counting cumulativity of *T+T violations, as summarized in (14). A single violation of *T+T is outweighed by the tensification-triggering constraint (RealizeMorpheme), which is in turn outweighed by multiple violations of *T+T. Sample tableaux and the weights of the constraints that are computed by the MaxEnt Grammar Tool (Hayes et al. 2009) are shown in (15) and (16). The example in (15), /kochu/ ‘chili’ + /kirɯm/ ‘oil’, represents cases where a marked segment in WA does not block tensification. The example in (16), /k’ochi/ ‘skewer’ + /kui/ ‘roast’, represents cases where two marked consonants in WA block tensification. In these tableaux, the input frequencies are not accurately matched with these weights although they satisfy the weighting condition laid out in (14), because two violations of *T+T are more severe than simply doubling the severity of one violation, indicating that *T+T cumulates in a super-additive manner.1
- (14)
- Counting cumulativity of *T+T
- w(*T+T)×n > w(RealizeMorpheme) > w(*T+T), where n≥2
- (15)
- A single violation of *T+T is weaker than RealizeMorpheme

- (16)
- Two violations of *T+T are stronger than RealizeMorpheme

The constraint *T+T is super-additive only if it is violated by a derived pair of laryngeally marked consonants. Consider tableau (17).
- (17)
- Multiple violations of *T+T not fatal if violated by old pairs

Tableau (17), represented by the example /khoŋ/ ‘bean’ + /kuks’u/ ‘noodle’, illustrates cases where WA and WB both include a laryngeally marked consonant. The candidate with tensification (17)-a still occurs 20% of the time, contrary to (16)-a almost never occurring, although it violates *T+T twice for having two pairs of laryngeally marked consonants over the word boundary: kh+k’ and kh+s’. This is because the underlying T+T subsequence, kh+s’, is tolerated and does not contribute to the super-additivity of *T+T violations. In contrast, the two T+T pairs included in (16)-a, k’+k’ and ch+k’, both contribute to the super-additivity since both include a derived tense consonant k’. Since underlying T+T subsequences behave differently than derived ones, I replace *T+T with *T+TO and *T+TN, as seen in the re-evaluation of the same example from (17), presented in (18). In the tableau, RM represents RealizeMorpheme. Whereas *T+TN is violated by the derived T+T subsequence, *T+TO is violated by the subsequences that are already present in the fully faithful candidate, which are defined as a candidate without violating any faithfulness constraints (Comparative markedness; McCarthy 2003).2 While there is no evidence that *T+TO is super-additive, *T+TN is clearly super-additive.
- (18)
- *T+TN violated by derived subsequences and *T+TO by old subsequences

Making a similar distinction for *+TT is well motivated by the lexical statistics of Korean monomorphemic words. As mentioned earlier, *+TT needs to be weighted highly to capture the significant blocking effect of a marked consonant in WB. However, some combinations of laryngeally marked consonants are actually overrepresented in Korean monomorphemic lexical items. For example, Ito (2014) examined the distribution of consonant types in the onsets of initial and peninitial syllables in Korean simplex nouns. The result showed that the co-occurrence of two tense consonants is overrepresented in the lexicon. Kang & Oh (2016) conducted a similar study with the entire Korean lexicon where the same tendency was found. Underlying TT pairs are either tolerated or even overrepresented tautomorphemically whereas deriving a new tense consonant is avoided in the presence of another marked consonant within a monomorphemic word. This supports a replacement of *+TT with *+TTN and *+TTO, where *+TTN is violated by derived TT pairs and *+TTO is violated by underlying TT pairs that are already present in the fully faithful candidate, which is essentially the input. In the paper, *+TTO is not included in the analysis because the dataset used here has no compound with two underlying marked consonants in WB; *+TTO is vacuously satisfied by all the compounds.
3.3 Learning super-additive counting cumulativity
In this section, I fit the Korean data using the Power Function MaxEnt Learner. I first summarize the necessary constraints. Then, I present the result of the learning simulation on the Korean data. I show that incorporating the power function into violation assessment allows accurate frequency matching of the input data. I also show that the Power Function MaxEnt Learner is able to raise b only for the super-additive constraint and let it remain at 1 for the others.
As mentioned above, I assume that RealizeMorpheme (Kurisu 2001) requires the inserted [tense] feature to be phonologically realized, by the association to the initial onset consonant of WB. In contrast, Ident (tense) requires that the specification for the [tense] feature of the input segments be identical to that of the output segments.
The laryngeal co-occurrence patterns are captured by a set of two OCP constraints, which penalize derived marked pairs with a preceding or intervening word boundary, as defined again in (19) and (20). The counterpart constraints *T+TO and *+TTO are excluded in the analysis as these constraints are not decisive in predicting candidate distributions; *+TTO is never violated in the entire dataset as mentioned above and *T+TO is violated by either all candidates or no candidates for each input.
- (19)
- *+TTN: Assign a violation mark for every subsequence of a word boundary followed by a laryngeally marked consonant followed by another laryngeally marked consononant that is not present in the input.
- (20)
- *T+TN: Assign a violation mark for every subsequence of a laryngeally marked consonant followed by a word boundary followed by another laryngeally marked consonant that is not present in the input.
The Korean data was fitted using the Power Function MaxEnt Learner. The weights of the constraints were all initialized at 0. The update to a constraint’s weight was the negative of the learning rate (0.1) times the gradient that was computed by Autograd each iteration. The b values for each constraint were also all initialized at 1. The update to a constraint’s exponent b was the negative of the learning rate (0.01) times the gradient that was computed by Autograd each iteration. The learner converged after 39,587 iterations. The resulting set of weights and exponents are shown in (21). In the inputs and outputs, T represents a syllable with a laryngeally marked consonant whereas σ represents a syllable without one. The other factors that could potentially be relevant to the likelihood of tensification, such as the word length and the position of laryngeally marked segments, were not significant in the statistical analysis above and were disregarded in this paper. For instance, the input in (21)-d represents words of any length, which is either 3 or 4 syllables long in the data, whose WB underlyingly has a single laryngeally marked segment.
In the tableau, only the exponent for the super-additive constraint *T+TN increased to 4.5 whereas those for all the other constraints stayed at 1, which shows that the learner is able to detect the super-additive constraint given the input data and let b rise only for that constraint. With these weights and powers, the grammar reproduced the observed pattern closely.
- (21)
- Output of the Power Function MaxEnt Learner: good fit
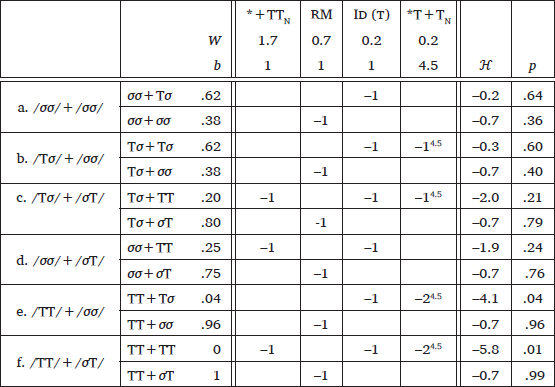
The fact that one violation of *T+TN has no effect of blocking tensification is reflected in the very low weight of *T+TN (w = 0.2). Also, the large disparity between one and two violations of *T+TN is reflected in its exponent 4.5. With these parameters, the weighted grammar correctly captures the super-additive counting cumulativity of *T+TN: one violation of *T+TN (w = 0.2) is outweighed by the tensification triggering constraint (w = 0.7), which in turn is much outweighed by multiple violations of *T+TN (w = 0.2 * 24.5 = 4.5).
3.4 Summary
In this section, I investigated super-additivity of laryngeally marked consonants in Korean compound tensification, a process whereby the initial onset of WB can be tensified when compounded. The tensification likelihood of a given compound can be partially predicted a number of phonological factors, one of which is the presence of another marked consonant, motivated by laryngeal co-occurrence restrictions. Co-occurrences of marked consonants are tolerated differently in different morphological domains (word and compound); whereas a single laryngeally marked consonant in WB blocks tensification, there must be two marked consonants in WA to block the process. The observed OCP patterns were captured by multiple OCP constraints that are sensitive to the position of the word boundary and the input-output mappings, one of which (*T+TN) was super-additive and therefore responsible for the super-additive cumulativity of a marked consonant in WA. The Power Function MaxEnt Learner was able to detect this constraint as super-additive and adjusted the parameters, successfully matching the frequencies of the input data.
4 Case study 2: nasals in Japanese Rendaku
As another case of super-additive counting cumulativity, nasals in Japanese Rendaku are investigated in this section. I provide a brief introduction of the process in §4.1. I describe the compound databases that I use and report some tendencies found in the data in §4.2. In §4.3, I give a phonological analysis of the observed pattern using OCP constraints that operate on different natural classes, one of which cumulates super-additively. In §4.4, I use the Power Function MaxEnt Learner to fit the Japanese data. I summarize the section in §4.5.
4.1 Background: Rendaku and Lyman’s Law
In a compound composed of two elements (WA and WB) in Japanese, if the second element begins with a voiceless obstruent (/t/, /s/, /k/, /h/), it often voices (/jama/ ‘mountain’ + /kata/ ‘area’ → [jamaɡata] ‘mountain area’). It is a tendency that can be predicted by various phonological and non-phonological factors, extensively studied in previous literature (Itô & Mester 1986; Kawahara & Sano 2014b, and many others).
One of the best known factors is the presence of a voiced obstruent in WB; if WB already contains a voiced obstruent (/b/, /d/, /z/, /ɡ/), Rendaku is almost always blocked (/jama/ ‘mountain’ + /kazi/ ‘fire’ → [jamakazi] *[jamaɡazi] ‘mountain fire’). This is related to Lyman’s Law (Lyman 1894), which states that a stem must not contain more than one voiced obstruent. This pattern has been formally accounted for through the OCP effect or co-occurrence restrictions on the voice feature (Itô & Mester 1986).
4.2 Corpus study
I employ two complementary compound databases for investigating various phonological restrictions of Rendaku in this paper. The main database that I use, Irwin et al. (2020), is a collection of all 35,328 Rendaku candidate compounds that are found in two major dictionaries, Kenkyūsha (Watanabe et al. 2008) and Kōjien (Shinmura 2008). Here, Rendaku candidate compounds refer to the compounds whose WB begins with a voiceless obstruent and does not include a voiced obstruent. The database provides the compounds’ pronunciations that can be retrieved from either or both of those two dictionaries and I work with the pronunciation data sourced from the Kenkyūsha dictionary in this paper. I included compounds whose pronunciations in Kenkyūsha are either specified as “+”, meaning Rendaku is exhibited, or “–”, meaning Rendaku is not exhibited. I excluded compounds whose pronunciations are not available in Kenkyūsha or annotated as “+–”, meaning that both Rendaku and non-Rendaku pronunciations are possible, in order to treat Rendaku application as a binary variable.
As I am investigating phonological restrictions of Rendaku, I excluded items that could potentially be affected by other factors that have been reported to dampen Rendaku. Irwin et al. (2020) not only includes noun-noun compounds but also those that are comprised of verbs or adjectives; I excluded compounds that are only comprised of verbs as these rarely undergo Rendaku (Okumura 1955; Vance 2008; Irwin 2012). Irwin et al. (2020) includes compounds with elements from any of the Japanese lexical strata: Yamato (native), Sino-Japanese, or foreign. I only included compounds whose WB is from the native stratum, as it has been reported that WB from either the Sino-Japanese or the foreign stratum can resist Rendaku (Vance 2007; Irwin 2005; 2011). It has been noted in the literature that Rendaku is only applicable to elements on the rightmost branch of the morphological tree (Right Branching Condition; Itô & Mester 1986; Otsu 1980). I included compounds where WB is written with exactly one Kanji character in order to eliminate the effect of the Right Branching Condition. For example, compounds with /kanamono/ (金物) ‘hardware’ or /tatemono/ (建物) ‘building’ as the second noun were excluded. It is not the perfect metric for determining the monomorphemicity of a word because there are simplex words that can be written with two Kanji characters, as Tanaka (2017) points out, but it definitely guarantees that WB is monomorphemic and the initial segment of WB belongs to the right branch of the compound.
I also excluded coordinate compounds, as they are known to systematically avoid Rendaku application (Okumura 1955). Lastly, I only include compounds whose WB is three moras or longer. The process above resulted in an ideal dataset for investigating phonological restrictions on Rendaku. The data includes 2,130 items, of which 1,772 underwent Rendaku (83%).
Since compounds with a voiced obstruent in WB are already excised from the main database Irwin et al. (2020), I obtained another database: Rosen (2018). This database consists of 645 Yamato compounds with an initial voiceless obstruent in WB, whose total moraic count does not exceed four. Rosen (2018) and the equivalent subset of Irwin et al. (2020), which is restricted to 4,519 Yamato noun-noun compounds that fall within the same length limit (<5μ), are highly comparable in terms of the Rendaku probabilities under different phonological conditions; (i) no voiced obstruent in WB: 78% vs. 75%, (ii) no nasal in WB: 75% vs. 72%, (iii) one nasal in WB: 85% and 87%, and Rosen (2018) include no compounds with two nasals in WB. Therefore, I use the counts and Rendaku probability obtained from Rosen (2018) for the category of compounds with one voiced obstruent in WB. With these items included in the extracted Irwin et al. (2020) dataset, the overall Rendaku probability shows a slight decrease (79%; 1,772 out of 2,246), as none of these 116 added items undergo Rendaku.
The Rendaku probability depends on the type and number of context consonants, as summarized in Table 3. First, the most influential factor in Rendaku, the effect of Lyman’s Law, was confirmed in the corpus data; the presence of one voiced obstruent in WB can categorically block Rendaku. Unlike the strong effect of voiced obstruents, it has been described in the literature that the presence of a nasal in WB does not block Rendaku (Rice 2005), as in /kaza/ ‘wind’ + /kuruma/ ‘car’ → [kazaguruma] ‘windmill’. This traditional observation was confirmed in the corpus data; for the 2,129 compounds that do not contain any voiced obstruents, the presence of a single nasal is different from the absence of nasals in Rendaku by only 4.4%. However, two or three nasals in WB can heavily dampen Rendaku, as in /touzoku/ ‘thief’ + /kamome/ ‘seagull’ → [touzokukamome] ‘pomarine jaeger (a type of seabird)’ and /hito/ ‘one’ + /tsumami/ ‘knob’ → [hitotsumami] ‘easy victory’. If we regard a nasal consonant as a Rendaku blocker, the effect of two blockers goes beyond merely doubling the effect of one; two nasals in WB cumulate in a super-additive manner and block the application of Rendaku.3
Analyzing the significance of the observed nasal effects, I constructed a logistic regression model using the glm function from the lme4 package (Bates et al. 2018) in R (Team et al. 2013). The occurrence of Rendaku was the dependent variable (binary: no Rendaku (ref), Rendaku) and the number of nasals in WB (backward difference coded: zero, one, two or more) was the independent variable. The result is shown in Table 4.
Regression model for the Rendaku database.
| β | SE(β) | z | p | |
| Intercept | 1.06 | 0.13 | 8.10 | <0.001 |
| 0 nasal vs. 1 nasal | –0.30 | 0.13 | –2.32 | <0.05 |
| 1 nasal vs. 2 nasals | –1.34 | 0.38 | –3.46 | <0.001 |
In the model, a negative coefficient means that the factor contributes to dampening Rendaku and the larger absolute value means that the effect is stronger. As can be seen in Table 4, the presence of a single nasal significantly reduces the likelihood of Rendaku application but the presence of two nasals exerts an even bigger effect in reducing Rendaku probability. Note that the regression model here is based on the extracted database (2,130 items), in which potential effects of the known confounding factors, such as Right Branching Condition, are removed. I ran another regression model with a larger database, which includes all the 2,130 compounds used in the model 4 as well as 312 compounds that had to be excluded due to their polymorphemic WB (= 2,442 items in total). The model is reported in Table 5.
Regression model with Right Branching Condition as an extra predictor.
| β | SE(β) | z | p | |
| Intercept | 0.26 | 0.15 | 1.69 | <0.1 |
| 0 nasal vs. 1 nasal | –0.32 | 0.11 | –2.79 | <0.01 |
| 1 nasal vs. 2 nasals | –1.23 | 0.33 | –3.75 | <0.001 |
| Right Branching Condition | 0.82 | 0.13 | 6.07 | <0.001 |
As can be seen, the effect of Right Branching Condition is clearly present, which is compatible with the traditional description on Rendaku: Rendaku is more likely with a monomorphemic WB. However, this model also reveals that the nasal effects are still significant even if the Right Branching Condition is included in the model. Moreover, model comparison using the anova() function also showed that the addition of the number of nasals in WA makes significant improvements to the fit to the data (χ2(2) = 27.86, p < 0.001). This confirms that the Rendaku-dampening effect of two nasals in WB is robust in the lexicon of Japanese.
Kumagai (2017a) is the first study that reports the significant Rendaku-blocking effect of a sequence of nasals, discovered through a nonce word experiment. A larger nonce word experiment was recently carried out by Kawahara & Kugamai (2021), re-examining the Rendaku-blocking effect of two nasals. The general trend in their result is compatible with the nonceword study of Kumagai (2017a) and my corpus data; Rendaku probability was indeed lowered by two nasals but not by one. However, the effect of two nasals was not statistically significant in their experiment. Hopefully future research will explain why the nasal effect was not significant in the experiments of Kawahara and Kugamai.
4.3 Analysis: similarity avoidance and counting cumulativity
In this section, I first introduce constraints that are responsible for the occurrence of Rendaku. Then, I give a formal analysis of the patterns described in §4.2. I explain why a single nasal would still tolerate the application of Rendaku whereas a single voiced obstruent and multiple nasals would significantly lower the Rendaku probability in WB, by making a connection to previously established similarity avoidance effects in Japanese; higher similarity between surface segments is more strongly avoided. I define OCP constraints that operate on different natural classes, one of which is responsible for the super-additive cumulativity of nasals.
Similar to the Korean compound tensification case, it is assumed that the compound juncture marker [+voice] is inserted between two nouns when they form a compound. The constraint RealizeMorpheme is responsible for the [+voice] feature to be realized (Kurisu 2001), by the association to the initial onset consonant of WB, whereas Ident (voice) blocks voicing.
The resistance to Rendaku increases if the Rendaku process results in a co-occurrence of more similar segments. Table 6 illustrates how the presence of a single nasal, two nasals, and a voiced obstruent in WB differently contribute to the overall similarity between consonants with the application of Rendaku. If /tene/ undergoes Rendaku, it results in a co-occurrence of consonants that agree in one feature out of two. This degree of similarity (50%) is presumably tolerable since Rendaku still applies in this case. However, if /teɡe/ underwent Rendaku, it would generate two overlapping feature pairs, which is a total identity in this case (100%). Likewise, the application of Rendaku on /teneme/ would result in 4 overlapping feature pairs out of 6 possible pairs (67%; [+voice]×3, [+sonorant]×1). In the last two cases, the degree of similarity would be intolerably high if Rendaku applied and therefore Rendaku does not take place. The number of overlapping features is not a perfect way of measuring similarity since some features are more perceptually salient than others (Kawahara 2007) but I use this metric for the simplicity of analysis since more overlapping features definitely guarantee a higher similarity.
Feature specification of hypothetical Rendaku-applied WB forms.
| UR Rendaku | /tene/ [dene] | /teɡe/ *[deɡe] | /teneme/*[deneme] | ||||
| consonant tier | d | n | d | ɡ | d | n | m |
| voice | + | + | + | + | + | + | + |
| sonorant | – | + | – | – | – | + | + |
The effect of similarity avoidance on Rendaku applicability has been frequently brought up in the literature. Kawahara & Sano (2014b) showed through a nonce word experiment that Rendaku is both blocked and triggered by an output constraint that bans a co-occurrence of two identical CV morae; Rendaku is less likely if it creates a total identity of two consecutive morae over the boundary (/iɡa/+/kaniro/ → [iɡakaniro], *[iɡaɡaniro]) and more likely if it underlyingly contains two identical CV morae (/ika/+/kaniro/ → [ikaɡaniro], *[ikakaniro]). By the same token, Kawahara & Sano (2014a) showed that Rendaku is more likely to be blocked if it results in two consecutive identical CV morae in WB (WA+/tadanu/ → [WAtadanu], *[WAdadanu]). Thus, the application of Rendaku is a way of either resolving or preventing identity at the moraic level. Moreover, there is a growing body of experimental studies proving that the similarity avoidance effect is gradient and that higher similarity tends to be more strongly avoided. Sano (2013) showed that identity at the segmental level (e.g. CiVz.CjVz) is avoided but total identity (CiVz.CiVz) is even more strongly avoided in Japanese verbal inflection. Kumagai (2017b) chose subsidiary features for a similarity measure and argued that the Rendaku-blocking effect strengthens when more features overlap. For example, a nonce compound /nise/ + /haϕɯra/ ([nisebaϕɯra]) has a higher chance of Rendaku application, compared to /nise/ + /hamara/ ([nisebamara]), because [b… ϕ] shares [+lab] whereas [b…m] also shares [–continuant] on top of [+lab].
In order to capture the different Rendaku-blocking effects of nasals and voiced obstruents, I employ OCP constraints that are defined over two sets of segments: voiced consonant and voiced obstruent. As stated by the gradient similarity-avoidance effects, the strength of these constraints depends on the homogeneity of the natural class the constraint is defined over; voiced obstruents ([bdzɡ]) are more homogenous than voiced consonants ([bdɡzmnjwr]), and the OCP constraint on voiced obstruents is stronger.
First, the OCP constraint that bans a co-occurrence of two voiced consonants is defined in (22). In the constraint definition, C̬ is used to represent any consonant that is voiced ([+voice, +consonantal]). This constraint is responsible for blocking Rendaku application with a nasal in WB. The weights computed by the MaxEnt Grammar Tool (Hayes et al. 2009) are shown in sample tableaux (23)–(24). Throughout the section, tableaux with abstract inputs will be presented in order to show the overall trend in the lexicon instead of the behavior of individual items. Since this paper only focuses on the effects of WB consonants on Rendaku, the first element of the compound is represented as an abstract form WA. The second element is represented by three consecutive CV moraic units, or light syllables (e.g., CVCVCV). For the simplicity, syllables with a voiced obstruent will be represented by D, syllables with a nasal will be represented by N, syllables with neither will be represented by σ.
- (22)
- *+C̬C̬: Assign a violation mark for every subsequence of a word boundary followed by a voiced consonant followed by another voiced consonant.
- (23)
- One violation of *+C̬C̬ allows Rendaku application most of the time

- (24)
- Multiple violations of *+C̬C̬ dampen Rendaku application

The Rendaku-applied candidate (23)-a violates *+C̬C̬ once for containing a subsequence of voiced consonants, such as [d…n], and occurs 80% of the time. Considering that the compounds with no nasal in the corpus data underwent Rendaku 85% of the time as reported in Table 3, *+C̬C̬ must be low-weighted enough to allow the candidate (23)-a to occur as almost frequently as candidates with no violation of *+C̬C̬. Multiple violations of *+C̬C̬, however, can be more fatal, as shown in (24). Candidate (24)-a violates *+C̬C̬ three times for having three distinctive pairs of segments that are [+voice, +consonantal]: such as [d…n1], [d…n2], and [n1…n2]. Compared to candidate (23)-a occurring 80% of the time, candidate (24)-a occurs only 52% of the time because three violations of *+C̬C̬ is more severe than simply tripling the severity of one violation, indicating that *+C̬C̬ is cumulative in a super-additive way.
The weighting condition between *C̬C̬ and RealizeMorpheme to capture the observed counting cumulativity is summarized in (25). The weights in the tableaux, computed by the MaxEnt Grammar Tool (Hayes et al. 2009), do not satisfy this weighting condition; the current weighted grammar inaccurately predicts that the Rendaku-applied candidate (24)-a occurs 70% of the time.
- (25)
- Counting cumulativity of *+C̬C̬
- w(*+C̬C̬)×n > w(RealizeMorpheme) > w(*+C̬C̬), (n ≥ 3)
The categorical Rendaku-blocking effect of a voiced obstruent is captured by the constraint defined in (26). In the definition, D is used to represent any segment that is [+voice, –sonorant]. Thus, this constraint will penalize co-occurrences of [bdzɡ]…[bdzɡ] in WB. A sample evaluation is provided in (27).
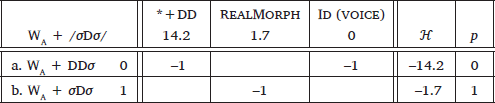
- (26)
- *+DD: Assign a violation mark to every subsequence of a word boundary followed by a voiced obstruent followed by another voiced obstruent.
- (27)
- No Rendaku applied when WB has one voiced obstruent
Unlike the Korean case where the OCP constraint needed to be sensitive to whether the offending structure is derived, Japanese does not require *+C̬C̬ to be separated into *+C̬C̬N and *+C̬C̬O because the constraint *+C̬C̬ is consistently inert in both dynamic alternations and static phonotactic restrictions of Japanese; as we just observed, a single nasal in WB does not inhibit Rendaku, which implies that *+C̬C̬ is not powerful enough to work against the morphophonological alternation. Moreover, it is violated fairly frequently in existing words, as there are stems where two nasals freely co-occur (/mono/ ‘object’).
4.4 Learning super-additive counting cumulativity
In this section, I present the result of a learning simulation on the Japanese data to show that incorporating the power function into violation assessment enables the grammar to accurately match the frequencies of the data with super-additive counting cumulativity. I also show that the Power Function MaxEnt Learner is able to detect the super-additive constraint and raise the b value only for that constraint, while letting b remain as 1 for the others.
As mentioned above, I adopt RealizeMorpheme (Kurisu 2001) and Ident (voice) as the constraints that are responsible for the application of Rendaku. Different Rendaku-blocking effects of nasals and voiced obstruents in WB are captured by a set of OCP constraints: *C̬C̬ and *DD.
The Japanese database was fitted using the Power Function MaxEnt Learner. Weights and exponents of the constraints were initialized and updated the same way as in the Korean simulation. The learner converged after 13,280 iterations. The resulting set of weights and exponents, as well as the fit of the grammar to the data are reported in (28). As mentioned above, tableau (28) is only showing the phonological contexts of WB. To reiterate, D represents a light syllable with a voiced obstruent, N represents a light syllable with a nasal consonant, and σ represents a light syllable with neither in the input and output forms. Similarly to the Korean case study, other phonological factors, such as the position of Rendaku blocking segments, were disregarded here. Thus, for example, input (28)-b represents the cases where a trimoraic/trisyllabic WB underlyingly has a single nasal consonant.
- (28)
- Output of the Power Function MaxEnt Learner: good fit
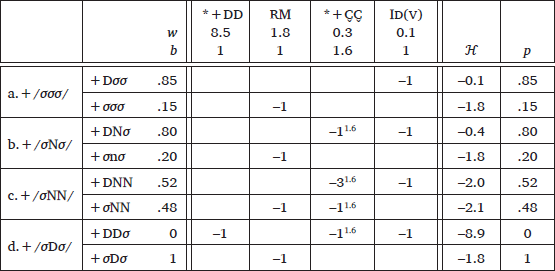
The Power Function MaxEnt Learner successfully detected the super-additive constraint, *+C̬C̬, and raised the exponent for that constraint only. The adjusted exponents and the weighted constraints correctly capture the crucial aspects of the observed Rendaku patterns. First, the nearly inviolable restriction of Lyman’s Law is reflected by the high weight of *+DD. Second, RealizeMorpheme (w = 1.8) outweighs a single violation of *+C̬C̬ (w = 0.3), which reflects the observation that a single nasal does not severely reduce Rendaku application. In turn, three violations of *+C̬C̬ (w = 0.3*31.6 ≈ 2), which are incurred by a WB with two nasals undergoing Rendaku, outweigh RealizeMorpheme, correctly capturing the stronger Rendaku-dampening effects of multiple nasals. With these parameters, the grammar successfully reproduced the observed frequency distributions.
4.5 Summary
In this section, the effects of nasals on blocking Rendaku were examined. The presence of one voiced obstruent in the second element significantly blocks voicing due to Lyman’s Law (Lyman 1894), which states that stems must not contain more than one voiced obstruent. Nasals show a super-additive counting cumulativity in blocking the voicing process; whereas one nasal in the second noun only slightly lowers the likelihood of Rendaku, two nasals cumulate in a super-additive manner and significantly dampen Rendaku application. The observed patterns were attributed to a gradient similarity-avoidance effect in Japanese, which is formally analyzed by a set of OCP constraints that operate on different natural classes with varying degrees of counting cumulativity. I presented a learning simulation on the quantitative data and showed that the Power Function MaxEnt Learner successfully detected the super-additive constraint and matched the input distributions.
5 Conclusions
This paper investigated a type of cumulativity observable in natural languages, called super-additive counting cumulativity, where multiple violations of a weaker constraint go beyond a mere multiplication of its own severity. I demonstrated through a toy example that the super-additivity in counting cumulativity cannot be entirely captured by the traditional MaxEnt grammar where violations are assessed linearly. Instead, a slight modification was made to the conventional violation assessment method to accommodate this specific case; a power function f(a) = ab was applied to the number of violations in order to scale up the penalty (b > 1). The advantage of the power function model is best recognized when compared to the alternative, a constraint family model; whereas a constraint family employs a set of self-conjoined constraints that can be all independently and arbitrarily weighted, the power function model internalizes counting cumulativity by relying on the nature of the mathematical concept, in which the weights are guaranteed to increase strictly and monotonically with a larger number of violations.
I reported two natural language examples that show super-additive counting cumulativity. In a compounding process of Korean and Japanese, the initial onset of the second element undergoes an alternation. The presence of marked consonants inhibits the likelihood of this alternation, motivated by OCP constraints, in a super-additive manner; the presence of one only has negligible effects whereas the presence of two significantly dampens the alternation process. The negligible effect of one violation was analyzed in Korean as the morpheme-internal restriction being weakened over a morpheme boundary (e.g., w (*+TT) > w (*T+T)), and in Japanese as a weaker co-occurrence restriction on a natural class that is less homogeneous (e.g., w (*+DD) > w (*+C̬C̬)). In the analysis, I associated these weaker constraints with super-additivity, which is why multiple violations of these can block the process.
This paper also has provided an implementation of the modified MaxEnt model which learns exponents and weights of the constraints. Learning simulations on the quantitative data obtained from a survey and a corpus show that the implemented MaxEnt learner successfully detected super-additive constraints and raised the exponents only for those constraints. With the adjusted parameters, the MaxEnt model was able to reproduce the probabilistic candidate distributions.
Notes
- One of the reviewers asked if the common alternative, tier-based local constraints, as opposed to constraints against offending subsequences, could be an option here. The observed pattern can certainly be reproduced by an alternative approach. For example, I can suppose a tier on which only the actively interacting segments, laryngeally marked consonants and the morpheme boundary, are visible. If I attend to substrings on this tier, the difference between the candidate (15)-a and the candidate (16)-a will have to be made by introducing another constraint *TT+T, which penalizes (16)-a and not (15)-a. The candidate (16)-a would then incur one violation of *TT+T on top of one violation of *T+T, rather than incurring two violations of *T+T. While the weight of *T+T would capture the small OCP effect and the weight of *TT+T would capture the maximized OCP effect, successfully reproducing the observed input distributions, grammars with these constraints are not guaranteed to give *TT+T greater weight than *T+T, which can lead to typological pathologies like the one described in §2.3. By contrast, if I attend to subsequences and assign multiple violation of one constraint for the candidate (16)-a, the weights are guaranteed to monotonically increase with more violations, under my proposed power function approach. [^]
- Among other frameworks that deal with derived environments, I use this specific approach of Comparative Markedness for the simplicity and the ease of presentation. [^]
- One of the reviewers asked if two liquids and two approximants also can contribute to blocking Rendaku. The current dataset does not allow a clear investigation of these effects due to the lack of relevant data but it is likely that those effects exist. First, of 51 compounds with two /r/s in WB, only 7 (14%) undergo voicing; but all of these examples can be explained away by either having a verb as WB or having a tautomorphemic WB, violating the Right Branching Condition. Second, while there were no compounds with two approximants in WB in the current database, the recent nonceword study by Kawahara & Kugamai (2021) found a significant super-additive cumulativity of two approximants in blocking Rendaku. Moving forward, I focus on the nasals in the paper because of the insufficient data and leave investigating the effects of other sonorants to future study. [^]
Acknowledgements
My special thanks go to Michael Becker for his wonderful advising. I also thank Gaja Jarosz and Max Nelson for their help with the development of my MaxEnt learner. I appreciate the associate editor as well as three anonymous reviewers for insightful comments and helpful feedback. The Japanese portion of this project would have been impossible on my own. Specifically, I deeply thank Mark Irwin and Eric Rosen for kindly letting me use their databases. I also received tremendous help from my Japanese colleagues in linguistics: Chikako Takahashi, Hironori Katsuda, Mari Kugemoto, and Yosho Miyata. Remaining errors are all my own.
Competing interests
The author has no competing interests to declare.
References
Ahn, Sang-Cheol. 1985. The interplay of phonology and morphology in Korean: University of Illinois at Urbana-Champaign dissertation.
Albright, Adam. 2012. Additive markedness interactions in phonology. A handout presented at UCLA linguistics colloquium.
Bates, Douglas & Maechler, Martin & Bolker, Ben & Walker, Steven & Christensen, Rune Haubo Bojesen & Singmann, Henrik & Dai, Bin & Scheipl, Fabian & Grothendieck, Gabor & Green, Peter. 2018. Package ‘lme4’. Version 1(17). 437.
Breiss, Canaan & Albright, Adam. 2022. Cumulative markedness effects and (non-)linearity in phonotactics. Glossa: a journal of general linguistics 7(1). DOI: http://doi.org/10.16995/glossa.5713
Chung, Kook. 1980. Neutralization in Korean: A functional view: The University of Texas at Austin dissertation.
Coetzee, Andries W. 2009. An integrated grammatical/non-grammatical model of phonological variation. Current issues in linguistic interfaces 2. 267–294.
de Lacy, Paul Valiant. 2002. The formal expression of markedness: dissertation.
Gallagher, Gillian. 2011. Acoustic and articulatory features in phonology–the case for [long VOT]. DOI: http://doi.org/10.1515/tlir.2011.008
Gallagher, Gillian & Gouskova, Maria & Camacho Rios, Gladys. 2019. Phonotactic restrictions and morphology in Aymara. Glossa. DOI: http://doi.org/10.5334/gjgl.826
Goldwater, Sharon & Johnson, Mark & Spenader, Jennifer & Eriksson, Anders & Dahl, Östen. 2003. Learning OT constraint rankings using a maximum entropy model. In Proceedings of the stockholm workshop on variation within optimality theory, vol. 111. 120.
Guy, Gregory R. 1997. Violable is variable: Optimality theory and linguistic variation. Language Variation and Change 9(3). 333–347. DOI: http://doi.org/10.1017/S0954394500001952
Hayes, Bruce. 2017. Varieties of noisy harmonic grammar. In Proceedings of the annual meetings on phonology, vol. 4. DOI: http://doi.org/10.3765/amp.v4i0.3997
Hayes, Bruce & Wilson, Colin. 2008. A maximum entropy model of phonotactics and phonotactic learning. Linguistic inquiry 39(3). 379–440. DOI: http://doi.org/10.1162/ling.2008.39.3.379
Hayes, Bruce & Wilson, Colin & George, Ben. 2009. Maxent grammar tool. Java program downloaded from http://www.linguistics.ucla.edu/people/hayes/Maxent-GrammarTool.
Irwin, Mark. 2005. Rendaku-based lexical hierarchies in Japanese: The behaviour of Sino-Japanese mononoms in hybrid noun compounds. Journal of East Asian Linguistics 14(2). 121–153. DOI: http://doi.org/10.1007/s10831-004-6306-9
Irwin, Mark. 2011. Loanwords in japanese, vol. 125. John Benjamins Publishing. DOI: http://doi.org/10.1075/slcs.125
Irwin, Mark. 2012. Rendaku dampening and prefixes. NINJAL Research Papers 4. 27–36.
Irwin, Mark & Miyashita, Mizuki & Russell, Kerri & Tanaka, Yu. 2020. The Rendaku Database v4.0.
Ito, Chiyuki. 2014. Compound tensification and laryngeal co-occurrence restrictions in Yanbian Korean. Phonology 31(3). 349–398. DOI: http://doi.org/10.1017/S0952675714000190
Itô, Junko & Mester, Ralf-Armin. 1986. The phonology of voicing in Japanese: Theoretical consequences for morphological accessibility. Linguistic inquiry 49–73.
Jäger, Gerhard & Rosenbach, Anette. 2006. The winner takes it all – almost: Cumulativity in grammatical variation. Linguistics 44(5). 937–971. DOI: http://doi.org/10.1515/LING.2006.031
Kang, Beom-mo & Kim, Heunggyu. 2009. Korean usage frequency. Seoul: Hankookmunhwasa.
Kang, Hijo & Oh, Mira. 2016. Dynamic and static aspects of laryngeal co-occurrence restrictions in Korean. Studies in Phonetics, Phonology, and Morphology 22(1). 3–34. DOI: http://doi.org/10.17959/sppm.2016.22.1.3
Kawahara, Shigeto. 2007. Half rhymes in Japanese rap lyrics and knowledge of similarity. Journal of East Asian Linguistics 16(2). 113–144. DOI: http://doi.org/10.1007/s10831-007-9009-1
Kawahara, Shigeto & Kugamai, Gakuji. 2021. Does Lyman’s Law count? Poster presented at Annual Meetings on Phonology.
Kawahara, Shigeto & Sano, Shin-ichiro. 2014a. Identity avoidance and Lyman’s Law. Lingua 150. 71–77. DOI: http://doi.org/10.1016/j.lingua.2014.07.007
Kawahara, Shigeto & Sano, Shin-ichiro. 2014b. Identity avoidance and Rendaku. In Proceedings of the annual meetings on phonology. DOI: http://doi.org/10.3765/amp.v1i1.23
Kim-Renaud, Young-Key. 1974. Korean consonantal phonology: University of Hawai’i at Manoa dissertation.
Kim, Seoyoung. 2017. Phonological trends in Seoul Korean compound tensification. In Proceedings of the annual meetings on phonology, vol. 4. DOI: http://doi.org/10.3765/amp.v4i0.3994
Kimper, Wendell A. 2011. Competing triggers: Transparency and opacity in vowel harmony: University of Massachusetts Amherst dissertation.
Kumagai, Gakuji. 2017a. Super-additivity of OCP-nasal effect on the applicability of Rendaku. In Glow in asia xi.
Kumagai, Gakuji. 2017b. Testing OCP-labial effect on Japanese Rendaku. Ms. NINJAL.
Kurisu, Kazutaka. 2001. The phonology of morpheme realization: University of California, Santa Cruz dissertation.
Legendre, Géraldine & Miyata, Yoshiro & Smolensky, Paul. 1990. Harmonic grammar-a formal multi-level connectionist theory of linguistic well-formedness: Theoretical foundations. In Proceedings of the twelfth annual conference of the cognitive science society, 884–891. Citeseer.
Lyman, Benjamin Smith. 1894. The change from surd to sonant in Japanese compounds. Oriental Club of Philadelphia.
Martin, Andrew. 2011. Grammars leak: Modeling how phonotactic generalizations interact within the grammar. Language 87(4). 751–770. DOI: http://doi.org/10.1353/lan.2011.0096
McCarthy, John J. 2003. Comparative markedness. Theoretical linguistics 29(1–2). 1–51. DOI: http://doi.org/10.1515/thli.29.1-2.1
McPherson, Laura & Hayes, Bruce. 2016. Relating application frequency to morphological structure: the case of Tommo So vowel harmony. Phonology 33(1). 125–167. DOI: http://doi.org/10.1017/S0952675716000051
National Institute of Korean Language. 1999. Standard Korean dictionary.
Okumura, Mitsuo. 1955. Rendaku. Kokugogaku jiten 961–962.
Otsu, Yukio. 1980. Some aspects of Rendaku in Japanese and related problems in theoretical issues in Japanese linguistics. MIT working papers in linguistics 2. 207–236.
Park, Nayoung. 2020. Stochastic learning and well-formedness judgement in korean phonotactics: Seoul National University dissertation.
Pater, Joe. 2009. Weighted constraints in generative linguistics. Cognitive science 33(6). 999–1035. DOI: http://doi.org/10.1111/j.1551-6709.2009.01047.x
Rice, Keren. 2005. Sequential voicing, postnasal voicing, and Lyman’s Law revisited. Voicing in Japanese, 25–45.
Rosen, Eric. 2018. Rendaku database.
Sano, Shin-ichiro. 2013. Violable and inviolable OCP effects on linguistic changes: Evidence from verbal inflections in Japanese. Proceedings of FAJL 6. 145–156.
Shih, Stephanie S. 2017. Constraint conjunction in weighted probabilistic grammar. Phonology 34(2). 243–268. DOI: http://doi.org/10.1017/S0952675717000136
Shinmura, Izuru. 2008. Kōjien. Tōkyō: Iwanami shoten.
Smolensky, Paul & Prince, Alan. 1993. Optimality theory: Constraint interaction in generative grammar. Optimality Theory in phonology 3.
Stanton, Juliet. 2016. Latin -alis/aris and segmental blocking in dissimilation.
Tanaka, Yu. 2017. The sound pattern of japanese surnames: University of California, Los Angeles dissertation.
Team, R Core et al. 2013. R: A language and environment for statistical computing.
Vance, Timothy. 2007. Reduplication and the spread of Rendaku into Sino-Japanese. In Proceedings of the 31st annual meeting of kansai linguistic society, 56–64.
Vance, Timothy. 2008. Rendaku in inflected words. In Voicing in japanese, 89–104. De Gruyter Mouton.
Watanabe, Toshirō & Skrzypczak, Edmund & Snowden, Paul. 2008. Kenkyūsha new Japanese-English dictionary digital supplemented edition. Tokyo: Kenkyūsha.
Zuraw, Kie. 2010. Predicting Korean sai-siot: phonological and non-phonological factors. Handout at the 21st Japanese/Korean Linguistics Conference.
Zymet, Jesse. 2014. Distance-based decay in long-distance phonological processes. In The proceedings of the 32nd west coast conference on formal linguistics, 72–81.