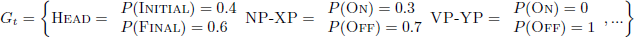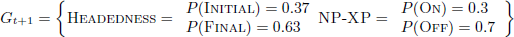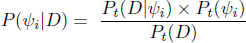1 Introduction
The source of universals and cross-linguistic generalizations has long been a central question for generative linguistics. Restrictions on Universal Grammar, computational efficiency, or processing costs are often considered as possible roots of recurrent patterns. This article investigates the possibility that universals may also arise from asymmetries in the learnability of competing syntactic patterns. Although there is a growing body of computational work modeling cross-linguistic generalizations in phonology (Boersma 2003; Heinz 2010; Pater 2012; Staubs 2014; Hughto et al. 2015; Hughto 2018; Breteler 2018; Jarosz 2019), the utility of computational models for relating learning biases to typological phenomena has yet to receive the same attention in generative syntax (notable exceptions: Kirby (1999); Smith et al. (2003); Culbertson (2010); Culbertson et al. (2012)).12 In an effort to help fill this gap, this paper presents a computational model for a simplified typology of word order, with a particular focus on the learnability of languages containing structures that violate the Final-over-Final Condition (FOFC) (Holmberg 2000; Biberauer et al. 2014; Sheehan et al. 2017: and others). The results of two learning tasks conducted here show a correlation between the learnability of a word order pattern and its frequency in the typology. The challenge presented by *FOFC languages is shown to stem from the difficulty the learner has in locating an appropriate grammar in the hypothesis space when it encounters them. This is in contrast with accounts that attribute the FOFC to a difficulty with final-over-initial tokens (such as syntactic restrictions on deriving them, or high processing cost). The rationale behind this project is as follows: Assuming a parametric model of syntax (Chomsky, 1981), a learner is faced with the challenge of deducing parameter settings, which operate over abstract syntactic structures, from the set of strings that make up their language. There are several obstacles inherent to this task. First, the learner is only exposed to a finite sample of an infinite set (poverty of the stimulus). Then, there is the problem of ambiguity, as individual strings may be compatible with multiple parameter settings (i.e. multiple grammars). Additionally, the learning problem presented by realistic language data is not always ‘smooth’ (Dresher, 1999), i.e. there is no guarantee that similar parameter settings will generate similar sets of strings. Given these challenges, it is natural to speculate that some sets of strings may be easier for a learner to relate to their corresponding parameter settings than others. Nothing in the grammar enforces that all possible parameter settings be equally easy to learn, and some syntactic patterns may therefore be more ‘learnable’ than their alternatives.
These differences in learnability have the potential to influence typology. Learning challenges which are present when looking at a small piece of language (and therefore the learning problem) are scaled up when faced with the task of acquiring a whole language. Therefore, it may be difficult to acquire a stable grammar for harder patterns given the limited time and data a human learner has. Because of this, learners may not reliably or robustly acquire the target grammars for these difficult patterns. These weak biases have the potential to be amplified into strong typological generalizations when they are transmitted across generations, as shown the Iterated Learning Framework (Kirby 1999; Smith et al. 2003; Kirby et al. 2004).
If a syntactic universal arises from this kind of learnability problem, it should be expressible as a constraint on syntactic structure, rather than strings, as structure is what parameters are generally taken to control. The FOFC provides an interesting window into the intersection of learnability and typology because it cannot be stated in terms of linear order (Biberauer et al. 2014). Instead, it constrains hidden structure (i.e. unpronounced hierarchical syntactic structures) in a way that results in a restriction on possible word orders.
The FOFC states that a head-final phrase may not immediately dominate a head-initial phrase if both are in the same extended projection (Holmberg 2000; Biberauer et al. 2014):
- (1)
- The Final-over-Final Condition (FOFC)
- *[βP [αP α ɣ ] β ] where α and ɣ are sisters and β and α are members of the same extended projection (Sheehan et al. 2017: 1).
This is based on the observation that, out of the four logically possible structures in (2), only word orders predicted by (2a–c) are commonly attested (trees from Biberauer et al. 2014: 171):
- (2)
- a.
- Head-initial (harmonic)
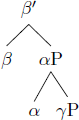
- Example: Aux Verb Object
- b.
- Head-final (harmonic)
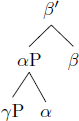
- Example: Object Verb Aux
- c.
- Initial-over-final (disharmonic)
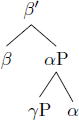
- Example: Aux Object Verb
- d.
- *Final-over-initial (disharmonic)
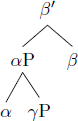
- Example: *Verb Object Aux
In addition to the FOFC, which bars structures like (2d), harmonic orders outnumber disharmonic orders (Greenberg 1963; Dryer 1992; Baker 2008). Therefore, the word-order typology can be said to exhibit two divisions in terms of frequency: harmonic orders are more common than disharmonic, and initial-over-final orders are more common than final-over-initial.
Several prior analyses of the FOFC have proposed restrictions on syntax that would prohibit final-over-initial word orders from ever being derived (that is to say, from ever being linearized)(Holmberg 2000; Roberts 2010; Sheehan 2011; 2013; Biberauer et al. 2014).3 One prominent account comes from Biberauer et al. (2014) and subsequent papers in Sheehan et al. (2017). Their analysis reduces the FOFC to the interaction of the Linear Correspondence Axiom (LCA) and restrictions on feature spreading. All syntactic structures are assumed to have an underlying head-initial configuration while other orders must be derived by movement. Harmonically head-final orders (2b) are derived via roll-up movement, where the sister of every head X moves to Spec XP. This movement is triggered by a feature ∧ that originates on the lexical head of an extended projection and spreads upwards. Initial-over-final disharmonic orders like (2c) emerge when ∧ only spreads to a subset of heads in the spine. Final-over-initial orders are ruled out because spreading of the ∧ feature is strictly local, and cannot skip over any heads in the extended projection that contains it. Therefore, no head-final phrase can be derived unless all the phrases it dominates are likewise head-final, rendering (2d) impossible.
Alone, this account has nothing to say about why harmonic orders are more common than the derivable disharmonic order (2c). Since both (2b) and (2c) must be derived via movement (and in fact (2b) requires more movement than (2c)), it is not possible to appeal to parsimony. This is addressed in Roberts (2017), who resolves this by amending the antisymmetric approach to include the idea that triggers for movement (i.e. ∧) tend to operate as a class. He sets this out as a restatement of the Cross-Categorical Harmony generalization from Hawkins (1983):
- (3)
- There is a preference for the attraction property of a functional head F∧ to generalize to other functional heads G∧, H∧… (Roberts 2017: 36)
If the generalization in (3) is true, then harmonically head-final languages are less marked than disharmonic languages because head-final harmony is produced when the ∧ feature fully generalizes. Roberts (2017) takes this to be the result of conservatism of the learner, reasoning that it is simpler for a learner to assign the ∧ feature to either all heads or no heads, rather than to a subset of heads. Roberts notes that this can be modelled using the notion of macro- and micro-parameter found in Baker (1996; 2008). Assigning the ∧ feature universally is setting a ‘macroparameter,’ while assigning it to select heads means setting multiple ‘microparameters.’ Taking Biberauer et al. (2014) and Roberts (2017), together, a split account of word order typology emerges: the prevalence of harmony is taken to be the result of asymmetries in learnability, while the FOFC is taken to be the result of immutable restrictions on possible derivations.
The model presented here takes the general idea of Roberts (2017) a step further by showing how both the preference for harmony and the FOFC may stem directly from asymmetries in learnability. Additionally, these learnability challenges need not to be built into an explicitly pre-defined learning path (i.e. with ordered macro- and micro-parameters), but may emerge automatically through the interaction of the learner with the grammar. The learning tasks were conducted using a domain-general statistical learner for parameter systems called the Expectation-Driven Parameter Learner (EDPL) (Jarosz 2015; Nazarov & Jarosz 2017).4 The EDPL was presented with the challenge of learning a word-order typology generated by a simple 4-parameter system which contained variations on the orders of {auxiliary, verb, object}. Each parameter could be set to either 1 or 0, and a setting of all four parameters constituted a language (e.g. 1000, 1100…etc.). These languages formed the hypothesis space that the learner was tasked with navigating. No explicit bias for or against a particular word order was built into the parameter system or the learner.
Using a typology generated by the 4-parameter system and a syntax described in sections 2 & 3, two learning tasks were conducted: In the first, each language in the typology had three tokens, one instance each of {auxiliary, object}, {verb, object}, {auxiliary, verb, object} (given here unordered). In the second, each language contained only the binary tokens, and the EDPL did not encounter any variant of {auxiliary, verb, object} in the training data. This 2-token task was included to investigate the role of the ternary tokens in determining how easy a word order pattern was to learn. An idea prevalent in the literature is that tokens which violate the FOFC are at fault for the phenomenon — either they are underivable, too difficult to process, unlinearizable, etc. If this is the case, then toy languages without ternary tokens would not be expected to impede learning even if their order predicted that a ternary token would violate the FOFC. The 2-token task’s inclusion was also motivated by the results of the adult learning study conducted in Culbertson et al. (2012), where participants struggled to learn artificial languages that violated Greenberg’s Universal 18 (sometimes taken as a FOFC phenomenon). Participants in that study only saw two-word tokens, and three-word tokens were not necessary for the effect to obtain.
The results of both learning tasks demonstrate a correlation between relative learnability of word order patterns and their frequency in the typology. In all tasks, the harmonic head-final order was the easiest for the EDPL to learn. In the 3-token task, the head-initial harmonic order was the next easiest, while in the 2-token task, the head-initial order and the disharmonic initial-over-final had comparable learning curves. The final-over-initial order (i.e. *FOFC) was the most difficult word order pattern for the EDPL to learn by a significant margin in both tasks, although it never failed to converge on the target pattern. Detailed results are presented in sections 5 and 6.
A closer look at the learning path of the EDPL for each word order pattern showed that the difficulty of the final-over-initial pattern is reducible to the asymmetry between leftward and rightward movement. Leftward movement creates weakly-equivalent languages for the initial-over-final pattern, which produces a more contiguous parameter space (i.e. a space where languages with similar settings produce similar-looking sets of strings). This makes the pattern easier to learn because it helps guide the learner to a suitable grammar. Leftward movement does not create weakly-equivalent languages for the marked final-over-initial pattern (*FOFC). The two languages that instantiated the final-over-initial pattern had different settings on two parameters, and this pulled the learner in two different directions, which made learning difficult.5
It is important to emphasize that these results show that it is the challenge of finding a suitable grammar that makes *FOFC languages difficult, rather than a problem specific to FOFC-violating tokens. As the results of the 2-token task demonstrate, even when the learner was never exposed to strings large enough to violate the FOFC, the final-over-initial word order pattern was the most difficult. Seeing two binary tokens that would predict a final-over-initial word order presented the learner with a comparable challenge to the 3-token task. These results parallel those in Culbertson et al. (2012).
The goal of this paper is a) to show how, under the adoption of a specific syntax and a specific learner, it may be possible to link the FOFC to learning, and b) to provide a proof of concept for the utility of learning models as a way of capturing difficult-to-explain patterns in syntactic typology. The model implemented here shows one way (and perhaps not the only way) that the FOFC can be linked to the influence that widely-observed phenomena (such as restrictions on rightward movement) have on the shape of the hypothesis space that a learner is confronted with during acquisition.
If the FOFC arises because of learnability rather than restrictions on syntax, then this may account for apparent exceptions to the FOFC reported in the literature. These include (but are not limited to) the position of sentence-final particles in Mandarin (Erlewine 2017), the availability of (S)-V-O-Aux order in Hindi (Mahajan 1990; Bhatt & Dayal 2007), and TAM particles in Amahuaca (Clem Forthcoming). The challenge that final-over-initial structures present to learning may account for their scarcity in the cross-linguistics typology. However, as the final-over-initial pattern was never completely unlearnable, exceptions to this are also accounted for. *FOFC languages may be acquirable, but the relative difficulty of acquiring them may encourage languages to shift towards other, easier patterns.
2 Syntactic assumptions
The model used focuses on {auxiliary, verb, object} tokens and discussion of syntax is framed around a clausal spine that contains just these elements. However, I assume that the relevant properties of the training data can be generalized across other instances where the FOFC is active, such as the order of CPs or PPs.
2.1 Structure of the clause
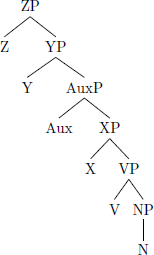
Across all examples, I assume that the structure in (4) is present even when not all elements are pronounced:
- (4)
- {ZP Z, {YP Y, {AuxP Aux, {XP X, {VP V, {NP N}}}}}
The heads Z, Y, and X are null functional elements. The specifiers for these phrases are the destination of movement used to derive various word orders in section 3. I will not speculate about the identity of these heads here, as it is not relevant for the question at hand.6
2.2 Headedness
One popular approach to linearization is the Linear Corespondance Axiom (LCA) of Kayne (1994). The LCA relies on asymmetrical c-command to determine order, stating that if a syntactic node X asymmetrically c-commands another node Y, then all terminal nodes that X dominates precede the terminal nodes that Y dominates. The result of this algorithm is that all languages should be basically head-initial, and any other surface order must be derived through movement. Unlike restrictive approaches to linearization like the LCA, I hold that phrases may be either head-final or head-initial underlyingly – heads may be linearized either to the left or right of their complements. To clarify, I assume that structures are generated with no discernible word order (i.e. as sets), and that word order is established by setting a parameter that determines whether the resulting string will be head final or head initial. This parameter linearizes structures either as entirely head initial or entirely head final, so the linearization parameter produces purely harmonic structures. This is similar in some respects to the more permissive approach to linearization put forward in Abels & Neeleman (2012) or Sheehan (2013), however in that system each phrase must be specified as either head-final or head-initial, and headedness is determined on a phrase-by-phrase basis. Unlike the Abels and Neeleman approach, I take underlying headedness to be harmonic and movement to be necessary for disharmonic patterns.
Headedness here is defined over extended projections (Grimshaw 1991). Biberauer et al. (2014) observe that the FOFC does not hold across extended projections:7 word orders like the one in (2d) are not typologically marked where β and α are, for example, a verb and a determiner. By taking headedness parameters to target extended projections, the disharmonic orders that cross them are not predicted to exhibit the FOFC. The parameter relevant for controlling headedness in the typology here is given in (5):
- (5)
- Parameter 1 (P1)
- Headedness (VP): When set to 0, each head in the extended projection of VP is linearized at the left edge of its mother. When set to 1, heads are linearized at the right edge.
This parameter is sufficient to produce the harmonic head-initial and head-final orders:
- (6)
- a.
- Head-initial: Headedness (VP) = 0
- Surface string: Aux V N
- b.
- Head-final: Headedness (VP) = 1
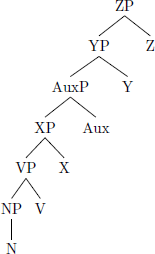
- Surface string: N V Aux
Headedness (VP) by definition cannot control the order of any components within the NP. I take this to be controlled by a Headedness (NP) parameter, not included here as it would explode the amount of weakly-equivalent languages in a way that is symmetric across the four conditions (and therefore would not affect the results).
2.3 Movement
Following Grohmann (2003; 2011); Abels (2003); Abels & Neeleman (2012), I assume that movement is sensitive to anti-locality. Specifically relevant here will be the idea that complement movement into a local specifier is insufficiently distant movement. This is contra approaches that derive the FOFC from the LCA (e.g. Biberauer et al. (2014)), which utilize anti-locality-violating roll-up movement.
The assumption of anti-locality is related to the decision to include heads X, Y, and Z in the syntactic structures used here. The specifiers of these heads act as the landing sites for movement, while anti-locality ensures that complement movement to more local specifiers need not be considered.8 The decision to include X, Y and Z, and to observe anti-locality in the training data was done in order to optimize for a small number of parameters. It may be possible to get rid of these assumptions without affecting the results, if additional parameters controlling movement were added, but I will not consider this further.
In addition to adopting anti-locality, all movement considered here is leftward, as is likewise assumed in Abels & Neeleman (2012). The asymmetry between leftward and rightward movement has been linked to the FOFC before, as in Cecchetto (2013); Zeijlstra (2016); Clem (Forthcoming). It is widely acknowledged that leftward movement is more common than rightward movement, and that rightward movement, when it occurs, is more constrained (Ross 1967). While rightward movement and specifiers are impossible in the current model, this is not a claim that rightward movement doesn’t exist as a phenomenon, just that it is constrained in such a way that is not relevant for the question at hand (for example, if its source is prosodic rather than syntactic, as proposed in Potsdam & Edmiston (2016) for Malagasy).
3 Deriving the word order typology
In this section I introduce the minimal derivations for deriving the two possible disharmonic orders from both head-final and -initial structures, along with the parameters that control them. These derivation are minimal in that they do not contain any string-vacuous movements. In the full typology there will be additional non-minimal derivations that contain string-vacuous movement – these are discussed in section 3.1. To begin, the initial-over-final pattern can be derived from an underlying head-initial structure with a single movement: NP movement into the specifier of XP, the functional projection above VP (7):
- (7)
- Head-initial → Initial-over-final
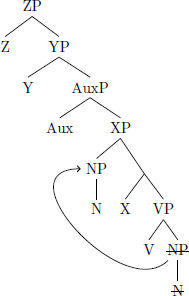
The surface order that results from the structure in (7) is Auxiliary, Noun, Verb (and therefore (7) is weakly-equivalent to (2c)). This movement is controlled by parameter 2:
- (8)
- Parameter 2 (P2)
- NP-SpecXP: When set to 0, no movement occurs. When set to 1, NP moves to the specifier of XP.
The marked final-over-initial order can also be derived from a head-initial structure using only one movement. This order obtains when the verb phrase moves into the specifier of YP, the functional projection dominating the auxiliary phrase (9):
- (9)
- Head-initial → Final-over-initial (*FOFC)
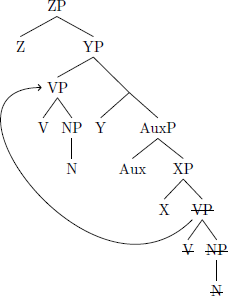
The underlying head-initial order between the verb and noun is preserved, while the auxiliary is linearized to the right, making (9) weakly-equivalent to (2d). The parameter that governs this movement is VP-SpecYP:
- (10)
- Parameter 3 (P3)
- VP-SpecYP: When set to 0, no movement occurs. When set to 1, VP moves to the specifier of YP.
In addition to these minimal derivations, both disharmonic orders can be derived from a head-final structure. However, in these cases two movements are needed instead of one. The unmarked, initial-over-final order arises when VP movement to SpecYP precedes movement of AuxP to a higher ZP phrase:
- (11)
- Head-final → Initial-over-final
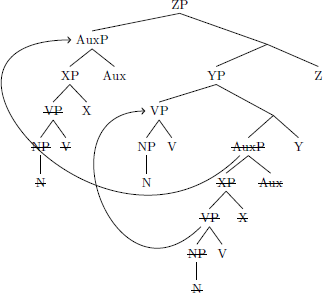
The head-final order of the noun and verb is preserved, and the auxiliary is dislocated to the left, producing Auxiliary, Noun, Verb. The first movement here is already accounted for by the VP-SpecYP parameter, and so only one additional parameter is needed:
- (12)
- Parameter 4 (P4)
- AuxP-SpecZP: When set to 0, no movement occurs. When set to 1, AuxP moves to the specifier of ZP.
Deriving a final-over-initial language from a head-final language requires no additional parameters. If NP movement to Spec XP precedes movement of VP to Spec YP, then the resulting surface order is Verb, Noun, Auxiliary (13):
- (13)
- Head-final → Final-over-initial (*FOFC)
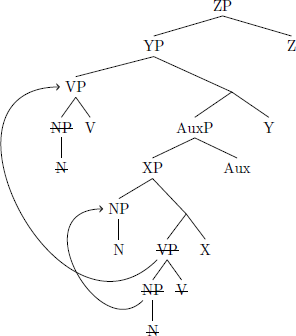
The derivations in (11) and (13) are examples of remnant movement (Müller 1997; 2002). Remnant movement was proposed in Bhatt & Dayal (2007) to account for an apparent violation of the FOFC in Hindi. This type of derivation involves movement of a complement out of its containing phrase, followed by movement of the remains of that containing phrase.
3.1 Predicted languages
Languages predicted by the parameters set out here will be henceforth named with their parameter settings. For example, the head-final language with no movement is called 1000, where the setting of each parameter appears in the order they were introduced, as in Table 1.
Languages are named by their parameter values. The order of the parameters from left to right is given in the first row. An example language name is given in the second row.
| Headedness (P1) | NP-SpecXP (P2) | VP-SpecYP (P3) | AuxP-SpecZP (P4) | |
| settings: | 1 | 0 | 0 | 0 |
The derivations in (7), (9), (11), and (13), along with the two harmonic structures in (a.) and (b.), are the set of structures giving minimal derivations for all the word orders in (2). However, they are not the only way to derive the attested patterns, as many string vacuous movements are also possible. The full set of predicted languages is given in Table 2, sorted by their surface word order pattern.
Four parameter typology sorted by surface word order.
| Initial | Final | Initial/final | Final/initial | HI +VP fronting | HF + AuxP fronting |
| 0011 | 1101 | 1011 | 1110 | 0110 | 1111 |
| 0001 | 1100 | 0111 | 0010 | ||
| 0000 | 1010 | 0101 | |||
| 1001 | 0100 | ||||
| 1000 |
As Table 2 shows, the head-initial, head-final, and initial-over-final patterns hold of a number of languages beyond the minimal derivations. This is because our parameters predict that string-vacuous movements will be possible for each of these patterns. Unlike the first three orders, the marked final-over-initial pattern (*FOFC) can only be achieved through the derivations in (9) and (13), which correspond to the languages 0010 and 1110 respectively. No vacuous movement is possible while maintaining this word order. Additionally, these parameters predict two additional word order patterns, each expressed by only a single language. I have called the first Head-initial+VP fronting. This pattern corresponds to the language 0110, and generates the word orders Aux-O, V-O, and V-Aux-O. It obtains when remnant movement of the verb phrase occurs in a head initial language. The second pattern is Head-final + AuxP fronting, and is expressed only by 1111. The word orders generated by this pattern are O-Aux, O-V, and O-Aux-V. This pattern is caused when all available movements occur in a head-final language.
4 Learning
A hypothesis about how language change might occur is as follows: at the end of the acquisition period, learners do not arrive at 100% certainty about the parameter settings of they language they have acquired. Let’s say that a stable word order pattern like Aux-V-O is acquired with 98% certainty (an arbitrary number). The result of this is a grammar that generates Aux-V-O strings 98% of the time, and non-Aux-V-O strings 2% of the time. The output of this grammar serves as the input to the next generation of learners. Since the pattern is easy to learn and dearth between Aux-V-O and non-Aux-V-O strings in the input data is so great, the second generation also acquires a relatively stable grammar. The seed of language change can be found in what happens when a learner acquires a grammar with less certainty. Say a difficult-to-learn pattern, like V-O-Aux, is acquired with only 85% certainty by the end of the critical period. The input to the next generation of learning would then be 15% non-V-O-Aux word orders. Biases like this have the potential to compound over time (Kirby 1999; Smith et al. 2003; Kirby et al. 2004) so the second generation might end up with only 84% certainty about an V-O-Aux in their language. The initial difficulty of the pattern combined with its increasing underrepresentation in the input data between generations may strengthen this bias until V-O-Aux is no longer the default word order. As a result, marked patterns like V-O-Aux may be rare because languages tend to shift away from them, while easier patterns like Aux-V-O are common because they are stable and less inclined to change.
4.1 Hidden structure
Natural language data with hierarchical structure presents language learners with a problem: they must deduce a hidden structure of each datum they encounter from its surface representation alone. The reason that this presents a challenge is because surface strings may be consistent with a number of underlying representations, and therefore a number of different parameter settings. For example, the following structures all result in a harmonic head-initial word order auxiliary, verb, noun:
- (14)
- a.
- No movement: 0000
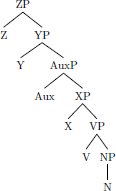
- b.
- AuxP moves: 0001
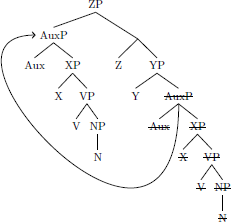
- c.
- AuxP/VP move: 0011
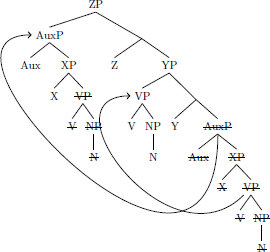
The string auxiliary, verb, noun is well-formed in languages 0000, 0001, and 0011. Movement obscures the underlying structures, and therefore the correct parameter settings.
An additional difficulty is that a single string may be derived by two or more languages that do not have similar parameter settings. In other words, the grammars that generate a particular language may not be contiguous in the parameter space. The language 0110 for instance, has more parameter settings in common with the final-over-initial language 1110 then it does with the head-initial language 0001, but produces surface strings that have more in common with head-initial languages then FOFC violators.
Ambiguity and the absence of smoothness are two factors that can make a particular pattern challenging to acquire. The harder it is to set parameters correctly, the more difficult a language is to learn. Given the number of languages even a small parameter system generates, it is difficult to intuit where and how the systems proposed to account for syntactic phenomena will present the greatest challenges to learners. To investigate what role such factors might play in the typology of word order, the learning tasks here are conducted using a computational learner as a proxy for a human learner. Although only a small number of parameters (and correspondingly small typology) will be considered, it is assumed that a much larger set of parameters are learned during acquisition.
4.2 Expectation Driven Parameter Learning (EDPL)
The Expectation-Driven Parameter Learner (EDPL) was developed in Jarosz (2015); Nazarov & Jarosz (2017); Nazarov & Jarosz (in press). The EDPL is a domain-general statistical learner for parameter systems (similar to the Naïve Parameter Learner proposed in Yang (2002)). The EDPL is able to acquire parameter settings for systems that are not smooth, and it does so gradually, offering a good approximation of human learning (and references above (Prickett et al. 2019: and references above). It is possible that results parallel to the ones presented in this paper could be obtained using another learner, such as those in Yang (2002); Goldwater et al. (2003); Gould (2015); Sakas et al. (2018), and the success demonstrated here for deriving the FOFC is not intended as an argument for the EDPL over other learners here. That being said, we will see that one property important for the results here is that the EDPL is sensitive to the contribution of individual parameter settings to errors made during learning.
The EDPL learns by testing each parameter setting and comparing the proportion of times each setting results in a match with the data. Settings that produce more matches are rewarded more in the learning update (i.e. their probability is increased). Learning is successful when the EDPL assigns a probability of 1 to a correct setting for each parameter.
The EDPL uses a probabilistic parameter grammar (PPG) framework, which is a set of independent Bernoulli distributions for each parameter (Yang 2002). The probabilities for the total setting of a parameter sum to 1, and the settings of different parameters are unrelated. An example PPG (adapted from Nazarov & Jarosz (in press) for a subset of the parameters used here) is given below:
- (15)
When a PPG is used to generate an output, its parameters are each given a categorical setting that is based on the probabilities for that parameter in the PPG. The resulting grammar is a full parameter specification (FPS). Two possible FPS based on (15) are shown in (16):
- (16)
- a.
- Sample FPS 1: Headedness = Initial, NP-XP = ON, VP-YP = Off
- probability: 0.4 × 0.3 × 1 = 0.12
- b.
- Sample FPS 2: Headedness = Final, NP-XP = Off, VP-YP = Off
- probability: 0.6 × 0.7 × 1 = 0.42
Given an unordered input, these FPS can be used to predict an output, which can be compared to an observed form (from the training data – see 4.2). For example:
- (17)
- Observed word order: N V Aux
- Unordered input: {Aux {V N}}
- Sample FPS 1:
- Sample FPS 2:
- FPS output
- Aux N V
- N V Aux
- Match with observed
- False
- True
Parameter probability distributions are updated using the Linear Reward-Penalty Scheme (LRPS: Bush & Mosteller 1951). The PPG in (15) is from a hypothetical stage where some learning has already occurred – parameter settings in the initial state have a probability of 0.5 (i.e. there is no prior bias for a particular setting of any parameter). The LRPS updates PPG probabilities with a Reward value (between 0 and 1) by which each parameter setting probability is increased or decreased. The LRPS computes a new probability for a parameter setting by taking a weighted average of the Reward value and the old probability of the parameter setting:
- (18)
- Linear Reward-Penalty Scheme (Bush & Mosteller 1951)
- Pt+1(ψi) = λ × R(ψi) + (1 - λ) × Pt(ψi)
In (18), Pt(ψi) represents the probability of a parameter setting ψi given the grammar at a time t (i.e. the current PPG). The current reward value of the parameter setting is R(ψi), where R(ψi) ∈ [0, 1], and λ is the learning rate (λ ∈ [0, 1]).
The EDPL gives each parameter setting a different reward value based on the utility of that setting in generating a match. For example, the crucial parameter setting for matching the observed word order in (17) is Headedness = Final). The fact that NP-SpecXP is set to Off is irrelevant for producing a match, as setting it to On would result in the same string once Headedness is set to Final (i.e. all else being equal, the movement it triggers is string-vacuous in a head-final language). Therefore, Headedness and NP-SpecXP should not be equally rewarded, based on this datum.
An example of how the parameter Headedness might be updated after the observation in (17) is given in (19). The learning rate is λ = 0.1, as will be the case in the learning simulations in sections 5 and 6. Taking the PPG in (15) as the current grammar, the value of the Pt (Headedness = final) is 0.6 prior to this update. Setting aside for the moment the question of how the reward is calculated, suppose the learner just observed a learning datum that strongly supports Headedness=Final and has R(ψi) = 0.9. Using these values, the headedness parameter is updated by the LRPS as follows:
- (19)
- Pt+1(Headedness = Final) = 0.1 × 0.9 + (1 – 0.1) × 0.6
- Pt+1(Headedness = Final) = 0.63
Since NP-SpecXP = Off does not contribute to the match (17), it’s Reward value will be smaller than the one in (19), and the weight of NP-SpecXP = Off will not change:
- (20)
- Pt+1(NP-SpecXP = Off) = 0.1 × 0.7 + (1 – 0.1) × 0.7
- Pt+1(NP-SpecXP = Off) = 0.7
The result of (19) and (20) is the updated PPG in (21), where an update has been made to the probability distributions of the Headedness parameter, but the the NP-SpecXP parameter weights remain unchanged:
- (21)
The sensitivity of EDPL to a parameter’s utility in producing a match with an observed datum is located in how the Reward value is calculated. The EDPL defines the Reward value for each parameter as the probability of that setting given a data point. More specifically, the Reward value of a setting is the probability of finding that setting in a successful parse of the observed data point (D) (Nazarov & Jarosz forthcoming: 13):
- (22)
- R(ψi) = P(ψi|D)
This reward value is computed using Bayes’ rule. The three quantities in (23) can then be estimated using the current grammar, and so there is no need to generate an exhaustive list of possible parses for a given datum (Nazarov & Jarosz forthcoming: 13):
- (23)
The term Pt(D|ψi) is the conditional likelihood that a given setting leads to a match. This is estimated by sampling using the production grammar. This sampling is achieved by temporarily replacing the probability of parameter setting ψi in the current grammar with 1, while leaving all other parameter settings unaltered. Then, samples are taken by repeated generation of outputs by the temporary grammar. An estimation of Pt(D|ψi) is calculated by dividing the number of matches this produces by the number of samples (25, here). Pt(ψi) is the current probability of the parameter setting, which can be ascertained by referencing probabilities in the current PPG. Pt(D) is calculated by putting the two numerator quantities into the expanded Bayes’ rule. This yields a sample-based approximation of Expectation Maximization (Dempster et al. 1977).
Reward values are calculated this way for each parameter in an FPS, one parameter at a time. Once the Reward value for a particular setting is computed, it can be plugged into the LRPS update rule in (18), which will produce an updated parameter value. Updates are calculated after each datum the learner encounters (i.e. learning is online).
4.3 Learning tasks
In both learning tasks, the learner started with unordered sets representing syntactic hierarchy and learned from training data comprised of surface strings with no constituency information. The model corresponds to a slice of learning that takes place after lexical categories (POS tags) have already been acquired. This is a common starting-point in work on syntactic parameter learning (Gibson & Wexler 1994; Yang 2002; Gould 2015; 2016; Sakas et al. 2018; Prickett et al. 2019). Similarly, the unordered constituency (section 2.1) is taken to be a part of UG. Learning is focused on the acquisition of order, and not lexical category or unordered hierarchy. The training data did not include any languages with variable word order. Additionally, the learner was only exposed to strings, and had no access to information about each datum’s hidden structure beyond hierarchy (i.e. no movement or headedness). Because of this, nothing in the data the learner sees differentiates the languages within a word order pattern, and so the learner did not make distinctions between them (see section 5).
In both tasks the learner was trained on every language for 80 passes through the data (unless otherwise noted) using a learning rate of 0.1, and averages were taken across 40 runs per language.9 Learning was deterministic (i.e. the learner acquired a single parameter setting for each pattern) in all cases except one (the 3-token final-over-initial order; section 5.4), and averages were taken across runs to reduce noise. In the 3-token task, there were three data points per language an {Auxiliary, Object} sequence, a {Verb, Object} sequence, and an {Auxiliary, Verb, Object} sequence. The 3-token typology is given in Table 3.
Word order patterns and their languages in the 3-token task. The first row lists each word-order pattern, and the second gives each parameter setting that will achieve it. The first column shows the unordered inputs, while all other cells give the correct output for each language/input combination; these are the forms that made up the training data.
| HI | HF | I-over-F | F-over-I | HI+F | HF+F | |
| 0011, 0001 0000 |
1101, 1100, 1010 1001, 1000 |
1011, 0111 0101, 0100 |
1110, 0010 | 0110 | 1111 | |
| {Aux{O}} | Aux-O | O-Aux | Aux-O | O-Aux | Aux-O | O-Aux |
| {V{O}} | V-O | O-V | O-V | V-O | V-O | O-V |
| {Aux{V{O}}} | Aux-V-O | O-V-Aux | Aux-O-V | V-O-Aux | V-Aux-O | O-Aux-V |
In the second task, there are only two data points per language, an {Auxiliary, Object} sequence, and a {Verb, Object} sequence. No language in this training data included the ternary {Auxiliary, Verb, Object} sequence. The 2-token typology is given in Table 4.
Word order patterns and their languages in the 2-token task.
| Head-initial | Head-final | Initial-over-final | Final-over-initial | |
| 0011, 0001 0000, 0110 |
1101, 1100, 1010 1001, 1000, 1111 |
1011, 0111 0101, 0100 |
1110, 0010 | |
| {Aux{O}} | Aux-O | O-Aux | Aux-O | O-Aux |
| {V{O}} | V-O | O-V | O-V | V-O |
Since the only thing that distinguishes the +fronting word order patterns from the harmonic patterns is the ternary token, these languages are absorbed into the harmonic word order patterns in the 2-token task.
5 Results for the 3-token task
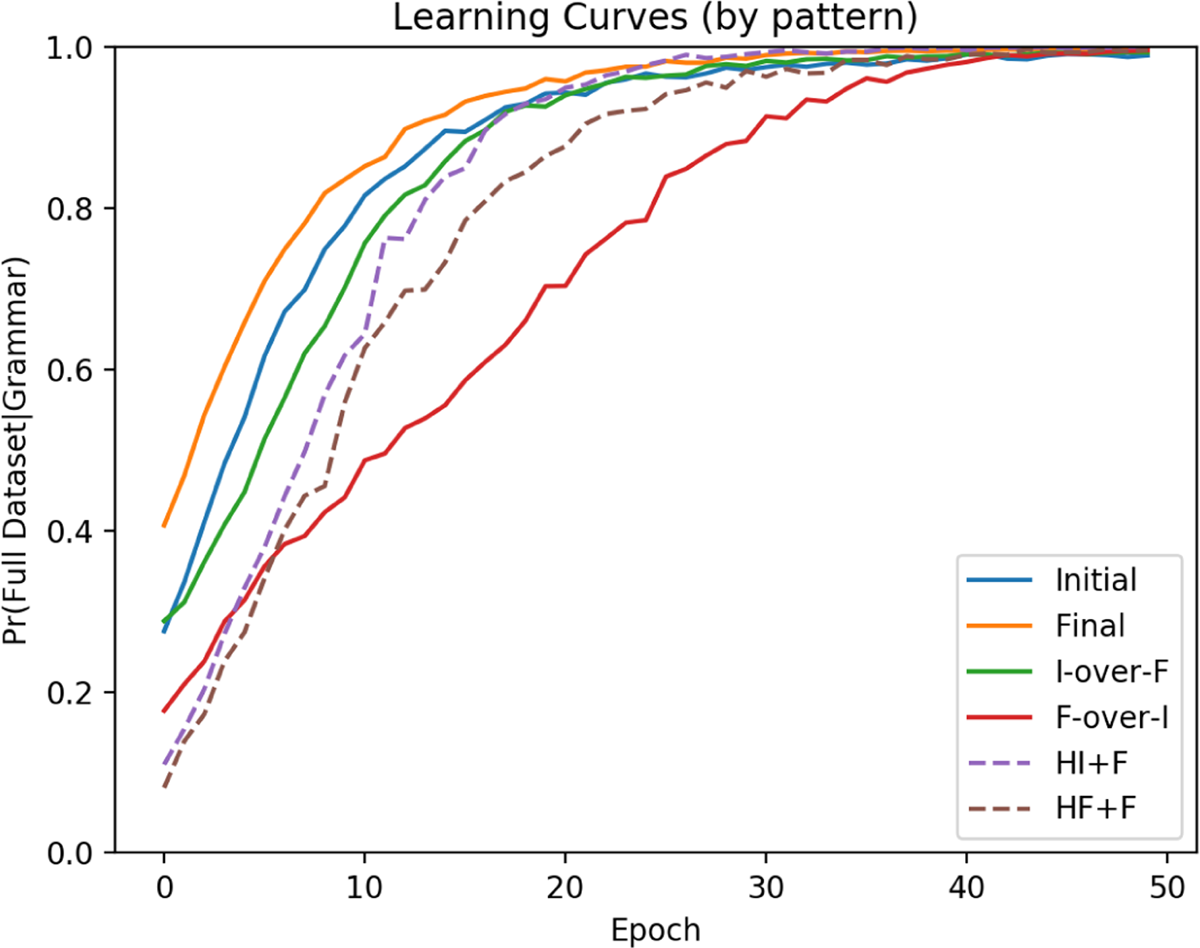
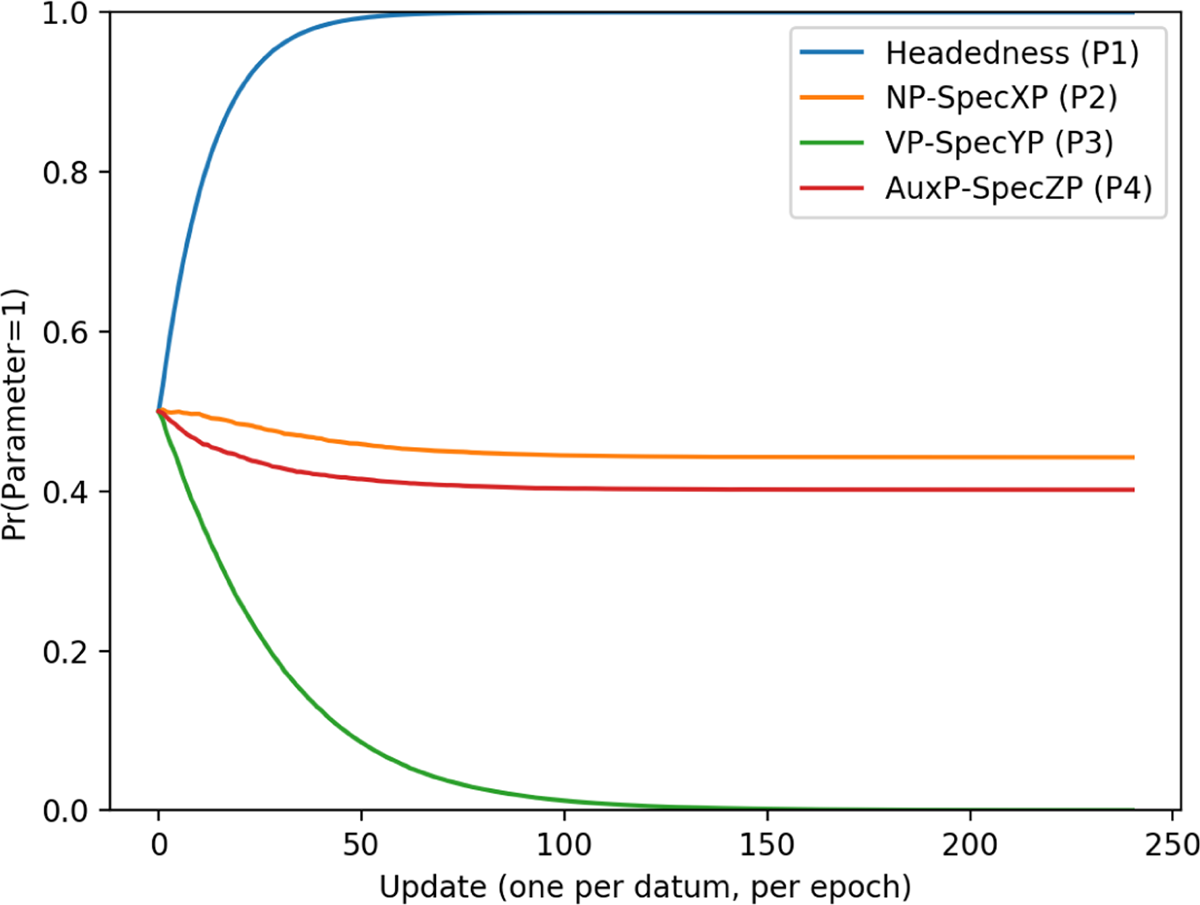
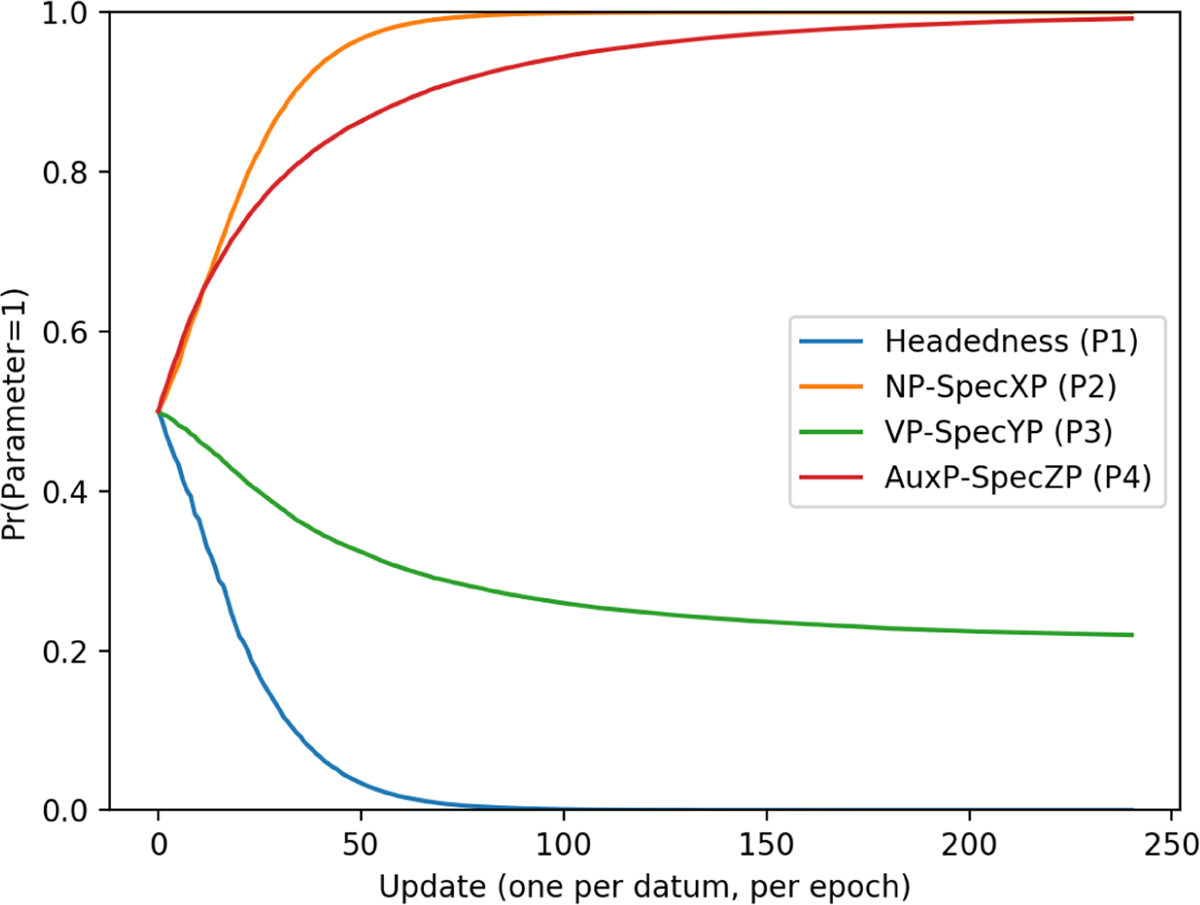
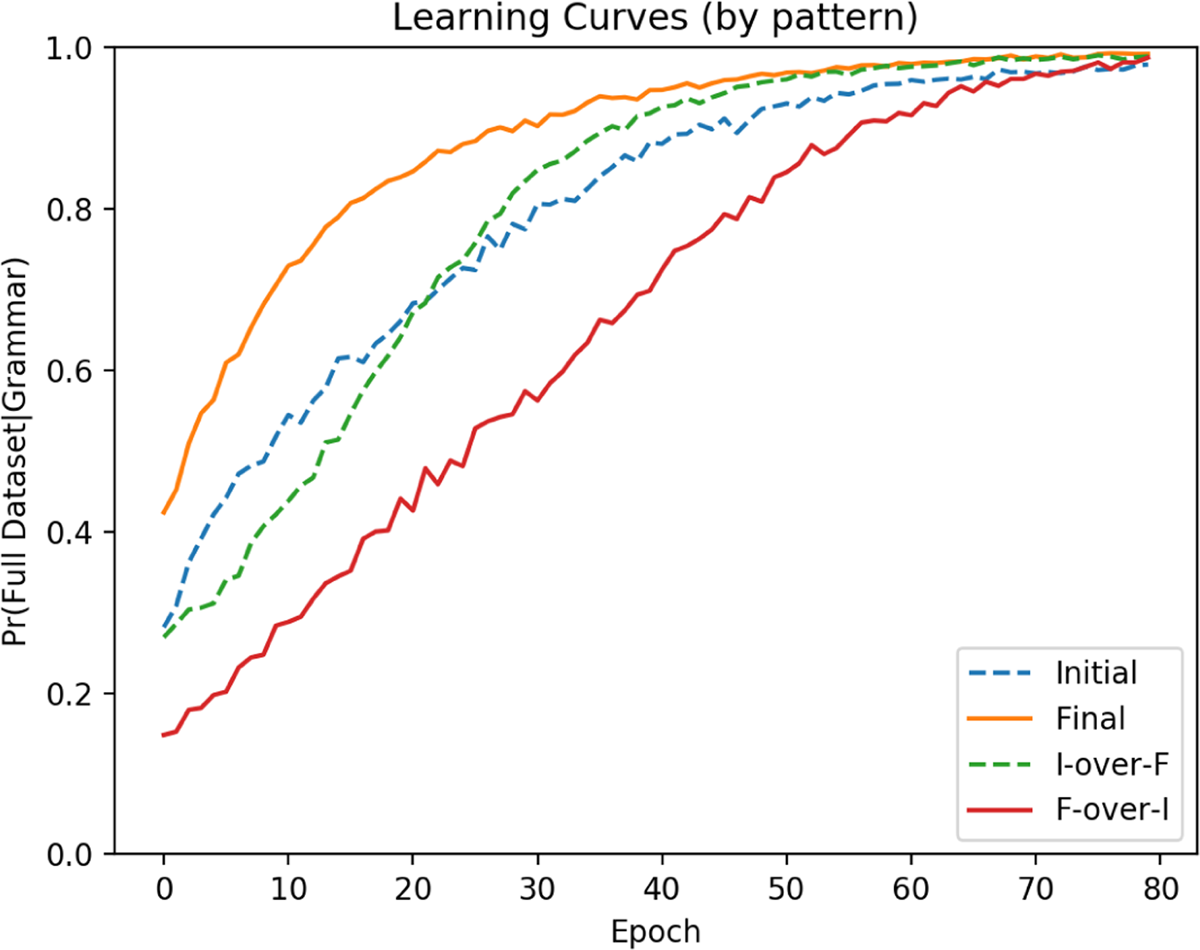
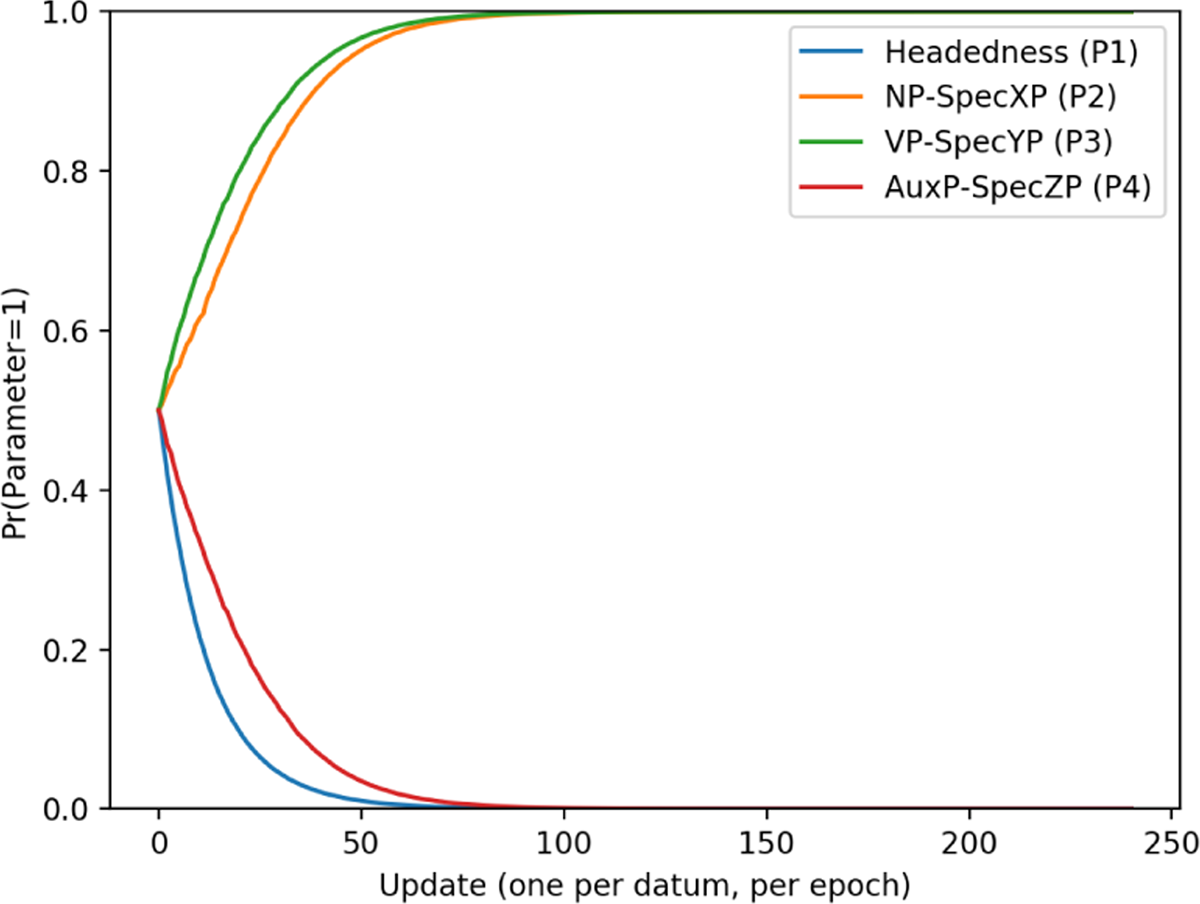
As noted in section 4.3, the learner did not differentiate between weakly equivalent languages. Because weakly equivalent languages were undistinguishable in the training data, the learner always converged on the same parameter settings for each. Therefore, the learning curves for the 3-token task are given by pattern (as opposed to individual language) in Figure 1.
The learner reached a high degree of proficiency for all languages in the 3-token task by 50 passes through the data (called ‘epochs’ here). The EDPL is different from a human learner in many respects, but crucially in that there is no cap on acquisition in terms of time or amount of data. Because of this, the EDPL eventually acquired all word orders with 100% certainty (all lines converge at 1). Therefore the learner’s ultimate success is not a good measure of a word order’s difficulty here. Instead, the measure of difficulty is the amount of time and data it takes for a learner to reach a high accuracy; that is to say, the measure of difficulty is the steepness of the learning curve, rather than its destination. Curve steepness can be measured by looking at how long it takes the EDPL to reach high accuracy for each word order pattern. I have chosen 80% here (0.8) for clarity. For example, the learner reaches 80% accuracy for the harmonic head-final pattern by about 7 passes through the data. The final-over-initial pattern, on the other hand, takes the learner over 20 passes through the data to reach 80%. More than twice the amount of data was needed for the learner to achieve high accuracy (80%) on the final-over-initial pattern than for the harmonic head-final pattern. So if a human learners have, for example, only 20 epochs in which to learn, they can acquire all word orders to 80% accuracy except for the Final-over-Initial order. Based on this, we can say that the final-over-initial is ‘harder’ to learn than any other pattern.
According to this metric, the easiest language pattern for the EDPL to learn (i.e. the one with the steepest learning curve) was the harmonic head-final pattern (languages 1101, 1100, 1010, 1001, 1000). The second easiest pattern was harmonic head-initial (languages 0011, 0001, 0000), which took about 9 passes through the data for the learner to achieve 80% accuracy. This was closely followed by the disharmonic initial-over-final pattern (languages 1111, 1011, 0111, 0101, 0100), which took 11 passes through the data. These are the three word order patterns that are frequently attested. The learner next converged on settings for the two outlier languages included as a prediction of the particular parameters used here. These are the head-initial with VP-fronting, and the head-final with AuxP fronting pattern, both of which corresponded to only one language each, and which trailed behind the other patterns in part because they have a relatively low starting probability (see section A.1 for further details). It took the learner 13 and 15 passes through the data respectively to reach 80% accuracy on these patterns. The pattern with the flattest learning curve, and therefore the most difficult to learn, was the final-over-initial pattern (20 passes through the data to reach 80%). Importantly, this is the word order pattern which violates the Final-over-Final Constraint.
The particular settings that the learner converged on for each of the four attested patterns are discussed in sections 5.1–5.4, along with an examination of why the learner arrived at each setting, and how that relates to the relative difficulty of each language. Data from the unattested patterns (Head-initial + VP fronting & Head-final + AuxP fronting) can be found in appendix A.1.
5.1 Harmonic head-final (3-token)
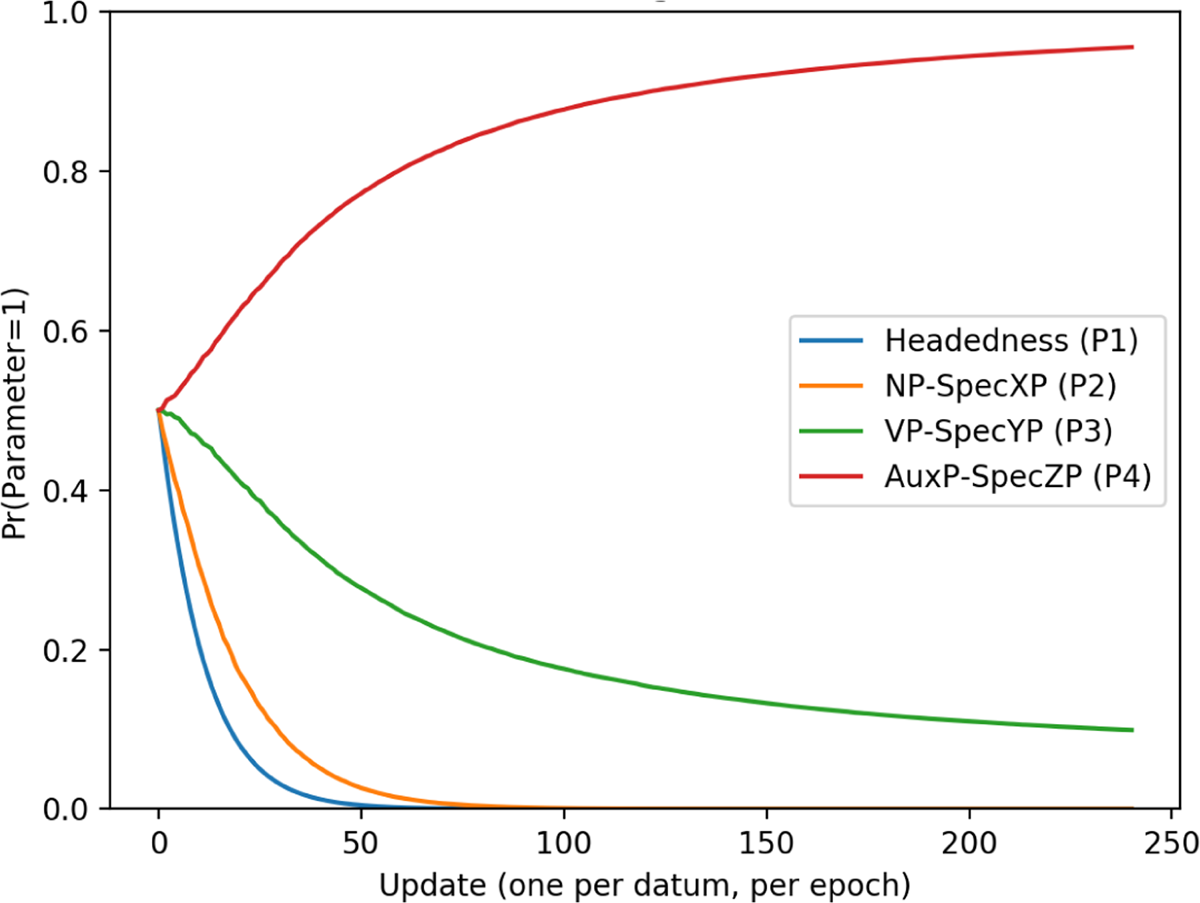
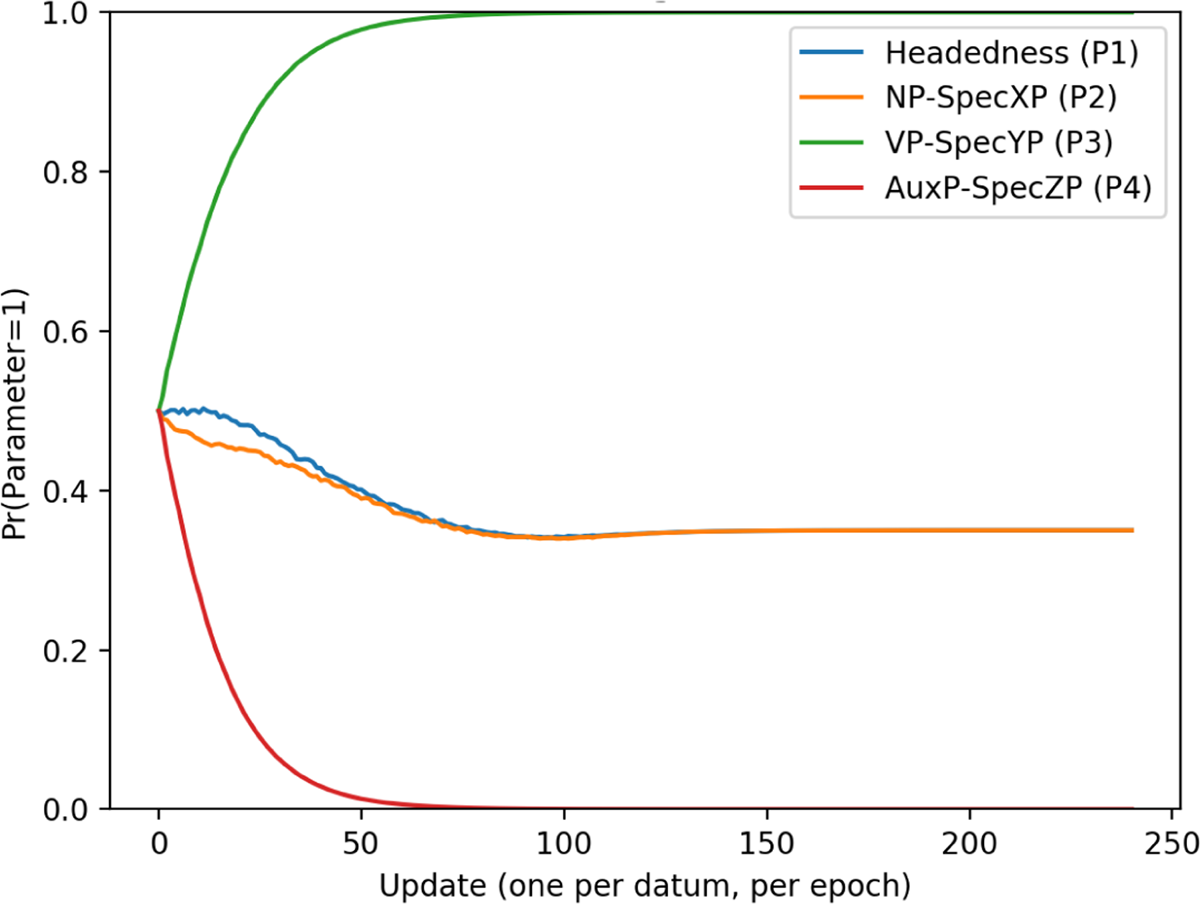
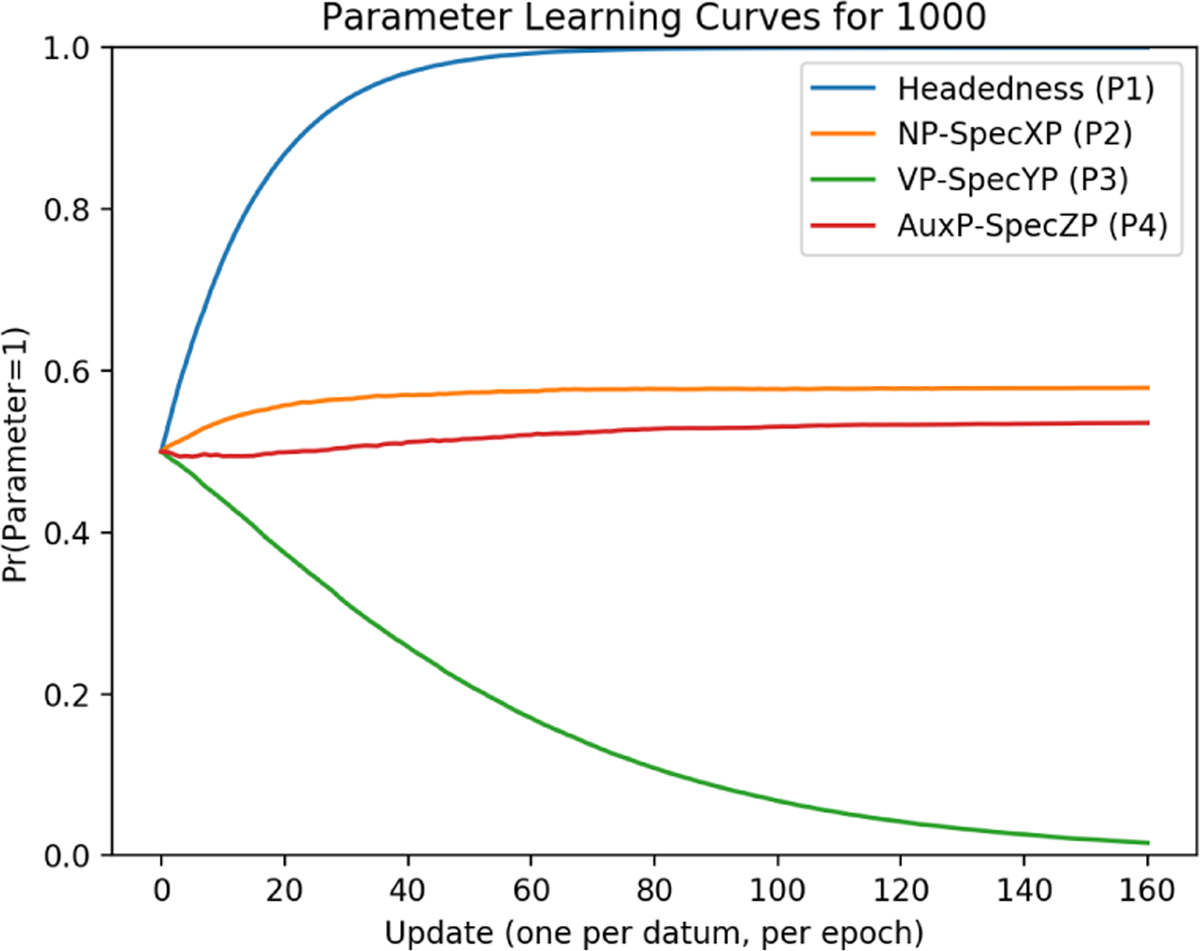
Parameter learning curves for languages with a harmonic head-final surface order can be seen in Figure 2. As with the by-language and by-pattern curves, these are taken as an average over 40 reps. The parameter values in this particular graph are for language 1000, but as noted in section 5, the same parameter values are consistently learned for all languages with a single surface pattern.
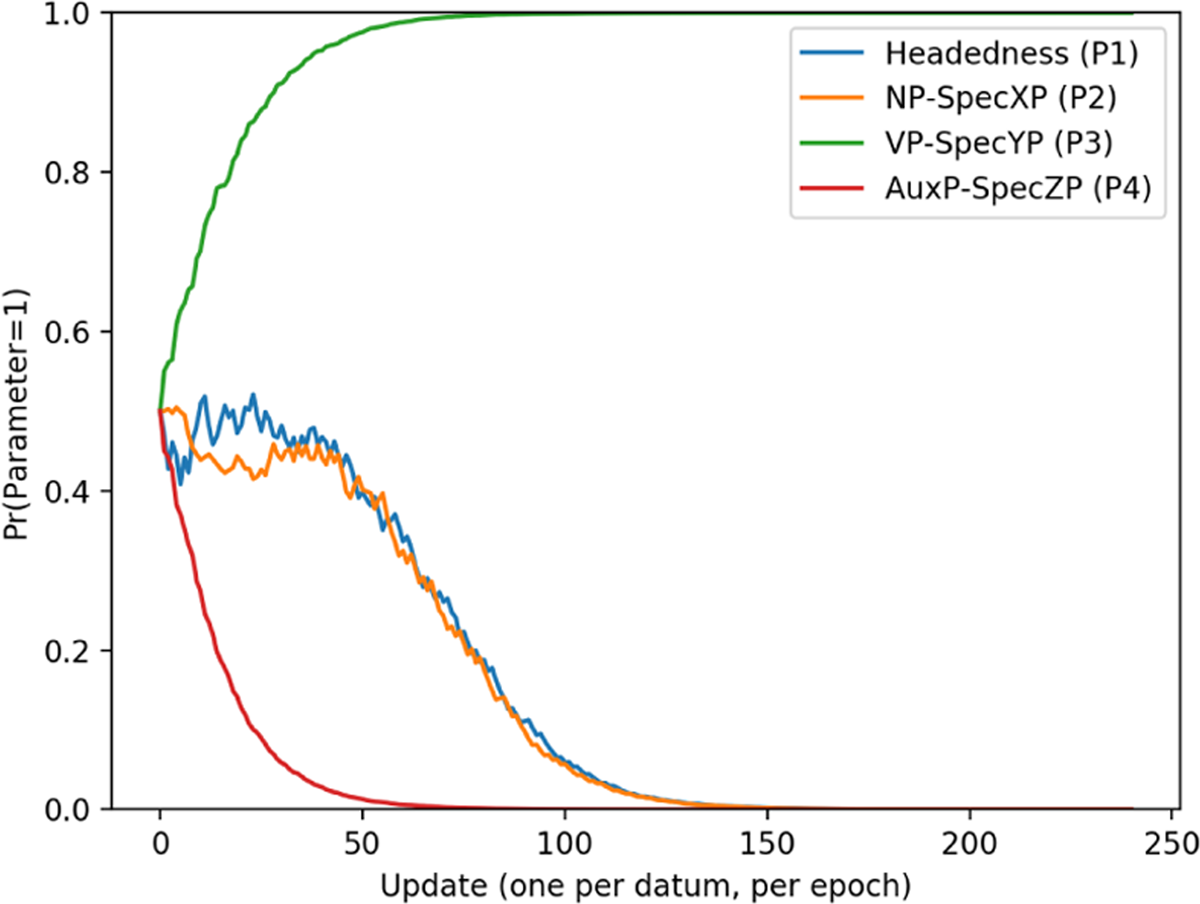
The first parameter to be learned is Headedness (P1) This parameter is set to 1 by about 60 updates. At about 120 updates, VP-SpecYP (P3) reaches 0. After this, the learner does not converge on a value for the parameters NP-SpecXP (P2) or AuxP-SpecZP (P4). Given that harmonic head-final languages were the easiest to acquire (as demonstrated in Figure 1), this suggests that the settings of these parameters does not matter for the purposes of acquiring head-final languages, at least once the first and third parameters are set.10 This is confirmed by looking at parameter curves for a single run (analogous to a single learner; Figure 3).
What this means is that the learner can pick any setting for P2 and P4, and any combination of those two settings, and still produce the correct output. A closer look at the data confirms this. Table 5 shows to what extent the individual tokens in training data for the harmonic head-final languages are correlated with a setting of one for each individual parameter.
Preference of head-final tokens for 1.
| Inputs | Headedness (P1) | NP→XP (P2) | VP→YP (P3) | AuxP→ZP (P4) |
| O-V | 0.7 | 0.6 | 0.4 | 0.6 |
| O-Aux | 0.87 | 0.5 | 0.5 | 0.37 |
| O-V-Aux | 1 | 0.4 | 0.2 | 0.4 |
This is calculated by looking at how many times a particular token appears in a language with that parameter set to one (across all language patterns), and dividing that number by the total number of the languages the token occurs in. For example, the token O-V occurs in 10 languages (five head-final, five initial-over-final). In seven of these languages, the first parameter is set to 1. Therefore, the extent to which O-V favors setting P1 to 1 is .7.
The easiest parameter for the learner to set is Headedness (P1) because the ternary token disambiguously prefers 1 (i.e. O-V-Aux never appears in a language where P1=0). VP-SpecYP (P3) is also relatively easy to set, because all three tokens push the learner towards a 0 setting, although none are disambiguating. The tokens are not united in which direction they push the learner for P2 and P4. O-Aux and O-V-Aux push the learner towards 0, while O-V pushes the learner towards 1. One might anticipate that in this case, both parameters will eventually be set to 0, since the majority of tokens favor this setting. However, it is important to note that the preferences in Table 5 are inherent to the training data and only hold prior to any learning. Once some learning has occurred, certain languages become more heavily weighted than others, and the parameter settings most likely to produce a match may change. For example, once two parameters have been set for the head-final data (i.e. P1 and P3), this helps eliminate some potential ‘nearby’ languages which are otherwise compatible with the training data:
- (24)
- Head-final languages
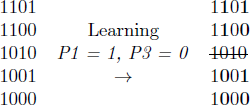
Because of this, the likelihood of the learner producing the correct outputs with particular settings of the remaining parameters changes. In this case, once P1 has been set to 1 and P3 has been set to 0, the settings of P2 and P4 no longer matter – every combination of settings will product a match with the training data. The learner therefore need not select a single setting for these two parameters in order to successfully learn a harmonic head-final language.
In summary: despite ambiguity in the data (i.e. many parameter settings compatible with the observed tokens), the harmonic head-final pattern is relatively easy for the learner because only two parameters need to be set for it to be successful, and one of these parameters is disambiguated by the ternary token. The language ultimately learned for the head-final pattern was 1 ~0~, where ~ indicates a parameter which did not need to be consistently set to either 1 or 0. To clarify, this means that the grammar the learner acquired was (covertly) stochastic. Whenever the learner goes to use a ~ setting, it picks either 1 or 0 at random, and since any setting produces the right output, there is no variation in the tokens it produces (i.e. no surface evidence that the grammar is stochastic).
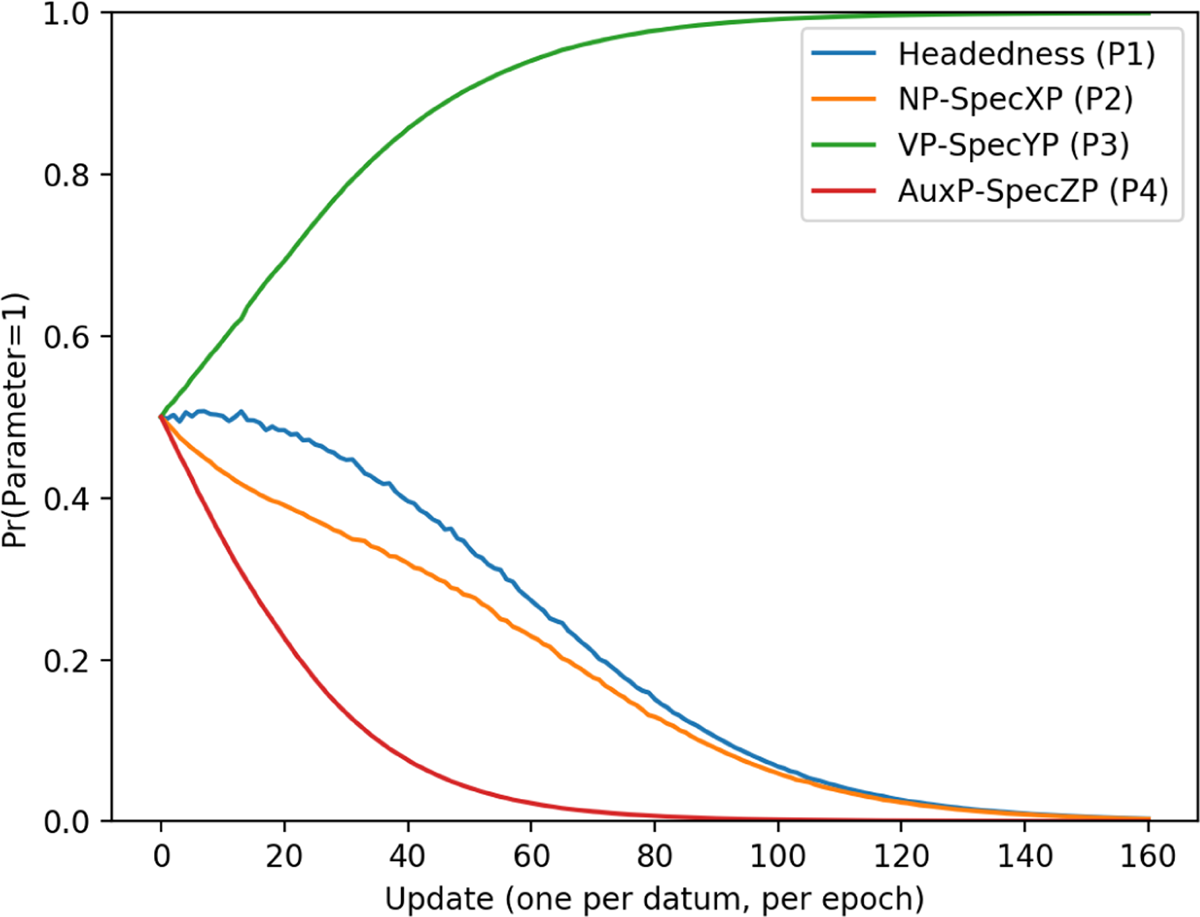
5.2 Harmonic head-initial (3-token)
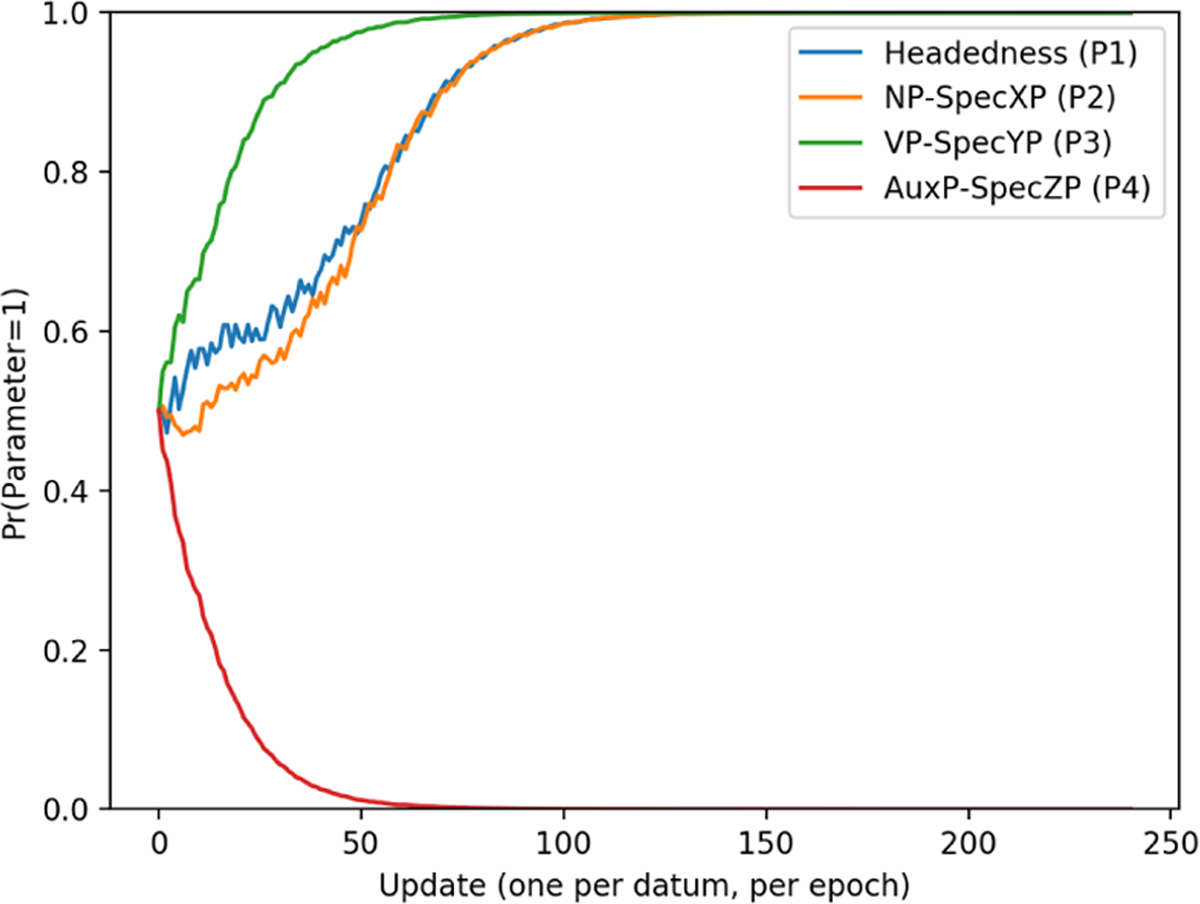
The harmonic head-initial pattern was the second easiest language (i.e. had the second steepest curve). The average parameter curves are given in Figure 4.
Here the learner quickly converges on a 0 setting for Headedness (P1) and NP-SpecXP (P2). For Headedness, this happens by about 50 updates, followed by NP-SpecXP at about 80. The other two parameters are much slower, with AuxP-SpecZP(P4) eventually converging on 1, and VP-SpecYP(P3) plateauing. In fact, although the learner gets very close to converging very early on, it actually takes around 500 updates for the AuxP-SpecZP(P4) to be completely set to 1. This can be seen in Figure 5.
Although it takes approximately 500 updates for P4 to be set to 1, the learner is close enough by around 150 updates that the fact that it hasn’t completely converged is not easily discernible from Figure 1. Again, looking more closely at the data sheds light on why the parameters are learned in this order and at this rate. The correlation of each head-initial token with parameter settings of 1 is given in Table 6.
Preference of head-initial tokens for 1.
| Inputs | Headedness (P1) | NP→XP (P2) | VP→YP (P3) | AuxP→ZP (P4) |
| V-O | 0.17 | 0.33 | 0.67 | 0.33 |
| Aux-O | 0.13 | 0.5 | 0.5 | 0.63 |
| Aux-V-O | 0 | 0 | 0.33 | 0.67 |
The ternary token disambiguates the first two parameters, and this accounts for why they are set quickly. P2 takes slightly longer to set than P1 on account of the minority report of the Aux-O token which, unlike V-O and Aux-V-O, pushes the learning towards 1 instead of 0 for P2. After the first two parameters are set, the following languages are possible:
- (25)
- Head-initial:
- 0011
- 0001
- 0000
- Final-over-initial:
- 0010
Unlike in the head-final case, setting two parameters is not sufficient for learning the head-initial pattern, as there is a nearby language (0010) which will not produce the right output. This “attractive neighbor” needs to be rejected before learning can be successful, and so additional parameters must be set. Specifically one additional parameter needs to be set. The two possible solutions for the learner are to a) set P3 to 0, in which case the setting of P4 does not matter, or b) to set P4 to 1, in which case the setting of P3 does not matter. The reason that P4 is set first is because 2/3 of the head-initial tokens prefer setting this parameter to 1, so that setting gets an initial boost before other learning occurs (as can be seen in (27)). The head-initial tokens do not push P3 towards 0 as strongly, and so P3 plateaus after P4 is set.
As noted above, despite a relatively steep learning curve, the learner is fairly slow to completely converge on parameter settings for this word order pattern. The reason for this is that, before P4 completely converges (with P1 & 2 already set), the learner is already very accurate. Given the languages that are highly weighted at that point (i.e. the languages in 27), the learner has a 75% chance of correctly producing Aux-V-O and Aux-O tokens, and 100% chance on V-O.
In combination with how close P4 & P3 have been pushed towards 1 and 0 respectively, this means that the learner is hardly ever wrong. Responsibility for matches is therefore diffused between both parameter settings, and it takes a long time for one to become more highly weighted than the other. This is one reason why the time it takes for the learner to fully set parameters for a language pattern is not used here as a complete measure of how learnable that pattern is. The head-initial pattern has a relatively steep learning curve, and the learner quickly achieves high accuracy, despite taking many updates to totally converge on all parameter settings.
Ultimately, the parameter values learned for the harmonic head-initial pattern were 00~1. Although the first two parameter settings are disambiguated by the ternary form, this pattern was still a bit more difficult than the head-final harmonic pattern. The reason for this is that more parameters needed to be set correctly in order for learning to be successful. The head-initial pattern requires the correct setting of three parameters, while the head-final pattern only required two.
5.3 Disharmonic initial-over-final (3-token)
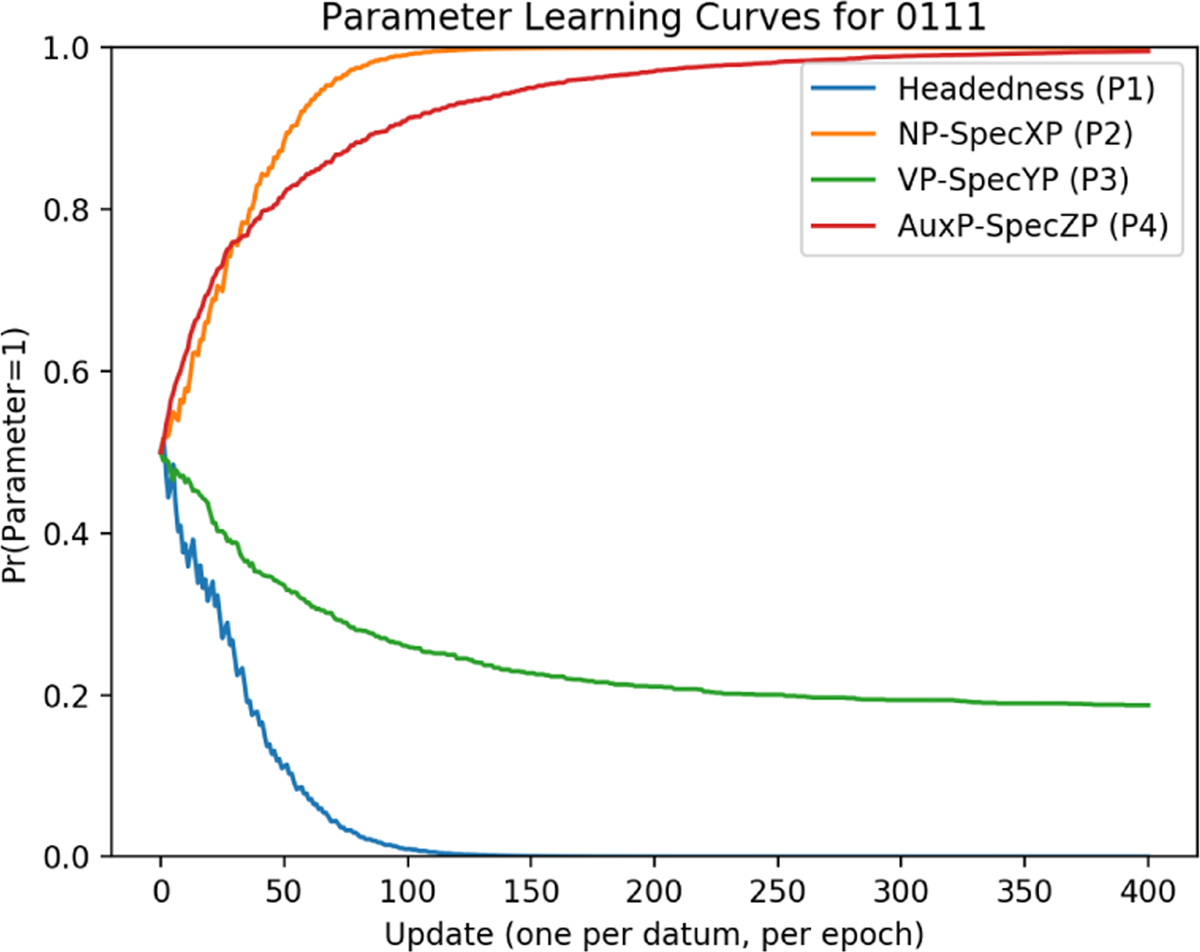
The initial-over-final pattern (a.k.a the unmarked disharmonic pattern) was only slightly harder to learn than the two harmonic patterns, as in Figure 1. The parameter curves for initial-over-final can be seen in Figure 6.
AuxP-SpecZP (P4) and NP-SpecXP (P2) are both set by about 90 updates. Headedness (P1) is the next to be set, more slowly, to 0, and at that point VP-SpecYP (P3) plateaus. Before any learning occurs, the preference of tokens for setting each parameter to 1 are in Table 7.
Preference of initial-over-final tokens for 1.
| Inputs | Headedness (P1) | NP→XP (P2) | VP→YP (P3) | AuxP→ZP (P4) |
| O-V | 0.7 | 0.6 | 0.4 | 0.6 |
| Aux-O | 0.12 | 0.5 | 0.5 | 0.6 |
| Aux-O-V | 0.25 | 0.75 | 0.5 | 0.75 |
Unlike the harmonic patterns, the initial-over-final pattern has no parameter setting that is completely disambiguated by one or more tokens. However, all three tokens push the learner to a 1 setting for P4, and 2/3 tokens push the learner towards 1 for P2, while the third is at chance. Both of these parameters are initially pushed towards one. At about 20 updates, the curves for P2 and P4 diverge, and P2 is set first, despite the fact that all tokens initially push P4 towards 1. To determine the source of this divergence, it is necessary to look at the approximate weight of each parameter at 20 updates. Table 8 gives the (approximate) probability that each parameter setting is 1 at 20 updates.
Probability of P=1 at 20 updates.
| P1 | P2 | P3 | P4 |
| 0.35 | 0.7 | 0.45 | 0.7 |
Based on this, the approximate probability of each possible initial-over-final language at that point is as in Table 9.
Weights at 20 updates.
| 1011 | 0111 | 0101 | 0100 |
| 0.033 | 0.143 | 0.175 | 0.075 |
The combined weight of initial-over-final languages where P2 is set to 1 (0.4) has at this point become greater than the combined weight of languages where P4 is set to 1 (0.35). As learning goes forward this gets exacerbated, giving P2 a boost towards 1 that results in it being set before P4. Therefore, P1 and P2 are the first parameters to be correctly set. As in the head-initial pattern, the languages remaining after the first two parameters are set are not all initial-over-final, but include a neighbouring language:
- (26)
- Initial-over-final:
- 0101
- 0111
- 0100
- AuxP Fronting:
- 0110
As in the head-initial case, there are now two possible solutions for the learner to set the final parameters. P3 could be set to 0, in which case the setting of P4 would not matter, or P4 could be set to 1, in which case the setting of P3 no longer matters. P4 is set first, because it was pushed towards 1 by all tokens initially, unlike P3, which was only pushed towards zero by one token.
The parameter settings the learner converges on for the initial-over-final pattern are 01~1. First P1 & P2 are set, and then P4 is pushed slowly towards 1. Once P4 is set, the setting of P3 no longer matters for the pattern to be successfully learned. This is similar to the way the head-initial pattern was learned, with three parameter settings being necessary for successful learning. However, unlike the head-initial language, no parameters are disambiguated by the ternary form for the initial-over-final pattern.
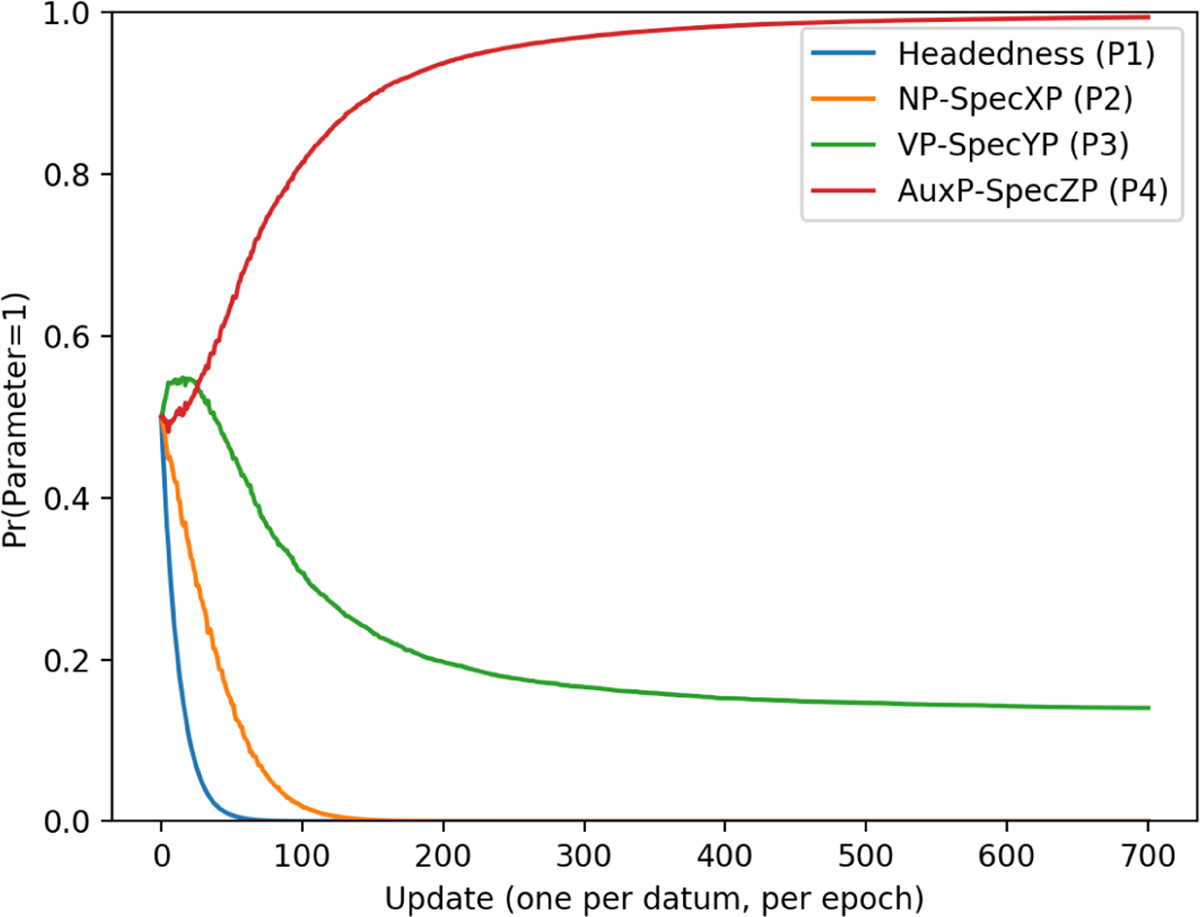
5.4 Disharmonic final-over-initial (marked) (3-token)
The final-over-initial pattern (i.e. the marked disharmonic order) was the most difficult for the learner to successfully acquire. Average parameter learning curves for the example language 0010 are given in Figure 7.
The first parameter to be learned was AuxP-SpecZP (P4), which was set to 0 by approximately 60 updates. This was followed by VP-SpecYP (P3) being completely set to 1 by 80 updates. After these parameters are successfully valued, Headedness (P1) and NP-SpecXP (P2) appear to drift slightly towards 0 before appearing to plateau. Unlike in previous cases, however, no plateauing actually occurs for any parameters in the final-over-initial pattern. This becomes evident when looking at parameter curves for individual reps.
Figures 8 and 9 show that what is actually happening in Figure 7 is that the learner is not consistently landing on one parameter setting for this word order pattern. Instead, It converges on 1110 on just under 40% of runs, and on 0010 for the remaining (approx.) 60%. Because figure 7 shows curves over an average of reps, this gives the illusion of plateauing.
Looking at the starting preference of the final-over-initial tokens for setting parameters to 1, it is easy to see why parameters 3 and 4 are easy for the learner to set. Both of these parameters are disambiguated by the ternary form, as seen in Table 10.
Preference of final-over-initial tokens for 1.
| Inputs | Headedness (P1) | NP→XP (P2) | VP→YP (P3) | AuxP→ZP (P4) |
| V-O | 0.17 | 0.33 | 0.67 | 0.33 |
| O-Aux | 0.87 | 0.5 | 0.5 | 0.37 |
| V-O-Aux | 0.5 | 0.5 | 1 | 0 |
V-O-Aux is only a possible output if P3 is set to 1 and P4 to 0, it does not occur in any languages that deviate from these settings. Once these two parameters are set correctly, the following languages remain:
- (27)
- Final-over-initial:
- 0010
- 1110
- Head-final:
- 1010
- Head-initial + fronting:
- 0110
There are several sources of difficulty for the learner here. First, setting one additional parameter after P3 and P4 are set correctly will not make the final parameter setting irrelevant. All four parameters must be correctly set for the final-over-initial pattern to be learned. This contrasts with the other word-order patterns, which only required two or three parameters to be set before the language could be successfully learned. This is because the final-over-initial order has more nearby competitors than the other word order patterns, which had at most one neighbour to rule out.
A second problem is that the learner is not strongly pushed towards a particular setting on the first two parameters. For the first parameter, there is no obvious starting preference in the final-over-initial languages for a setting of either 1 or 0, so the learner is initially pulled in different directions. The second parameter is slightly more likely to have a setting of 0, and the P2 parameter curve does initially drift towards 0 in Figure 7, but this effect is not strong enough to consistently cause the learner to pick a 0010 setting. Adding to this problem is the fact that the settings of the first two parameters are dependent. For example, setting P1 to 0 obliges the learner to also set P2 to 0 in order to be successful. This means that, in addition to being pulled in different directions for the individual settings of P1 and P2, the learner can be pulled in different directions by a ‘disagreement’ between P1 and P2.
Something notable about the parameter curves for the final-over-initial language is that the source of difficulty when learning this pattern does not appear to come from how long it takes the individual parameters to be set. Compare, for example, the relative number of updates for all parameters to be learned in Figure 6 vs. Figure 7. The difference here is that, although the initial-over-final and head-initial took longer for all parameters to be set, the learner quickly arrived at a point where it was choosing between languages which always or nearly always resulted in the correct outputs. On the other hand, while it took fewer updates for all the final-over-initial parameters to be set, the learner was much more likely to be wrong at each stage of learning, as the ratio of correct languages to nearby languages is much smaller for the final-over-initial order than for the other patterns. This is why the final-over-initial pattern has the flattest learning curve in Figure 1, and is the most difficult for the learner to acquire.
6 Results for the 2-token task
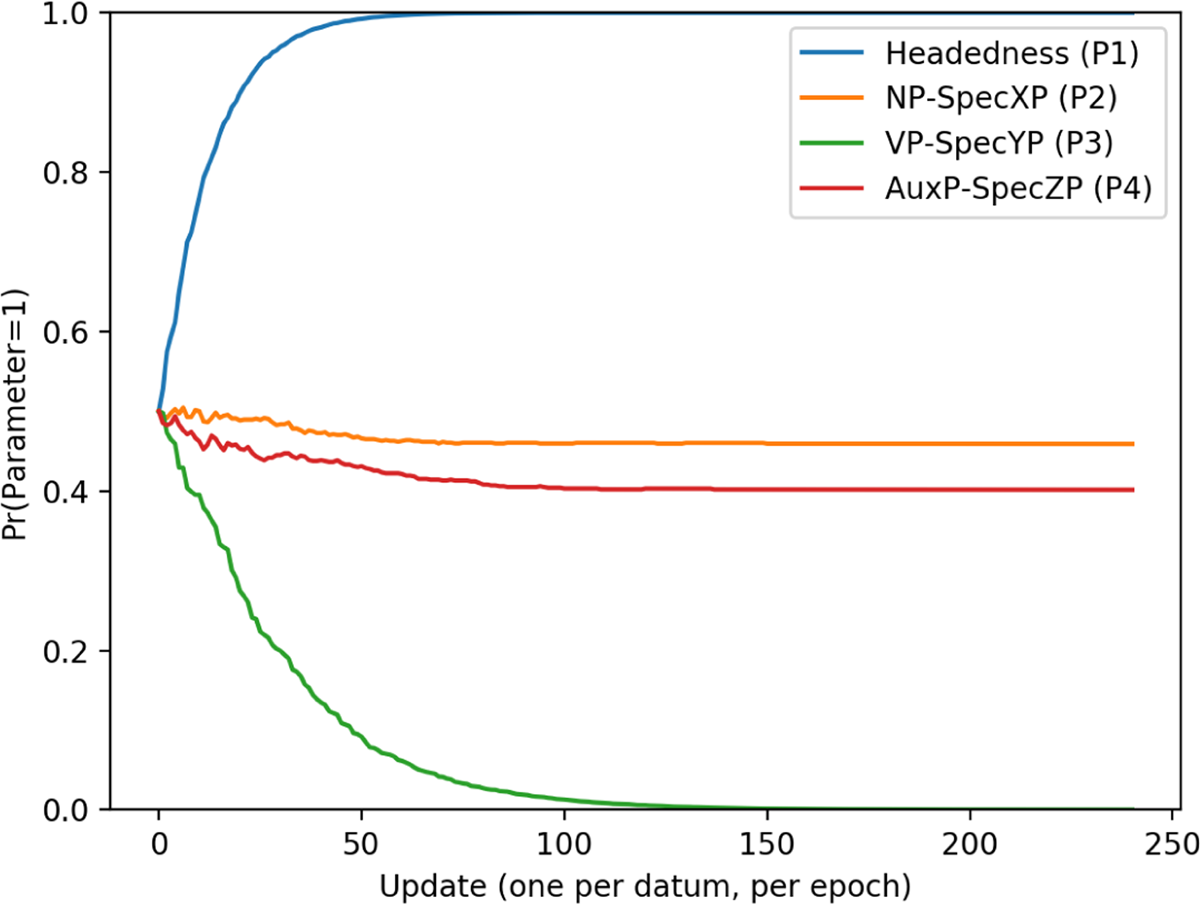
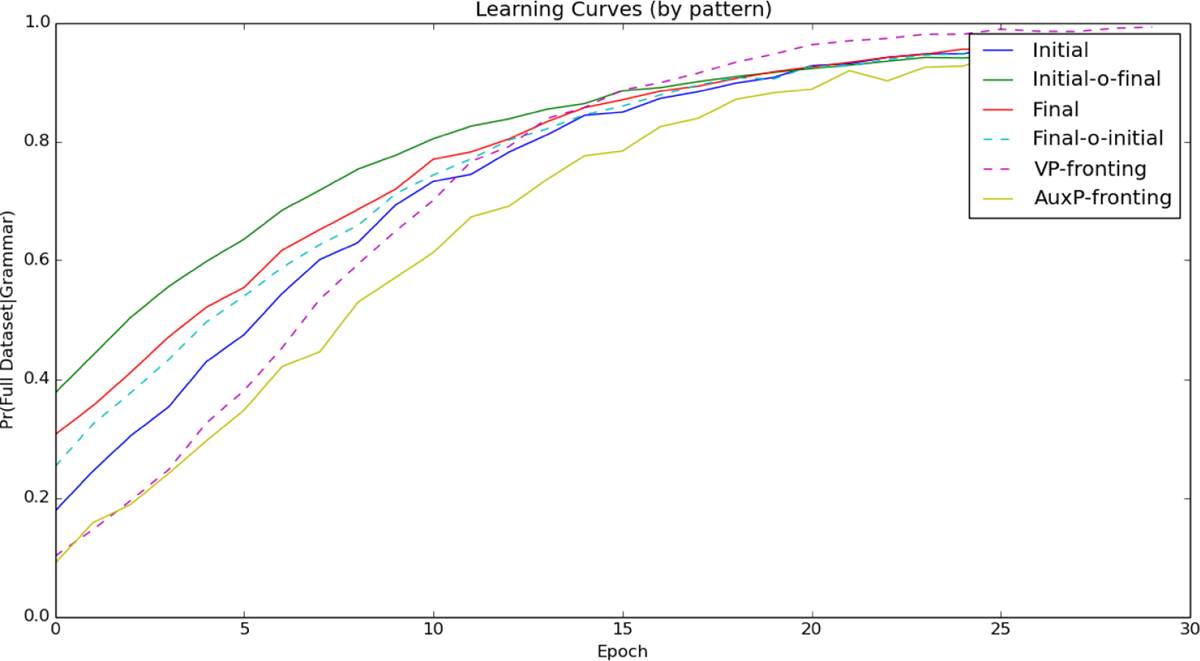
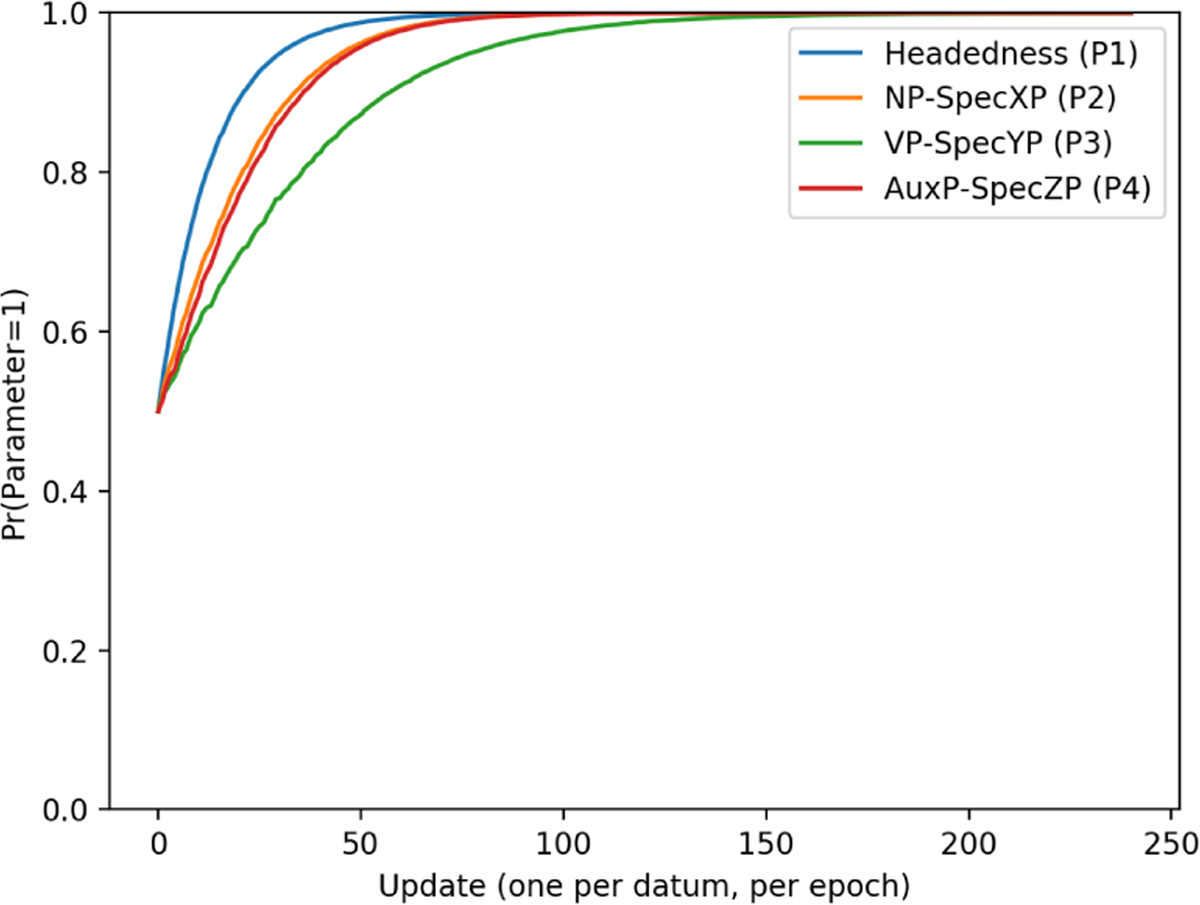
Unlike in the 3-token task, training data seen by the learner in the 2-token task was comprised of languages which only contained variants of {Auxiliary, Noun} and {Verb, Noun}. This means that the learner never saw any strings that actually violated the FOFC, only combinations of binary orders that would or would not predict such a violation. Learning curves for each individual word order pattern can be seen in Figure 10.
These results diverge minimally from the results seen in Figure 1 (where there were three datums per language), with respect to the relative ease at which the learner acquired settings for each language pattern. The difference between the learnability of each pattern can again be illustrated by looking at how long it takes the learner to 80% accuracy. The pattern with the steepest curve is the harmonic head-final word order, where the EDPL reaches 80% accuracy by about 12 passes through the data. This is followed by the harmonic head-initial and initial-over final orders, which take 25 and 30 passes through the data respectively for the learner to reach 80% accuracy. The pattern with the flattest curve (and therefore the most difficult) was the final-over-initial pattern, which in this case predicts (but does not explicitly include) structures that violate the FOFC. The learner does not achieve 80% accuracy on the final-over-initial pattern until about 47 passes through the data, requiring more than three times the amount of data than was needed for the head-final pattern.
Exposing the learner to fewer tokens had the effect of slowing down learning. While the learner took around 50 epochs to converge (or nearly converge) on all patterns in the 3-token task (1), learning took around 80 epochs in the 2-token task (10). This is unsurprising. The absence of the ternary tokens introduced more ambiguity, since they disambiguated some of the languages in the 3-token task, and this took the learner longer to resolve.
There are two additional (and more interesting) differences between results for the 3-token and 2-token tasks. The first is that, as previously noted, the head-initial harmonic pattern and the initial-over-final pattern had overlapping curves in the 2-token task, but not the 3-token task. The reason for this is that the head-initial harmonic pattern was slightly more difficult in the 2-token task. This can be seen by looking at the parameter curves for this language in Figure 11.
The learner fails to completely converge on parameter settings for this pattern by 160 updates (by which time parameters for other patterns had all converged). This actually takes about 700 updates to be completed. There is also a significant difference in the path of the parameter curves in the 2-token task. Here, P2 initially drifts towards 1 before changing course at about 30 updates. P3 also plateaus initially before drifting towards 1, creating the pincer configuration in Figure 11 that is absent in Figure 4. The reason for this can be seen by looking at the preference of just the binary tokens for 1 in Table 11.
Preference of head-initial tokens for 1.
| Inputs | Headedness (P1) | NP→XP (P2) | VP→YP (P3) | AuxP→ZP (P4) |
| V-O | 0.17 | 0.33 | 0.67 | 0.33 |
| Aux-O | 0.13 | 0.5 | 0.5 | 0.63 |
For P3, one token favors 1 and the other is at chance, while P4 is pushed in different directions by each token. This accounts for the initial drifting of P3 towards 1 and the initial plateauing of P4. Both P3 and P4 change course around the point where P1 is set to 0. The reason they change course can be seen by looking at the approximate weight of each parameter at 40 updates. This is given in Table 12.
Probability of P=1 at 40 updates.
| P1 | P2 | P3 | P4 |
| 1 | 0.8 | 0.45 | 0.45 |
Given these probabilities, the approximate weight of the languages that remain after P1 reaches 0 is as in Table 13.
Weight of each head-initial language at 40 updates.
| 0011 | 0001 | 0000 | 0010 | 0111 | 0101 | 0100 | 0110 |
| 0.242 | 0.198 | 0.162 | 0.198 | 0.060 | 0.049 | 0.040 | 0.049 |
At this point the combined weight of the remaining languages where P4=1 is 0.551, so it is greater than the combined weight of languages where P4=0 (0.449). This is why P4 begins to drift towards 1. The only head-initial language where P3 and P4 have different settings is 0101, and so after P4 starts moving towards 1, these two parameters ‘push against’ each other, causing P3 to drift towards zero. After P2 is set to zero, only one more parameter needs to be set, as discussed in section 5.2. P4 converges first, and so P3 plateaus.
The about-face that the P3 & P4 curves do in Figure 11 cause learning to be slightly more difficult when the learner is only exposed to 2-tokens. This additional difficulty is what allows the initial-over-final pattern to overtake the head-initial pattern in Figure 10, where this did not occur in Figure 1.
The second difference between the two tasks is that the learner consistently picked one parameter setting for the final-over-initial pattern in the 2-token, but not the 3-token task. All other parameter settings that the learner found for each word order pattern in the 2-token task were the same ones it found in the 3-token task, as seen in Table 14.
Parameter settings learned for word order patterns in each task.
| 3-token task | 2-token task | |
| a. Head-final | 1~0~ | 1~0~ |
| b. Head-initial | 00~1 | 00~1 |
| c. Initial-over-final | 01~1 | 01~1 |
| d. Final-over-initial | 1110 (40 %)/0010 (60%) | 0010 |
That the learner consistently arrived at a setting of 0010 for the final-over-initial order in the 2-token task can been seen by looking at the parameter curves for this pattern, given in Figure 12.
Parameter curves for the head-final and initial-over-final orders, which did not diverge significantly from the 3-token task, can be seen in the appendix. In Figure 12, we can see that P1 and P2 are consistently set to 0, where in the 3-token task, they were only set to 0 approximately 40% of the time. The reason this difference arises can be determined by looking at the preference that each binary final-over-initial token has for 1 in Table 15.
Preference of final-over-initial tokens for 1 (2-token).
| Inputs | Headedness (P1) | NP→XP (P2) | VP→YP (P3) | AuxP→ZP (P4) |
| V-O | 0.17 | 0.33 | 0.67 | 0.33 |
| O-Aux | 0.87 | 0.5 | 0.5 | 0.37 |
The general pattern here is much the same as in the 3-token task. P3 is still pushed towards 1, since one token is correlated with a setting of 1 on that parameter, and the other is at chance. P4 is likewise still pushed towards 0, since both binary tokens are correlated with this setting. In addition, P1 is still pulled in different directions by each datum, and P2 is pushed towards 0 by V-O, while O-Aux is not informative. What makes the learner able to consistently decide on parameter settings across runs in the 2-token experiment (where it was not able to when faced with three tokens) is the fact that the correlation of V-O with 0 has more weight in the 2-token experiment. That is to say, in the 2-token condition, half the tokens push the learner to 0 on P2, while only a third do when there are three datums. So in the 3-token condition, on a minority of runs the learner ends up finding the 1110 language, while in the 2-token condition, the impact of V-O pushes the learner towards setting P2 to 0. Since the data pushes the learner in different directions for P1, and since P1 and P2 must have the same setting for learning to be successful, this additional push towards 0 on P2 is sufficiently strong that the learner consistently lands on the 0010 language for this pattern.
The final-over-initial pattern still has the flattest curve in Figure 10, where all word order patterns are compared on the 2-token data. The reasons for this are the same reasons this pattern proved to be the most difficult when the learner was faced with three tokens. Firstly, all four parameters must be set for learning to be successful, where every other pattern required a maximum of three. Secondly, the learner is pulled in different directions on the first parameter, which must crucially have the same setting as the second. Even though it takes the learner less time to arrive at a solution for the final-over-initial pattern than it did for the harmonic head-initial and initial-over final patterns, this is because mistakes are frequent before the correct settings are achieved in the final-over-initial pattern, where as the slow patterns were slow by virtue of the fact that they made very few mistakes.
7 Discussion & Conclusion
The learning tasks conducted here used a domain-general statistical learner for parameter systems (EDPL). There is nothing about this learner that ensured it would struggle to learn final-over-initial word order patterns, or easily learn head-final languages. Additionally, there was nothing built into the syntax which generated the training data that made final-over-initial languages inherently more difficult. They were fully derivable, and there were no built-in penalties that would make them more costly to derive.
Instead, the relative difficulty posed by each word order pattern arose from the interaction of the learner with the data. The extent to which a word order pattern was challenging was a product of how easy it was for the EDPL to locate a parameter setting in the hypothesis space that would result in a high degree of accuracy. The head-final harmonic pattern was the easiest (in both tasks) because only two parameters needed to be set and, in the case of the 3-token task, one of them was disambiguated by the ternary token. This is contra the prediction of Kayne (1994), which takes head-initial structures to be more basic and predicts that they will therefore be the most common. It is supported, however, by cross-linguistics data from WALS, which lists more SOV languages than SVO (Dryer 2013).11 In the 3-token task, the second easiest was the harmonic head-initial pattern, where three parameters needed to be set, and two were disambiguated by the ternary token. In the 2-token task, no head-initial parameters were disambiguated, which resulted in some additional difficulty added by a change in direction of the weighting of two parameters. The initial-over-final pattern was comparable to the head-initial in the 2-token task, and third-easiest in the 3-token because three parameters needed to be set, and none of them were disambiguated by any token. The hardest pattern to learn in both tasks was the final-over-initial, which was the only pattern to contain *FOFC strings.
The reason that the EDPL struggled with the final-over-initial word order was twofold: first, all four parameters needed to be correctly set for the learner to achieve accuracy. There was never a point where any individual parameter settings ceased to matter. This was not the case with the harmonic orders, or the initial-over-final disharmonic order, where at most three parameters needed to be set before the learner reached 100% accuracy. The second reason that the EDPL struggled with the final-over-initial pattern is that the two possible parameter settings for this order pulled the learner in different directions. These parameter settings were 1110 and 0010, and since they have opposite settings on the first two parameters, responsibility for matches was attributed to both 1 and 0. P1 and P2 were also interdependent, and needed to have the same setting in order for the target language to be acquired. The result of this was that the parameter space for final-over-initial languages was not as contiguous as it was for the other word order patterns (i.e. 0010 and 1110 were not contiguous in the hypothesis space), and this created a greater challenge for the learner. In the 3-token task, the learner was unable to consistently pick parameter settings for the final-over-initial pattern. On about 60% of runs, it learned 0010, and 1110 on the additional 40%, and crucially, it did so with the flattest over-all curve. In the 2-token task, the learner did consistently learn 0010, but the learning still happened at a much flatter curve than with any other pattern.
7.1 Relating results to the model
The syntactic system that generated the training data starts with an spine of form {ZP Z, {YP Y, {AuxP Aux, {XP X, {VP V, {NP N}}}}}. This unlinearized input is taken to be a part of UG in this model.12 As stated in section 2, the null heads X, Y, Z, along with the assumptions of anti-locality, were adopted to optimize for a small parameter space, in order to make the results more transparent. It is plausible that, with additional parameters, null heads and anti-locality could be done away with without significantly impacting the results. Further speculation on what the mechanics of such a parameter system might look like are outside of the scope of this paper, but it would presumably need to produce an identical or highly similar typology.
The approach to linearization and the absence of rightward movement are less innocent, and have a significant effect on the results. First let us consider the impact of movement: One important factor contributing to the difficulty of the final-over-initial order was the fact that there were only two possible languages (parameter settings) compatible with this data, and they were sufficiently different from each other that the EDPL struggled to decide on the correct settings for each parameter. The learner got caught between two dissimilar, but equally good choices. Had there been additional languages, this would have smoothed out the parameter space by changing the correlation between final-over-initial tokens and parameter settings. For example, if the final-over-initial pattern had been generated by 1110, 0010, and 1010, then it would have been easy for the learner to set P1 to 1, since 2/3 languages would have this setting. Likewise P2 could have easily been set to 0, for the same reason. However, since there were only two languages, 1110 and 0010, there was no ‘tie-breaker’ to guide the learner to one setting over the other. The reason that this didn’t happen in the case of the initial-over-final order (i.e. the other disharmonic pattern), is that there are more weakly-equivalent initial-over-final languages. The presence of more contiguous, weakly-equivalent languages allowed the learner to determine that some settings were more likely to produce matches than others, so that no parameter ended up ‘tied’ between 1 and 0.
This asymmetry between final-over-initial and initial-over-final languages is reducible to the asymmetry between leftward and rightward movement. Although both disharmonic patterns have two minimal derivations (section 3), further string-vacuous leftward movements create a number of additional weakly-equivalent initial-over-final languages. Leftward movement does not create additional weakly-equivalent languages for the final-over-initial pattern, as no leftward movement applied after those in the minimal derivations is string vacuous. Any additional movement applied to a final-over-initial structure results in a different word order. In order to introduce vacuous movement that could produce more weakly-equivalent final-over-initial languages, rightward movement would need to be introduced to the system.
This brings us to headedness, and the question of whether the asymmetry between leftward and rightward movement is sufficient to reproduce the attested typology under any system of linearization. I will not attempt to provide a fully comprehensive answer to this question here, but will instead focus on showing how assuming base-generation of harmonic extended projections contributes to the results. The first contribution is in fact a part of the justification for adopting this version of a linearizing parameter; defining headedness over extended projections effectively captures the fact that the FOFC does not appear to hold across them. For example, if determiners are added to the data set, along with a parameter for determining the order of D and NP, this will not affect the difficulty of any class of languages. The additional parameter needed to control the headedness of DP would double the size of the hypothesis space, but it would do so evenly across all patterns, so the relationship between data points and parameter settings would be unchanged.
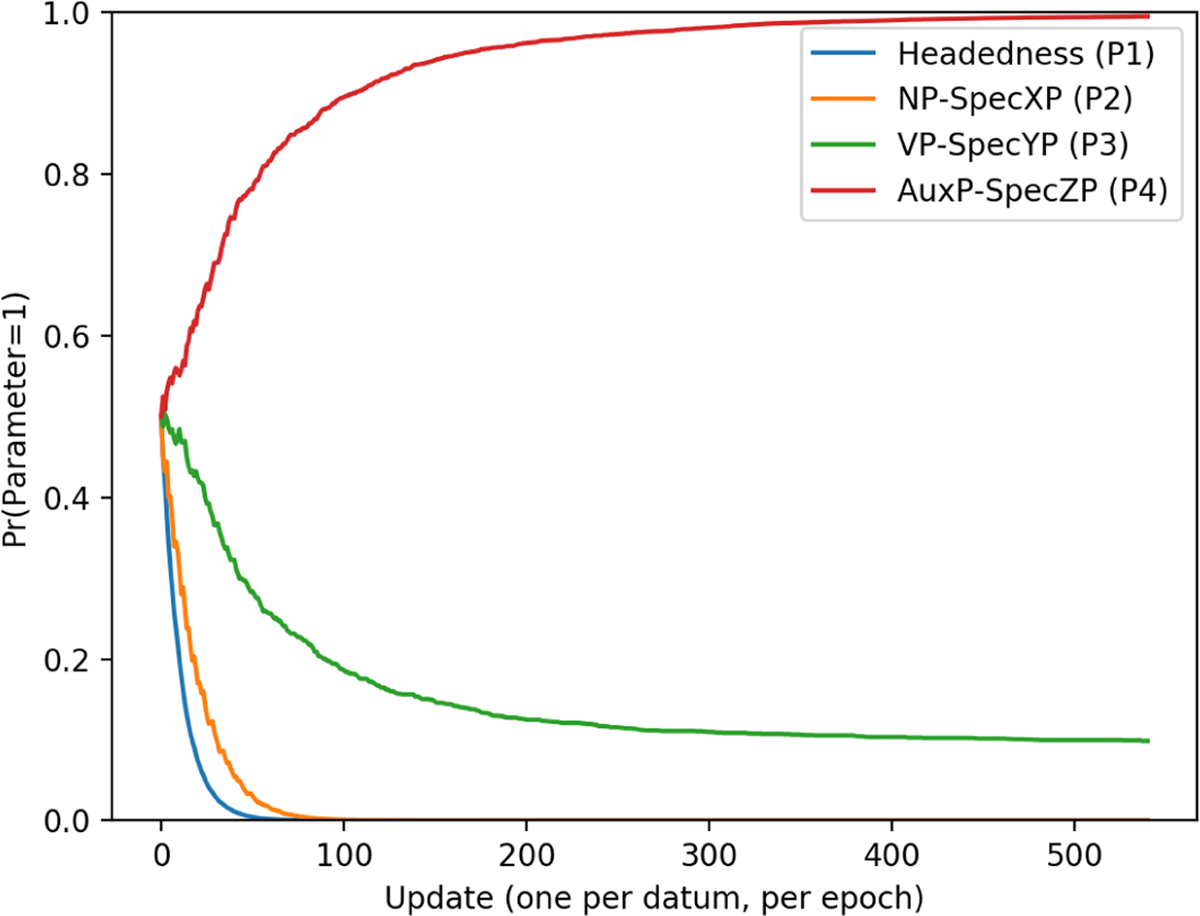
Outside of explaining why the FOFC does not cross extended projections, defining headedness as underlyingly harmonic also introduces an important asymmetry between the harmonic and disharmonic languages. The ability to be base-generated increases the number of harmonic languages in a way that is contiguous, and therefore makes them easier to learn. If headedness was decided for each XP individually, as proposed in Abels & Neeleman (2012), this asymmetry would be lost, and the number of disharmonic languages would be greatly increased. Without this difference between harmonic and disharmonic languages, the remaining asymmetry between leftward and rightward movement is insufficiently strong for capturing the typological distribution of word order patterns. This is shown in Figure 13, which gives the parameter curves for a simulation identical to the 3-token task, with the exception that there were two separate parameters determining the headedness of AuxP and VP.
As this figure shows, when any order can be base-generated, the resulting curves bear no resemblance to the word order typology described in the literature. Therefore the asymmetry between the harmonic and disharmonic languages conspires with the absence of rightward movement to produce the hypothesis space that will lead the learner to mimic the frequency of word order patterns in natural language typology. The EDPL in particular does this because it is sensitive to the smoothness of the parameter space, which is why it struggles more when the languages within a word order pattern have discontiguous settings, as in the case of the final-over-initial pattern. More specifically, the EDPL is sensitive to the contribution of individual parameter settings to a match or mismatch. This is what leads it to get stuck between 1110 and 0010 for the final-over initial languages, as discussed above. Learners that are similarly sensitive to smoothness could conceivably be used to achieve comparable results.
7.2 Richness of the data
What I have done in this paper is to show that typologically marked orders like V-O-Aux, which violate the FOFC, may have a starting bias linked to how difficult it is for a learner to locate an appropriate grammar for them in the hypothesis space of languages. To have a more definitive answer about whether the FOFC stems from learning, the next step for this project is to model how this bias might be translated across generations. Although beyond the scope of the work presented here, iterated learning will stress-test the results by showing whether the bias is amplified as predicted, and also what word order(s) is(are) predicted to be learned in place of FOFC violators.
Additionally, the data used in this model is necessarily a vast oversimplification of the challenge that actual language learners are presented with, as is the standard in computational modelling work of this kind. Because of this, it is natural to wonder whether the results would be preserved with a richer data set that more accurately reflected the kind of input human learners receive. It is currently impractical if not impossible to model acquisition of the full extent of natural language data a human child is exposed to, of course, but a reviewer raises the question of a few areas relevant to the FOFC that one could imagine might affect the results. First is the question of how the learner might handle scrambling languages, which have variable word order but still seem sensitive to the FOFC. While there is no way to definitively answer this question without testing it, but depending on how scrambling is implemented, it is very possible that the results will be reserved (for instance, one might expect a similar hypothesis space to emerge if scrambling is implemented by making movement operations either fixed or optional). This is a natural next step for the project, although it is beyond the scope of the present work. There is also the (twofold) question of adverbs, which a) exhibit FOFC-like effects in V-Adv-Aux sequences, and b) seem to disambiguate movement where it might be string vacuous in other cases. In the first case, since the model learns sequences of stings without really “knowing” what a word is, a minimally different typology with V-Adv-Aux tokens would produce the same results. It may be necessary to make different syntactic assumptions about the hierarchical configurations that generates V-Adv-Aux sequences, but since the learner never has access to this information anyways, it would be not be expected to effect the results of the model unless the assumptions generated a wildly different distribution of word orders. This is likewise true of any other FOFC-like configuration (the head-final filter, etc). In terms of adverbs ability to provide cues for learning word orders, adverbs position varies greatly across and even within languages and this brings into question the amount of information they can really provide to a learner trying to acquire word order. It is not clear to me that they are predictable enough to be disambiguating. That being said, the question of how the model presented here behaves with a richer data set is an interesting one that should be investigated in future, especially in light of research in the Iterated Learning Framework (Kirby 1999; Smith et al. 2003; Kirby et al. 2004) that shows how weak biases (like the one put forward here) may be amplified into strong generalizations when transmitted across generations.
7.3 Broader connections
It is important to note that the source of the problem with final-over-initial pattern is the difficulty that the learner has trying to decide on a parameter setting for these languages. This means that it is not actually the *FOFC string which is challenging for the learner, but rather locating parameter settings that will produce that string in the hypothesis space. This is confirmed by the 2-token task, where the learner was never exposed to strings that violated the FOFC, but still struggled to acquire languages where such strings might be predicted to appear. The results of the 2-token task mirror the results of an adult learning study conducted in Culbertson et al. (2012). The purpose of their study was to investigate whether or not adult language learners are biased against learning typologically infrequent word order patterns in the nominal domain. Specifically, it dealt with Greenberg’s Universal 18, which observes that when adjectives precede a noun, numerals and demonstratives generally do as well (Greenberg 1963). This universal is sometimes considered to be a part of the FOFC, as the marked word order Adjective-Noun-Numeral can be modelled with a *FOFC structure. In the experiment, adult learners were exposed to miniature artificial languages that had an inconsistent mix of word order patterns (an idealization of change in progress), and then tested on what they had learned. Culbertson et al. found that when the artificial language had dominant harmonic and unmarked disharmonic orders, learners shifted that language towards the majority order (i.e. produced the majority order at a greater frequency than it was found in the training data). When the dominant order was the marked disharmonic pattern, learners shifted the language towards a harmonic order, instead of reinforcing the dominant order in the training data. Crucially, learners in this study only learned binary sequences of {Adjective, Noun} and {Number, Noun}. As in the 2-token learning task conducted here, the human learners in Culbertson et al. dispreferred learning the constructed languages which would predict a FOFC violation, without ever actually being exposed to a *FOFC structure.
Although the final-over-initial pattern was consistently the most difficult to learn, the EDPL never actually failed to converge on parameter settings for final-over-initial languages in either task. This result is compatible with the idea that the challenges *FOFC word orders pose to a learner may be a source of the rarity of those word orders. If the challenges presented by the final-over-initial pattern do not necessarily make it impossible for *FOFC orders to be learned, then this allows for the existence of exceptions to the FOFC, which have been documented in the literature (Bhatt & Dayal 2007; Biberauer et al. 2014; Erlewine 2017; Sheehan et al. 2017). Additionally, the relative order of the other word-order patterns likewise parallels the typology, with the exception of the ranking of head-initial and initial-over-final languages in the 2-token task. In both tasks, all languages were easier than the final-over-initial pattern, and in the 3-token task, harmonic languages were also easier to learn than disharmonic, even when the disharmonic language did not violate the FOFC.
A Appendix
A.1 Head-initial + VP fronting & Head-final + AuxP fronting
In the head-initial + VP fronting pattern, all parameters are set quickly, and this is because there is only one possible language. Since ternary tokens are unique to a language pattern, the ternary form disambiguates every parameter setting in patterns containing only one language. This can be seen in Table 16.
Preference of head-initial + VP fronting tokens for 1.
| Inputs | Headedness (P1) | NP→XP (P2) | VP→YP (P3) | AuxP→ZP (P4) |
| V-O | 0.17 | 0.33 | 0.67 | 0.33 |
| Aux-O | 0.13 | 0.5 | 0.5 | 0.63 |
| V-Aux-O | 0 | 1 | 1 | 0 |
This is likewise true for the head-final + AuxP fronting word order pattern, which consists of a single language comprised of the tokens O-Aux, O-V, and O-Aux-V. Parameter curves for this language are given in Figure 15.
The learner is able to set each parameter quickly because there is only one language in this pattern, and therefore the ternary token disambiguates each parameter setting, as seen in Table 17.
Preference of head-final+ AuxP fronting tokens for 1.
| Inputs | Headedness (P1) | NP→XP (P2) | VP→YP (P3) | AuxP→ZP (P4) |
| O-V | 0.7 | 0.6 | 0.4 | 0.6 |
| O-Aux | 0.87 | 0.5 | 0.5 | 0.37 |
| O-Aux-V | 1 | 1 | 1 | 1 |
Notes
- Steinert-Threlkeld & Szymanik (2019; 2020) show how learnability can be related to typology in the domain of semantics, although use of neural nets in that work makes the mechanisms by which these asymmetries arise less transparent than in other works cited here. [^]
- While models for syntactic parameter learning are given in Gibson & Wexler (1994); Fodor (1998); Yang (2002); Gould (2015; 2016); Sakas et al. (2018); Prickett et al. (2019), these works focus on modeling how parameter setting might be achieved given ambiguous evidence, rather than how the shape of the parameter space might influence typology. [^]
- Other analyses couched in OT do not necessarily prohibit exceptions to the FOFC, due to the nature of violable constraints, as in Kusmer (2020); DelBusso (2020). [^]
- The implementation of the EDPL used here is the same as in Prickett et al. (2019), written by Brandon Prickett, with minor modifications. [^]
- See Stanton (2016) for similar discussion of antagonistic learning pressures in phonology. [^]
- This should not be taken to suggest that the existence of such phrases outside the bounds of what is normally proposed in syntax. For example, potential identities for XP, YP, and ZP could be the commonly assumed vP, TP, and CP phrases. Many options are also provided by syntactic cartography (e.g. in Cinque (1999)). Since it is the structural relationship between heads that will have a role to play in the learning experiment, this paper does not detour into the minutiae of what labels are most appropriate. [^]
- A reviewer points out that Biberauer et al. (2014) employ a non-traditional notion of extended projection in order to capture the domain FOFC operates over. I follow them in calling this ‘extended projection,’ with the understanding that it may not be the exact domain originally proposed in Grimshaw (1991). [^]
- Additionally, movement always occurs from the bottom up, a universal assumption in generative syntax, so the ordering of movements is fixed. [^]
- Runs represent individual learners, while passes through the data (i.e. ‘epochs’) represents the number of times the learner saw each token. [^]
- To clarify; this has nothing to do with the fact that the remaining parameters would produce sting vacuous movement – the learner cannot distinguish vacuous from non-vacuous movement. The parameters are irrelevant because no matter their setting, the learner will always produce the right string. [^]
- Thank you to an anonymous reviewer for pointing this out. [^]
- Potentially this hidden structure could also be taken as something that is learned prior to the slice of learning examined here. How the underlying form would be learned prior to the word order is unclear, but one possibility is that it could be tied to the conceptual strength of association between worlds, along the lines of Culbertson et al. (2019) [^]
Acknowledgements
Versions of this work have been presented at NELS 51, UC Berkeley SSCircle, and at the UMass Amherst Syntax Workshop. I am grateful to these audience for their helpful discussion, and to Gaja Jarosz and Kyle Johnson for comments and feedback, and to Brandon Prickett for sharing with me his implementation of EDPL. Additionally, this paper has benefited greatly from the comments of three anonymous reviewers.
Competing interests
The author has no competing interests to declare.
References
Abels, Klaus. 2003. Successive cyclicity, anti-locality, and adposition stranding: University of Connecticut Storrs, CT dissertation.
Abels, Klaus & Neeleman, Ad. 2012. Linear asymmetries and the LCA. Syntax 15(1). 25–74. DOI: http://doi.org/10.1111/j.1467-9612.2011.00163.x
Baker, Mark C. 1996. The polysynthesis parameter. Oxford Studies in Comparative Syntax, Oxford University Press.
Baker, Mark C. 2008. The macroparameter in a microparametric world. In Biberauer, Theresa (ed.), The limits of syntactic variation, 351–374. Amsterdam: John Benjamins. DOI: http://doi.org/10.1075/la.132.16bak
Bhatt, Rajesh & Dayal, Veneeta. 2007. Rightward scrambling as rightward remnant movement. Linguistic Inquiry 38(2). 287–301. DOI: http://doi.org/10.1162/ling.2007.38.2.287
Biberauer, Theresa & Holmberg, Anders & Roberts, Ian. 2014. A syntactic universal and its consequences. Linguistic Inquiry 45(2). 169–225. DOI: http://doi.org/10.1162/LING_a_00153
Boersma, Paul. 2003. Review of Bruce Tesar & Paul Smolensky (2000). Phonology 20(3). 436–446. DOI: http://doi.org/10.1017/S0952675704230111
Breteler, J. 2018. A foot-based typology of tonal reassociation: Perspectives from synchrony and learnability. Utrecht, Netherlands: LOT.
Bush, Robert R. & Mosteller, Frederick. 1951. A mathematical model for simple learning. Psychological review 58(5). 313. DOI: http://doi.org/10.1037/h0054388
Cecchetto, Carlo. 2013. Backward dependencies must be short: A unified account of the Final-over-Final and the Right Roof Constraints and its consequences for the syntax/morphology interface 57. Berlin New York: Mouton de Gruyter. DOI: http://doi.org/10.1515/9781614512431.57
Cinque, Guglielmo. 1999. Adverbs and functional heads: A cross-linguistic perspective. Oxford University Press.
Clem, Emily. Forthcoming. Disharmony and the Final-Over-Final Condition in Amahuaca. Linguistic inquiry.
Culbertson, Jennifer. 2010. Learning biases, regularization, and the emergence of typological universals in syntax: Johns Hopkins University dissertation.
Culbertson, Jennifer & Schouwstra, Marieke & Kirby, Simon. 2019. From the world to word order: the link between conceptual structure and language. PsyArXiv. DOI: http://doi.org/10.31234/osf.io/v7be4
Culbertson, Jennifer & Smolensky, Paul & Legendre, Géraldine. 2012. Learning biases predict a word order universal. Cognition 122(3). 306–329. DOI: http://doi.org/10.1016/j.cognition.2011.10.017
DelBusso, Natalie. 2020. The Final-over-Final Condition, Stringency, and Typological structure. Linguistic Inquiry 51(4). 765–784. DOI: http://doi.org/10.1162/ling_a_00357
Dempster, Arthur P & Laird, Nan M & Rubin, Donald B. 1977. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society: Series B (Methodological) 39(1). 1–22. DOI: http://doi.org/10.1111/j.2517-6161.1977.tb01600.x
Dryer, Matthew S. 1992. The greenbergian word order correlations. Language (68). 81–138. DOI: http://doi.org/10.1353/lan.1992.0028
Dryer, Matthew S. 2013. Order of subject, object and verb. In Dryer, Matthew S. & Haspelmath, Martin (eds.), The world atlas of language structures online, Leipzig: Max Planck Institute for Evolutionary Anthropology. https://wals.info/chapter/81.
Erlewine, Michael Yoshitaka. 2017. Low sentence-final particles in Mandarin Chinese and the Final-over-Final Constraint. Journal of East Asian Linguistics 26(1). 37–75. DOI: http://doi.org/10.1007/s10831-016-9150-9
Fodor, Janet Dean. 1998. Parsing to learn. Journal of Psycholinguistic research 27(3). 339–374. DOI: http://doi.org/10.1023/A:1023255705029
Gibson, Edward & Wexler, Kenneth. 1994. Triggers. Linguistic inquiry 25(3). 407–454.
Goldwater, Sharon & Johnson, Mark & Spenader, Jennifer & Eriksson, Anders & Dahl, Östen. 2003. Learning ot constraint rankings using a maximum entropy model. In Proceedings of the workshop on variation within optimality theory. pp, vol. 111. 120.
Gould, Isaac. 2015. Syntactic learning from ambiguous evidence: Errors and end-states: Massachusetts Institute of Technology dissertation.
Gould, Isaac. 2016. Learning parameter setting from ambiguous evidence: Parameter interaction and the case of Korean. In Proceedings of the 33rd West Coast Conference on Formal Linguistics. somerville, ma: Cascadilla proceedings project, 157–166.
Greenberg, Joseph Harold. 1963. Some universals of grammar with particular reference to the order of meaningful elements. In Greenberg, Joseph Harold (ed.), Universals of language. Cambridge, MA: MIT press.
Grimshaw, Jane. 1991. Extended projection. Ms., Brandeis University.
Grohmann, Kleanthes K. 2003. Successive cyclicity under (anti-) local considerations. Syntax 6(3). 260–312. DOI: http://doi.org/10.1111/j.1467-9612.2003.00063.x
Grohmann, Kleanthes K. 2011. Anti-locality: Too-close relations in grammar. In Boeckx, Cedric (ed.), The oxford handbook of linguistic minimalism, 260–290. Oxford University Press: Oxford.
Hawkins, John A. 1983. Word order universals. New York: Academic Press.
Heinz, Jeffrey. 2010. Learning long-distance phonotactics. Linguistic Inquiry 41(4). 623–661. DOI: http://doi.org/10.1162/LING_a_00015
Holmberg, Anders. 2000. Deriving OV order in Finnish. In Svenonius, Peter (ed.), The derivation of vo and ov, 123–152. Amsterdam: John Benjamins. DOI: http://doi.org/10.1075/la.31.06hol
Hughto, Coral. 2018. Investigating the consequences of iterated learning in phonological typology. Proceedings of the Society for Computation in Linguistics 1(1). 182–185.
Hughto, Coral & Pater, Joe & Staubs, Robert. 2015. Grammatical agent-based modeling of typology. In Glow workshop on computation, learnability and phonological theory.
Jarosz, Gaja. 2015. Expectation driven learning of phonology. Ms., University of Massachusetts Amherst.
Jarosz, Gaja. 2019. Computational modeling of phonological learning. Annual Review of Linguistics (5). 67–90. DOI: http://doi.org/10.1146/annurev-linguistics-011718-011832
Kayne, Richard S. 1994. The antisymmetry of syntax. Cambridge, Massachusetts: MIT Press.
Kirby, Simon. 1999. Function, selection, and innateness: The emergence of language universals. OUP Oxford.
Kirby, Simon & Smith, Kenny & Brighton, Henry. 2004. From UG to universals: Linguistic adaptation through iterated learning. Studies in Language 28(3). 587–607. DOI: http://doi.org/10.1075/sl.28.3.09kir
Kusmer, Leland. 2020. Optimal linearization: Word-order typology with violable constraints. Syntax, 313–346. DOI: http://doi.org/10.1111/synt.12197
Mahajan, Anoop Kumar. 1990. The a/a-bar distinction and movement theory: Massachusetts Institute of Technology dissertation.
Müller, Gereon. 1997. Extraposition as remnant movement. Linguistik Aktuel l 17. 215–246. DOI: http://doi.org/10.1075/la.17.10mul
Müller, Gereon. 2002. Two types of remnant movement. In Alexiadou, Artemis & Anagnostopoulou, Elena & Sjef, Barbiers & Gärtner, Hans-Martin (eds.), Dimensions of movement: From features to remnants, 209–241. John Benjamins Amsterdam. DOI: http://doi.org/10.1075/la.48.10mul
Nazarov, Aleksei & Jarosz, Gaja. 2017. Learning parametric stress without domain-specific mechanisms. In Proceedings of the 2016 Annual Meeting on Phonology, vol. 4. DOI: http://doi.org/10.3765/amp.v4i0.4010
Nazarov, Aleksei & Jarosz, Gaja. in press. Domain general learning of parametric stress. Glossa.
Pater, Joe. 2012. Emergent systemic simplicity (and complexity). McGill Working Papers in Linguistics 22(1).
Potsdam, Eric & Edmiston, Daniel. 2016. Extraposition in Malagasy. In 22nd meeting of the Austronesian Formal Linguistics Association (AFLA), 121–138.
Prickett, Brandon et al. 2019. Learning syntactic parameters without triggers by assigning credit and blame. In Proceedings of the 55th Chicago Linguistics Society (CLS 55).
Roberts, Ian. 2017. Harmony, symmetry, and dominance in word order universals. In Sheehan, Michelle & Biberauer, Theresa & Roberts, Ian (eds.), The Final-Over-Final Condition: A syntactic universal, 27–42.
Roberts, Ian G. 2010. Agreement and head movement: Clitics, incorporation, and defective goals. Cambridge, MA: MIT Press. DOI: http://doi.org/10.7551/mitpress/9780262014304.001.0001
Ross, John Robert. 1967. Constraints on variables in syntax: Massachusetts Institute of Technology dissertation.
Sakas, William Gregory & Yang, Charles & Berwick, Robert. 2018. Parameter setting is feasible. Linguistic Aanalysis.
Sheehan, Michelle. 2011. Extraposition and antisymmetry. Linguistic variation yearbook 10(1). 201–251. DOI: http://doi.org/10.1075/livy.10.06she
Sheehan, Michelle. 2013. Explaining the Final-over-Final Constraint: Formal and functional approaches. In Biberauer, Theresa & Sheehan, Michelle (eds.), Theoretical approaches to disharmonic word orders, 407–44. Oxford: Oxford University Press. DOI: http://doi.org/10.1093/acprof:oso/9780199684359.003.0015
Sheehan, Michelle & Biberauer, Theresa & Roberts, Ian & Holmberg, Anders. 2017. The Final-over-Final Condition: A syntactic universal. Cambridge, MA: MIT Press. DOI: http://doi.org/10.7551/mitpress/8687.001.0001
Smith, Kenny & Kirby, Simon & Brighton, Henry. 2003. Iterated learning: A framework for the emergence of language. Artificial life 9(4). 371–386. DOI: http://doi.org/10.1162/106454603322694825
Stanton, Juliet. 2016. Learnability shapes typology: the case of the midpoint pathology. Language 92(4). 753–791. DOI: http://doi.org/10.1353/lan.2016.0071
Staubs, Robert D. 2014. Computational modeling of learning biases in stress typology: University of Massachusetts Amherst dissertation.
Steinert-Threlkeld, Shane & Szymanik, Jakub. 2019. Learnability and semantic universals. Semantics and Pragmatics 12. 4. DOI: http://doi.org/10.3765/sp.12.4
Steinert-Threlkeld, Shane & Szymanik, Jakub. 2020. Ease of learning explains semantic universals. Cognition 195. 104076. DOI: http://doi.org/10.1016/j.cognition.2019.104076
Yang, Charles. 2002. Knowledge and learning in natural language. Oxford University Press.
Zeijlstra, Hedde. 2016. Explaining FOFC without the LCA. In Presentation at the 47th Annual Meeting of the North East linguistic society.