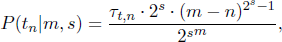1 Introduction
Agreement markers that index the same argument (e.g., person-number markers that express the subject of a transitive sentence) tend to occur in the same position within the word. For example, in the Baure (Arawakan) verbal paradigm in Table 1, all person-number agreement markers are prefixes. Mansfield et al. (2020) identified this tendency as a cross-linguistic bias towards category clustering. Here we explore the cases that run against this trend. One such case is illustrated by Fula (Atlantic-Congo), where person-number subject agreement markers are prefixes in some cases and suffixes in others. Our study focuses on agreement paradigms like this one in which markers of the same morphosyntactic role occur in different positions. When different values behave in different ways regarding the position they are marked in, this gives rise to a split (Corbett 2015) at the paradigmatic level. We will refer to these cases as positional splits.
Subject agreement markers (in bold) in Baure (Arawakan) (Danielsen 2007: 31) and Fula (Atlantic-Congo) (Arnott 1970: 191–192). Same-shade indicates values marked in the same position. Different shades correspond, thus, to differences in the position of markers, i.e., to positional splits.
| Baure ‘arrive’ PST | Fula ‘wash’ REL.PST.PASS | |||
| sg | pl | sg | pl | |
| 1 | ni-šim | vi-šim | lootaa-mi | min-lootaa |
| 2 | pi-šim | yi-šim | loota-ɗaa | lootaa-ɗon |
| 3 | ro-šim | no-šim | ‘o-lootaa | ɓe-lootaa |
Variability in affix ordering and discontinuity in affix marking (i.e., agreement that is realised in two different positions within the same word) have attracted a lot of attention in linguistic theory and typology (e.g., Shlonsky 1989; Noyer 1992; Stump 1997; Hyman 2003; Crysmann & Bonami 2016; Harris 2017). They represent descriptive and analytical challenges in the languages and families where these phenomena are common (Inkelas 1993; Bickel et al. 2007; Caballero 2010). It is hard, in many of these cases, to determine what is the mapping between form and meaning, or the inflectional rules morphemes follow. Many efforts have been devoted to arguing whether specific cases are best described with reference to morphosyntactic/semantic (Muysken 1986; Rice 2000) or phonological principles (Rice 2011), or whether they follow morphological templates which are blind to the morphosyntax and semantics of morphemes (Stump 1997; Good 2016).
Here we examine positional splits in terms of the features and values that characterise them. We focus purely on the positional arrangements of cumulative1 person-number markers (i.e. their position relative to the stem as well as other markers), and gloss over the morphology of the markers, including the presence of the same marker across multiple paradigmatic cells. For example, in Fula (Table 1), we find a split between 1sg=2sg=2pl (suffixal) and 3sg=1pl=3pl (prefixal) markers. Examining splits in this way is motivated by research on syncretism, where the sharing of feature values across cells in a paradigm (often referred to as natural classes) has informed abstract morphological-architectural principles (Blevins 1995; Harley & Ritter 2002; Baerman et al. 2005; Pertsova 2007; Harbour 2016; Bobaljik & Sauerland 2018), as well as by debates surrounding the ‘morphome’ (i.e., a term given to a set of semantically disparate values characterised by the same morphological form; Aronoff 1994; Luís & Bermúdez-Otero 2016; Maiden 2018; Herce 2023). Saldana et al. (2022), for example, showed that unnatural syncretic patterns (patterns without a shared feature value across all cells) with more feature value overlap (i.e., higher semantic similarity) are more frequent cross-linguistically and easier to learn in an artificial language learning experiment. These results suggest that the degree of semantic similarity within patterns of syncretism impacts the learnability of more or less unnatural patterns of syncretism and ultimately their cross-linguistic recurrence: The higher the semantic similarity within a pattern, the easier it is to learn. The authors suggest that this gradient in learnability may reflect a general bias towards similarity-based structure in morphological paradigms (see also, e.g., Pertsova 2014; Nevins et al. 2015; Nevins 2015; Maldonado & Culbertson 2022), which previous literature has shown to play a crucial role in phonology (Moreton & Pater 2012; Pater & Moreton 2012; Moreton et al. 2017: e.g.,) and word learning (Landau & Shipley 2001; Pothos et al. 2004; Xu & Tenenbaum 2007; Dautriche et al. 2016; Silvey et al. 2019; Carr et al. 2020) as well as in category and concept learning more generally (Bruner et al. 1956; Shepard et al. 1961; Neisser & Weene 1962; Gottwald 1971; Goodman et al. 2008). Together, these studies suggest a characterisation of naturalness as a matter of degree, computed as the average feature value overlap across cells in a pattern. Here we examine the applicability of this notion with regards to the position, rather than the form, of markers.
While positional variability and paradigmatic splits have both received substantial attention separately, there is, apart from occasional observations (Bickel 1994; Cysouw 2003: 310; Trommer 2003; Campbell 2012), no substantial research bringing these phenomena together. It remains largely unresolved whether positional patterns follow similar principles as those governing patterns of syncretism or whether principles differ between these types of paradigmatic splits. In this study we explore positional splits in two ways: 1) First we assess their cross-linguistic distribution, and since (non-absolute, statistical) trends in these distributions are the product of transmission over time (e.g., Greenberg 1966; Kirby et al. 2004; Bickel 2007; Culbertson et al. 2012; Bickel 2015), 2) we ask whether trends might be driven by cognitive biases favouring the learning and transmission of specific patterns. To explore these questions we combine quantitative typology with experimental methods.
The structure of the paper is as follows: Section 2 surveys positional splits and explains how we operationalise them in this study. Section 3 analyses the cross-linguistic data, asking which splits are over- or under-represented. Section 4 reports two artificial language learning experiments that we conducted to probe the learnability (by adults) of different split types. Section 5 contains a discussion of the cross-linguistic and experimental data and their significance. The concluding Section 6 summarises the paper’s findings and claims.
2 Typology of positional splits
Many factors can influence the positional properties of affixes. The most obvious one is the feature (e.g., person, number, tense, polarity, etc.) that an affix marks. Since regularity and predictability are generally preferred in language (see, e.g., Ackerman & Malouf 2013; Saldana et al. 2019; Mansfield et al. 2020; Saldana et al. 2021b; Mansfield et al. 2022), we expect subject agreement markers to appear in the same position as other subject agreement markers. This positional consistency of markers should hold across the two different aspects, comprised within the principle of category clustering (Mansfield et al. 2020):
I) Across the different concrete values that the affixes themselves express: i.e., if a subject affix expresses cumulatively number and person agreement, any combination of person (1,2,3) and number (sg and pl) values is expected to be marked in the same position because they all provide information about the same argument. By ‘position’ we refer to the same linear order relative to both the root and any other morphs, also known as ‘slot’ in templatic approaches (McCarthy 1981; McCarthy & Prince 1990). Crysmann & Bonami (2016: 317) call this Paradigmatic Alignment.
II) Across any other orthogonal values: i.e., the person.umber subject agreement marker would be expected to appear in the same position in past and present tenses, across different verbs (e.g., in the verb ‘kill’ and in the verb ‘split’), in declarative and interrogative sentences, positive and negative polarity, active and passive voice, etc. Stump (2001: 20) calls this Featural Coherence.
The focus of this paper is on deviations from principle I), and more specifically on subject and object agreement markers whose position with respect to other markers or the stem varies as a function of the specific person and number values they encode. The reason for this focus is twofold: i) subject/object agreement is exceptionally widespread cross-linguistically (and there is therefore more data available than for most other inflectional features), and ii) its component features (person and number) and values (e.g., 1, 2, 3, and sg, pl) are much easier to detect and separate than other semantic domains in morphology. While tense, aspect, and mood values, for example, are usually difficult to identify with certainty, and are often impossible to arrange in a tabular structure of compatible vs incompatible values, person and number are less subject to such problems. We follow the traditional typological nomenclature and refer to markers of transitive subjects as A markers (which stands for agent, because it is most likely to be one), to intransitive subject markers as S markers (which stands for sole argument), and to object markers as P (which stands for patient, because it is most likely to be one).2
In this paper we will ignore inclusive (i.e., 1+2(+3)) forms so as to have fully orthogonal and mutually compatible feature values. Moreover, due to greater data availability, we will focus exclusively on 3×2 (person:1, 2, 3; number:sg,pl) paradigms exclusively, ignoring dual (or trial/paucal) in the very few languages where these are different from plural in our sample.3
Although the number and type of morphosyntactic features and values assumed in person-number paradigms varies to some extent across theories (e.g., Harbour 2016), the existence of separate features of person based on the roles of participants in the speech act and number based on cardinality is comparatively uncontroversial (Cysouw 2003). In our analysis we assume a person feature with the three possible values speaker (or 1), addressee (or 2), and other (or 3), and a number feature containing the values singular and plural. Under this ternary feature analysis of person, we then assume that speaker is defined4 iff the entity denoted contains the speaker (and excludes the addressee in systems with clusivity and thus 1pl.inclusive forms, which we exclude), and addressee is defined iff the entity denoted contains the addressee and excludes the speaker (Schlenker 2003; Heim 2008); other is then specified only in competition with speaker and addressee and thus iff the entity denoted does not contain neither the speaker nor the addressee. singular is defined iff the cardinality of the entity denoted is equal to 1, and plural iff the cardinality of the entity denoted is greater than 1. Table 2 summarises our assumed person-number feature structure.
Decomposition of the assumed person-number feature structure.
| person | number | |
| 1SG | speaker | singular |
| 2SG | addressee | singular |
| 3SG | other | singular |
| 1PL | speaker | plural |
| 2PL | addressee | plural |
| 3PL | other | plural |
A word of clarification is also needed regarding the possible splits in A/P/S agreement markers. Along with the features and values that concern us here (i.e., the person and number values that the morphs themselves encode), any other orthogonal features and values may be associated with a different order of the agreement markers. Differences in the positioning of these affixes sometimes depend on factors independent of person-number, such as tense-aspect-mood (TAM hereafter) (like in Amele, see Table 3; Roberts & Roberts 1987), lexical class, (like in Somali, Saeed 1999), polarity (like in Mari, Ackerman & Malouf 2016), or voice. For example, in Table 3 we observe that in certain TAM values of Amele (e.g., in the habitual past), person-number affixes follow the TAM marker (-lo), while in other TAMs (e.g., today’s past) they precede the TAM marker (-a). This is a positional split that violates featural coherence, but not paradigmatic alignment. When factors other than the person-number values of the affixes are held constant, no positional differences are found (i.e., -ig, -i, -u, -si, etc. are all found in the same position). These cases do not count, therefore, as instances of paradigmatic positional splits as defined for our purposes.
Partial person-number subject verbal agreement paradigms in Amele (Trans-New Guinea) for the verb ho ‘come’ (Roberts & Roberts 1987). These illustrate a tense-based positional split: Person-number markers (in bold) in habitual past appear following the TAM marker and in today’s past they follow the stem and precede the TAM marker.
| Habitual past | Today’s past | |||
| sg | pl | sg | pl | |
| 1 | ho-l-ig | ho-lo-b | hu-g-a | ho-q-a |
| 2 | ho-lo-g | ho-lo-ig | ho-g-a | ho-ig-a |
| 3 | ho-lo-i | ho-lo-ig | ho-i-a | ho-ig-a |
In the most complex cases, the positioning of affixes may depend simultaneously on the person and number values of the markers themselves, as well as on orthogonal features like TAM, inflection class, polarity, voice, etc. In Fula (Table 4), for example, the position of A/S markers is not only dependent on their person-number values but also on TAM (see also Nepali in Crysmann & Bonami 2016). Notice in Table 4 that the order of the 1sg marker mi with respect to the stem is different in the relative past and in the subjunctive passive. These cases count as infringements of both paradigmatic alignment and featural coherence. We register these cases as two different (although not independent) splits in the same language, (i.e., in the case of Fula, 1sg/2 vs 1pl/3 in the relative past and 2 vs 1/3 in subjunctive passive).
The verb loot- ‘wash’ in two different tenses in Fula (Atlantic-Congo) (Arnott 1970: 191–192). The positional split is different in the relative past than in the subjunctive passive: the 1.sg morph mi follows the stem in the former and precedes the stem in the latter, which leads to two different splits of suffixal and prefixal positional patterns (marked in different shades of grey).
| Relative past passive | Subjunctive passive | |||
| sg | pl | sg | pl | |
| 1. ex | lootaa-mi | min-lootaa | mi-lootee | min-lootee |
| 1. incl | – | lootaa-ɗen | – | lootee-ɗen |
| 2 | loota-ɗaa | lootaa-ɗon | loote-ɗaa | lootee-ɗon |
| 3 | ‘o-lootaa | ɓe-lootaa | ‘o-lootee | ɓe-lootee |
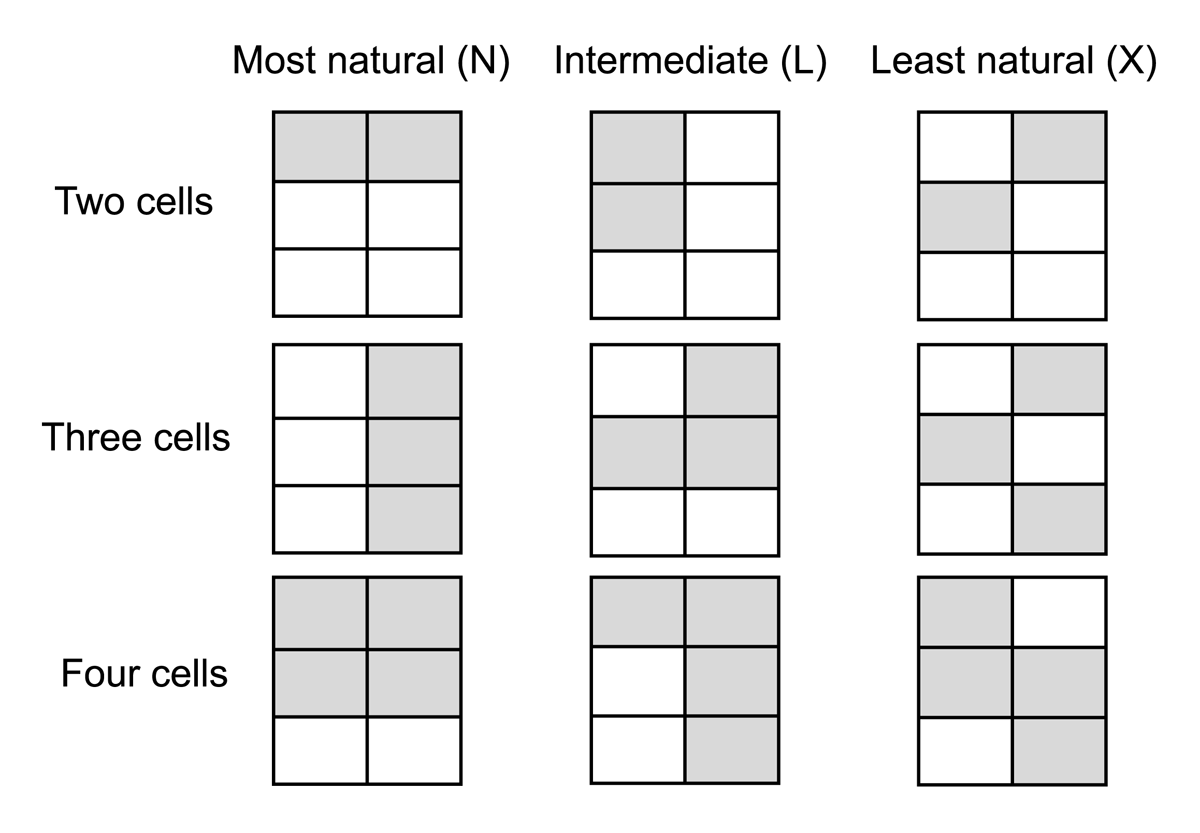
Following the taxonomy in Saldana et al. (2022) we classify positional splits according to their relative degree of naturalness, defined as semantic similarity and computed as the proportion of feature-value overlap between the cells that share identical positional properties. Consider the splits in Table 5. In all three paradigms we can find three person-number cells that share their positional properties. In Gumer (Semitic), 1pl, 2pl, and 3pl are positionally identical, since these values, and no others, are characterised by both a prefix and a suffix. In Koasati (Muskogean), 1pl, 2sg, and 2pl are characterised by being prefixal. In Basque, 1pl, 2sg, and 3pl are all characterised by a prefix and a suffix—note that the 2pl form za-bil-tza-te (which could be glossed as 2-walk-pl/2sg-2pl) has two suffixes rather than one. Following Saldana et al. (2022), these patterns of positional identity will be referred to as N (natural), L (least unnatural, shaped like an L), and X (most unnatural, diagonally arranged) respectively. They are defined as follows for patterns of three cells:
N: All cells in the N-pattern share a value not found elsewhere (e.g. pl in the Gumer case in Table 5).
L: All cells in an L-pattern share a value with some other cell, but not with all other cells (e.g. prefixes in Koasati).
X: In X-patterns, one cell (the 2sg in the Basque example) does not share any value with the other positionally identical cells.5
The verb kft ‘open’ in Gumer (Semitic) (Völlmin 2017: 122), the verb há:lon ‘hear’ in Koasati (Muskogean) (Kimball 1985: 55), and the verb ibili ‘walk’ in Basque (Isolate) (Hualde & De Urbina 2011: 234)
| GUMER Imperfective | KOASATI Active | BASQUE Present | ||||
| sg | pl | sg | pl | sg | pl | |
| 1 | ə-kəft | nɨ-kəft-ɨnə | há:lo-l | il-há:l | na-bil | ga-bil-tza |
| 2 | tɨ-kəft | tɨ-kəft-o | is-há:l | has-há:l | za-bil-tza | za-bil-tza-te |
| 3 | yɨ-kəft | tɨ-kəft-o | há:l | há:l | da-bil | da-bil-tza |
Patterns of two or four cells (see Figure 1) can also be classified into a scale of naturalness comparable mutatis mutandis to that of patterns of three cells. Within a 3×2 person-number paradigm, two cells may lack any shared values (e.g., 1pl, 2sg, type X), share a value also present in other cells (e.g., pl in 1pl, 2pl, type L), or share a value to the exclusion of other cells (e.g., 1 in 1pl, 1sg, type N). Possible four-cell patterns must, in a 3×2 paradigm, necessarily spread over more than one person and number values. However, they will also differ in two respects: 1) as for whether they adopt a distribution with less feature-value overlap (e.g., 1sg, 2sg, 2pl, 3pl: X, 25%),6 or more (e.g., 1sg, 2sg, 3sg, 3pl; 1sg, 2sg, 1pl, 2pl, 33.3%), and 2) as for whether they spread over values present (1sg, 2sg, 3sg, 3pl: L) vs absent (1sg, 2sg, 1pl, 2pl: N) from the rest of the cells.7 Note that this second aspect (i.e., whether or not the feature shared within a pattern is present outside it) is what allows us to classify patterns of two and four cells into three bins of (un)naturalness which can then be compared to the gradient described for patterns of three cells (which do not require reference to this additional second aspect for a three-way classification). Figure 1 displays graphically this naturalness continuum in patterns of two, three, and four cells. Patterns of positional identity smaller than two cells (e.g., Koasati 1sg) cannot be classified into our different degrees of naturalness, so they are irrelevant for our purposes. We also ignore patterns of positional identity larger than four cells because they cannot distinguish different degrees of naturalness in 3×2 person-number paradigms.
Following the degrees of naturalness described for the different types and patterns sizes, and based on the results that Saldana et al. (2022) obtain for similarity-based patterns of syncretism, we expect to find that our most natural N-type positional splits are more probable in natural languages and easier to learn than our L-type, which in turn is expected to be more probable and learnable than splits of the most unnatural type X.
3 Cross-linguistic data
3.1 Data on N, L, and X types of positional splits
Regarding cross-linguistic data, we have two goals. The first one is to assess the recurrence of positional splits. That is, we assess just how (un)common are deviations from the paradigmatic alignment principle introduced in section 2. The second goal is to quantify the probability of occurrence of the different types of splits N, L, and X cross-linguistically, taking into account their expected chance probability.
3.2 Materials and methods
3.2.1 The typological data
We obtained data on the position of person and number agreement markers on the verb from AUTOTYP’s (Bickel et al. 2017) database of grammatical markers. To achieve wider cross-linguistic coverage, we supplemented the data in AUTOTYP with an independent diversity sample: the 100-language sample proposed in WALS (Dryer & Haspelmath 2013). For these additional 100 languages, the same information was registered (i.e., position of A, S, and P-indexing morphology) as was mined from AUTOTYP. The aggregation of these two sources resulted in a sample of 325 paradigms from 227 languages (26 of which had no person or number agreement) from 97 different stocks (i.e., language families of the deepest demonstrable level). Among these, we found 128 paradigms, in 88 different languages from 41 different stocks, that required reference to two or more positions. Remember from Table 4 that a single language can have more than one person-number paradigm with different positional profiles, and hence more than one split. The majority among these (88 paradigms) involve two positions, 18 more involve three positions, 15 involve four positions, six involve five positions, and one six positions.
Figure 2 shows the geographical distribution of the languages in our sample, and which of these have any of the splits of interest. The distribution basically mirrors the increased head-marking and high-synthesis frequencies that have been noted around the Pacific, with outliers in what has been called the Eurasian enclaves (Bickel & Nichols 2013). A second frequency spike characterises the Rift Valley and various branches of Afro-Asiatic in Africa. On a global scale, split patterns are in the minority (39% of languages, 37% of paradigms), which is consistent with the importance of the principle of paradigmatic alignment of morphs and, more generally, of category clustering (Mansfield et al. 2020; 2022). Affixes expressing the same grammatical category (e.g., agreement with A) tend to appear in the same morphological position in the word.
Looking at the presence and absence of positional splits across language families reveals, in addition, that violations of this principle seem to be highly inheritable. Thus, languages from the same family tend to be comparatively homogeneous regarding whether they do (e.g., Algonquian, Kiranti, Afro-Asiatic, Uto-Aztecan) or do not (e.g., Tupi-Guarani, Indo-European, Dogon) display positional splits, and of which type. While it is unknown whether this homogeneity reflects slow rates of change or a diachronic bias favouring certain splits (or both), we take a conservative approach and take phylogenetic relatedness (i.e., language family) as a key control in our data analysis below.
In languages showing positional splits, we acquired further information about the number of positions available to A, P, and S morphs, and the positional properties of all person-number values in the paradigm. Some qualifications are needed regarding how exactly these data were coded in specific cases. First, when the same markers in the same positions index different roles (e.g., A and S as in Armenian, or less commonly, S and P as in Quiche), we counted them only once, that is, as a single paradigm.8 Secondly, we identified a split only in paradigms with at least two positions involved in the expression of person-number information in a paradigm with everything else held constant (i.e., same role, TAM, polarity, inflection class, voice, etc.). Thus, we did not consider paradigms involving only zero vs non-zero markers as split. Even in multiple-position systems, we disregarded patterns whose positional identity derives from the absence of markers, like 3sg/3pl in Koasati in Table 5. We decided to do this because the number and position of morphological zeros is much more subjective and analysis-dependent than that of overt markers. A third clarification concerns the cumulation/separation of person and number. We excluded those positional splits (only four) resulting from separative affixes for person and number: one from Imonda (Seiler 1985) and Acoma (Miller 1965), and two from Wichí (Terraza 2009).
Applying these criteria leaves us with 84 paradigms among the two-position systems—we exclude systems with more available positions because they are too scarce to test their naturalness gradient statistically. We classified all the two, three, and four-cell same-position patterns (141 in total) that these 84 paradigms included into our naturalness types N, L, and X, as defined in section 2 (see also 1). The counts of the positional-splits data collected are summarised in Table 6.
Counts of positional splits of different types and sizes (two position systems only).
| N-type | L-type | X-type | |
| two cells | 23 | 36 | 18 |
| three cells | 8 | 24 | 3 |
| four cells | 13 | 13 | 3 |
3.2.2 Data Analysis
In absolute terms L-type syntagmatic patterns are more common than N-type patterns (Table 6). This seems surprising at first sight. However, the raw numbers need to be interpreted relative to baseline expectations since each type has a different probability of occurring by chance (e.g., there are less logically possible configurations of N-type patterns than L-type patterns). That is, taking as an example 3-cell patterns in a 6-cell person-number paradigm, only two sets of cells are natural (i.e. 1sg/2sg/3sg, and 1pl/2pl/3pl), while twelve are of the L-type (e.g. 1sg/2sg/2pl, 1sg/2sg/1pl, 1sg/3sg/1pl, 1sg/3sg/3pl, 2sg/3sg/2pl, 2sg/3sg/3pl, etc.). In response to these asymmetries we will take into account the baseline probability of each of these type of patterns to correct for the results from our statistical model predicting the likelihood of the cross-linguistic occurrences by pattern type (N-type, L-type and X-type).
3.2.2.1 The baseline
We adopted all the possible combinatorial arrangements as the comparative baseline to assess whether a given pattern type was over- or under-represented cross-linguistically. For our analysis, we only take into account a baseline for 3×2 paradigms and two positions (e.g., before and after the stem). As explained in section 3.2.1, these constitute the majority of our data and thus the only patterns we can test statistically. For each pattern of n number of cells (two, three, or four) within this six cell paradigm, with two possible affixal positions, we generated all possible permutations with replacement. For each of the permutations, we dummy-coded whether or not they contained a pattern of positional identity of type t (N, L or X), excluding zero-marking. The probability of occurrence extracted from this binary variable (i.e., P(N) = 0.126, P(L) = 0.527, P(X)=0.416, for 3×2 paradigms and patterns of 2, 3 or 4 cells) will later be used to correct the posteriors obtained form our Bayesian regression model predicting the likelihood of occurrence of each pattern type in our cross-linguistic data.
A general formula to calculate the baseline probability of a pattern tn (of type t and size n) in a paradigm of size m within a system of s possible affix positions is shown in 1,
- (1)
where:
(n) = size of pattern, i.e., number of cells with the same positional identity.
(m) = size of the paradigm by number of cells.
(s) = number of available positions. In each of them a marker can be either present (1) or absent (0). Therefore, with two available positions, there are 22 = 4 logically possible positional arrangements, e.g. prefixal (i.e., [1,0]), suffixal (i.e, [0,1]), circumfixal (i.e., [1,1]), and ∅(i.e., [0,0]).
(τt,n) = number of possible sub-patterns of the same type t and size n (e.g., there are two 3-cell patterns of the N type in a 2×3 paradigm, i.e., 1sg/2sg/3sg and 1pl/2pl/3pl).
This general formula calculates the chance probability of having some pattern of a particular type (N, L, X) and size (two, three, or four cells), in paradigms of a given magnitude (3×2, 3×3, etc.) and a given number of available positions. Thus, for example, N-type patterns of three cells (tn = N-type3) in a six-cell paradigm (m=6) with two positions (e.g., prefix and suffix) (s=2), have a baseline probability of P(N-type3|m=6, s=2) = 0.053.9 This is the probability we expect by chance for N-type patterns of 3 cells (e.g., Gumer in Table 5) in this type of paradigm. The Koasati pattern in Table 5, in turn, would be P(L-type3|m=6, s=2)= 0.316, and the Basque one P(X-type3|m=6, s=3)= 0.4. Our formula calculates all logically possible positional arrangements of a paradigm (denominator), and how many of them contain a given pattern type (numerator). The resulting ratio, therefore, is the proportion of paradigms that contain a given pattern type. Note that a given 3×2 paradigm can, of course, contain more than a single two or three-cell pattern, and logical incompatibilities exist regarding which of them can co-occur, which are reflected in the baseline.
3.2.2.2 Statistical models
We use R’s brms package (Bürkner 2018) as an interface to Stan (Carpenter et al. 2017) to run Bayesian binomial mixed-effects regression models predicting the occurrence of positional splits in the cross-linguistic data by the type of pattern N, L or X. Our dependent variable is the presence or absence of the given pattern in a 3×2 paradigm (for each of the 84 paradigms in our cross-linguistic data). Languages can be represented with more than one paradigm in the data. As fixed effects, we only include pattern type with three levels (N, L and X) and no intercept. As random effects, we include intercepts for language and stock to control for the relatedness that paradigms have within languages and within stocks. We set a student-t prior for the fixed effects (DF=6, μ=0, σ= 1.5); for the random effects, we set a half-Cauchy prior with scale parameter 10 (McElreath 2016).
The model’s estimates show whether positional splits of a given type in the cross-linguistic data are more or less likely than P = 0.5, which is the chance level the binomial model assumes and does not reflect the empirical baseline probability for either pattern type. The posterior estimates are thus later corrected with the baseline probability calculated as described in section 3.2.2.1. In order to do so, we transform the model’s posterior probability predictions with brms’ scaled inverse logit-link function and subtract the baseline probability from these transformed posterior distributions. Table 7 shows the raw (non-modelled) probabilities for each of the pattern types in our cross-linguistic data and in the baseline.
Proportion of N, L and X patterns of 2,3 or 4 cells in 3×2 paradigms in our cross-linguistic data and on the baseline. Remember that in our cross-linguistic data there are 84 different paradigms containing split patterns and proportions are based on those (i.e., 30/84 for N, 45/84 for L and 14/84 for X).
| N-type | L-type | X-type | |
| data | 0.357 | 0.536 | 0.167 |
| baseline | 0.126 | 0.527 | 0.416 |
3.3 Results
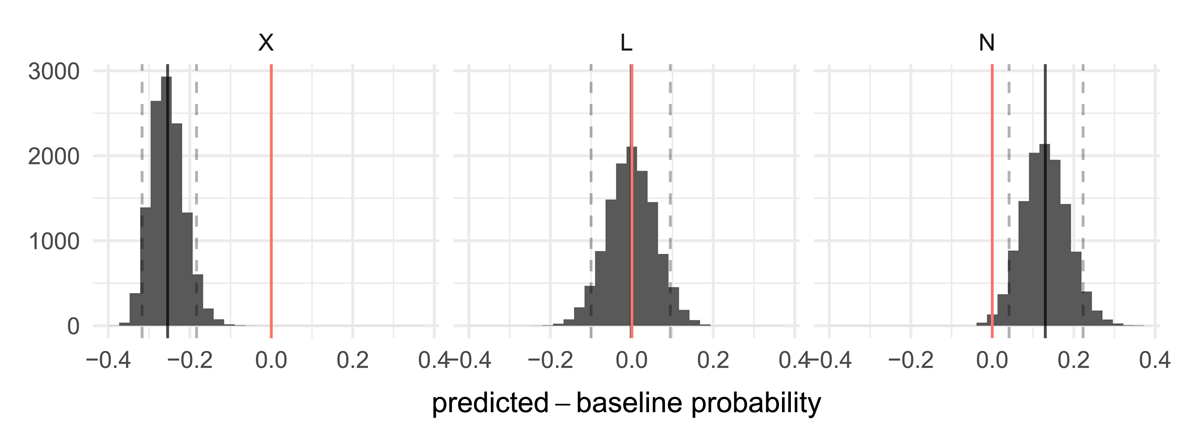
Figure 3 shows the model’s corrected posteriors distributions, with the point mean estimates and 90% credible (equal-tailed) intervals. We find that the most natural patterns N are more likely in the cross-linguistic data that we would predict by chance ( = 0.130, 90%CI= [0.041,0.223]); we find that 99.3% of the posterior samples are above 0 (i.e., P( > 0) = 0.993). The most unnatural X-patterns, in turn, have a below chance probability of occurrence cross-linguistically ( = –0.255, 90%CI = [–0.317,–0.184], P( > 0) = 0). Intermediate-unnaturalness L-patterns occur with a similar probability as expected by chance ( = 0.001, 90%CI = [–0.100, 0.095], P( > 0) = 0.491).
Posterior distribution densities for each pattern type (X, L or N) corrected for their baseline probability (i.e., model predicted probabilities minus the baseline probability). We show the corrected mean point estimates (solid black line) and 90% credible intervals (dashed grey lines). Posterior samples above or below 0 suggest that the patterns occur in the cross-linguistic data above or below chance respectively; posterior samples around 0 suggest that the observed data is at chance.
These results are consistent with the N-type > L-type > X-type gradient that we predicted based on the degree of naturalness of the paradigms. They are also consistent with what has been observed for morphological patterns of syncretism (Saldana et al. 2022). We suggest that the gradient derives from a cognitive bias towards similarity-based structure, that is, towards paradigm partitions where cells behaving in the same way have (1) more feature values in common, and/or (2) more values that are not shared with other cells.
We fitted an additional model with the same structure to test whether we find the same gradient if we considered the degree of semantic similarity (i.e., feature value overlap) exclusively. While taking into consideration the degree of similarity alone does not make any difference for patterns of three cells, it does impact patterns of two and four cells, as L and N patterns have the same similarity scores for those pattern sizes (see section 2). Results from the Bayesian regression model ratify the predicted gradient of occurrence. We find that patterns with a higher value overlap are more likely.
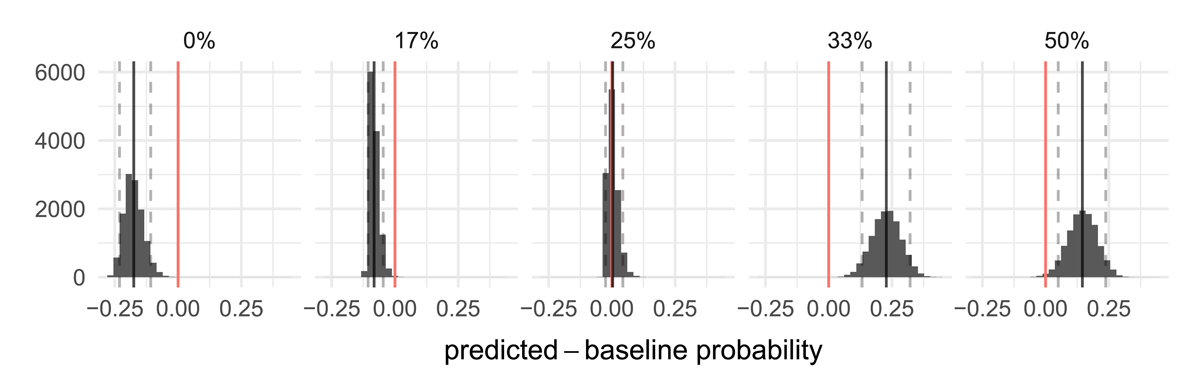
Figure 4 shows the model’s posterior distributions (corrected for their baseline probability) for each group of patterns with a given similarity score. Similarity scores are calculated as the mean feature value overlap across all pairs of cells within a pattern, taking into account the structure presented in Table 2.10 Our model results suggest that the two patterns with higher similarity scores are more likely to occur in our cross-linguistic data than predicted by chance (P( > 0) > 0.99), the two patterns with the lowest similarity scores show a below-chance likelihood of occurrence (P( > 0) < 0.01), and the patterns with with an intermediate similarity score are as likely as predicted by chance (P( > 0) = 0.497).11
Posterior distribution densities for each similarity score corrected for their baseline probability. We show the corrected mean point estimates (solid black line) and 90% credible intervals (dashed grey lines). Posterior samples above or below 0 suggest that the patterns occur in the cross-linguistic data above or below chance respectively; posterior samples around 0 suggest that the observed data is at chance.
In the following section we will probe whether the same bias towards higher semantic similarity, with the same gradient, can also be elicited from adult learners in a controlled setting. We will only focus on testing the differences in the learnability of positional split patterns N, L and X of three cells uniquely—and thus focus on a naturalness gradient based on the degree of semantic similarity alone. To do so, we use artificial language learning experiments (Saldana et al. 2022), assuming that they reflect similar cognitive biases as those that drive asymmetries in cross-linguistic distributions when languages evolve over time and space (Smith et al. 2003; Reali & Griffiths 2009; Culbertson et al. 2012; Saldana et al. 2021a; 2022; Fedzechkina et al. 2012; Kirby et al. 2004; Bickel 2015). The results from artificial language learning experiments with adult learners can help us uncover cognitive biases during the acquisition of patterns of positional splits in an otherwise unattainable controlled setting. The assumption is that the biases that are detectable in such a setting should reflect (at least) some aspects of those active during the learning process involved in language change, and that patterns that are more easily learned by adults will ultimately be more robustly transmitted over time. This assumption is plausible because language change necessitates a stage where new variants (e.g., a new pattern of positional splits) are learned by an increasing number of speakers, mainly adolescents and adults (Blythe & Croft 2021). The evolutionary dynamics of language transmission are in the end shaped by thousands of learning trials, favouring the selection and maintenance of cognitively preferred patterns (Bickel 2015; Smith 2018; Reali & Griffiths 2009)
4 Learnability experiments
We conduct two artificial language learning experiments. In a first experiment we test the learnability of the naturalness gradient natural > L-type> X-type in 3×2 paradigms. And even though the typological data is too scarce to explore any gradient of naturalness in 3×3 paradigms (i.e., those including number:du), we can still experimentally probe their learnability. In a second experiment we thus test the gradient in 3×3 paradigms. Experiment 1 has the advantage of comparability with the cross-linguistic data from section 3, and with the experiments that Saldana et al. (2022) conducted on syncretism. Experiment 2 allows us to explore the naturalness gradient in a more complex morphosyntactic space, and to include an additional degree of unnaturalness (i.e., we test four rather than three degrees: natural > L-type> X-type > XX-type).
4.1 Materials and methods
The two artificial language learning experiments described here are based on Saldana et al. (2022). We use an ease-of-learning paradigm where we train and test participants on a person-number paradigm with a specific pattern of morphological positional splits and compare how accurately they learn them during testing. The only difference between Experiment 1 and 2 is that number is a binary feature (sg and pl) in the former and a ternary feature (sg, pl, and du) in the latter; person remains a ternary feature across experiments (i.e., 1st, 2nd and 3rd). Consequently, paradigms contain 3×2 cells in Experiment 1 and 3×3 cells in Experiment 2. Within each experiment, we run different conditions with verbal paradigms containing positional splits of person-number agreement bundles of varying degrees of (un)naturalness: natural, L-type or X-type patterns.
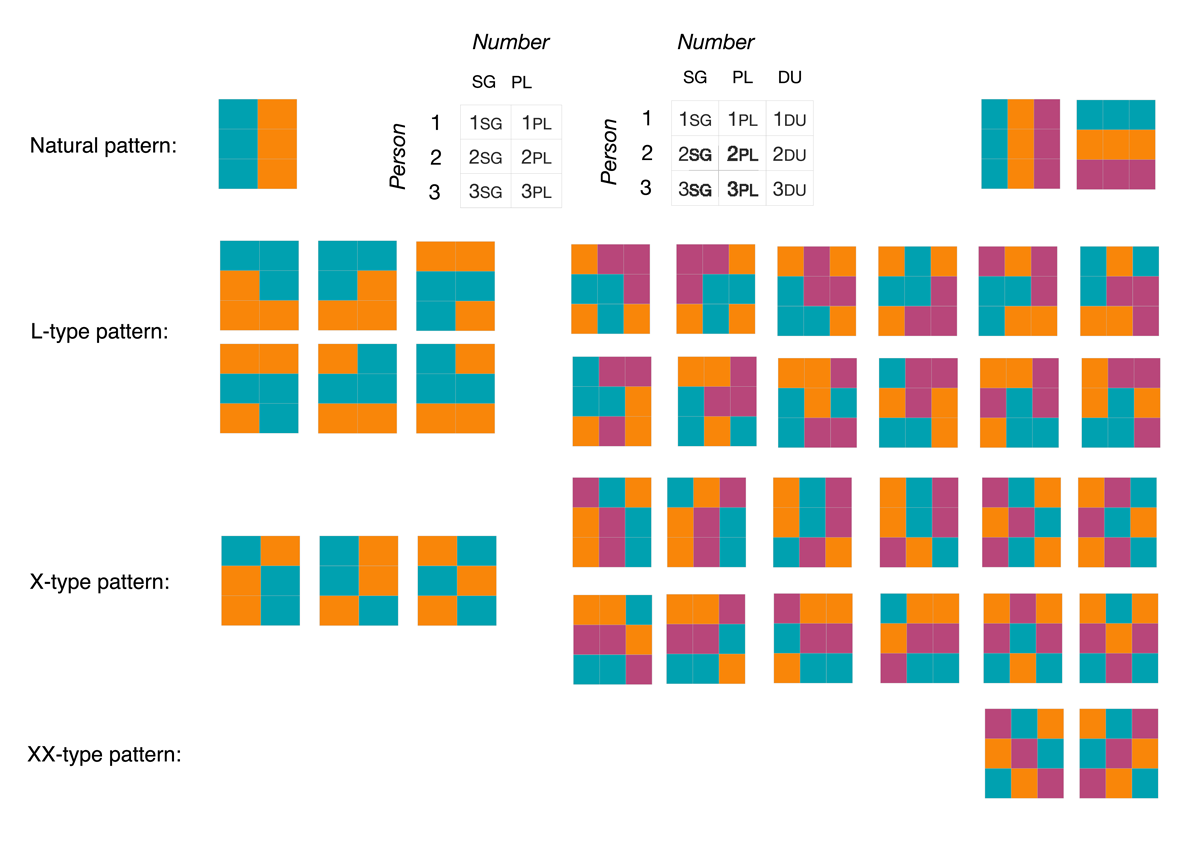
Person-number verbal agreement is marked cumulatively in a single affix and can appear in a different position (e.g., suffixation, prefixation or zero-marking) depending on the person-number feature value bundle. Paradigms contain only two (3×2, Experiment 1) or three (3×3, Experiment 2) different syntagmatic arrangements for agreement markers, each present in half (in 3×2) or a third (in 3×3) of the cells of the paradigm respectively, which partition the person-number space according to the experimental conditions illustrated in Figure 5—where each cell colour represents a different positional arrangement (e.g., suffix, prefix, or ∅).12
Patterns of positional splits within each of the experimental conditions in Experiment 1 (left hand side, 3×2 cell paradigms) and Experiment 2 (right hand side, 3×3 cell paradigms). Each colour represents a different position for the marker in a given cell. In Experiment 1, only suffixes and prefixes are possible, and in Experiment 2, we include three possible arrangements: suffixes, prefixes, and ∅. For example, in the natural pattern of Experiment 1, all singular persons could be marked with prefixes and all plural persons, with suffixes. In the leftmost natural patterns of Experiment 2, all singulars could be marked with ∅, all plurals could be marked with suffixes, and all duals with prefixes.
As illustrated in Figure 5, in Experiment 1 (3×2 paradigms), we have three conditions with positional splits: natural, L-type, and X-type paradigms. Natural paradigms have a different syntagmatic arrangement depending on number (e.g., prefixes for sg and suffixes for pl markers, across all different person values). The L-type paradigms have six different configurations. An example of an L-type pattern could contain suffixes for 1sg, 1pl and 2pl (i.e., 1=2pl) and prefixes for 2sg, 3sg and 3pl (i.e., 2sg=3). The X-type pattern has three different configurations; for instance, it could contain suffix markers for 1sg, 2pl and 3pl and prefix markers for 1pl, 2sg and 3sg. These three conditions in Experiment 1 mirror those tested in Saldana et al. (2022) for patterns of syncretism.
In Experiment 2 (3×3 paradigms), we have four conditions with positional splits: natural, L-type, X-type and XX-type paradigms. Natural paradigms can have a different syntagmatic arrangement for number or for person values. The L-type and X-type patterns can have twelve different configurations each (see Figure 5). The additional, most unnatural condition is where all cells differ in all feature values (possible for 3×3 paradigms but not for 3×2), and we call this the XX-type.
For each experiment, we run a further condition without positional splits. In these no-split conditions, all number-person markers are placed in the same position, that is, either all markers are prefixes or all markers are suffixes. These conditions serve as a baseline for maximum learnability. We expect natural patterns to be closest in learnability to these baseline no-split conditions, L-type patterns to be more difficult, X-type patterns to be more difficult still, and XX-type patterns to be the most difficult.
4.1.1 Participants
We recruited 767 participants through Amazon Mechanical Turk, each randomly assigned to an experimental condition. Participants were all over 18 years old, based in the US and with approval ratings >95%. There were no further requirements for participation aside from successfully completing a series of bot-screening questions to start the experiment, and finishing it in less than 50 and 90 min for Experiment 1 and 2 respectively. Uninterrupted sessions nonetheless lasted up to 15 and 30 minutes for Experiments 1 and 2 respectively. Participants were paid a base rate of $2.5 or $3.5 respectively plus they received a bonus of $0.02 for each correct response. Participants could obtain a bonus reward of up to $1.56 in Experiment 1 (18+60 trials), and $4.32 in Experiment 2 (36+180 trials). We exclude the data from participants who failed to provide at least 80% of correct responses in the final block of vocabulary testing during the training phase. Following this criterion, we excluded 215 participants.13 After exclusions, our analysis thus contains the data from 552 participants in total, 247 in Experiment 1 and 303 in Experiment 2. For Experiment 1, we have 65, 60, 62 and 62 participants in the no-split, natural, L-type, and X-type conditions respectively. For Experiment 2, we have 60, 61, 61, 60, and 60 participants in the no-split, natural, L-type, X-type and XX-type conditions respectively.
4.1.2 The artificial lexicon
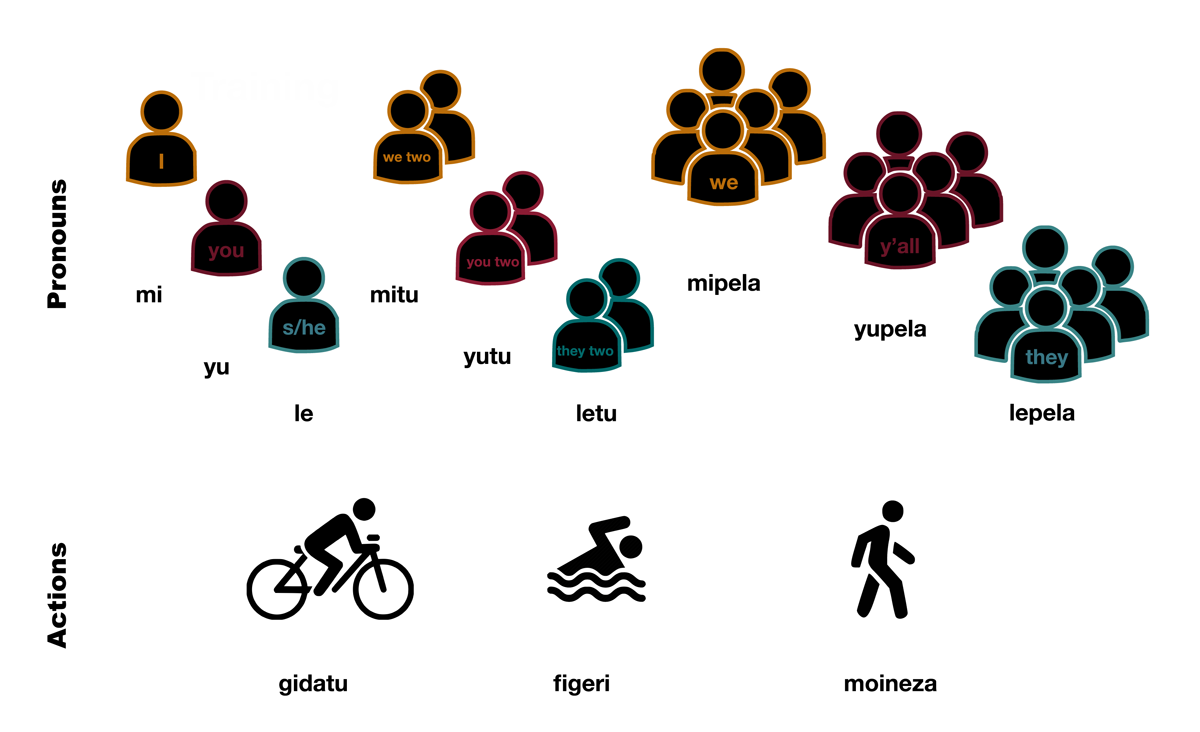
The artificial lexicon in Experiment 1 comprises six pronouns, three lexical verbs and six person-number cumulative agreement markers. The semi-nonce subject pronouns (based on Tok-Pisin, an English-based creole language spoken in Papa New Guinea) are composed of the person morphs mi (1st person), yu (2nd person) and le (3rd person), followed by the number morphs -∅ (sg), and -pela (pl). The semi-nonce lexical verbs (based on Basque) are gidatu, figeri and moineza which correspond to ‘to cycle’, ‘to swim’ and ‘to walk’ respectively. The agreement markers are selected from an array of six CV syllables {na, gu, te, po, ki, so}, and randomly assigned to each of the six person-number bundles. These markers can be either suffixes (in three cells) or prefixes (in the other three cells); these correspond to the colour splits in the experimental conditions shown in Figure 5—note that the prefix/suffix position for each split of three cells is asssigned randomly. In the no-split condition, however, all the agreement markers are either suffixes or prefixes.
The artificial lexicon for Experiment 2 is as per Experiment 1 but with the addition of a dual number. It thus includes nine rather than six pronouns (i.e., additional 1du, 2du and 3du pronouns); these additional dual pronouns are composed of the same person morphs mi (1st person), yu (2nd person) and le (3rd person), followed by the dual (du) morph -tu. The number of verbs and agreement markers is as per Experiment 1. Agreement markers can be either, prefixes, suffixes, or ∅. Because three paradigm cells have ∅ agreement, we only require six person-number overt markers just as in Experiment 1, three of which are prefixes, and the other three, suffixes (see Figure 5). In the no-split condition, however, we have nine markers (from the following array {na, gu, te, po, ki, so, pa, lu, ze}, one for each cell) and all of them are either prefixes or suffixes.
4.1.3 Experimental procedure
The experimental procedure is divided into two phases. In the first phase, we train and test participants on the artificial lexicon without verbal agreement, that is, only on the pronominal forms and the uninflected lexical verbs (i.e., in isolation, without agreement affixes). In each training trial, participants see an image of an action or a pronoun, and their corresponding forms in the artificial language (as shown in Figure 6). In each testing trial, participants are shown an image and are asked to select the corresponding form in the artificial language out of an array of two, that is, the target, and a randomly selected form of the same lexical category (pronoun or verb) as the target. They receive feedback after each selection and a bonus of $0.02 for each correct response. Participants see each mapping three times during training, and twice during the vocabulary testing in Experiment 1 (across two blocks of all nine lexical items each), or thrice in Experiment 2 (across three blocks of all 12 lexical items each).
Visual stimuli used to teach and illustrate the actions and pronouns along with their corresponding descriptions (i.e., uninflected verbs, and pronouns respectively). All of these were included in Experiment 2, where we included dual number but not in Experiment 1, where we only implement a binary number feature (i.e., with sg and pl uniquely).
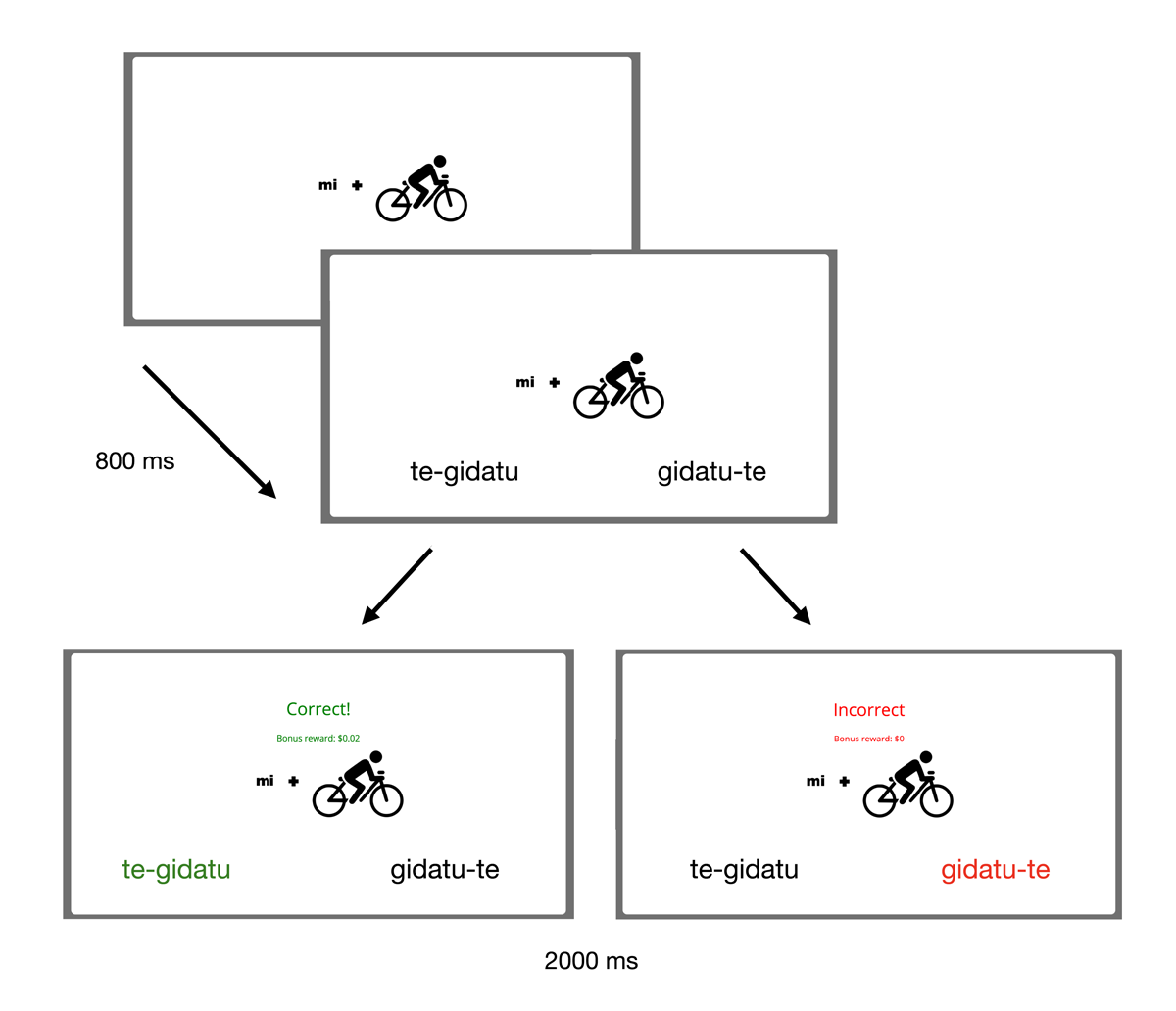
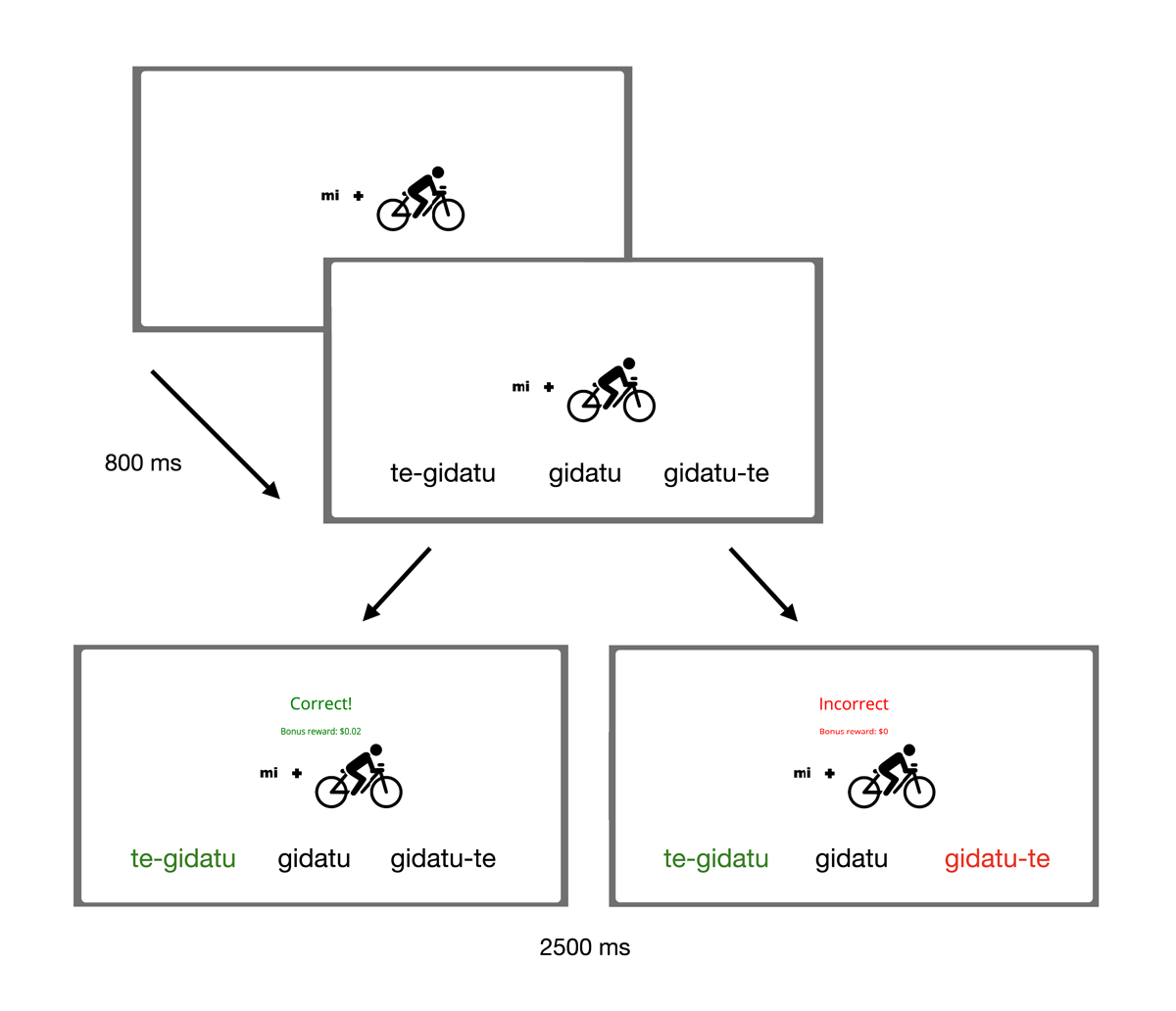
In the second and critical phase, we train and test participants on the verbal paradigms with the agreement affixes. For this phase, we use feedback learning whereby training and testing are simultaneous. In each trial, participants see an image combining a pronoun and an action and after 800 ms, two (Experiment 1) or three (Experiment 2) verbal forms are displayed with the same stem and affix form, but in different positions. Participants have to select which form they think is the one that corresponds to the specific pronoun+action combination, in other words, they have to select the verbal form they think agrees in person and number with the given pronoun. They receive feedback on their selection so they can learn the correct correspondence as they move along testing. In Experiment 1, participants are only told whether their selection is correct or incorrect; if they select the incorrect form, they know that the correct one is the only other form (see Figure 7 for an illustration of a complete critical test trial in Experiment 1). However, in Experiment 2 there are three alternatives, so if participants select the wrong one, they cannot know which one is the correct one straightaway; we thus add feedback about the correct form when participants select the incorrect form to facilitate learning (see Figure 8 for an illustration of a complete critical test trial in Experiment 2). As in the previous phase, participants receive a bonus of $0.02 for each correct response. This phase comprises 10 blocks of six trials in Experiment 1 and 20 blocks of nine trials in Experiment 2; each block contains all different person-number agreement combinations (i.e., the whole verbal paradigm, but with randomly chosen verb stems at each trial).14
Example test trial in the critical phase of Experiment 1. Participants are shown an image of a pronoun+action combination and after 800ms were asked to select the corresponding inflected (verb-affix) form of the verb in the artificial language out of an array of two. They are provided with feedback after they submit their response. The feedback displays whether their choice is correct as well as the bonus amount accumulated so far in the experiment (and it remains on screen for 2000 ms). The feedback allows participants to learn the correspondence between the position of the affixes and the person-number feature values as they move along testing.
Example test trial in the critical phase of Experiment 2. Participants are shown an image of a pronoun+action combination are asked to select the corresponding inflected (verb-affix) form of the verb in the artificial language out of an array of three. The feedback they receive after they submit their responses displays whether their choice is correct and the bonus amount accumulated so far in the experiment (which remains on screen for 2500 ms); for incorrect responses, participants are also told which is the correct form out of the three.
4.1.4 Data analysis
4.1.4.1 Preregistered Confirmatory Analysis
We use R’s brms (Bürkner 2018) as an interface to Stan (Carpenter et al. 2017) to run a Bayesian binomial regression model predicting participants’ performance by condition and test block. We run separate models for Experiments 1 and 2, with the same model structure.
Our dependent variable is participants’ responses for each of the critical test trials (coded as 1 if correct, and 0 if incorrect). As fixed effects, we include Condition, Block, and their interaction. Block is coded as a centered continuous variable, and we interpret its slope as the learning rate. We apply Helmert contrast coding to the categorical predictor of Condition. In Experiment 1 we compare L-type to X-type, natural to the average of the two, and no-split to the average of all the rest. In Experiment 2, we compare X-type to XX-type, then L-type to the average of the two, Natural to the average of the previous three levels, and No-split to the average of all other levels.15 As random effects, we included intercepts for participants as well as by-participant slopes for the effect of Block.
We set the same student-t prior on all fixed effects as well as on the intercept (DF=6, μ=0, σ= 1.5) (Kurz 2019); for the random effects, we set a half-Cauchy prior with scale parameter 10 (McElreath 2016). Further details on all models reported in this paper can be found in the analysis script available in osf.io/hy76j/.
4.1.4.2 Non-preregistered Exploratory Analysis
Following Saldana et al. (2022), we explored the learnability of individual cells within L-type patterns. We fitted a Bayesian binomial regression model predicting participants’ performance by cell type and testing block. Cell type is a three-level categorical variable as there are three cells in each of the positional arrangements within a paradigm: one type of cell only overlaps by number value with another cell (called here cells connected by number, e.g., the 2sg in 1sg, 2sg, 1pl or pink cell in  ), another type of cell only overlaps by person value (cells connected by person, e.g., the 1pl in 1sg, 2sg, 1pl or red cell in
), another type of cell only overlaps by person value (cells connected by person, e.g., the 1pl in 1sg, 2sg, 1pl or red cell in  ), and the third type of cell overlaps with the other two cells, one by number value and another by person value (connecting cells, e.g., the 1sg in 1sg, 2sg, 1pl or blue cell in
), and the third type of cell overlaps with the other two cells, one by number value and another by person value (connecting cells, e.g., the 1sg in 1sg, 2sg, 1pl or blue cell in  ). For each L-type paradigm in Experiment 1, there are two cells of each type (e.g.,
). For each L-type paradigm in Experiment 1, there are two cells of each type (e.g.,  ); in Experiment 2, there are three cells of each type. Our dependent variable is participants’ responses for each of the 60 critical test trials (coded as 1 if correct, and 0 if incorrect). As fixed effects, we include Cell type as well as Block and an interaction term. The categorical predictor Condition is Helmert contrast-coded so we compare cells connected by person to those connected by number, and the connecting cells to the average of the two; Block is coded as a centered continuous variable. As random effects, we included intercepts for participants as well as by-participant slopes for the effect of Block and Cell Type. We use the same priors as in the confirmatory models.
); in Experiment 2, there are three cells of each type. Our dependent variable is participants’ responses for each of the 60 critical test trials (coded as 1 if correct, and 0 if incorrect). As fixed effects, we include Cell type as well as Block and an interaction term. The categorical predictor Condition is Helmert contrast-coded so we compare cells connected by person to those connected by number, and the connecting cells to the average of the two; Block is coded as a centered continuous variable. As random effects, we included intercepts for participants as well as by-participant slopes for the effect of Block and Cell Type. We use the same priors as in the confirmatory models.
4.2 Results
4.2.1 Learnability gradient of (un)natural patterns of positional splits
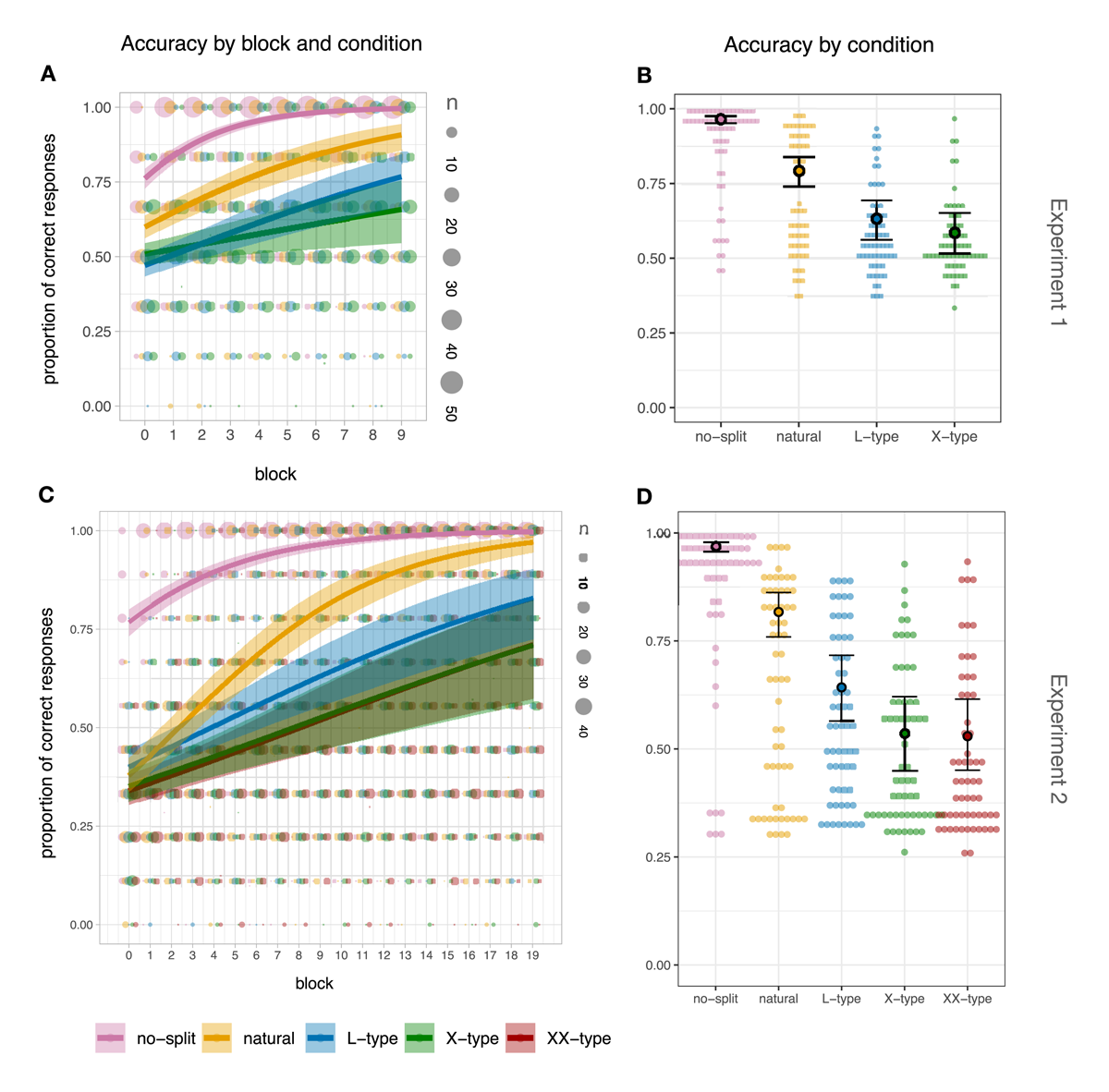
Based on our hypotheses, we predict X-type paradigms to be the least learnable, followed by L-type, natural, and no-split paradigms. Figure 9 shows participants’ accuracy scores and the Bayesian model’s predicted means for Experiments 1 and 2 respectively: Figure 9A and 9C show the accuracy by block as well as condition and Figure 9B and 9D show the overall accuracy across all 60 trials by condition. A visual inspection of the results suggests the predicted gradient of learnability no-split > natural > L-type > X-type across experiments. We observe no difference, however, in the learnability of X-type and XX-type patterns in Experiment 2.
Accuracy scores in Experiment 1 (top, 3×2 paradigms) and 2 (bottom, 3×3 paradigms. (A&C) Accuracy by testing block for each of the four conditions. Shaded dots represent participants’ individual scores, and larger dots represent more individuals as per the legend; thick lines represent the model’s predicted accuracy means conditioned on experimental condition and block. The shaded area shows the 90% credible intervals. (B&D) Overall accuracy by condition. Shaded dots represent participants’ individual scores; black-circled dots represent the model’s predicted mean accuracy scores conditioned on experimental condition, and the error bars represent the model’s predicted 90% credible intervals.
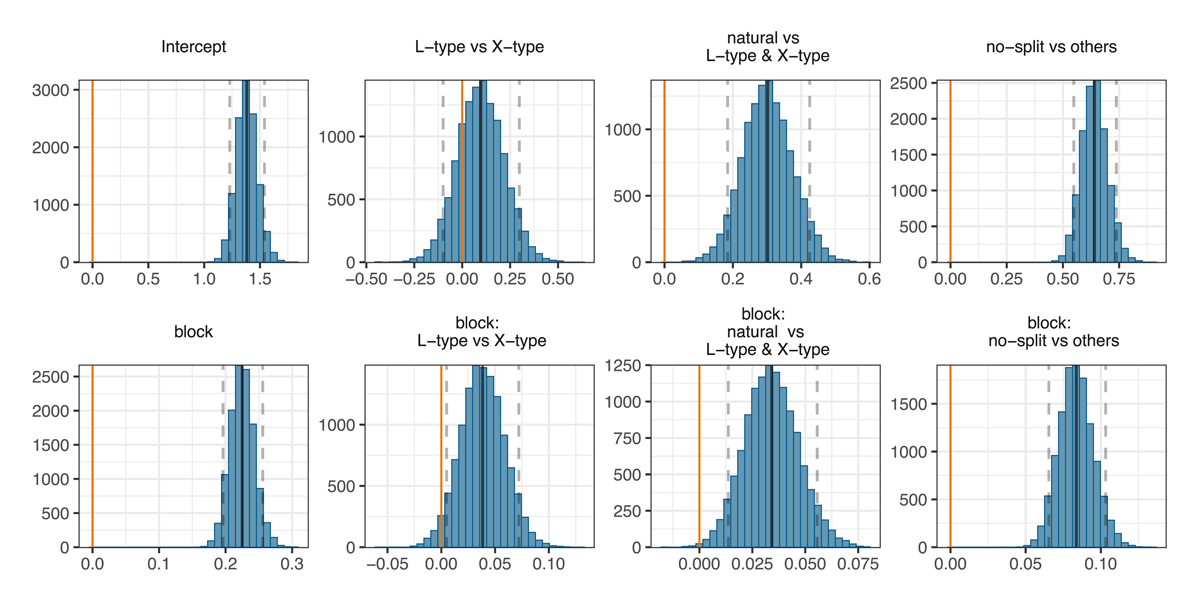
Results from the Bayesian binomial regression models largely confirm our predictions. Figure 10 shows Experiment 1 model’s posterior probability distributions for all fixed effects along with their means (solid grey lines) and 90% credible intervals (dashed grey lines).16 We find that accuracy scores for L-type and X-type are similar half-way through the experiment ( = 0.097, 90%CI = [–0.100, 0.298], SE = 0.122, P( > 0) = 0.786) but they increase more by block in L-type than in X-type ( = 0.038, 90%CI = [0.005, 0.072], SE = 0.021); 97% of the posterior samples are above 0 (i.e., P( > 0) = 0.970) thus making it highly probable that L-type paradigms are learned faster than X-type paradigms, although the difference is relatively small. We also find that natural paradigms show both higher accuracy scores ( = 0.302, 90%CI = [0.185, 0.425], SE = 0.073, P( > 0) = 1) and faster learning rates ( = 0.034, 90%CI = [0.014, 0.056], SE = 0.013, P( > 0) = 0.998) than L and X-type paradigms. Further, no-split accuracy scores are overwhelmingly higher ( = 0.640, 90%CI = [0.548, 0.738], SE = 0.058, P( > 0) = 1), and the learning rates are faster ( = 0.084, 90%CI = [0.065, 0.103], SE = 0.011, P( > 0) = 1) than the average of all other conditions.
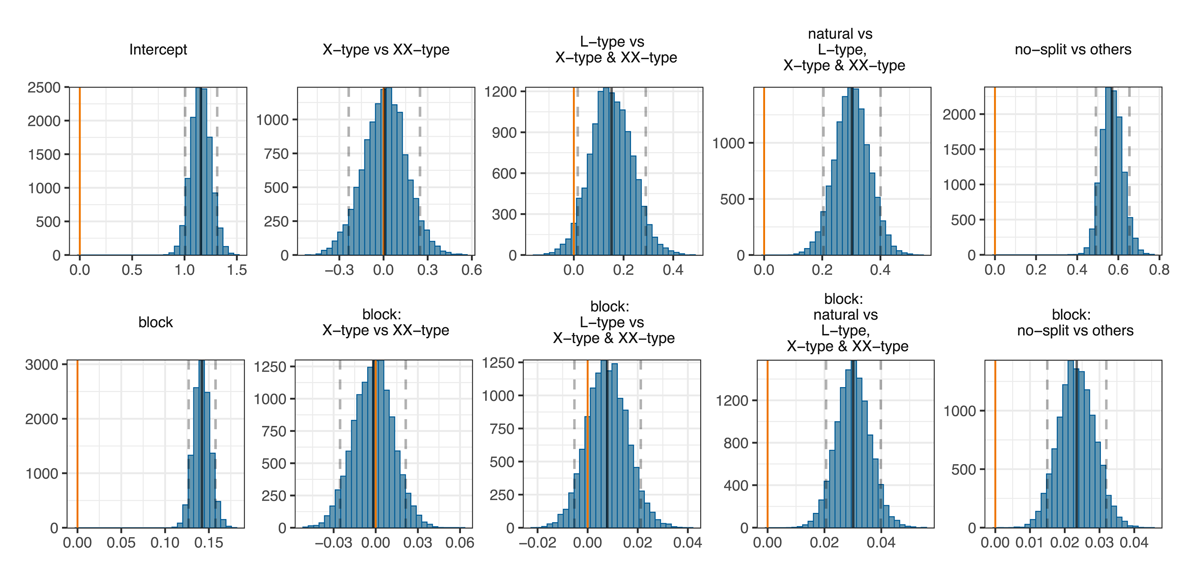
Figure 11 shows the results form the model fits of Experiment 2. We found no difference between X-type and XX-type; neither in accuracy at the intercept ( = 0.015, 90%CI = [–0.222, 0.250], SE = 0.142, P( > 0) = 0.545) nor in the learning rate ( = –0.001, 90%CI = [–0.024, 0.022], SE = 0.014, P( > 0) = 0.472). However, we did find higher accuracy scores in L-type than in X-type and XX-type ( = 0.151, 90%CI = [0.014, 0.292], SE = 0.085, P( > 0) = 0.965). The learning rate does not seem to diverge as much, as we only find relatively weak evidence for a slight advantage of L-type over X-type and XX-type ( = 0.008, 90%CI = [–0.006, 0.022], SE = 0.008, P( > 0) = 0.828). As in Experiment 1, we also found that natural paradigms show both higher accuracy scores ( = 0.305, 90%CI = [0.207, 0.407], SE = 0.061, P( > 0) = 1) and faster learning rates by block ( = 0.030, 90%CI = [0.021, 0.040], SE = 0.006, P( > 0) = 1) than unnatural paradigms, and that no-split accuracy scores (and their increase by block) are also overwhelmingly higher ( = 0.568, 90%CI = [0.489, 0.648], SE = 0.048, P( > 0) = 1; = 0.023, 90%CI = [0.015, 0.032], SE = 0.005, P( > 0) = 1) than the average of all other conditions.
4.2.2 Learning strategies in L-type patterns
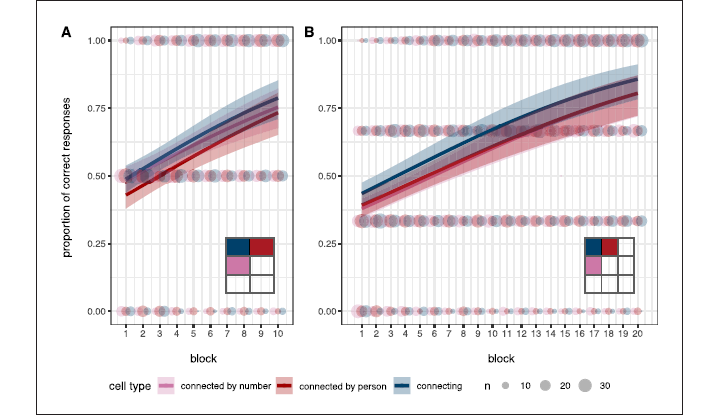
Saldana et al. (2022) showed that the difference in learnability between L-type and X-type patterns of syncretism was not driven by any preference for a specific pattern or sub-pattern within L-type patterns. Instead, it seemed derived from the fact that participants learned connecting cells in L-type patterns (i.e., those that share a feature value with each of the other two cells of a syncretic pattern; blue in  ) earlier than any other individual cell type. Connecting cells are learned better because they form natural sub-patterns with each of the other cells. Consistent with a bias towards similarity-based structure, the connecting cells act as an anchor of the similarity relations within the L-type patterns. In Experiment 1 and 2 we replicate these results for positional split patterns: connecting cells reach higher accuracy scores overall (see Figure 12).
) earlier than any other individual cell type. Connecting cells are learned better because they form natural sub-patterns with each of the other cells. Consistent with a bias towards similarity-based structure, the connecting cells act as an anchor of the similarity relations within the L-type patterns. In Experiment 1 and 2 we replicate these results for positional split patterns: connecting cells reach higher accuracy scores overall (see Figure 12).
Accuracy by cell type in L-type paradigms and predicted estimates from the Bayesian binomial regression model in Experiment 1 (A) and 2 (B). Shaded dots represent participants’ individual scores, and larger dots represent more individuals; thick lines represent the model’s predicted accuracy means conditioned on experimental condition and block, and the shaded area shows the 90% credible intervals.
The results from the binomial regression model fit for Experiment 1 suggest that accuracy is higher for connecting cells than for the average across the other cell types ( = 0.062, 90%CI = [0.009,0.116], SE = 0.033, P( > 0) = 0.972). We further found an effect of block suggesting that accuracy increased as participants progressed through the testing phase ( = 0.143, 90%CI = [0.100,0.187], SE = 0.027, P( > 0) = 1). This increase is comparable across cell types (max P( > 0) = 0.683). The model fit for the data in Experiment 2 is very similar. We find that accuracy is highest for connecting cells ( = 0.096, 90%CI = [0.057,0.137], SE = 0.025, P( > 0) = 1), and that accuracy increases by block ( = 0.102, 90%CI = [0.077,0.128], SE = 0.016, P( > 0) = 1) comparably across cell types max P( > 0) = 0.858).
5 Discussion
5.1 A naturalness gradient in paradigmatic splits
This paper explores, with both cross-linguistic and artificial language data, a naturalness gradient in the cross-linguistic recurrence and learnability of positional splits. In contrast to the dichotomous natural vs unnatural distinction in much of the literature, our results concur with other recent research (Herce 2020; Saldana et al. 2022) in identifying naturalness as a matter of degree. According to definitions of naturalness that rely on the sharing of distinctive values (e.g., Bierwisch 1967; Harley & Ritter 2002; Round & Corbett 2017; and see Mielke 2004 regarding phonology), a set of cells will either be, or not be a natural class, depending on whether they share some feature value (e.g., +speaker, -addressee or +singular) to the exclusion of all other cells. Instead, we posit a scale N > L > X, defined by their decreasing degree of naturalness. Naturalness is defined as the proportion of shared feature values.17
Learning morphology or an ordering rule is easiest when they apply over a set of contexts sharing the same value (e.g. 1sg, 2sg and 3sg in the person-number paradigms explored here). Saldana et al. (2022) show this to be the case for syncretic morphological exponents, and the present paper shows the same principle at work in position assignment (Figure 9). This might explain why natural patterns are the most widespread ones cross-linguistically relative to their chance-expected prevalence (see Figure 3). When a set of morphosyntactic contexts falls short of this full naturalness, a higher degree of value overlap (i.e., type L, relative to type X) correlates with a higher cross-linguistic probability, and with higher learnability in experimental settings.
The implications of these results are manifold. First, they ratify the relevance of naturalness and semantic similarity in grammatical (and morphological) architecture (Bierwisch 1967; Baerman et al. 2005; Pertsova 2014), a fact which has been recently challenged. Thus, for example, (Blevins forthcoming) suggests that “the contrast between ‘natural’ and ‘unnatural’ classes appears to reflect a priori assumptions about descriptive ‘economy’ and ‘naturalness’ which have never been shown to be relevant to language structure, acquisition or use.” Our results are not compatible with this assessment. The fact that seemingly unnatural structures exist in some languages, and the fact that these are sometimes productive and robustly transmitted (e.g., in Romance, Maiden 2018), should not detract from the fact that (more) natural ones are nonetheless preferred in cross-linguistic probability and learnability.
Second, our results with respect to the ‘unnatural’ types L and X replicate the learnability and cross-linguistic probability asymmetries found by Saldana et al. (2022) in the domain of whole-word morphological syncretism. That the same gradient applies to very different morphological phenomena suggests that it is driven by a general cognitive bias (Culbertson & Kirby 2016). While whole-word syncretism might be plausibly affected by competing biases like expressivity (i.e., to minimise ambiguity in the encoding of the different values of person and number), the present findings are largely orthogonal to the discriminability of the different values. For example, both Baure and Fula in Table 1 express all combinations of person and number unambiguously. They differ only in whether or not the expression is split between positions. Positional properties of different values concern (more clearly than syncretism) just the ability of language users to generalise over different sets of contexts, with no impact on discriminability or communicative expressivity. We find that, even when a given property or rule, like affix order, contributes little or nothing to the expressivity of a paradigm, (more) natural classes are still preferred. We have shown that this applies to both the cross-linguistic probability of the different naturalness degrees (Section 3), as well as to their learnability in artificial language learning experiments (Section 4). A cognitive bias towards similarity-based structure, which favours more natural patterns, might therefore shape the evolution of paradigmatic structures when languages change in time and space, leading to different probabilities in extant languages.
We have considered L patterns as more natural than X throughout this paper because they have a greater proportion of values shared by their cells (33.3% for L, 16.6% for X). The question remains, however, whether this is the (gradient) factor that motivates this asymmetry. We need to ask what the learning strategy is that language users follow to learn L patterns better than X patterns. In syncretisms within a 3×2 paradigm, Saldana et al. (2022) found that the connecting cell in L (i.e., the one that shares values with all other cells in its pattern, blue in Figure 12) is learned better. We replicate this preference in this paper as well (see Table 12). In L patterns, this cell shares a value with the other two cells and can be understood to behave as a semantic centre to the category; a centre that is missing from X. However, the presence of structural consistency across number for some person values in L but not in X in 3×2 paradigms,18 suggests that factors other than value overlap might also be driving the preference for L. Evidence for such an additional driver is provided in Saldana et al. (2022), who found a slightly enhanced learnability for connected-by-person cells within patterns of syncretism (which lead to the underspecification of the number feature for a given person value). However, contrary to Saldana et al. (2022), we found no learnability advantage here in 3×2 paradigms for the cell connected by person. At the same time, in 3×3 paradigms—where cells connected by person never spread across all number values—we found that the connecting cell was still significantly easier to learn than connected cells, thus confirming the connecting cell’s ancillary role as a category centre within the pattern. This allows us to conclude that structural consistency across all cells with a particular person or number value is not the factor driving the preference for L over X. Instead, it seems to be the higher feature value overlap of L-pattern (connecting) cells that drives this type’s enhanced learnability, which supports our understanding of naturalness and the similarity-based structure bias as a gradient, rather than a dichotomous, preference for more natural patterns.
It needs to be acknowledged that we did not find a significant learning advantage of X over XX, and this runs against the similarity-based structure bias that accounts for the rest of our results. We do not believe, however, that this undermines the postulated naturalness gradient. We rather think that the lack of difference in learnability and learning rates between X and XX is mainly due to the intrinsic difficulty of these patterns. Because X and XX patterns are the most dispreferred, we expect any difference between them to be very hard to detect. This is plausible because the learnability difference heavily decreases already from N vs L (Figure 9) to L vs X, leading us to expect a yet smaller hard-to-detect difference between X and XX. This observation could in fact motivate an additional interpretation of our findings: there does not seem to be a linear, but an exponential gain in learnability given progressively higher degrees of feature-value overlap. This non-linear association between naturalness and learnability could well be the reason that categorical approaches to naturalness have been widespread and often seemingly successful.
5.2 Relation to category clustering and other related biases
Positional splits (of any kind) are a minority, although by a relatively narrow margin (found in 39% of languages, and 37% of paradigms regarding the A, S, and P agreement morphs surveyed here). This might be so because split systems violate another cognitive bias, category clustering (Mansfield et al. 2020; 2022), which privileges the accumulation of similar categories in unique and featurally consistent positions. Phenomena like multiple (Caballero & Harris 2012) and distributed exponence (Carroll 2022), as well as the positionally-split systems we analyse in this paper, constitute deviations from this simpler one-to-one mapping between roles and positions. What our present findings suggest, in addition, is that violations of such preferred configuration are not random but subject to a cognitive bias themselves, the similarity-based structure bias.
The relation between the category-clustering and the similarity-based-structure biases is not straightforward. Our interpretation is that a category-clustered (i.e., no split) system is the optimal configuration, and most frequent result of the similarity-based-structure bias. A no-split system where all A markers appear in one position and all P markers appear in a different one maximises the match between positions and roles. Analogously, a system with a natural split where sg markers appear in a different position from PL markers maximises the match between positions and number values. However, even when a pattern falls short of this (L, X), more similarity (L) between a pattern’s component cells is also associated to higher cross-linguistic probability and higher learnability.
Although the positionally split systems we have focused on here run against category clustering in a narrow sense, they might also bear witness to its preferred status in a different way. If positional splits are regarded as deviations from a preferred configuration where all person-number values of the same argument are expressed in a single position, then we should expect this to be reflected in the cross-linguistic frequency of different pattern sizes. That is, paradigms where most person-number values are marked in the same place should be more frequent than those where there is greater variation because they are closer to being category-clustered. The number of positional split patterns of different sizes shown in Table 8 suggests that this might be the case: four-cell patterns are over-represented relative to two and three-cell patterns.
Overall count (and proportion) of empirical and baseline data for two, three, and four-cell patterns.
| Counts (Proportion) | |||
| Type | Two cells | Three cells | Four cells |
| cross-linguistic data | 77 (0.55) | 35 (0.25) | 29 (0.20) |
| baseline | 2430 (0.64) | 1080 (0.29) | 270 (0.07)) |
Leaving aside the naturalness types that constitute the main focus of this paper, we also explored the positional properties of agreement paradigms to assess which values tend (not) to share their positional properties. This provides independent evidence on the extent to which positional splits reflect morphosemantic structure. Considering the positional properties of the different person-number values across all the paradigms in our sample, we can count how often any two values (e.g., 1pl and 3pl) show different positional properties. Because some languages in our sample are related, and some are more closely related than others, we need to correct our raw counts for this lack of independence. Table 9 corrects for this with phylogenetically weighted proportions (Round 2021) and shows that the most positionally similar values are 1sg/2sg which are distinct 62 times in our sample, or 43.51% of the (weighted) times, followed by 1pl/2pl, 2sg/2pl, 2sg/3sg, 1sg/3sg, and 1sg/1pl. All of these are pairs of cells that share a value. The most positionally dissimilar values, on the other hand, are 3sg/2pl (113 times different in our sample, or 86.95% of the times), followed by 1sg/2pl, 1pl/3pl, 3pl/1sg, and 3pl/2sg. All of these pairs of cells except for one do not share values. Positional affinities and differences, therefore, reveal a trend—driven by a similarity-based-structure bias—for forms with shared values to be positionally more similar. Positional affinities appear to run overall parallel to the structure of person-number feature values. They further contribute to the literature on the architecture of person as a feature (e.g., Harbour 2016; Aalberse 2007; Wyngaerd 2018) by pointing towards the greater affinity of speech-act participants (1/2) over other person combinations (i.e. 2/3 and 1/3).
Proportion of different positional properties between the different person-number values
| 1sg | 2sg | 3sg | 1pl | 2pl | |
| 2sg | 0.4351 | ||||
| 3sg | 0.6271 | 0.6226 | |||
| 1pl | 0.66 | 0.6563 | 0.7432 | ||
| 2pl | 0.8227 | 0.5954 | 0.8695 | 0.4924 | |
| 3pl | 0.7761 | 0.7315 | 0.6311 | 0.803 | 0.7142 |
Also with regard to the positional properties of the different person-number values, it might be interesting to note that 3 tends to use fewer positions than 2 and 1. At the same time, pl values tend to use more positions than sg ones, and they also tend to be expressed/indexed later on average within the word (i.e., suffixally, rather than prefixally). These findings are summarised in Table 10, again reporting phylogenetically weighted proportions.
Positional properties of the different person-number values
| 1sg | 2sg | 3sg | 1pl | 2pl | 3pl | |
| Average number of positions | 1.045 | 1.103 | 0.717 | 1.519 | 1.622 | 1.293 |
| Average position | –0.484 | –0.6202 | –0.1227 | 0.2644 | 0.2868 | 0.4706 |
These tendencies, similar to those found regarding the segmental length of markers (Seržant & Moroz 2022), could provide a window into the idiosyncrasies of positionally split systems and their emergence. Table 10 presents preliminary quantitative evidence for a few things that have been noted in the literature. The first is the tendency for languages to mark 1 and 2 more robustly (i.e., in more positions in this case) than 3 (Watkins et al. 1969; Bickel et al. 2015), and pl more robustly than sg. The second is that the suffixing preference that has been proposed for bound morphology in general (see e.g., Cutler et al. 1985) does not seem to apply to the domain of person marking (notice that the average position for singular person values is below 0, i.e., prefixal, in Table 10). This confirms findings in (Cysouw 2003: 31), who also found a related generalisation that prefixal person-number agreement morphology is prone to horizontal syncretisms (i.e., no number marking) which are often resolved by means of (number) suffixes. Languages like Turkana, Georgian, Basque, Muna, Ayoreo, Tapieté, etc. use a suffixal marker in those plural values that would be otherwise homophonous with the sg. A bias towards homophony avoidance (Song & White 2022; Trott & Bergen 2022), together with a formal markedness of pl (vs sg) could potentially explain the tendency found in this paper for plural values to be associated to more and later positions within the word. This might explain the findings in Trommer (2003), where it is shown that in cases of more-or-less separative marking of person and plural number, the latter marker occurs almost unexceptionally in a later position, regardless of the affixes’ order with respect to the stem (cf. Maldonado et al. 2020).
In sum, this paper’s findings have implications regarding the descriptive and theoretical analysis of affix order (Noyer 1992; Aronoff & Xu 2010), the interface between paradigmatic and syntagmatic complexity (see, e.g., Good 2015), the feature structures and hierarchies of person and number (e.g., Harbour 2016; Aalberse 2007; Wyngaerd 2018), the relationship between the morphological form and the position of affixes (Stump 2001; Spencer 2003; Crysmann & Bonami 2016), and, most importantly, with respect to the conceptualisation and formalisation of (un)naturalness as a gradient property.
6 Conclusion
This paper has explored positional splits in human languages. These are cases where information about “the same thing” appears in different positions within the word. Taking the morphology of person/number agreement in the verb as a test case, we have explored to what extent such splits are natural in the sense that they reflect “natural” overlaps in feature values. We found that, cross-linguistically, positional splits are less frequent than non-split systems (slightly under 40%). Within split systems, those with a higher degree of naturalness, that is, more overlap in feature values, are more probable cross-linguistically relative to what is expected by chance. That is, patterns where values marked in the same position share more meaning (e.g., 1pl, 2pl, 3pl, all sharing pl) are cross-linguistically more probable than those where they share less or no meaning (e.g,. 1pl, 2sg, 3sg). Relying on a sample of 325 paradigms from 227 languages we found that the most natural ones were decisively over-represented when compared to what is expected by a chance baseline of logically possible arrangements. Meanwhile, the most unnatural ones were significantly underrepresented, and intermediate naturalness splits occurred at around chance levels.
Parallel to this, we conducted artificial language learning experiments to probe the learnability of such splits across different degrees of naturalness. The experimental results provide a striking parallel with the cross-linguistic data, with non-split systems easiest to learn, natural positional splits (i.e., sg vs pl) easier to learn than intermediate naturalness splits (e.g., 1sg/3 vs 1pl/2), and these easier to learn than low naturalness splits (e.g., 1sg/2pl/3pl vs 1pl/2sg/3sg).
Together, our findings constitute a successful replication of the naturalness gradient N≫L>X proposed in Saldana et al. (2022), suggesting that it is robust both in terms of cross-linguistic probability and learnability. This supports the notion that the gradient reflects a cognitive bias towards similarity-based structure in morphology, mirroring similar notions in general category and concept formation. Altogether, we provide further evidence for a more nuanced view of the natural-unnatural distinction in morphology—conceptualised as a gradient rather than a dichotomous property—and suggest a causal link between a general cognitive bias and the ease in which paradigms are transmitted, both in language change and in laboratory settings.
Our findings furthermore contribute to the literature on the syntagmatic (Crysmann & Bonami 2016) and paradigmatic (Corbett 2015; Stump 2001) architecture of grammar. These two dimensions have mostly been treated separately. Here, however, we learn that the positional properties of markers appear to be subject to very similar cross-linguistic probabilities and cognitive biases as other more characteristically paradigmatic phenomena like syncretism (Saldana et al. 2022). We contribute as well to the typological literature by further clarifying the possible types of positional splits, and by providing a large cross-linguistic sample of them. Within the experimental literature, our findings provide evidence for the cognitive relevance of (a gradient notion of) naturalness in a novel domain, and the generality of the proposed similarity-based structure bias in morphological learning.
The combined use of typological and experimental approaches (and their striking agreement in this particular case) constitutes an ideal outcome for the progress of the discipline. A similar agreement of learning complexity and cross-linguistic probability has been found in the domain of phonological features and contrasts Pater & Moreton (2012); Moreton & Pater (2012); Moreton et al. (2017). Future research could be profitably aimed at exploring the generality of this bias further, by checking its applicability to other traits—for example, deeply morphological ones such as the predictive structures within paradigms (see Ackerman & Malouf 2016). The phenomenon can be explored not only in more breadth, but also in more depth, for example by confirming whether there are indeed exponential, not linear, gains of naturalness, and why this might be so. These and related avenues of research will be left for the future.
Data accessibility statement
All experimental materials, data and data analysis reported here are available at osf.io/hy76j/, and the preregistered design and analysis plan is accessible at osf.io/yzcxp.
Notes
- This means that individual markers provide both person and number information in a single indivisible morpheme. The suffix -mi in Fula, for example, indicates first person and singular number. [^]
- As section 3.2.1 will explain, languages tend to encode S identically to either A or P. We will not count markers twice just because they index more than one role. [^]
- We only have 28 languages containing du and thus 3×3 paradigms. The surveyed data for these paradigms can be found in the supplementary materials in osf.io/hy76j/. [^]
- Note that we here give a presuppositional semantics to features (Cooper 1983; Heim & Kratzer 1998; Heim 2008). Also note that in this study we focus on verbal agreement paradigms, that is, on paradigms of agreement targets, for which we assume the semantics of the controllers they agree with. [^]
- An even more unnatural pattern would have no cells sharing values with any other cells (e.g., 1pl, 2sg, 3du). Three-cell patterns of this kind rely on the existence of a third number value (e.g., ‘dual’ or ‘paucal’) which is cross-linguistically less common and are hence beyond our purview in this section. This most unnatural type (XX) will appear, however, in the experimental section 4. [^]
- There are six pairs of cells among these: 1sg/2sg, 2sg/2pl, 2pl/3pl, 1sg/2pl, 1sg/2pl, and 2sg/3pl, the first three of which share half (50%) of their values (number, person, and number respectively) and the last 3 of which share no values (0%). The average is, hence, 25%. [^]
- Notice how neither of the person values over which the latter pattern spreads (1 and 2) appears in any other cells, while the values 1 and 2 occur in cells both inside and outside the L pattern. [^]
- As advanced in the previous section (see Table 4), we do count multiple paradigms in the same language when different TAM, inflection class, polarity, or voice values are associated with differences in the placement of person-number agreement markers. Hence, we include as many different paradigms as different positional splits exist in the language, regardless of whether these paradigms are A or P, present or past, active or passive, etc. We control for the relatedness of paradigms within the same language family in our statistical model. [^]
- Note that 1/4th of these will be instantiated by zero, which we disregarded from the cross-linguistic language data on ontological grounds. The number of logically possible non-zero Ns in this paradigm is thus only 162 (0.04 on average per paradigm). This is the comparative baseline against which we can assess the over-/under-representation of the cross-linguistic data. [^]
- Patterns with 0% similarity refer to 2-cell X patterns, those with 17% to 3-cell X patterns and those with 25%, to 4-cell X patterns. Both 3-cell L patterns and N/L 4-cell patterns have 33% similarity scores and both 3-cell N patterns and 2-cell N/L patterns 50%. [^]
- Following the discussion with one of our reviewers, we furthermore fitted the same model with similarity scores based on an alternative binary minimal feature structure with the features of [±speaker], [±participant] and [±singular]. With this feature structure, there are even more bins of different similarity scores (i.e., 0%, 33%, 38%, 44%, 49%, 55% and 66%) and our data becomes too sparse to make reliable inferences about each of the types. However, a general tendency exists whereby most patterns with higher similarity scores (44%, 55% and 66%) tend to be more likely than predicted by chance, while this is not the case for patterns with lower similarity scores, which are suggested to be either less or equally likely than what would be predicted by chance. Results can be seen in the analysis script available at osf.io/hy76j/. [^]
- Although we decided to exclude ∅-based patterns in section 3.2.1 due to the analytic challenge zero-morphs pose in natural languages, we did not consider that they would negatively impact our experiments because all pattern types appear redundantly within the same paradigm. Thus, under the L-type condition for example (see below), a paradigm will have a prefixal and a suffixal 3-cell L patterns, and never just a ∅-based one. [^]
- A summary of (included and excluded) participants’ performance in vocabulary tests can be found in the analysis script at osf.io/hy76j/. [^]
- After the completion of the experiment, participants are also asked to translate English phrases into the artificial language (one for each person-number combination). We include this translation survey to further monitor participant’s vocabulary attainment during learning. A summary of the results from these translation surveys can be found in the analysis script at osf.io/hy76j/. [^]
- Note that in our pre-registration (available at osf.io/yzcxp) we specified the reverse order for the levels in Condition because we assumed that the difference between the no-split and the natural conditions would be very small; however, the data suggests that the difference is actually quite large and renders the original order of the levels in the pre-registered model inadequate. Comparing any level to an average containing the no-split condition will exaggerate any difference in learnability and wrongly suggest very strong evidence for any difference between the levels. We nevertheless provide the results from the model with the pre-registered order of levels in the analysis script available at osf.io/hy76j/. [^]
- The model’s diagnostics are available at osf.io/hy76j/. [^]
- Although other approaches to naturalness (e.g., Natural Morphology: Dressler 1999; Andersen 2008) have also conceived of it as a scale, the scale on those accounts is not defined in terms of the semantic space alone but integrates a variety of measures, including markedness, frequency, simplicity, and observed synchronic and diachronic preference for a category or structure. [^]
- In 3×2 paradigms with L patterns, number is structurally consistent in two out of three persons, which might make L more learnable. This does not hold in 3×2 paradigms with X patterns, nor in 3×3 paradigms in either condition. In these, positional differences are found inside every person and number value. [^]
Ethics and consent
The study was approved the Ethics Committee of the School of Philosophy at the University of Zurich (Authorisation Nr. 21.9.15). Research practices follow the Ethical Guidelines for Psychologists of the Swiss Society for Psychology (SGP) and the Ethical Principles of Psychologists and Code of Conduct of the American Psychological Association (APA).
Funding information
This research has been partially funded by the NCCR Evolving Language, Swiss National Science Foundation (Agreement Nr. 51NF40_180888).
Acknowledgements
We would like to thank the developers of the open-source softwares used for this study: Josh de Leeuw and collaborators for the development of jsPsych De Leeuw (2015), and Vanessa Sochat for the curation of The Experiment Factory (Sochat 2018). We also would like to thank the comments and feedback of three anonymous reviewers of Glossa, who have helped improve this paper.
Competing interests
The authors have no competing interests to declare.
Author contributions
Conceptualisation, Methodology: BB, BH, CS. Investigation, Resources, Writing - Original Draft, Software, Validation, Formal analysis, Data Curation: BH, CS. Writing - Review & Editing: BB, BH, CS, JM.
References
Aalberse, Suzanne Pauline. 2007. The typology of syncretisms and the status of feature structure. verbal paradigms across 355 Dutch dialects. Morphology 17(1). 109–149. DOI: http://doi.org/10.1007/s11525-007-9111-0
Ackerman, Farrell & Malouf, Robert. 2013. Morphological organization: The low conditional entropy conjecture. Language, 429–464. DOI: http://doi.org/10.1353/lan.2013.0054
Ackerman, Farrell & Malouf, Robert. 2016. Implicative relations in word-based morphological systems. In Hippisley, Andrew & Stump, Gregory (eds.), The Cambridge handbook of morphology, 297–328. Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/9781139814720.012
Andersen, Henning. 2008. Naturalness and markedness. In Willems, Klaas & De Cuypere, Ludovic (eds.), Naturalness and iconicity in language, 101–119. Amsterdam: John Benjamins. DOI: http://doi.org/10.1075/ill.7.07and
Arnott, David W. 1970. The nominal and verbal system of Fula. Leeds: Clarendon Press.
Aronoff, Mark. 1994. Morphology by itself: Stems and inflectional classes. Cambridge, MA: MIT Press.
Aronoff, Mark & Xu, Zheng. 2010. A realization optimality-theoretic approach to affix order. Morphology 20(2). 381–411. DOI: http://doi.org/10.1007/s11525-010-9181-2
Baerman, Matthew & Brown, Dunstan & Corbett, Greville G. 2005. The syntax-morphology interface: A study of syncretism, vol. 109. Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/CBO9780511486234
Bickel, Balthasar. 1994. In the vestibule of meaning: Transitivity inversion as a morphological phenomenon. Studies in Language 19. 73–127. DOI: http://doi.org/10.1075/sl.19.1.04bic
Bickel, Balthasar. 2007. Typology in the 21st century: Major current developments. Linguistic Typology. DOI: http://doi.org/10.1515/LINGTY.2007.018
Bickel, Balthasar. 2015. Distributional typology: Statistical inquiries into the dynamics of linguistic diversity. In Heine, Bernd & Narrog, Heiko (eds.), The Oxford Handbook of Linguistic analysis, 2nd edition, 901–923. Oxford University Press. DOI: http://doi.org/10.1093/oxfordhb/9780199677078.013.0046
Bickel, Balthasar & Banjade, Goma & Gaenszle, Martin & Lieven, Elena & Paudyal, Netra Prasad & Rai, Ichchha Purna & Rai, Manoj & Rai, Novel Kishore & Stoll, Sabine. 2007. Free prefix ordering in Chintang. Language, 43–73. DOI: http://doi.org/10.1353/lan.2007.0002
Bickel, Balthasar & Nichols, Johanna. 2013. Inflectional synthesis of the verb. In Dryer, Matthew S. & Haspelmath, Martin (eds.), The world atlas of language structures online, Leipzig: Max Planck Institute for Evolutionary Anthropology. https://wals.info/chapter/22.
Bickel, Balthasar & Nichols, Johanna & Zakharko, Taras & Witzlack-Makarevich, Alena & Hildebrandt, Kristine & Rießler, Michael & Bierkandt, Lennart & Zúñiga, Fernando & Lowe, John B. 2017. The AUTOTYP typological databases. Version 0.1. 0. Online: https://github.com/autotyp/autotyp-data/tree/0.1.0.
Bickel, Balthasar & Witzlack-Makarevich, Alena & Zakharko, Taras & Iemmolo, Giorgio. 2015. Exploring diachronic universals of agreement: Alignment patterns and zero marking across person categories. Agreement from a diachronic perspective 2952. 29–51. DOI: http://doi.org/10.1515/9783110399967-003
Bierwisch, Manfred. 1967. Syntactic features in morphology: General problems of socalled pronominal inflection in German. In To Honour Roman Jakobson: Essays on the occasion of his seventieth birthday, 239–270. De Gruyter Mouton. DOI: http://doi.org/10.1515/9783111604763-022
Blevins, James P. 1995. Syncretism and paradigmatic opposition. Linguistics and Philosophy 18(2). 113–152. DOI: http://doi.org/10.1007/BF00985214
Blevins, James P. forthcoming. Two frameworks of morphological analysis. Linguistic Analysis https://www.academia.edu/42103967/Two_frameworks_of_morphological_analysis.
Blythe, Richard A & Croft, William. 2021. How individuals change language. Plos one 16(6). e0252582. DOI: http://doi.org/10.1371/journal.pone.0252582
Bobaljik, Jonathan David & Sauerland, Uli. 2018. ABA and the combinatorics of morphological features. Glossa: a journal of general linguistics 3(1). DOI: http://doi.org/10.5334/gjgl.345
Bruner, Jerome Seymour & Goodnow, Jacqueline J & Austin, George A. 1956. A study of thinking. John Wiley and sons, Incorporated.
Bürkner, Paul-Christian. 2018. Advanced Bayesian multilevel modeling with the R package brms. The R Journal 10(1). 395–411. DOI: http://doi.org/10.32614/RJ-2018-017
Caballero, Gabriela. 2010. Scope, phonology and morphology in an agglutinating language: Choguita Rarámuri (Tarahumara) variable suffix ordering. Morphology 20(1). 165–204. DOI: http://doi.org/10.1007/s11525-010-9147-4
Caballero, Gabriela & Harris, Alice C. 2012. A working typology of multiple exponence. In Kiefer, Ferenc & Ladányi, Mária & Siptár, Péter (eds.), Current issues in morphological theory: (ir)regularity, analogy and frequency. selected papers from the 14th international morphology meeting, budapest, 13-16 may 2010, 163–188. Amsterdam: John Benjamins Amsterdam. DOI: http://doi.org/10.1075/cilt.322.08cab
Campbell, Amy. 2012. The morphosyntax of discontinuous exponence: University of California, Berkeley dissertation.
Carpenter, Bob & Gelman, Andrew & Hoffman, Matthew D & Lee, Daniel & Goodrich, Ben & Betancourt, Michael & Brubaker, Marcus & Guo, Jiqiang & Li, Peter & Riddell, Allen. 2017. Stan: A probabilistic programming language. Journal of statistical software 76(1). DOI: http://doi.org/10.18637/jss.v076.i01
Carr, Jon W & Smith, Kenny & Culbertson, Jennifer & Kirby, Simon. 2020. Simplicity and informativeness in semantic category systems. Cognition 202. 104289. DOI: http://doi.org/10.1016/j.cognition.2020.104289
Carroll, Matthew J. 2022. Verbose exponence: Integrating the typologies of multiple and distributed exponence. Morphology 32(1). 1–24. DOI: http://doi.org/10.1007/s11525-021-09384-8
Cooper, Robin. 1983. Quantification and syntactic theory, vol. 21. Springer. DOI: http://doi.org/10.1007/978-94-015-6932-3
Corbett, Greville G. 2015. Morphosyntactic complexity: A typology of lexical splits. Language 91(1). 145–193. DOI: http://doi.org/10.1353/lan.2015.0003
Crysmann, Berthold & Bonami, Olivier. 2016. Variable morphotactics in informationbased morphology. Journal of Linguistics 52(2). 311–374. DOI: http://doi.org/10.1017/S0022226715000018
Culbertson, Jennifer & Kirby, Simon. 2016. Simplicity and specificity in language: Domain-general biases have domain-specific effects. Frontiers in psychology 6. 1964. DOI: http://doi.org/10.3389/fpsyg.2015.01964
Culbertson, Jennifer & Smolensky, Paul & Legendre, Géraldine. 2012. Learning biases predict a word order universal. Cognition 122(3). 306–329. DOI: http://doi.org/10.1016/j.cognition.2011.10.017
Cutler, Anne & Hawkins, John A & Gilligan, Gary. 1985. The suffixing preference: A processing explanation. Linguistics 23(5). 723–758. DOI: http://doi.org/10.1515/ling.1985.23.5.723
Cysouw, Michael. 2003. The paradigmatic structure of person marking. Oxford University Press.
Danielsen, Swintha. 2007. Baure: an Arawak language of Bolivia: Radboud University Nijmegen dissertation.
Dautriche, Isabelle & Chemla, Emmanuel & Christophe, Anne. 2016. Word learning: Homophony and the distribution of learning exemplars. Language Learning and Development 12(3). 231–251. DOI: http://doi.org/10.1080/15475441.2015.1127163
De Leeuw, Joshua R. 2015. jsPsych: A JavaScript library for creating behavioral experiments in a Web browser. Behavior research methods 47(1). 1–12. DOI: http://doi.org/10.3758/s13428-014-0458-y
Dressler, Wolfgang U. 1999. What is natural in Natural Morphology (NM). Prague Linguistic Circle Papers 3. 135–144. DOI: http://doi.org/10.1075/plcp.3.11dre
Dryer, Matthew S & Haspelmath, Martin. 2013. The world atlas of language structures online. Leipzig: Max planck institute for evolutionary anthropology. Online: http://wals.info.
Fedzechkina, Maryia & Jaeger, T Florian & Newport, Elissa L. 2012. Language learners restructure their input to facilitate efficient communication. Proceedings of the National Academy of Sciences 109(44). 17897–17902. DOI: http://doi.org/10.1073/pnas.1215776109
Good, Jeff. 2015. Paradigmatic complexity in pidgins and creoles. Word Structure 8(2). 184–227. DOI: http://doi.org/10.3366/word.2015.0081
Good, Jeff. 2016. The linguistic typology of templates. Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/CBO9781139057479
Goodman, Noah D & Tenenbaum, Joshua B & Feldman, Jacob & Griffiths, Thomas L. 2008. A rational analysis of rule-based concept learning. Cognitive science 32(1). 108–154. DOI: http://doi.org/10.1080/03640210701802071
Gottwald, Richard. 1971. Effects of response labels in concept attainment. Journal of Experimental Psychology 91(1). 30. DOI: http://doi.org/10.1037/h0031857
Greenberg, Joseph H. 1966. Synchronic and diachronic universals in phonology. Language 42(2). 508–517. DOI: http://doi.org/10.2307/411706
Harbour, Daniel. 2016. Impossible persons, vol. 74. MIT Press. DOI: http://doi.org/10.7551/mitpress/9780262034739.001.0001
Harley, Heidi & Ritter, Elizabeth. 2002. Person and number in pronouns: A featuregeometric analysis. Language 78(3). 482–526. DOI: http://doi.org/10.1353/lan.2002.0158
Harris, Alice C. 2017. Multiple exponence. Oxford University Press. DOI: http://doi.org/10.1093/acprof:oso/9780190464356.001.0001
Heim, Irene. 2008. Features on bound pronouns. In Adger, D. & Bejar, S. & Harbour, D. (eds.), Phi theory: Phi-features across modules and interfaces, 35–56. Oxford University Press.
Heim, Irene & Kratzer, Angelika. 1998. Semantics in generative grammar. Blackwell Oxford.
Herce, B. 2020. On morphemes and morphomes: Exploring the distinction. Word Structure 13(1). DOI: http://doi.org/10.3366/word.2020.0159
Herce, Borja. 2023. The typological diversity of morphomes: A cross-linguistic study of unnatural morphology. Oxford University Press. DOI: http://doi.org/10.1093/oso/9780192864598.001.0001
Hualde, José Ignacio & De Urbina, Jon Ortiz. 2011. A grammar of Basque, vol. 26. Walter de Gruyter. DOI: http://doi.org/10.1515/9783110895285
Hyman, Larry M. 2003. Suffix ordering in Bantu: A morphocentric approach. In Yearbook of morphology 2002, 245–281. Amsterdam: Springer. DOI: http://doi.org/10.1007/0-306-48223-1_8
Inkelas, Sharon. 1993. Nimboran position class morphology. Natural Language & Linguistic Theory 11(4). 559–624. DOI: http://doi.org/10.1007/BF00993014
Kimball, Geoffrey David. 1985. A descriptive grammar of Koasati (louisiana): Tulane University dissertation.
Kirby, Simon & Smith, Kenny & Brighton, Henry. 2004. From UG to universals: Linguistic adaptation through iterated learning. Studies in Language. International Journal sponsored by the Foundation “Foundations of Language” 28(3). 587–607. DOI: http://doi.org/10.1075/sl.28.3.09kir
Kurz, Solomon. 2019. Robust linear regression with Student’s t distribution. https://solomonkurz.netlify.app/post/robust-linear-regression-with-the-robuststudent-s-t-distribution/.
Landau, Barbara & Shipley, Elizabeth. 2001. Labelling patterns and object naming. Developmental science 4(1). 109–118. DOI: http://doi.org/10.1111/1467-7687.00155
Luís, AR & Bermúdez-Otero, R. 2016. The morphome debate. Oxford: Oxford University Press. DOI: http://doi.org/10.1093/acprof:oso/9780198702108.001.0001
Maiden, Martin. 2018. The Romance verb: Morphomic structure and diachrony. Oxford: Oxford University Press. DOI: http://doi.org/10.1093/oso/9780199660216.001.0001
Maldonado, Mora & Culbertson, Jennifer. 2022. Person of interest: Experimental investigations into the learnability of person systems. Linguistic Inquiry 53(2). 295–336. DOI: http://doi.org/10.1162/ling_a_00406
Maldonado, Mora & Saldana, Carmen & Culbertson, Jennifer. 2020. Learning biases in person-number linearization. In Proceedings of the 50th Annual Meeting of the North East Linguistic Society 2. 163–176. Amherst, MA: University of Massachusetts GLSA. DOI: http://doi.org/10.31234/osf.io/5s2r8
Mansfield, John & Saldana, Carmen & Hurst, Peter & Nordlinger, Rachel & Stoll, Sabine & Bickel, Balthasar & Perfors, Andrew. 2022. Category clustering and morphological learning. Cognitive Science 46(2). e13107. DOI: http://doi.org/10.1111/cogs.13107
Mansfield, John & Stoll, Sabine & Bickel, Balthasar. 2020. Category clustering: A probabilistic bias in the morphology of verbal agreement marking. Language 96(2). 255–293. DOI: http://doi.org/10.1353/lan.2020.0021
McCarthy, John & Prince, Alan. 1990. Prosodic morphology and templatic morphology. University of Massachusetts Occasional Papers in Linguistics 16(2). DOI: http://doi.org/10.1075/cilt.72.05mcc
McCarthy, John J. 1981. A prosodic theory of nonconcatenative morphology. Linguistic inquiry 12(3). 373–418.
McElreath, Richard. 2016. Statistical rethinking: A Bayesian course with examples in R and Stan. CRC press. DOI: http://doi.org/10.1201/9781315372495
Mielke, Jeff. 2004. The emergence of distinctive features. Oxford: Oxford University Press.
Miller, Wick R. 1965. Acoma grammar and texts. Berkeley: Univ. of California Press.
Moreton, Elliott & Pater, Joe. 2012. Structure and substance in artificial-phonology learning, part i: Structure. Language and linguistics compass 6(11). 686–701. DOI: http://doi.org/10.1002/lnc3.363
Moreton, Elliott & Pater, Joe & Pertsova, Katya. 2017. Phonological concept learning. Cognitive science 41(1). 4–69. DOI: http://doi.org/10.1111/cogs.12319
Muysken, PC. 1986. Approaches to affix order. Linguistics 24. 629–643. DOI: http://doi.org/10.1515/ling.1986.24.3.629
Neisser, Ulric & Weene, Paul. 1962. Hierarchies in concept attainment. Journal of Experimental Psychology 64(6). 640. DOI: http://doi.org/10.1037/h0042549
Nevins, Andrew. 2015. Productivity and portuguese morphology: How experiments enable hypothesis-testing. In Aboh, EO & Schaeffer, JC & Sleeman, P (eds.), Romance languages and linguistic theory, 175–201. John Benjamins. DOI: http://doi.org/10.1075/rllt.8.10nev
Nevins, Andrew & Rodrigues, Cilene & Tang, Kevin. 2015. The rise and fall of the lshaped morphome: diachronic and experimental studies. Probus 27(1). 101–155. DOI: http://doi.org/10.1515/probus-2015-0002
Noyer, Robert Rolf. 1992. Features, positions and affixes in autonomous morphological structure: MIT dissertation.
Pater, Joe & Moreton, Elliott. 2012. Structurally biased phonology: complexity in learning and typology. Journal of the English and Foreign Languages University 3(2). 1–44.
Pertsova, Katya. 2007. Learning form-meaning mappings in the presence of homonymy: University of California Los Angeles dissertation.
Pertsova, Katya. 2014. Logical complexity in morphological learning: effects of structure and null/overt affixation on learning paradigms. In Annual meeting of the Berkeley linguistics society 38. 401–413. DOI: http://doi.org/10.3765/bls.v38i0.3343
Pothos, Emmanuel M & Chater, Nick & Stewart, Andrew J. 2004. Information about the logical structure of a category affects generalization. British Journal of Psychology 95(3). 371–386. DOI: http://doi.org/10.1348/0007126041528158
Reali, Florencia & Griffiths, Thomas L. 2009. The evolution of frequency distributions: Relating regularization to inductive biases through iterated learning. Cognition 111(3). 317–328. DOI: http://doi.org/10.1016/j.cognition.2009.02.012
Rice, Keren. 2000. Morpheme order and semantic scope: Word formation in the Athapaskan verb, vol. 90. Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/CBO9780511663659
Rice, Keren. 2011. Principles of affix ordering: An overview. Word Structure 4(2). 169–200. DOI: http://doi.org/10.3366/word.2011.0009
Roberts, John R & Roberts, John T. 1987. Amele. Milton Park, UK: Routledge.
Round, Erich R. 2021. GlottoTrees: Phylogenetic trees in linguistics. https://github.com/erichround/glottoTrees. R package version 0.1.
Round, Erich R & Corbett, Greville G. 2017. The theory of feature systems: One feature versus two for kayardild tense-aspect-mood. Morphology 27(1). 21–75. DOI: http://doi.org/10.1007/s11525-016-9294-3
Saeed, John. 1999. Somali, vol. 10. Amsterdam: John Benjamins. DOI: http://doi.org/10.1075/loall.10
Saldana, Carmen & Herce, Borja & Bickel, Balthasar. 2022. More or less unnatural: Semantic similarity shapes the learning and cross-linguistic distributions of morphological paradigms. Open Mind: Discoveries in Cognitive Science. DOI: http://doi.org/10.1162/opmi_a_00062
Saldana, Carmen & Kirby, Simon & Truswell, Robert & Smith, Kenny. 2019. Compositional hierarchical structure evolves through cultural transmission: an experimental study. Journal of Language Evolution 4(2). 83–107. DOI: http://doi.org/10.1093/jole/lzz002
Saldana, Carmen & Oseki, Yohei & Culbertson, Jennifer. 2021a. Cross-linguistic patterns of morpheme order reflect cognitive biases: An experimental study of case and number morphology. Journal of Memory and Language 118. 104204. DOI: http://doi.org/10.1016/j.jml.2020.104204
Saldana, Carmen & Smith, Kenny & Kirby, Simon & Culbertson, Jennifer. 2021b. Is regularization uniform across linguistic levels? Comparing learning and production of unconditioned probabilistic variation in morphology and word order. Language Learning and Development 17(2). 158–188. DOI: http://doi.org/10.1080/15475441.2021.1876697
Schlenker, Philippe. 2003. Indexicality, logophoricity, and plural pronouns. In Lecarme, Jacqueline (ed.), Research in afroasiatic grammar ii. 409–428. John Benjamins. DOI: http://doi.org/10.1075/cilt.241.19sch
Seiler, Walter. 1985. Imonda, a Papuan language. The Australian National University.
Seržant, Ilja A & Moroz, George. 2022. Universal attractors in language evolution provide evidence for the kinds of efficiency pressures involved. Humanities and Social Sciences Communications 9(1). 1–9. DOI: http://doi.org/10.1057/s41599-022-01072-0
Shepard, Roger N & Hovland, Carl I & Jenkins, Herbert M. 1961. Learning and memorization of classifications. Psychological monographs: General and applied 75(13). 1. DOI: http://doi.org/10.1037/h0093825
Shlonsky, Ur. 1989. The hierarchical representation of subject verb agreement. Unpublished manuscript.
Silvey, Catriona & Kirby, Simon & Smith, Kenny. 2019. Communication increases category structure and alignment only when combined with cultural transmission. Journal of Memory and Language 109. 104051. DOI: http://doi.org/10.1016/j.jml.2019.104051
Smith, Kenny. 2018. The cognitive prerequisites for language: insights from iterated learning. Current opinion in behavioral sciences 21. 154–160. DOI: http://doi.org/10.1016/j.cobeha.2018.05.003
Smith, Kenny & Kirby, Simon & Brighton, Henry. 2003. Iterated learning: A framework for the emergence of language. Artificial life 9(4). 371–386. DOI: http://doi.org/10.1162/106454603322694825
Sochat, Vanessa. 2018. The experiment factory: Reproducible experiment containers. Journal of Open Source Software 3(22). 521. DOI: http://doi.org/10.21105/joss.00521
Song, Hanbyul & White, James. 2022. Interaction of phonological biases and frequency in learning a probabilistic language pattern. Cognition 226. 105170. DOI: http://doi.org/10.1016/j.cognition.2022.105170
Spencer, Andrew. 2003. Putting some order into morphology: Reflections on Rice (2000) and Stump (2001). Journal of Linguistics 39(3). 621–646. DOI: http://doi.org/10.1017/S0022226703002123
Stump, Gregory T. 1997. Template morphology and inflectional morphology. In Yearbook of morphology 1996, 217–241. Amsterdam: Springer. DOI: http://doi.org/10.1007/978-94-017-3718-0_12
Stump, Gregory T. 2001. Inflectional morphology: A theory of paradigm structure, vol. 93. Cambridge: Cambridge University Press. DOI: http://doi.org/10.1017/CBO9780511486333
Terraza, Jimena. 2009. Grammaire du Wichi: phonologie et morphosyntaxe: Université du Québec à Montréal dissertation.
Trommer, Jochen. 2003. The interaction of morphology and syntax in affix order. In Yearbook of morphology 2002, 283–324. Amsterdam: Springer. DOI: http://doi.org/10.1007/0-306-48223-1_9
Trott, Sean & Bergen, Benjamin. 2022. Languages are efficient, but for whom? Cognition 225. 105094. DOI: http://doi.org/10.1016/j.cognition.2022.105094
Völlmin, Sascha. 2017. Towards a grammar of Gumer - phonology and morphology of a Western Gurage variety: University of Zurich dissertation.
Watkins, Calvert & Mayrhofer, Manfred & Kuryowicz, Jerzy. 1969. Geschichte der indogermanischen Verbalflexion. Carl Winter.
Wyngaerd, Guido Vanden. 2018. The feature structure of pronouns: A probe into multidimensional paradigms. In Baunaz, Lena & Haegeman, Liliane & De Clercq, Karen & Lander, Eric (eds.), Exploring Nanosyntax, Oxford: Oxford University Press. DOI: http://doi.org/10.1093/oso/9780190876746.003.0011
Xu, Fei & Tenenbaum, Joshua B. 2007. Word learning as bayesian inference. Psychological review 114(2). 245. DOI: http://doi.org/10.1037/0033-295X.114.2.245