1 Introduction
This paper addresses the relationship between the strength of phonotactic constraints and the way in which multiple coincident violations of such constraints interact in the grammar. Some grammatical approaches predict that violations simply stack up to yield a penalty that is the sum of the component penalties. Other approaches predict that forms with multiple violations are better or worse than would be obtained by adding the individual penalties, and indeed, cases of this sort have been observed in lexical counts and experimental results. As we will demonstrate, in some grammatical approaches, the predicted size of the penalty varies depending on the strength of the restrictions involved. We investigate whether there is a causal relationship between the strength of a given phonotactic restriction and how it combines with other restrictions in the grammar. Using an Artificial Grammar Learning (AGL) paradigm, we find that as we decrease the strength of phonotactic restrictions by introducing exceptions, we observe an increasing penalty for multiple violations beyond the simple combination of the independent penalties. That is, participants’ acceptability ratings for doubly-marked forms are lower than what is obtained by adding up the independent penalties in acceptability for each of those forms’ individual violations. We argue that this supports a grammatical model in which the degree of penalty assigned to multiple constraint violations is a deterministic function of the weights of the constraints involved. We discuss the implications of this model for theories of phonotactics, and the contents of the constraint set.
2 Computing grammaticality across multiple marked structures
2.1 Linear, super-linear, and sub-linear cumulativity
We begin by laying out some terminology in order to state our hypothesis as precisely as possible. The broad domain of inquiry is about the acceptability of words that contain multiple marked structures. This contains an empirical question (how does the acceptability of multiply marked words relate to that of singly marked words), and a theoretical question (how do grammatical models combine violations to compute an overall grammaticality).
Empirically, the question is how decomposable acceptability judgments of strings are into separate components. A natural default assumption is that if a word has two dispreferred substrings (i.e., two Markedness violations), each contributes its own penalty independently, so the doubly-marked form is exactly as unacceptable or improbable as one would expect based on its individual violations. There are various ways of computing such an expectation. In this section, we focus on expectations implemented in terms of probability, because several current grammatical formalisms generate probability distributions over outputs. Assuming that a model is able to predict the probability of a form with a single Markedness violation, then a word with two Markedness violations would have a probability equal to the joint probability of the two Markedness violations. The joint probability of two violations is equal to the product of the independent probabilities of those violations, or, in log-space, their sum. We use the term linear to refer to the situation where the Markedness violations of a string all affect the outcome independently. The assumption of linear interactions is seen, for example, in how the “Expected” values in Observed/Expected counts are typically calculated (Frisch et al. 2004; Wilson & Obdeyn 2009), and also in how n-gram models combine probabilities of each successive n-gram (Jurafsky & Martin 2009: chapter 4). Weighted constraint models such as Harmonic Grammar (Legendre et al. 1990) and MaxEnt (Smolensky 1986; Goldwater & Johnson 2003) also calculate the Harmony of a candidate as the linear sum of its weighted violations. However, this alone does not guarantee that we will observe linear interactions empirically, since the way that the acceptability or probability of a form is determined from its Harmony in these frameworks may make the actual acceptability or probability of a doubly-marked form higher or lower than the joint probability of its parts (more on this below).
With this definition of linearity in hand, it is now straightforward to define deviations from linearity. Specifically, if the probability or acceptability of a multiply-marked form is lower than expected based on the independent probability or acceptability of its parts, we follow Smith & Pater (2020) in calling this a super-linear interaction.1 Similarly, we can say that if the probability or acceptability of a multiply-marked form is higher than expected, it is a sub-linear interaction.
On the theoretical side, linearity can also be a property of grammatical models. Here, it refers to how models combine different theoretical quantities to yield an overall grammaticality value. For example, as noted above, a model that adds weighted Markedness violations to yield a Harmony value is linear, in the sense that Harmony is decomposable into the component violations. For present purposes, we are not directly concerned with whether a given grammatical model is a linear model, though in practice, all of the models that we consider are. Rather, we are concerned with what models predict for the candidates’ grammaticality-determined probability, as observed through acceptability judgments.
2.2 Evidence for cumulativity of violations
A growing body of evidence in the phonological literature supports the view that Markedness violations are cumulative: when speakers judge the well-formedness of a word, their judgement is not based on only the most marked structure it contains (as predicted by strict-ranking constraint-based models such as Optimality Theory (Prince & Smolensky 1993) and its variants). Rather, speakers attend to all relevant structures in a domain, and weight their importance according to their severity (as predicted by weighted-constraint models such as Harmonic Grammar (Legendre et al. 1990) and its variants). This aggregation of evidence across different structures was termed cumulativity by Jäger & Rosenbach (2006),2 and is observed both in the probability of a given structure in the lexicon, and that of experimentally-determined acceptability.
Recent work has focused on how exactly the contributions to markedness from each of a number of structures are combined in the grammar. Specifically, there are some indications that the total markedness of a word containing multiple marked structures might not be accurately measured by the simple combination of the markedness of its parts. In lexical attestation, nonce word judgments, and phonological patterning it’s been observed that sometimes, strings with two marked structures are penalized to a greater extent than obtained by adding up the markedness of each of the violations assessed alone — super-linearity. An example of this type of cumulativity can be found in the lexicon of English: as part of a study of English monosyllable phonotactics, Albright (2012) found that 491 (8.2%) of monosyllables in the CELEX database (Baayen et al. 1996) had a stop+l onset, and 47 (3.2%) had a s+stop coda. However, the number of #stop+l…s+stop# words was lower than either of these, with only 7 occurrences (0.11%). This instance the cumulativity exhibited is super-linear in nature: the combination of independent probabilities of the marked syllable margins alone predicts that 8.2% × 3.2% = 0.22% of the monosyllables in the database — about 16 unique words — should exhibit both the marked onset and marked coda. Similar data in lexical studies have also been noted in Albright (2008), which finds that Lakhota roots which contain multiple structures which are only moderately uncommon, such as consonant clusters and fricatives, co-occur in dramatically fewer roots than predicted by their joint probability. Also in this vein is a study by Yang et al. (2018), who carry out a comparison of English and Mandarin monosyllables and find that the attested monosyllabic lexicons are more well-formed than would be expected by the independent probabilities of their parts.
Although lexical statistics are often advanced as evidence of synchronic phonological knowledge, divergences between lexical statistics and productive grammatical knowledge are well-known (Becker et al. 2011; Hayes & White 2013 among others). Indeed, Frisch (1996); Martin (2007; 2011) and Beguš (2018) highlight how the phonotactic structure of the lexicon can change over time so as to favor well-formed words at the expense of marked forms as part of a self-amplifying feedback cycle with basic properties of the synchronic phonological grammar. Thus simply observing that a generalization holds of a language’s lexicon does not necessarily imply that it enjoys a cognitively real status in the synchronic grammar of its speakers. Therefore it is important to ask whether super-linear cumulativity is exhibited synchronically.
Super-linear cumulativity has also been observed in nonce word judgments, though the data are relatively scarce. Albright (2012) replicated a nonword acceptability judgment task from Bailey & Hahn (2001) which asked subjects to rate the acceptability of novel English monosyllables containing onset clusters (e.g. [krɛn, draf]), coda clusters (e.g. [lɛsk, mısp]), or both (e.g. [drısp, krɛsk]). Albright then modeled whether the acceptability of the doubly-marked forms could be predicted solely on the basis of their constituent violations and found that it could not: doubly-marked forms such as [drısp] were rated less acceptable than predicted by the sum of their independent penalties.
Other cases of super-linearity have been documented in phonological alternations: for example Smith & Pater (2020) note that super-linear behavior is observed in the interaction of deletion and epenthesis in the surface-realization of French schwa. Green & Davis (2014) find that multiple optional syllable structure simplifications in colloquial Bamana are dramatically less likely to co-occur than expected given the product of the probability of each independent simplification process. Kim (2019), building on Kumagai (2017), demonstrates the cumulative effect of nasals on blocking the inter-morpheme obstruent-voicing process rendaku in Japanese compounds which also displays super-linear behavior. Kawahara & Kumagai (2021) re-examine the data on nasals with a better-controlled experiment, and do not replicate Kumagai (2017)’s findings of super-linearity. However, they unexpectedly find that two approximants ([w] or [j]) in the second element of a compounds does exert a blocking effect on Rendaku that is dramatically stronger than that of a single approximant, again a case of super-linear cumulativity. Super-linear cumulativity has also been observed in the contribution of different phonological structures to the likelihood of belonging to a specific lexical class (Shih 2017).
At the same time, not all studies that have examined cumulativity have found it to be super-linear: Breiss (2020) tested for cumulativity in phonotactic markedness using an AGL paradigm, and found that, when trained on a language which conformed to two exceptionless phonotactics, participants judged words that violated both phonotactics as less well-formed than those which violated only one, again demonstrating cumulativity but without evidence of super-linearity. Durvasula & Liter (2020) also used an AGL task to examine multiple concurrent phonological generalizations learned over representations of different grain-sizes, and also found results that are compatible with linear cumulativity. Moving beyond the domain of linguist-created languages, Kawahara & Breiss (2021) examined cumulativity in sound symbolism, and found that participants combined multiple phonological cues to the same sound-symbolic quality in a cumulative manner in the domain of Pokémon names (see also Kawahara & Moore 2021; Kawahara 2021). Pizzo (2015) found that English-speaking participants judged words which violated English syllable-margin phonotactics in one location, ex. plavb, tlag as less acceptable than one which violated none — plag — and crucially more acceptable than those which violated both, ex., tlavb. Importantly, the penalty for doubly-marked forms in her data was not more than the expected value under linear cumulativity (though we return to these findings in more detail in section 6.3).
Summarizing the state of the literature on cumulativity reviewed above, we find that there are conflicting claims about the linearity of cumulative phonological interactions, and further there is a lack of clarity about which factor(s) might lead a given instance of cumulativity to be (non-)linear in the first place, since studies on the topic draw on acceptability judgements from both real and artificial languages, as well as studies of lexical attestation, the distribution of sub-classes of forms within the lexicon, and factors influencing phonological alternations.
2.3 Deriving non-linear cumulativity with grammatical models
Grammatical models differ in whether they predict the existence of linear, super-linear and sub-linear effects. Optimality Theory (OT; Prince & Smolensky (1993)) assumes strict constraint domination, and predicts no super-linear interactions. Categorical OT cannot derive probabilities other than 0 or 1 at all, and if a candidate contains two different intolerable (p = 0) violations, it will be eliminated by the higher ranked violation, with no additional cumulative effect of the lower-ranked violation; that is, only one violation contributes, but this is indistinguishable from the effect of two intolerable violations (probability of 0 is equivalent to probability 0 × probability 0) (see Coetzee 2004 for further discussion of grammaticality in categorical OT). Stochastic OT (Boersma et al. 1997; Boersma & Hayes 2001) can assign gradient probabilities, and Smith & Pater (2020) have shown that doubly-marked candidates may receive a probability that is not identical to the probability of its highest violation, but the interaction is always sub-linear, and never super-linear.
Weighted constraint models, by contrast, do not employ strict domination, and as mentioned above, all of the weighted violations in a form are summed to compute the Harmony of a candidate. Whether or not adding multiple Markedness violations leads to linear or super-linear interactions depends on how acceptability or probability are then determined, based on the Harmony of the candidates. In Harmonic Grammar (Legendre et al. 1990), the candidate with the best Harmony is chosen as the categorical winner, with the consequence that a single intolerable violation is all that matters in eliminating forms, as in categorical Optimality Theory. Noisy Harmonic Grammar assigns probabilities much like Stochastic OT by imposing noise on Harmony values, and the predictions for how this affects probability depends on implementational details of how noise is added (Hayes 2017; Zuraw & Hayes 2017; Flemming 2021). This has the potential to derive not only sub-linear and linear cumulativity, but also super-linear cumulativity under certain circumstances (Smith & Pater 2020 and others).
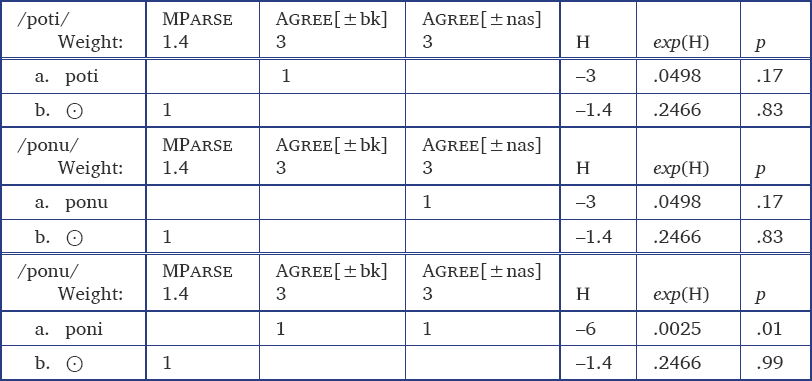
Maximum Entropy (MaxEnt) models (Smolensky 1986; Goldwater & Johnson 2003) have the potential to derive a wider range of non-linear interactions. In MaxEnt models, the probability of a candidate is derived from the Harmony via a non-linear transformation: exp(Harmony) (for details see Jurafsky & Martin 2009: chapter 5). Whether or not this yields super-linear interactions depends on certain assumptions about the candidate set, and how Markedness and Faithfulness constraints interact (Pater 2009b). The tableaux in Table 1 illustrate one way in which the probability of a doubly-marked form may come to be less than the product of the probability of individual violations (super-linearity). In these tableaux, we assume that the fully faithful form competes with a single “Null Parse” candidate, represented as [⊙], which represents the choice not to produce the form (Prince & Smolensky 1993, p. 51; Wolf & McCarthy 2010).3 The Null Parse violates a single constraint, MParse. The Harmony (H) of a candidate is the negated weighted sum of its violations, and the probability is exp(H) divided by the summed exponentiated Harmony for all candidates. The Markedness constraints Agree[±back] and Agree[±nasal] demand that adjacent vowels have the same value for backness, and adjacent consonants have the same value for nasality, respectively. The tableaux show that if MParse is assigned a weight of 5 and the Agree constraints are assigned weights of 3, the probability of the doubly-marked form [poni], which violates both Agree[±back] and Agree[±nasal], is only .27, which is far lower than the product of the probabilities of the independent violations in [poti] and [ponu] (.882 = .78).
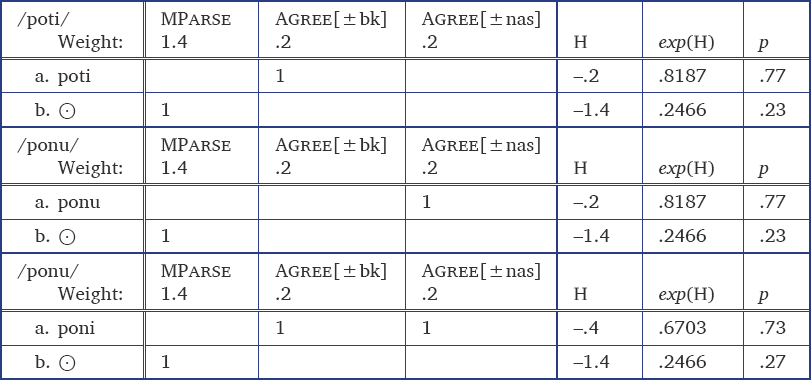
In a MaxEnt model that uses the Null Parse in this way, whether or not a cumulative interaction is expected to be super-linear, linear, or even sub-linear depends on the strengths of the restrictions (cf. Smith & Pater 2020: p. 23). In the example in Table 1, the restrictions against disharmonic forms are, qualitatively speaking, relatively weak, and super-linear cumulativity is predicted. Compare this behavior with the example in Table 2, where the same restrictions are stronger, reflected in the lower weight of MParse relative to the Markedness constraints. Here, we find a less obvious degree of super-linear cumulativity, since the probably assigned to a single violation is already low (.17), and the joint probability of two independent violations (.03) is scarcely different from the predicted probability of a doubly-marked form (.01). Floor effects of this type are not the only circumstance in which this model can predict linear cumulativity, but this example is chosen to resemble the exceptionless phonotactic restrictions in the Breiss (2020) experiment, which failed to detect super-linear cumulativity.
In this framework, it is also possible to derive sub-linear cumulativity under certain weighting conditions. For example, as shown in Table 3, if the weight of MParse is 1.4 and the weights of the Markedness constraints are .2, the predicted probability of a doubly-marked form (.73) is actually greater than the joint probability of two independent violations (.772 = .59). We return to the issue of sub-linear cumulativity in section 6.3.
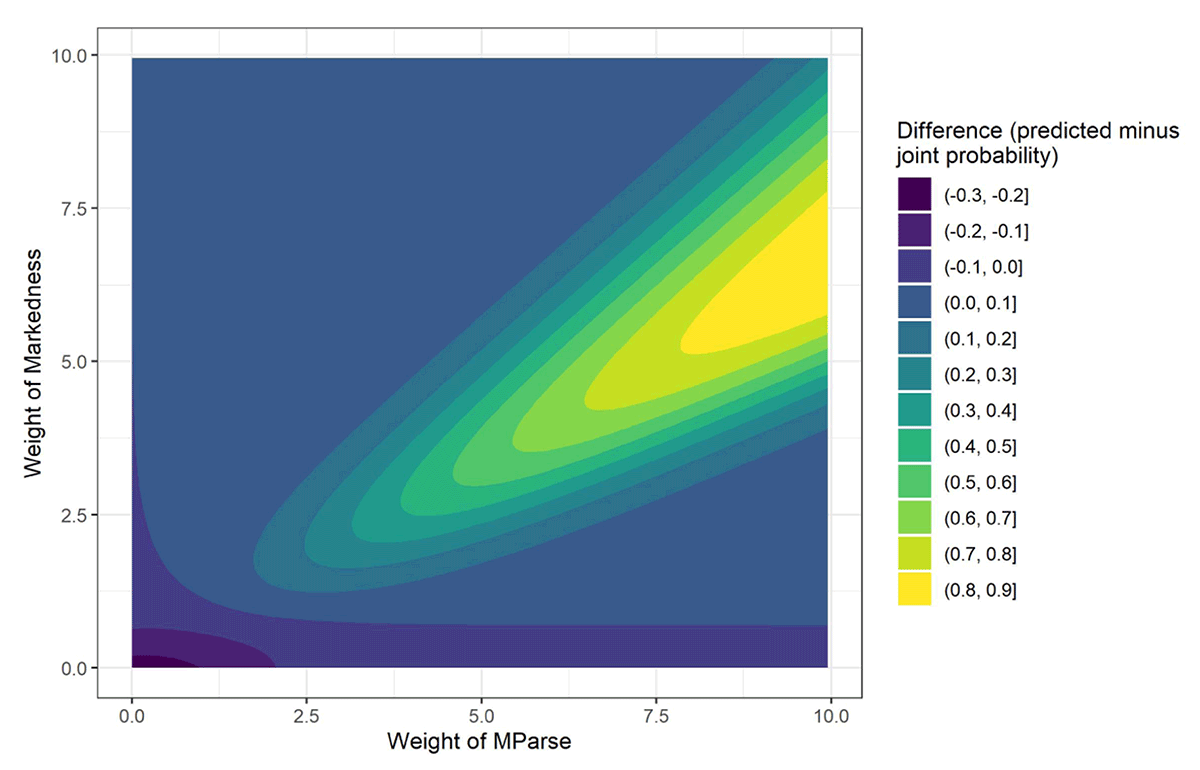
The preceding examples show that the MaxEnt with null-parse approach has the expressive power to capture various types of linear, super-linear, and sub-linear cumulativity. The approach is constrained, however: it is not able to capture any arbitrary interaction, but rather, the degree of (non-)linearity emerges as a by-product of the strength of the restrictions involved, and the absolute value of the constraint weights. The relation between the weight of the constraints and their predicted cumulative interaction is shown in Figure 1, which illustrates how varying the weight of MParse and Markedness constraints determines whether the interaction is super-linear, linear, or sub-linear. A formal description of the specific weighting conditions under which Maximum Entropy grammars with MParse exhibit different types of linearity is provided in the appendix.
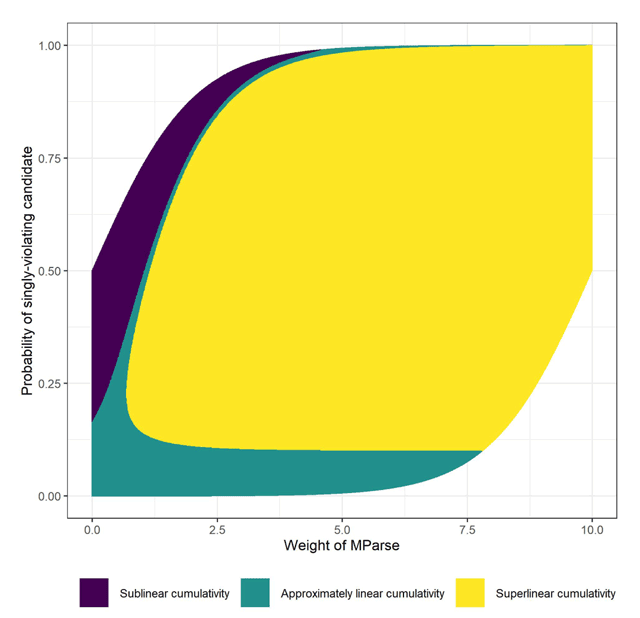
In an experimental manipulation, we cannot vary the weights that learners assign to markedness and MParse directly, but rather, we vary how strongly the markedness restriction is enforced. Figure 2 recasts the relation between MParse and markedness, focusing on how linearity depends on the probability assigned to outputs with a single Markedness violation. A probability of zero reflects a strongly enforced markedness restriction, and a probability of one reflects a completely unenforced restriction.
The goal of this study is to test the prediction that the degree of linearity in the cumulative interaction of two constraints depends on the strength of the restrictions involved. Note that since we do not have any way to derive expectations about the absolute weights of constraints in the learned grammar, we do not make a specific prediction about the amount of non-linearity that should be introduced by a particular manipulation of the strength of a restriction. We do expect that by exposing learners to languages with varying strengths of phonotactic restriction, we should observe different points along a single vertical “slice” of Figure 2, with the concomitant shift between linear and non-linear cumulativity. Furthermore, for a large portion of weight space, the model predicts that as markedness restrictions get weaker (from bottom to top of the plot), their predicted interaction shifts from linear to super-linear.
In what follows, we will first test whether speakers exhibit super-linear cumulativity as phonotactic restrictions get weaker. We then test whether learners infer super-linear cumulativity as a function of the strength of the restrictions, even in the absence of overt evidence. A positive answer to both will support a theoretical device like the MaxEnt model illustrated here, in which super-linear cumulativity is an automatic consequence of the constraint weights. This finding also has the potential to shed light on the mixed empirical results in the literature summarised in section 6.3, in which both linear and super-linear cumulativity have been observed.
3 Testing for non-linear cumulativity
In this study, we use an AGL task to test whether we can observe non-linear interactions between phonotactic restrictions synchronically in speaker judgements. AGL tasks allow the experimenter to manipulate properties of languages, to perform controlled comparisons of what participants learn under minimally different learning conditions. Such tasks have been used to manipulate the formal complexity (Moreton 2008; Moreton & Pater 2012a; b; Lai 2015; Öttl et al. 2015; McMullin 2016; Avcu & Hestvik 2020) and phonological substance (Wilson 2006; Finley & Badecker 2009; White 2013; Finley 2015; Glewwe 2019) of phonotactic restrictions and alternations. In order to test the effect of the strength of phonotactic restrictions, we can control the probability of individual Markedness violations by introducing exceptions (cf. also Hudson Kam & Newport 2005; Schuler et al. 2021 among many others). This allows us to calculate the joint probability of two violations, and compare it to participants’ acceptability judgements. It also allows us to manipulate those probabilities, to test whether the presence or strength of super-linear interactions depends on the strength of the individual Markedness violations. Finally, we can directly control whether super-linear interactions are present in the training data or not, to test whether learners infer them even in the absence of overt evidence. This approach allows us to make controlled comparisons in a way that is impossible with natural languages. Ultimately, though, we believe that whatever results we observe here should also be confirmed by studies of speakers’ intuitions about how phonotactic restrictions in their native language interact.
Our strategy (following a design employed by Breiss 2020) is to create languages in which two distinct Markedness constraints hold: backness harmony between vowels, and nasal harmony between consonants. This combination of phonotactic restrictions is useful in probing super-linear cumulativity, because they are orthogonal: simultaneous violations of backness and nasal harmony (e.g., [poni]) do not create violations of any other known constraint (see 6.1 for further discussion). In each language, the constraints are enforced with a specific strength, meaning we manipulate the percentage of words that violate them. Participants were trained on mini-lexicons, and then asked to rate novel items that violated neither, one, or both Markedness constraints. What we are interested in measuring is the penalty for doubly-marked forms relative to the singly-marked ones, as modulated by the strength of the phonotactic restrictions.
At this point it is important to note that, just as we cannot experimentally observe and manipulate the weights in a speaker’s grammar, we likewise cannot directly observe the probabilities that the grammar assigns. In general, we assume that grammars assign grammaticality values, which are used to judge the acceptability of linguistic expressions, which in turn guides responses in experimental tasks. The MaxEnt grammar that we employ assigns probabilities to competing candidates. However, experiments do not measure probabilities of candidates directly, but rather, probabilities of responses in a task. For this reason, the relation between grammatical probability and experimentally obtained measurements is necessarily indirect. We seek an experimental effect that bears the hallmarks of the expected grammatical effect. Specifically, we seek an experimental response that allows us to quantify the penalties for forms with individual markedness violations, and use these to predict responses for forms with multiple violations. The expected grammatical effect is that multiply marked forms should be judged worse than expected, based on their individual violations. In the experiments reported here, we have chosen a ratings task as a first way to explore this prediction. Ratings tasks allow us to quantify the penalty for individual violations, by comparing ratings for forms with zero vs. one violation. As described below in section 4, we use linear modeling to predict ratings for doubly marked forms, and we test whether participants’ ratings are lower than expected. Although the computation of expected values in the linear model is mathematically different from the computation of probabilities in the grammatical model, we believe that observing such an effect in ratings is a good first step in testing the super-linearity prediction of the grammatical model.
In Experiment 1, we begin by manipulating the number of exceptions to the two phonotactic restrictions. In this experiment, participants are trained on a lexicon that largely conforms to backness and nasal harmony, but has a certain number of exceptions to each independently (depending on the Condition). In this experiment, doubly-marked forms that violate both backness and nasal harmony are withheld in training, and we then test whether participants rate them exactly as predicted given their judgments about single violations (linear cumulativity), or whether they are rated better/worse (sub-/super-linear cumulativity). At a basic level, this experiment tests whether speakers show non-linear cumulativity in how they enforce restrictions synchronically. It also tests whether the degree of non-linearity depends on the strength of the phonotactics.
The design of Experiment 1 leaves open the possibility that participants exhibit super-linear cumulativity precisely because the doubly-marked forms were absent (withheld). Therefore, in Experiment 2, we test whether participants still exhibit super-linear cumulativity, even when the training language contains exactly as many doubly-marked forms as expected under linear cumulativity. This tests whether speakers are not only able to represent super-linear cumulativity, but whether they are compelled to, even when such forms are not actually underrepresented. We will see that speakers do in fact infer super-linear cumulativity, even when it is not present in the training data.
4 Experiment 1
This experiment tests the relation between the strength of phonotactic restrictions and the type of cumulativity that they produce. The design described in this section was also employed in Breiss (2020), and the results of Experiment 3b of Breiss (2020) are included as Condition A.
4.1 Methods
4.1.1 Stimuli
The exposure phase contained 32 unique CVCV, initially-stressed nonwords, with consonants ∈ {/p, t, m, n/} and vowels ∈ {/i, e, u, o/}. As noted above, one of the two phonotactics was a requirement that consonants harmonize with respect to the feature [nasal], such that both consonants in the word were drawn from either {/p, t/} or {/m, n/} (exhibiting nasal harmony). The other phonotactic required that vowels harmonize with respect to the feature [back], such that both vowels in the word were drawn from either {/i, e/} or {/u, o/} (backness harmony). For more on these types of consonant and vowel harmony respectively, see Hansson (2010); Walker (2011).
Five distinct training Conditions (A-E) were distinguished by the number of items that violated each of the phonotactic patterns in the language: 0%, 6.25%, 12.5%, 18.75% or 25%. There were no training items which violated both phonotactics at once, so even in the most exceptionful Condition (Condition E) each phonotactic received support from 75% of the words in the training phase. Table 4 displays the counts and violation profiles of stimuli.
Distribution of stimuli across Conditions in Experiment 1.
| Condition: | A | B | C | D | E | |
|---|---|---|---|---|---|---|
| Percent exceptions to each phonotactic: | 0% | 6.25% | 12.5% | 18.75% | 25% | |
| No exceptions | potu | 32 | 28 | 24 | 20 | 16 |
| Back exceptions | poti | 0 | 2 | 4 | 6 | 8 |
| Nasal exceptions | ponu | 0 | 2 | 4 | 6 | 8 |
| Doubly-violating | poni | 0 | 0 | 0 | 0 | 0 |
The verification phase used 16 pairs of minimally-differing nonwords: one member of each pair was a fully-conforming word from the exposure phase, and the other was created by reversing the featural specification for backness (and rounding) or nasality of one of the consonants or vowels in the fully-conforming word. This yielded a pair of words differing only in a single instance of that phoneme. 8 pairs differed in a violation of nasal harmony, and 8 in violation of backness harmony, with differences between pair-members balanced for segmental placement and identity. Verification pairs were balanced so that when a fully-conforming verification word had identical consonants (ex. totu), it differed only in the violation of backness harmony (ex., totu vs. toti). The same condition was imposed on verification trials whose conforming word contained identical vowels. There were no doubly-violating words in the verification phase, since its purpose was simply to ensure that participants had learned each of the two phonotactic constraints independently.
The test phase used a set of 48 novel nonwords which varied in conformity to both phonotactics. 24 conformed to both phonotactics (ex. potu), eight violated only the nasal-harmony phonotactic (ex., ponu), eight violated only the backness-harmony phonotactic (poti), and eight violated both the nasal-harmony and backness-harmony phonotactics (poni).
All words were recorded in a sound-attenuated room by a phonetically trained female native English speaker using PCQuirer. They were digitized at 44,100 Hz and normalized for amplitude to 70 dB.
4.1.2 Design
Participants were assigned to one of the five Conditions, and learned the language by listening to a continuous speech stream containing 20 randomized repetitions of the 32 words selected for that particular training phase. After exposure, participants completed 16 self-paced two-alternative forced choice verification trials. Participants were allowed to advance to the generalization phase if they learned each of the phonotactics to a non-significantly-different degree. This was operationalized by imposing a condition that the difference in number of correct answers between pairs differing only in a nasal harmony violation and those differing only in a backness harmony violation was not allowed to be greater than 3, chosen by using Fisher’s exact test (Fisher 1934) to determine the level at which the proportion of correct answers for each phonotactic significantly differed, across the range of possible accuracies. If participants did not meet criteria after two exposure blocks (one initial and one after failing to meet criterion during the verification phase), they were simply asked to complete the final demographic questionnaire and did not generate data in the generalization phase (although we will see in section 4.1.4 that no participants were excluded for this reason).
If participants met criteria on the verification phase, they advanced to a generalization phase which consisted of a ratings task containing 48 novel words in which participants were asked to rate each of the words on a scale from 0 (very bad) to 100 (very good) based on how good they sounded as an example of the language they had learned during the exposure phase. At the end of the experiment, demographic and language-background information was collected. The entire experiment lasted approximately 20–30 minutes, depending on the number of additional exposure blocks each participant required.
4.1.3 Procedure
The experiment was conducted in a sound-attenuated room using a modified version of the Experigen platform (Becker & Levine 2020). At the start of the experiment, participants were informed that they would first be learning a new language, and that they then would be tested on their knowledge of that language. During the exposure phase, participants were instructed to simply sit and listen to the speech stream and, if they felt themselves getting bored, to try to count how many unique words they could find in the speech stream (this task was suggested simply to encourage participants to attend to the speech stream). The exposure phase lasted about ten minutes.
Following the exposure phase, participants completed a self-paced verification phase. On each verification trial participants were played a pair of nonwords in a random order, and were instructed to choose the one that sounded like it could belong to the language they had learned. The generalization phase followed a similar structure, except that each trial containing a single novel nonword to which participants assigned a numerical rating. After completing the generalization phase (or after failure to meet criterion during the verification phase), participants completed a brief demographic questionnaire.
4.1.4 Participants
375 undergraduate students were recruited from the SONA Psychology subject pool at the University of California, Los Angeles, and were compensated with course credit. Participants’ data were excluded if they failed to meet the criterion for sufficient learning as assessed during a verification phase (n = 0; see section 4.1.2 for details), for not having spoken English consistently in some context (home, school, etc.) since early childhood (n = 43), and in the case of experimenter error (n = 3), leaving data from 329 participants included in the final analysis.
4.2 Results
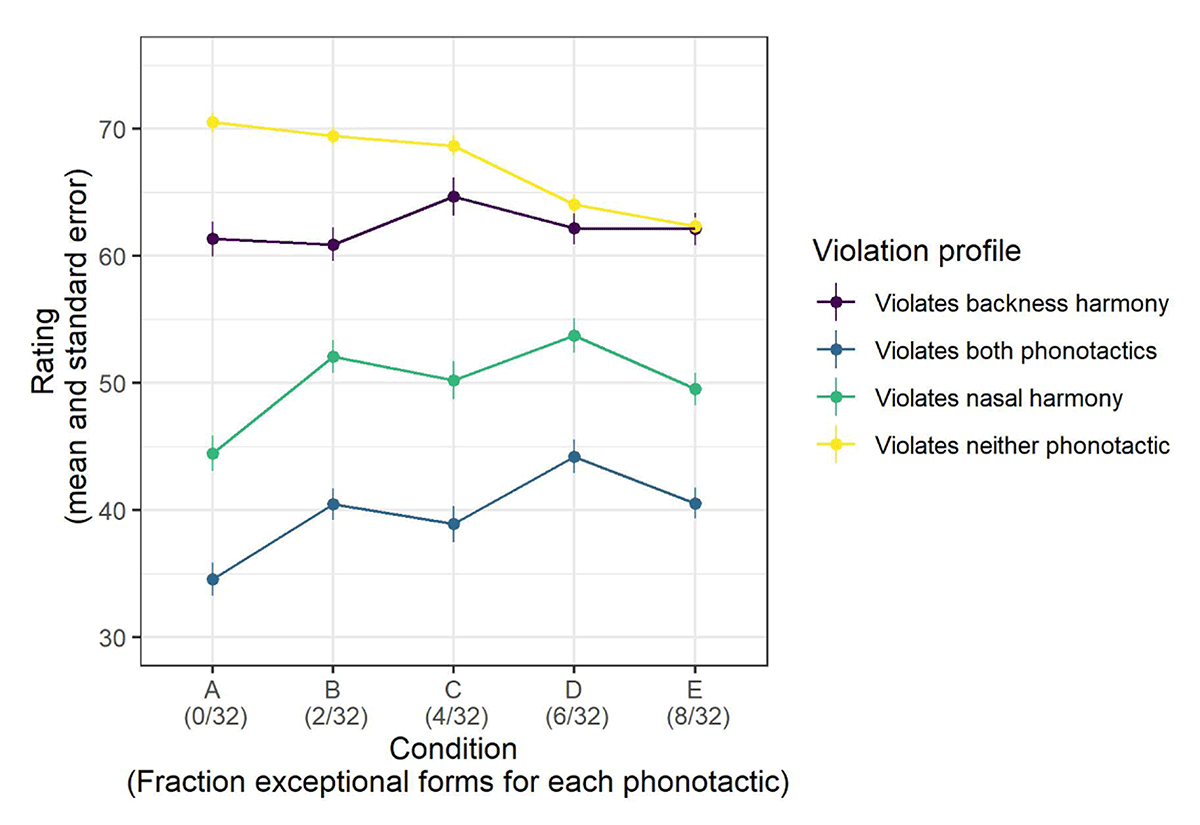
The results from the generalization phase are plotted in Figure 3. As anticipated, stimuli that conform to both restrictions received the highest ratings, stimuli that violated both restrictions received the lowest ratings, and stimuli that violated only one of the two restrictions received intermediate ratings. Furthermore, as the number of exceptions in training increased (Condition A through Condition E), the ratings of violating forms generally increased, as well. Unexpectedly, as the number of exceptions in training increased, the ratings of fully-conforming items also decreased, particularly in Conditions D and E.
As it turns out, although exceptions to backness and nasal harmony were presented with equal frequency in the training data, violations of backness harmony were judged better than violations of nasal harmony, even converging with ratings of fully-conforming items in Conditions D and E. Note that this difference emerged in spite of the fact that, to a first approximation, participants indicated comparable levels of sensitivity to violations of nasal and backness harmony in the verification phase. There are several possible sources of this discrepancy. First, the criterion for comparable accuracy in the verification phase was a difference of 3 responses or less, which translates to a difference of up to ~19%; thus, participants may have learned nasal harmony more strongly and still passed the verification phase. Second, the verification phase involved trained items, whereas the generalization phase involved novel items, so it is conceivable that participants used memory to perform better on backness harmony in the verification phase than in the generalization phase. Finally, it is conceivable that the discrepancy reflects a difference in either the sensitivity of the measures or strategy that participants used to complete the verification vs. generalization tasks.
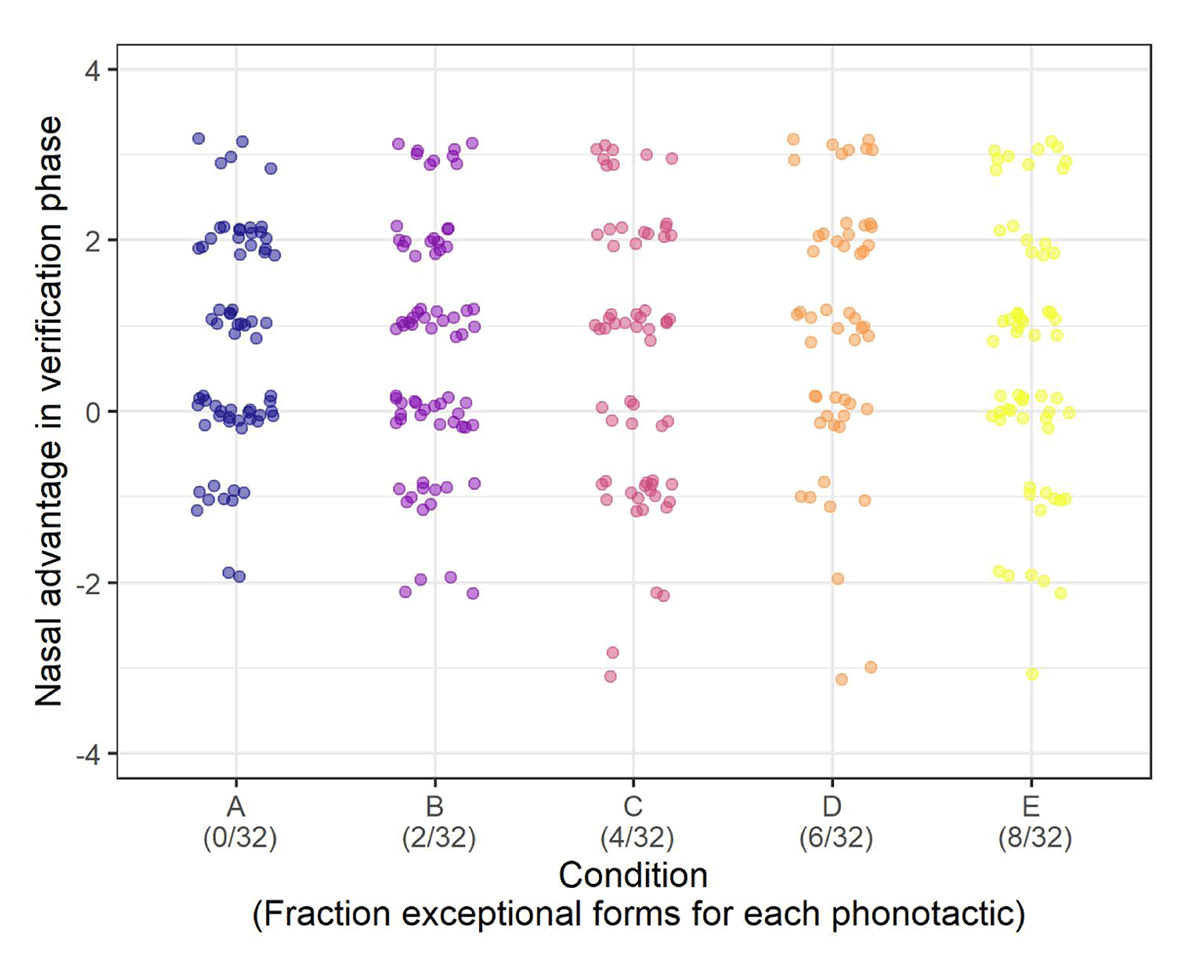
In addition to an overall difference between nasal and backness harmony, the interaction with Condition raises the question of whether the learning of backness harmony was impeded by exceptions in a way that the learning of nasal harmony was not. We can address this in a preliminary way by examining participants’ performance in the verification phase. We calculated each participant’s nasal advantage score, a measure ranging between –3 and 3 which corresponded to the difference between the number of correct answers (out of 8) that participant gave on questions testing backness vs. nasal harmony in the verification phase. A positive score indicates that a participant got more correct answers on the nasal-harmony-assessing questions (ex., potu vs. ponu) than on backness-harmony-assessing questions (potu vs. poti), and a negative score indicates the reverse. If participants were simply not learning the backness-harmony phonotactic, we should expect to see participants in training Conditions with more exceptions having a higher nasal advantage score. Figure 4 plots nasal advantage scores by Condition. A linear model confirmed the visual impression that training Condition (coded as a numerical predictor corresponding to the percentage of training data conforming to both phonotactics) does not significantly predict nasal advantage score (β = – 0.015, p = 0.791). We therefore conclude that although backness harmony was enforced less stringently than nasal harmony – and that this lead to an eventual convergence with fully-conforming items in the most exceptionful Conditions – it is not the case that manipulating the number of exceptions had a differential effect on learning backness vs. nasal harmony.
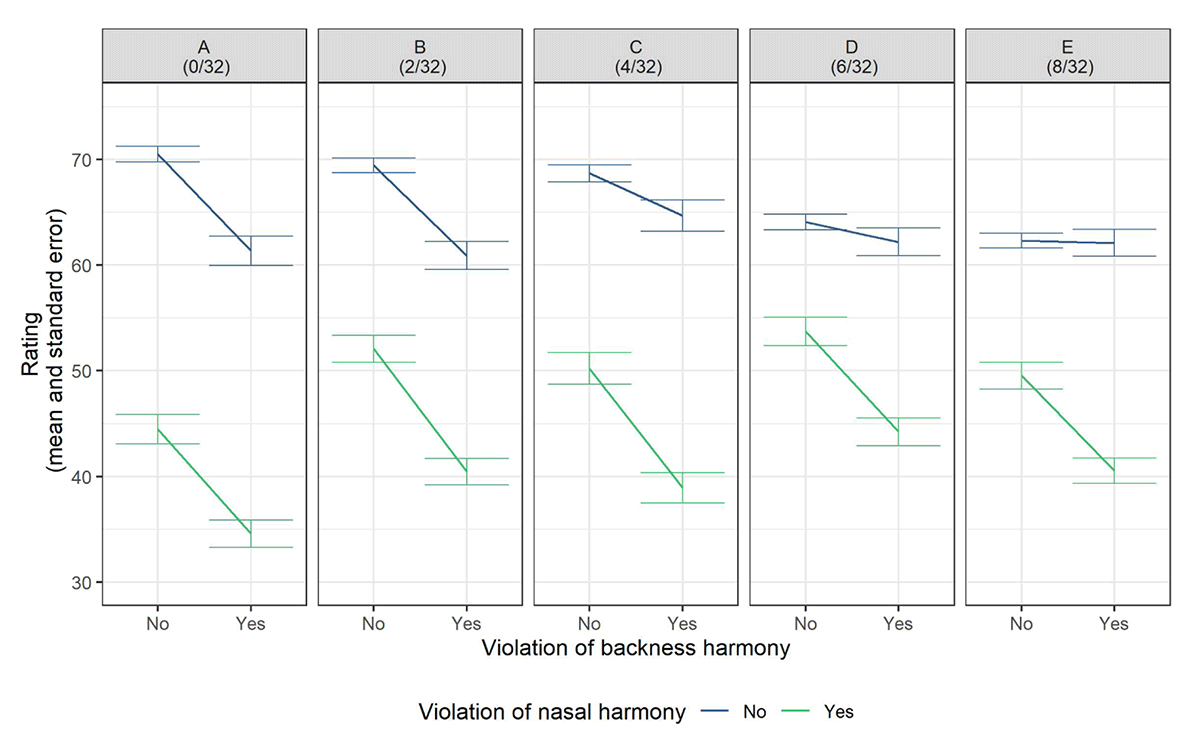
We are now in a position to assess how the the cumulative interaction of nasal and backness harmony varied across Conditions. This interaction is seen in the re-plotted data in Figure 5, which shows a gradual divergence in the slopes of the two lines representing the effect of nasal harmony, in the presence or absence of backness harmony violations.
Recall from section 2.1 that we define linear cumulativity as the scenario where each Markedness violation has its own independent effect on the well-formedness of a form, independent of any other violations present. Conversely, non-linear cumulativity means that certain combinations of violations yield a greater reduction in well-formedness than we could deduce from the sum of their violations alone. Statistically speaking, this means that we first fit a model of participants’ ratings, in which we attempt to predict a form’s rating as a function of its (non-)conformity to backness and nasal harmony, independently. Specifically, we fit a linear mixed effects regression model using the lme4 package (Bates et al. 2015) in R (R Core Team 2021), modeling the ratings data from the generalization phase. In this model, each constraint violation constitutes a main effect, with the possibility that it may combining forces with another constraint violation (an interaction). Thus, the model included fixed effects for the two Markedness constraints: violation of vowel harmony (y/n, reference level = n) and violation of consonant harmony (y/n, reference level = n). We can assess the linearity of constraint cumulativity by looking at whether the interaction between the markedness effects is significantly different from zero; the interaction term indicates the degree to which the rating is ill-formed above and beyond the contribution attributable to each of the component violations independently. Finally, we are interested in not only the cumulativity of any two violations per se but also the relationship between the strength of the individual constraints (Conditions A–E) and the cumulativity of those constraints. Therefore, we also included a continuous fixed effect corresponding to the percentage of exceptions to individual phonotactics in a given participants’ training Condition. We are crucially interested in the three-way interaction between the two phonotactic violations and Condition: if it is significantly negative, that means that the penalty for doubly-violating forms is greater than can be accounted for based on the independent penalties for each violation. We will take such an interaction as initial support for a model that produces super-linear cumulativity. Recall from section 3 that this way of calculating deviations from expected grammaticality is not identical to the probability-based definition given in section 2.3, but what they have in common is that a response value (probability, rating) for doubly marked forms is lower than expectations based on singly marked forms.
Following Barr et al. (2013), we began by fitting a model with a maximally-specified random effect structure and simplified as necessary to achieve convergence. The final model contained the three-way interaction between the fixed effects outlined above, plus random intercepts for participant and nonword.
This model revealed that violating the nasal harmony phonotactic was associated with significantly lower ratings (β = –24.93, p < 0.001). The interaction between violation of nasal harmony and Condition was significant (β = 0.29, p < 0.001), indicating that as the percentage of forms violating the nasal harmony phonotactic in the training data increased, novel forms which violated this phonotactic were judged less ill-formed. The analogous main effects and interaction between violation of the backness harmony phonotactic and training group was also significant (main effect: β = –9.95, p = 0.015; interaction: β = 0.19, p < 0.001). There was also a significant main effect of training group, indicating that as as the number of fully-conforming words heard in training decreased, fully-conforming words were judged less well-formed as a baseline (β = –0.18, p < 0.001). Critically, the three-way interaction between violation of nasal harmony, violation of backness harmony, and Condition was significant (β = –0.17, p < 0.002). The negative coefficient indicates that as the percentage of nonconforming words in training increased, the difference between singly-marked and unmarked items decreased, while the relative markedness associated with the doubly-marked items remained approximately unchanged.
4.3 Local discussion
Experiment 1 found that speakers are able to represent super-linear patterns in their grammar, and that this super-linearity is related to the strength of the phonotactic restrictions involved. We found that as the number of exceptions in the training increased, learners judged doubly-violating items as more and more ill-formed than one would expect, based on their judgements of singly-violating forms. These results are consistent with the proposed model that is able to represent super-linear cumulativity under particular weighting conditions.
Experiment 1 manipulated the number of forms that violated each phonotactic restriction; that is, we introduced violations of backness harmony (ex., poti) and of nasal harmony (ex., ponu). A by-product of this manipulation was that the Conditions also differed in the expected rate of doubly-violating forms — that is, forms that violated both backness and nasal harmony simultaneously, like poni. Recall that the expected rate of doubly-violating forms is the product of the probabilities of each individual violation. For Condition A, with zero exceptions, the rate of one violation is 0%, and the expected rate of two violations is 0%2 = 0%. For Condition E, on the other hand, the rate of single violations is 25%, and the expected rate of two violations is 25%2 = 6.25%, or 2 words in a lexicon of 32 words. However, such doubly-violating forms were withheld completely in training for all Conditions, since we were interested in testing participants’ judgments about an untrained word type. This raises the possibility that learners were sensitive to the lack of doubly-violating forms, particularly in Conditions D and E, and used this to learn a grammar that specifically penalized them.
Does our MaxEnt + Null Parse model allow for the above suggestion of super-linear cumulativity via overt learning? Here, the expected degree of super-linearity is a function of the weights of the constraints involved. Figure 2 shows that for most weights of MParse, the model predicts that as the weight of Markedness decreases — and the probability of singly-violating forms correspondingly increases — the penalty for multiply-violating forms becomes super-linear. If the weight of MParse is invariant, the degree of super-linearity should be an emergent by-product of the strength of the phonotactic restrictions. Other models allow a broader range of cumulative effects through additional parameters. If the weight of MParse is variable, learners would be able to capture a wider (though still quite constrained) range of linear or non-linear effects by setting the weight of MParse in response to the data. An even more powerful approach is to induce a conjoined constraint, such as Agree[±back] & Agree[±nasal], which allows for any degree of super-linearity (Smolensky 1993; Ito & Mester 2003; Shih 2017: see section 6.1 for further discussion). The question, then, is whether learners in Experiment 1 noticed the one or two missing forms and used highly parameterized grammars to accommodate super-linearity, or whether they projected it as a by-product of enforcing the individual restrictions. We address this question in Experiment 2.
5 Experiment 2
We carried out a replication of Condition E from Experiment 1, except that the training data included two doubly-violating forms, so that they were no longer underrepresented in the training data. If this experiment finds linear cumulativity, we can conclude that the super-linear effect observed in Experiment 1 Condition E was due to the lack of doubly-violating forms, suggesting overt learning. If we nonetheless observe super-linear cumulativity, we can conclude that learners project super-linear cumulativity of weak phonotactic restrictions, even when this deviates from the observed frequencies.4
5.1 Methods
The stimuli, design, and procedure for Experiment 2 were identical to those of Experiment 1 Condition E, except that two of the singly-violating forms were altered so as to also violate the other phonotactic; see Table 5. 86 undergraduate students were recruited from the same subject pool to participate in the experiment, and were compensated for their time with course credit. Of these, 15 were excluded for not having spoken English consistently in some context since before the age of seven, leaving data from 71 participants for analysis.
Distribution of training items by type, comparing Experiment 1 Condition E to Experiment 2.
| Experiment: | 1E | 2 | |
|---|---|---|---|
| Unmarked | potu | 16 | 16 |
| Back exceptions | poti | 8 | 8 |
| Nasal exceptions | ponu | 8 | 8 |
| Doubly-violating | poni | 0 | 2 |
5.2 Results
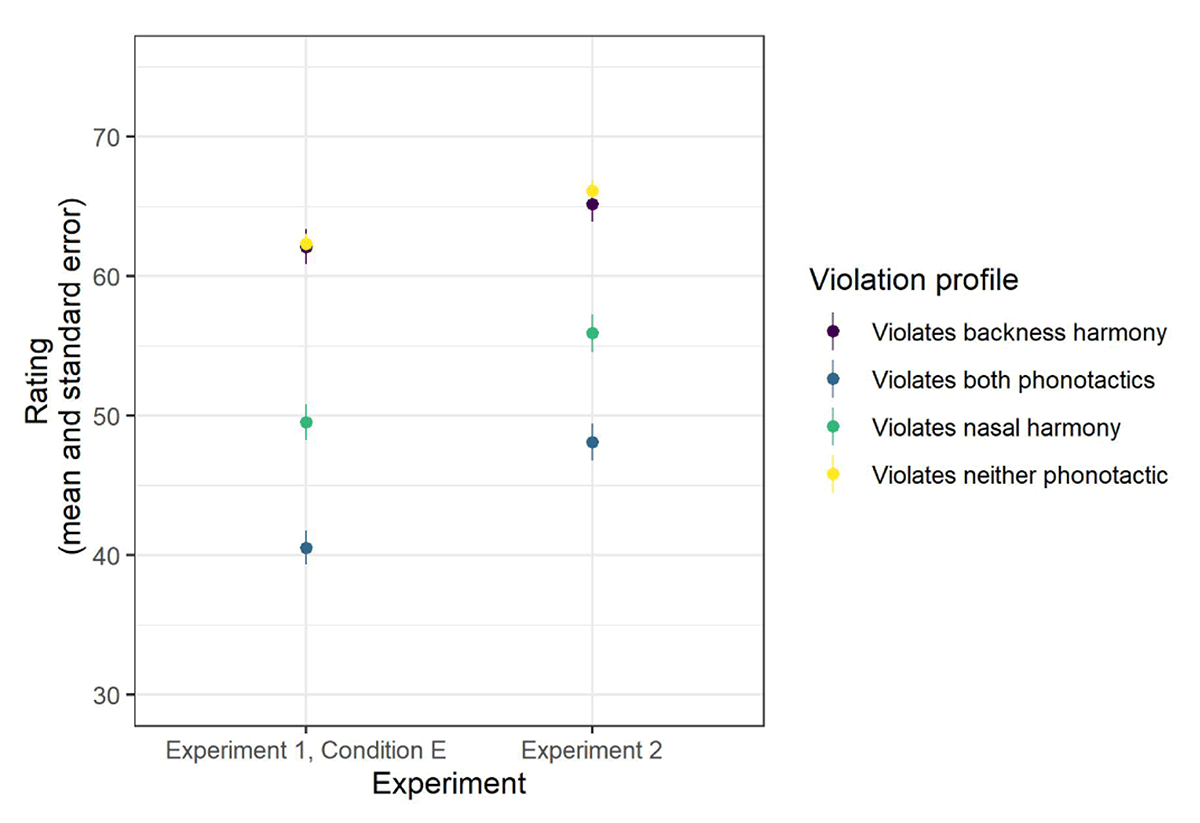
The results of Experiment 2 are shown in Figure 6. Comparing Experiment 1 Condition E and Experiment 2, we see that in both cases, participants rated forms that violated neither phonotactic restriction were rated highest, and forms that violated backness harmony were rated essentially as high. Forms that violated nasal harmony were rated lower, while forms that violated both nasal and backness harmony received lower ratings still. As above, the question of interest is whether the penalty for violating both nasal and backness harmony continued to be greater than expected (super-linear) in Experiment 2, based on the independent penalties associated with each individual violation.
To test this, we analyzed the two datasets together in a mixed-effects linear regression model. Since we anticipate a null result, in contrast to Experiment 1 we opted for a Bayesian implementation of the model, using the brms package (Bürkner et al. 2017).5 Bayesian models estimate a range of probable values for the parameters of interest; thus we can conclude that an effect is robust to the extent that 95% of these values, a measure known as a 95% Credible Interval (abbreviated to “95% CI”, followed by upper and lower bounds in square brackets), does not include zero. The inverse of this is that if the range is centered on zero, then we can say there is evidence for no effect of the parameter of interest on the dependent variable. Thus, the Bayesian model allows us to present evidence that supports, rather than simply fails to reject the null hypothesis. For a linguistically-oriented introduction to Bayesian methods for both theory-building and data analysis, see Nicenboim & Vasishth (2016); for tutorial materials on the brms package in a linguistic context, see Vasishth et al. (2018); Nalborczyk et al. (2019); for a more general primer in Bayesian statistical modeling, see Kruschke (2014).
As in Experiment 1, the dependent variable was the numerical rating given to each word in the generalization phase. Also as in Experiment 1 the model contained a fixed effect of whether the form violated backness harmony (y/n, reference level = n), whether the form violated nasal harmony (y/n, reference level = n), and a binary factor for Experiment (one/two, reference level = one), as well as all two- and three-way interactions of these predictors. The model also contained random intercepts for nonword with slopes for Experiment, and random intercepts for subject with slopes for the interaction of the two binary phonotactic predictors.
We can interpret the output of the model as follows: if the 95% Credible Interval for the three-way interaction of violating backness harmony, violating nasal harmony, and Experiment excludes zero, it indicates that the degree of linearity in the cumulative interaction of violating both phonotactics together compared to their independent violations differed meaningfully between studies. If the 95% Credible Interval for the interaction is centered on zero, we can conclude that the cumulative effect of violating both phonotactics did not differ between studies, and thus was unlikely to have been overtly learned in Experiment 1.
Violating nasal harmony resulted in lower ratings (β = –12.72, 95% CI [–21.49, –3.85]), while the effect of violating backness harmony did not (β = –0.10, 95% CI [–8.91, 8.72]). One experiment was not reliably associated with higher ratings than the other overall (β = 3.89, 95% CI [–0.87, 8.35]). The coefficient for the interaction between violating backness and nasal harmony did not differ meaningfully from zero (β = –8.87, 95% CI [–22.44, 4.96]), nor did the coefficient for the interaction between Experiment and violating backness harmony (β = –0.72, 95% CI [–4.50, 2.96]), nor did the coefficient for the interaction between Experiment and violating nasal harmony (β = 2.56, 95% CI [–2.30, 7.22]). Turning to the quantity of interest, the credible intervals for coefficient of the three-way interaction between violating backness harmony, violating nasal harmony, and Experiment surrounded around zero (β = 1.89, 95% CI [–4.13, 7.73]).
5.3 Local discussion
Experiment 2 tested for whether the super-linear cumulativity observed in Experiment 1 was a result of participants overtly learning a super-linear penalty from the super-linear underrepresentation in their data. We found that the linearity of cumulativity was not affected by whether or not the training data contained a subtle super-linear pattern. We take this to be compelling evidence in support a synchronic link between exceptionality in learning data and super-linear cumulativity, as discussed in section 2, and against the possibility of the effect having been overtly learned.
6 Discussion
The experimental results in this study have shown that speakers can enforce super-linear cumulativity between phonotactic restrictions as a synchronic effect, and in fact even assume super-linearity under certain conditions, even when it is not present in the data. Using AGL experiments, we first systematically varied the number of exceptions to phonotactic restrictions in training, and found that the degree of non-linearity depends on the strength of those restrictions in the grammar. We then varied the amount of evidence that learners received for super-linear cumulativity in the training data, and found that learners continued to exhibit it even when such evidence was removed entirely.
On the basis of these data, we conclude that speakers can represent super-linear cumulativity in their synchronic grammar, and that this super-linearity was emergent from the interaction of the two constraints — a property of the grammar itself — rather than overtly learned from the training data.
6.1 Super-linear cumulativity or one constraint?
In our experimental results, we observe an interaction between two harmony restrictions: backness of vowels and nasality of consonants. We have assumed that these restrictions are enforced by separate Markedness constraints, and that the observed effect must reflect a super-linear interaction between two constraints. It is crucial for this interpretation that it is not due to the action of a single constraint, “nasal and backness CV harmony”, which penalizes only those sequences which violate both independent Agree constraints. Thus, it is important to consider whether participants were employing such a unitary constraint.
There are two ways of thinking about a putative “nasal and backness CV harmony” constraint. On the one hand, it could be a unitary constraint enforcing simultaneous agreement of consonant nasality and vowel backness. On the other hand, it could be a conjoined constraint, Agree[±back] & Agree[±nas] (Smolensky 1993; Ito & Mester 2003).6 In either case, we have no particular reason to believe that there is such a constraint, since we know of no formal, phonetic, or typological connection between these two restrictions. More importantly, even if such a constraint existed, it would be mysterious why participants in Experiment 2 inferred its presence or activity, since we removed any trace of nasal plus backness harmony from speakers’ learning data. We therefore conclude that the effects that we observe involve super-linear cumulativity of two separate constraints.
6.2 Whence super-linearity? MParse and beyond
We have based much of the framing of this paper on a model of phonotactic acceptability in which each form competes against a Null Parse candidate for existence, and then this probability is mapped onto a rating given by the participant. We illustrated this using a MaxEnt model, in which super-linearity emerges as a consequence of how probability is calculated from Harmony. We adopted the MaxEnt framework because it is easy to demonstrate how it derives super-linearity, but similar effects can be derived in other probabilistic constraint-based models, too, such as Noisy Harmonic Grammar (Boersma & Pater 2016; Hayes 2017; Smith & Pater 2020). We do not believe that the current results uniquely support a MaxEnt model, though they are consistent with it.
A distinguishing feature of this model that does play an important role in deriving super-linearity is the use of MParse. In most existing frameworks, unacceptability is modeled with grammars that assign low probability to a form, and high probability to a competitor — either an unfaithful rendition of the UR (Prince & Smolensky 1993) or other competitor strings which are more probable (Hayes & Wilson 2008). In models that employ MParse, unacceptability may also be modeled as the selection of the Null Parse, which violates only a single constraint (Prince & Smolensky 1993; Smolensky 1993; Wolf & McCarthy 2010). In the model illustrated in section 2.1, we crucially assumed that the Null Parse is not only a competing candidate, but the only competing candidate. This allows for the grammar to set a threshold of markedness above which the marked form is quite probable, and below which the Null Parse quickly becomes the more favored candidate (see also footnote 9 in Legendre et al. 1998). This thresholding effect is not so readily available in models that have candidate sets in which Markedness and Faithfulness violations trade off against each other in a one-to-one manner (Pater 2009b), or models which are based on the relative Harmony of different non-null candidates, such as the model proposed in Hayes & Wilson (2008).
A consequence of choosing this model is that, since it lacks Faithfulness, it cannot model any process in which a string must be repaired, such as alternations, loanword adaptation, and others. This leaves open the question of how to model such phenomena. The question of how closely tied phonological repairs are to phonotactic restrictions is an area of long-standing debate (Sommerstein 1974; McCarthy 2002: p. 77; Pizzo 2015; Chong 2017; Do & Yeung 2021). We see several possible answers to this question that can accommodate super-linearity in phonotactics, while also producing repairs. One is that phonotactic acceptability and phonological alternations are completely separate processes, as suggested by Hayes & Wilson (2008). However, our use of MParse does not require two separate grammars. Phonotactic restrictions and repairs could be derived with a single grammar, with a single set of Markedness constraints and weights, but in which different candidate sets are considered in different contexts or for different tasks. For example, we could model phonotactic acceptability judgments as a competition between the fully faithful candidate and the Null Parse, in which MParse is the arbiter. Alternations, on the other hand, could be modeled as a competition between the fully faithful candidate and possible repairs, decided by Faithfulness constraints.
6.3 Super-linearity vs. sub-linearity
The model that we have explored here has the ability to capture both linear and super-linear cumulativity, but in a restricted fashion: as seen in Figure 2, the degree of cumulativity depends on the strength of the phonotactic restrictions involved. This is precisely what we observed in our experimental results. The fact that the very same phonotactic restrictions can interact in different ways depending on their strength has the potential to shed light on a discrepancy in the literature, between studies that do (Albright 2008; 2012; Green & Davis 2014; Kumagai 2017; Shih 2017; Yang et al. 2018; Kim 2019; Smith & Pater 2020) and do not (Pizzo 2015; Breiss 2020; Durvasula & Liter 2020; Kawahara 2021; Kawahara & Breiss 2021; Kawahara & Moore 2021) observe super-linearity.
Figure 2 predicts exactly the type of transition we observed: as we move upwards along the vertical axis from a stronger to a weaker phonotactic restriction, we observe a transition from one type of interaction to another, and the specific transition depends on the weight of MParse. For most values of MParse, the prediction is a shift from linear to super-linear interactions, as in our experiments. However, for some values of MParse, the model also predicts a region of sub-linear cumulativity. In fact, there are possible indications of sub-linear cumulativity in the literature: Pizzo (2015) found that violations of syllable-margin restrictions in English interacted sub-linearly in phonotactic acceptability. It is conceivable, therefore, that the apparently discrepant results in the literature are simply a consequence of the weights of markedness and MParse involved. Continued systematic experimental investigation of how phonotactic restrictions of varying strengths interact will reveal whether linearity, super-linearity, and sub-linearity emerge under the predicted weighting conditions. AGL tasks like the one employed here are a useful tool for probing this question, because they allow us to vary phonotactic strength independent of other properties of the language.
7 Conclusion
The work presented here is a first step towards a fuller understanding of the empirical and typological landscape of (non-)linear cumulativity. The dependency between constraint strength and cumulative behavior proposed by our model makes strong predictions about both the wide scope of constraints that can enter into non-linear cumulative relationships, and also specific claims about the weighting requirements that must be met for such effects to be observed. A great deal of further empirical research is therefore needed to test and refine these predictions going forward.
Supplementary files
Appendix Conditions on linearity in MaxEnt. DOI: https://doi.org/10.16995/glossa.5713.s1
Anonymized response data from both experiments. DOI: https://doi.org/10.16995/glossa.5713.s2
Notes
- The term super-linear is used even though the probability or acceptability is lower than expected, because the penalty is higher than expected under linear combination. [^]
- Note that the distinction that Jäger & Rosenbach (2006) make between counting and ganging cumulativity is orthogonal to the current discussion of different degrees of cumulativity — linear, sub-linear, or super-linear. [^]
- When the competition is defined as a two-way choice between the faithful output and the Null Parse, we avoid the “trading off” relations between Markedness and Faithfulness constraints observed by Pater (2009b), thus permitting a wider range of super-linear interactions. Note that the same type of effect can be observed in the interaction of multiple Markedness constraints with a single Faithfulness constraint, as in Smith & Pater (2020)’s analysis of French schwa epenthesis and deletion. [^]
- We leave open whether learners project super-linearity because their grammatical mechanism is so tightly parameterized that the degree of linearity in cumulativity is necessarily determined by the strength of the restrictions, or whether they project it due to prior expectations about constraint weights that yield super-linearity of weak phonotactic restrictions. In order to address this, we would need provide learners with more evidence for super-linearity; for example, a larger number of forms, so that the discrepancy between observed and expected numbers of doubly-marked forms would be greater. [^]
- The model we fit used default weakly-informative priors, with a burn-in period of 1000 iterations followed by a sampling period of 1000 iterations. We ran four chains to ensure thorough exploration of the posterior distribution, and all Rˆ values were between 1 and 1.01, indicating that the chains mixed successfully. [^]
- Numerous authors have pointed out that local constraint conjunction has the potential to radically expand the predicted phonological typology beyond what has been observed (Pater 2009a; b; Potts et al. 2010). Moreover, the putative constraint Agree[±back] & Agree[±nas] pushes the limits of what is allowed for constraint conjunction, since the locus of violation spans multiple segments and syllables (Łubowicz 2005). [^]
Ethics and consent
All experiments reported in this paper were carried out with the approval of the IRB board at the University of California, Los Angeles.
Acknowledgements
Thanks to Bruce Hayes, Gaja Jarosz, Giorgio Magri, Kie Zuraw, Claire Moore-Cantwell, two anonymous Glossa reviewers and Associate Editor Björn Köhnlein, and members of audiences at the 2020 LSA Annual Meeting and the UCLA Phonology Seminar for helpful discussion and feedback. Thanks also to Beth Sturman for recording stimuli, and to Ruby Dennis, Gabrielle Dinh, Shreya Donepudi, Grace Hon, Lakenya Riley, Azadeh Safakish, and Amanda Singleton for helping to run subjects. Full responsibility for all remaining errors rests with the authors.
Funding information
This work was supported by NSF Graduate Research Fellowship DGE-1650604 to the first author.
Competing interests
The authors have no competing interests to declare.
References
Albright, Adam. 2008. Cumulative violations and complexity thresholds. Unpublished ms, MIT.
Albright, Adam. 2012. Additive markedness interactions in phonology. Colloquium talk at UCLA. https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.436.8618&rep=rep1&type=pdf.
Avcu, Enes & Hestvik, Arild. 2020. Unlearnable phonotactics. Glossa 5(1). DOI: http://doi.org/10.5334/gjgl.892
Baayen, R. Harald & Piepenbrock, Richard & Gulikers, Leon. 1996. The celex lexical database (cd-rom).
Bailey, Todd M. & Hahn, Ulrike. 2001. Determinants of wordlikeness: Phonotactics or lexical neighborhoods? Journal of Memory and Language 44(4). 568–591. DOI: http://doi.org/10.1006/jmla.2000.2756
Barr, Dale J. & Levy, Roger & Scheepers, Christoph & Tily, Harry J. 2013. Random effects structure for confirmatory hypothesis testing: Keep it maximal. Journal of memory and language 68(3). 255–278. DOI: http://doi.org/10.1016/j.jml.2012.11.001
Bates, Douglas & Mächler, Martin & Bolker, Ben & Walker, Steve. 2015. Fitting linear mixed-effects models using lme4. Journal of Statistical Software 67(1). 1–48. DOI: http://doi.org/10.18637/jss.v067.i01
Becker, Michael & Ketrez, Nihan & Nevins, Andrew. 2011. The surfeit of the stimulus: Analytic biases filter lexical statistics in Turkish laryngeal alternations. Language, 84–125. DOI: http://doi.org/10.1353/lan.2011.0016
Becker, Michael & Levine, Jonathan. 2020. Experigen: an online experiment platform https://github.com/tlozoot/experigen.
Beguš, Gašper. 2018. Unnatural phonology: A synchrony-diachrony interface approach: Harvard University dissertation.
Boersma, Paul & Hayes, Bruce. 2001. Empirical tests of the gradual learning algorithm. Linguistic inquiry 32(1). 45–86. DOI: http://doi.org/10.1162/002438901554586
Boersma, Paul & Pater, Joe. 2016. Convergence properties of a gradual learning algorithm for harmonic grammar.
Boersma, Paul et al. 1997. How we learn variation, optionality, and probability. In Proceedings of the institute of phonetic sciences of the university of amsterdam 21. 43–58. Amsterdam.
Breiss, Canaan. 2020. Constraint cumulativity in phonotactics: evidence from artificial grammar learning studies. Phonology 37(4). 551–576. DOI: http://doi.org/10.1017/S0952675720000275
Bürkner, Paul-Christian et al. 2017. brms: An R package for Bayesian multilevel models using Stan. Journal of statistical software 80(1). 1–28. DOI: http://doi.org/10.18637/jss.v080.i01
Chong, Junxiang Adam. 2017. On the relation between phonotactic learning and alternation learning: UCLA dissertation.
Coetzee, Andries W. 2004. What it means to be a loser: Non-optimal candidates in optimality theory. University of Massachusetts Amherst dissertation.
Do, Y. & Yeung, P. 2021. Evidence against a link between learning phonotactics and learning phonological alternations. Linguistics Vanguard. DOI: http://doi.org/10.1515/lingvan-2020-0127
Durvasula, Karthik & Liter, Adam. 2020. There is a simplicity bias when generalising from ambiguous data. Phonology 37(2). 177–213. DOI: http://doi.org/10.1017/S0952675720000093
Finley, Sara. 2015. Learning nonadjacent dependencies in phonology: Transparent vowels in vowel harmony. Language 91(1). 48. DOI: http://doi.org/10.1353/lan.2015.0010
Finley, Sara & Badecker, William. 2009. Artificial language learning and feature-based generalization. Journal of memory and language 61(3). 423–437. DOI: http://doi.org/10.1016/j.jml.2009.05.002
Fisher, Ronald Aylmer. 1934. Two new properties of mathematical likelihood. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character 144(852). 285–307. DOI: http://doi.org/10.1098/rspa.1934.0050
Flemming, Edward. 2021. Comparing maxent and noisy harmonic grammar. Glossa: a journal of general linguistics 6(1). DOI: http://doi.org/10.16995/glossa.5775
Frisch, Stefan. 1996. Similarity and frequency in phonology: dissertation.
Frisch, Stefan A. & Pierrehumbert, Janet B. & Broe, Michael B. 2004. Similarity avoidance and the OCP. Natural Language & Linguistic Theory 22(1). 179–228. DOI: http://doi.org/10.1023/B:NALA.0000005557.78535.3c
Glewwe, Eleanor. 2019. Bias in phonotactic learning: Experimental studies of phonotactic implicationals: UCLA dissertation.
Goldwater, Sharon & Johnson, Mark. 2003. Learning OT constraint rankings using a maximum entropy model. In Proceedings of the stockholm workshop on variation within optimality theory, vol. 111120.
Green, Christopher R. & Davis, Stuart. 2014. Superadditivity and limitations on syllable complexity in bambara words. Perspectives on phonological theory and development, in honor of Daniel A. Dinnsen. 223–47. DOI: http://doi.org/10.1075/lald.56.17gre
Hansson, Gunnar Ólafur. 2010. Consonant harmony: Long-distance interactions in phonology, vol. 145. University of California Press.
Hayes, Bruce. 2017. Varieties of noisy harmonic grammar. In Proceedings of the annual meetings on phonology, vol. 4. DOI: http://doi.org/10.3765/amp.v4i0.3997
Hayes, Bruce & White, James. 2013. Phonological naturalness and phonotactic learning. Linguistic Inquiry 44(1). 45–75. DOI: http://doi.org/10.1162/LING_a_00119
Hayes, Bruce & Wilson, Colin. 2008. A maximum entropy model of phonotactics and phonotactic learning. Linguistic inquiry 39(3). 379–440. DOI: http://doi.org/10.1162/ling.2008.39.3.379
Hudson Kam, Carla L. & Newport, Elissa L. 2005. Regularizing unpredictable variation: The roles of adult and child learners in language formation and change. Language learning and development 1(2). 151–195. DOI: http://doi.org/10.1080/15475441.2005.9684215
Ito, Junko & Mester, Armin. 2003. On the sources of opacity in ot: Coda processes in german. 271–303. Cambridge University Press. DOI: http://doi.org/10.1017/CBO9780511497926.012
Jäger, Gerhard & Rosenbach, Anette. 2006. The winner takes it all—almost: Cumulativity in grammatical variation. Linguistics 44(5). 937–971. DOI: http://doi.org/10.1515/LING.2006.031
Jurafsky, Daniel & Martin, James H. 2009. Speech and language processing: An introduction to natural language processing, computational linguistics, and speech recognition, 2nd edition. Prentice Hall.
Kawahara, Shigeto. 2021. Testing maxent with sound symbolism: A stripy wug-shaped curve in Japanese pokémon names. Language (Research Reports). DOI: http://doi.org/10.1353/lan.2021.0081
Kawahara, Shigeto & Breiss, Canaan. 2021. Exploring the nature of cumulativity in sound symbolism: Experimental studies of Pokémonastics with English speakers. Laboratory Phonology: Journal of the Association for Laboratory Phonology 12(1). DOI: http://doi.org/10.5334/labphon.280
Kawahara, Shigeto & Kumagai, Gajuki. 2021. Does Lyman’s Law count? Natural Language & Linguistic Theory Manuscript submitted for review.
Kawahara, Shigeto & Moore, Jeff. 2021. How to express evolution in English pokémon names. Linguistics 59(3). 577–607. DOI: http://doi.org/10.1515/ling-2021-0057
Kim, Seoyoung. 2019. Modeling self super-gang effects in MaxEnt: A case study on Japanese Rendaku. Talk at NELS 2019.
Kruschke, John. 2014. Doing bayesian data analysis: A tutorial with r, jags, and stan. Academic Press. DOI: http://doi.org/10.1016/B978-0-12-405888-0.00008-8
Kumagai, Gakuji. 2017. Super-additivity of OCP-nasal effect on the applicability of Rendaku. Presentation at GLOW in Asia 2017.
Lai, Regine. 2015. Learnable vs. unlearnable harmony patterns. Linguistic Inquiry 46(3). 425–451. DOI: http://doi.org/10.1162/LING_a_00188
Legendre, Géraldine & Miyata, Yoshiro & Smolensky, Paul. 1990. Harmonic grammar: A formal multi-level connectionist theory of linguistic well-formedness: Theoretical foundations. Citeseer.
Legendre, Géraldine & Smolensky, Paul & Wilson, Colin. 1998. When is less more? Faithfulness and minimal links in wh-chains. Is the best good enough? 249–289.
Łubowicz, Anna. 2005. Locality of conjunction. In Alderete, Han C. & Kochetov A., J. (ed.), Proceedings of wccfl 24. 254–262.
Martin, Andrew. 2011. Grammars leak: Modeling how phonotactic generalizations interact within the grammar. Language 87(4). 751–770. DOI: http://doi.org/10.1353/lan.2011.0096
Martin, Andrew Thomas. 2007. The evolving lexicon: UCLA dissertation.
McCarthy, John J. 2002. A thematic guide to optimality theory. Cambridge University Press. DOI: http://doi.org/10.1017/CBO9780511613333
McMullin, Kevin James. 2016. Tier-based locality in long-distance phonotactics: learnability and typology: University of British Columbia dissertation.
Moreton, Elliott. 2008. Analytic bias and phonological typology. Phonology 25(1). 83–127. DOI: http://doi.org/10.1017/S0952675708001413
Moreton, Elliott & Pater, Joe. 2012a. Structure and substance in artificial-phonology learning, part I: Structure. Language and linguistics compass 6(11). 686–701. DOI: http://doi.org/10.1002/lnc3.363
Moreton, Elliott & Pater, Joe. 2012b. Structure and substance in artificial-phonology learning, part II: Substance. Language and linguistics compass 6(11). 702–718. DOI: http://doi.org/10.1002/lnc3.366
Nalborczyk, Ladislas & Batailler, Cédric & Loevenbruck, Hélène & Vilain, Anne & Bürkner, Paul-Christian. 2019. An introduction to Bayesian multilevel models using brms: A case study of gender effects on vowel variability in standard Indonesian. Journal of Speech, Language, and Hearing Research 62(5). 1225–1242. DOI: http://doi.org/10.1044/2018_JSLHR-S-18-0006
Nicenboim, Bruno & Vasishth, Shravan. 2016. Statistical methods for linguistic research: Foundational Ideas — Part II. Language and Linguistics Compass 10(11). 591–613. DOI: http://doi.org/10.1111/lnc3.12207
Öttl, Birgit & Jäger, Gerhard & Kaup, Barbara. 2015. Does formal complexity reflect cognitive complexity? Investigating aspects of the Chomsky hierarchy in an artificial language learning study. PloS one 10(4). e0123059. DOI: http://doi.org/10.1371/journal.pone.0123059
Pater, Joe. 2009a. Paul Smolensky and Géraldine Legendre (2006). The harmonic mind: from neural computation to optimality-theoretic grammar. Cambridge, Mass.: MIT Press. Vol. 1: Cognitive architecture. Pp. xxiv+ 563. Vol. 2: Linguistic and philosophical implications. Pp. xxiv+ 611. Phonology 26(1). 217–226. DOI: http://doi.org/10.1017/S0952675709001766
Pater, Joe. 2009b. Weighted constraints in generative linguistics. Cognitive science 33(6). 999–1035. DOI: http://doi.org/10.1111/j.1551-6709.2009.01047.x
Pizzo, Presley. 2015. Investigating properties of phonotactic knowledge through web-based experimentation: dissertation.
Potts, Christopher & Pater, Joe & Jesney, Karen & Bhatt, Rajesh & Becker, Michael. 2010. Harmonic grammar with linear programming: from linear systems to linguistic typology. Phonology 27(1). 77–117. DOI: http://doi.org/10.1017/S0952675710000047
Prince, Allen & Smolensky, P. 1993. Optimality Theory: Constraint interaction in generative grammar. Optimality Theory in phonology.
R Core Team. 2021. R: A language and environment for statistical computing. R Foundation for Statistical Computing Vienna, Austria. https://www.R-project.org/.
Schuler, Kathryn & Yang, Charles & Newport, Elissa. 2021. Testing the tolerance principle: Children form productive rules when it is more computationally efficient. Preprint uploaded to PsyArXiv. DOI: http://doi.org/10.31234/osf.io/utgds
Shih, Stephanie S. 2017. Constraint conjunction in weighted probabilistic grammar. Phonology 34(2). 243–268. DOI: http://doi.org/10.1017/S0952675717000136
Smith, Brian W & Pater, Joe. 2020. French schwa and gradient cumulativity. Glossa: a journal of general linguistics 5(1). DOI: http://doi.org/10.5334/gjgl.583
Smolensky, Paul. 1986. Information processing in dynamical systems: Foundations of harmony theory. Tech. rep. Colorado Univ at Boulder Dept of Computer Science.
Smolensky, Paul. 1993. Harmony, markedness, and phonological activity. In Rutgers optimality workshop, vol. 1.
Sommerstein, Alan H. 1974. On phonotactically motivated rules. Journal of Linguistics 10(1). 71–94. DOI: http://doi.org/10.1017/S0022226700004011
Vasishth, Shravan & Nicenboim, Bruno & Beckman, Mary E & Li, Fangfang & Kong, Eun Jong. 2018. Bayesian data analysis in the phonetic sciences: A tutorial introduction. Journal of phonetics 71. 147–161. DOI: http://doi.org/10.1016/j.wocn.2018.07.008
Walker, Rachel. 2011. Vowel patterns in language, vol. 130. Cambridge University Press.
White, James Clifford. 2013. Bias in phonological learning: Evidence from saltation: UCLA dissertation.
Wilson, Colin. 2006. Learning phonology with substantive bias: An experimental and computational study of velar palatalization. Cognitive science 30(5). 945–982. DOI: http://doi.org/10.1207/s15516709cog0000_89
Wilson, Colin & Obdeyn, Marieke. 2009. Simplifying subsidiary theory: statistical evidence from Arabic, Muna, Shona, and Wargamay. Unpublished manuscript, Johns Hopkins University.
Wolf, Matthew & McCarthy, John J. 2010. Less than zero: Correspondence and the null output. In Blaho, Sylvia & Rice, Curt (eds.), When nothing wins: Modeling ungrammaticality in ot, 17–66. Equinox Publishing.
Yang, Shiying & Sanker, Chelsea & Priva, Uriel Cohen. 2018. The organization of lexicons: A cross-linguistic analysis of monosyllabic words. In Proceedings of the society for computation in linguistics (scil) 2018. 164–173.
Zuraw, Kie & Hayes, Bruce. 2017. Intersecting constraint families: an argument for harmonic grammar. Language 93(3). 497–548. DOI: http://doi.org/10.1353/lan.2017.0035